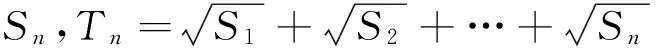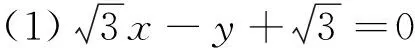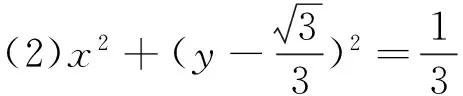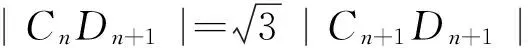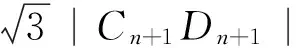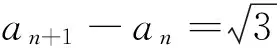对一道解几与数列交汇试题的探究
安徽省宁国中学 (242300)
陈晓明
对一道解几与数列交汇试题的探究
安徽省宁国中学(242300)
陈晓明
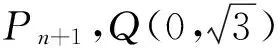
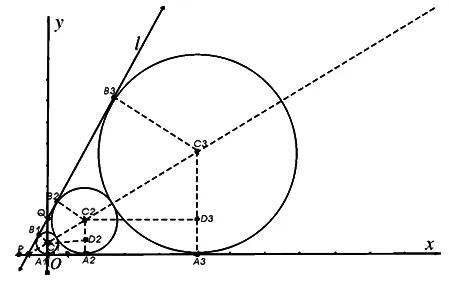
图1
(1)求直线l的方程;
(2)若a1=0,求圆C1的方程;
(3)若a1=0,求数列{an}的通项公式.
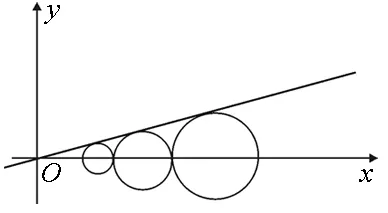
图2
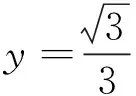
(1)证明:{rn}为等比数列;
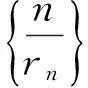
变式题再现(“江淮十校”2016届高三第一次联考数学理科压轴题)(以下简称试题3):
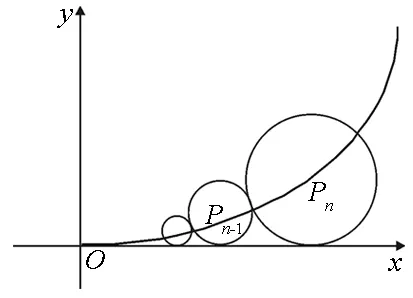
如图3,在xOy平面上有一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…对每个正整数n,点Pn位于函数y=x2(x≥0)的图像上,以点Pn为圆心的圆Pn与x轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1 图3 试题对比试题2与1,3的区别主要是圆心: (2)离原点越来越远(试题1,2)变到离原点越来越近(试题3). 试题1解法探究 解法1反思:(1)通性通法,朴素自然,由三个条件得三个结论,联立得解,一目了然;(2)考查了直线与圆,圆与圆相切的性质,点到直线的距离公式,线性规划,由数列递推公式求通项公式的方法;(3)考查了消元的思想,转化与化归的能力. 解法2反思:(1)运用了角平分线定理的逆定理对条件进行了转化,化复杂为简单,巧妙!与解法1可谓异曲同工;(2)灵活运用直线斜率与倾斜角的关系,从而引入直线的点斜式方程,渗透了方程思想;(3)由数列的递推公式转化为等比数列来求通项公式,抓住了问题本质. 解法3:如图1,过点Cn向Cn+1An+1作垂线CnDn+1,垂足为Dn+1.易知∠Cn+1CnDn+1=30°. 解法4反思:巧妙避开了累加法,充分利用解三角形知识,简单易行! 解法小结及启示通过上述解法可看出,试题1对解几与数列中的诸多知识点都有考查,覆盖面可谓“超广”!是一个解几与数列交汇的典范! 正如著名数学教育家波利亚所说:“一个专心的认真备课的老师能够拿出一个有意义的但又不太复杂的题目,去帮助学生挖掘问题的各个方面,使得通过这道题,就像通过一道门户,把学生引入一个完整的理论领域”.[2] 陶哲轩在《解题· 成长·快乐》序言中引用古希腊哲学家普罗克洛斯的话:“这,就是数学:她提醒你灵魂有不可见的形态;她赋予自己的发现以生命;她涤尽我们有生以来的蒙昧与无知……”[3]. [1]陈晓明.对一道数列题的追根溯源及拓展研究[J].理科考试研究,2015(5):19. [2]于世章.挖掘课本习题价值上好复习课[J].数学通报,2014(12):36. [3]张晓东.说题与数学青年教师的专业成长[J].中学数学教学参考,2015(3):67.