习题教学应提升学生的思维能力——以《基本不等式》习题课为例

浙江安吉孝丰高级中学　(313300)

张忠潮　汪本旺



习题教学应提升学生的思维能力
——以《基本不等式》习题课为例

浙江安吉孝丰高级中学(313300)

张忠潮汪本旺

习题课是高中数学最为常见的课型，数学学科的特性决定了习题教学的重要性，其直接影响着数学教学的整体教学质量.通过习题课的教学，学生能够加深对基础知识的理解，提升应用能力，培养逻辑思维和解决问题的能力.那么如何通过习题课去提高学生的思维能力呢？本文以《基本不等式》习题课为例，谈谈怎样由习题去提升学生的解题思维能力.

一、注重小题训练，构建学生的知识体系

高中数学给人的感觉就是“题海战术”，学生做了大量的题目，但对数学知识的发生、发展、结构并没有很好的认识，而数学知识在难度和广度上是呈螺旋式形态上升的，因此数学知识积累到一定程度时，要让学生在原有知识结构的基础上借助思维导图从整体角度审视这些知识，整合新旧知识间的知识体系，从而达到融会贯通的目的[1].

教学片段一

让学生课前预习并梳理基础知识后完成：

1．已知m>0，n>0，且mn=81，则m+n的最小值为().

A．18B．36C．81D．243.

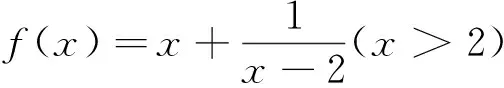
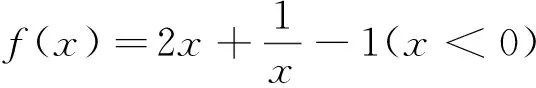
A.有最大值B.有最小值

C.是增函数D.是减函数.

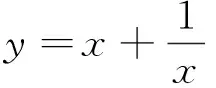
反思：这五个小题训练呈现出本节课的教学内容，学生完成这五个小题训练后，在组内成员间进行充分讨论后，对学习的内容进行梳理，借助于思维导图找出知识点的相互关系，同时表达自己对所学内容的认识和理解.

二、注重试误训练，培养学生思维严谨性

很多数学老师都有这样的感觉：题还是那道题，错误还是同样的错误，为什么讲了那么多遍，学生还是会犯同样的错误.在抱怨之后，我们是否应该认真的反思呢？我们平时的数学教学，特别是习题教学，是否有点急躁了，刚刚讲完一题，就马不停蹄的去解下一题，生怕实践不够，课堂教学目标完成不了.同时在错误分析中，我们总是第一时间给出自己想要的正确解法，是否真正了解学生的错误根源所在，真正的聆听了学生的想法，真正对症下药呢？因此，笔者认为在习题课上，试误训练[2]，就显得尤为重要.

教学片段二

甲、乙、丙、丁位同学分别给出了他们的各自的解法，哪位同学的解法正确？为什么？

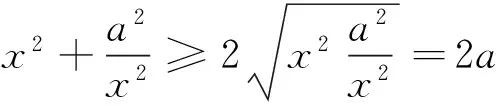
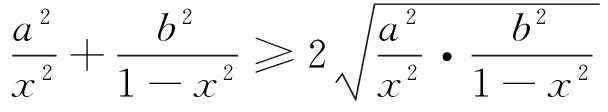
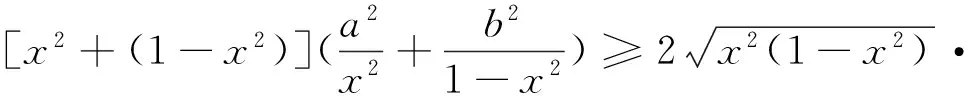
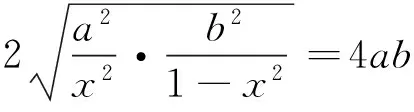
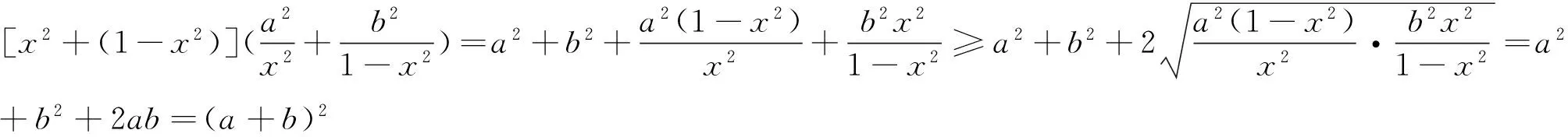
共同析错：要求同学们思考、讨论四位同学的解法是否正确，如果错误，如何改正？

反思：设置试误训练，就是要帮助学生反思错误的根源，找到错误原因，就是要站在学生的角度，沿着学生的思路来解释疑惑，而不是撇开学生的想法，硬把“教师觉得最好的解法”灌输给学生，只有这样换位思考，才能让学生理解的更加深刻.

三、注重方法优化，培养学生的解题策略

一题多解是高中数学习题课最常用的教学方式，文[3]认为一题多解要“见机行事”，文[4]认为不是每种方法都要讲，但通性通法要重点讲.而多数高考题都有一个显著特征：求解入手较宽，方法往往呈现多样化，不同方法的选择将会产生不同的解题效果，从而有效区分出学生的不同水平.我们都希望学生能在高考时用相对较好的方法解决问题，这就需要在平时养成优化解法的习惯，特别是在习题课讲评上.

教学片段三

解题教学不能得到答案就了事，还要多问为什么，比如题意都明白吗？你有哪些想法？你是怎么想到的？还有其他想法吗？等等，在这些问题的启发下，就有学生反思解法，可能会发现更简捷的求解方法.

比如学生2提供了他的解法(巧用“1”)，如下：

对于条件是线性的二元关系时，一些学生发现了优化上述解法的途径，采用通法去解决此类问题，比如学生3提供了他的解法(消元法)，如下：

反思：数学习题教学中，教师如果过于强调一题多解，学生听起来感觉像是欣赏魔术，当时可能觉得很神奇，但是知识运用相对较窄，影响也相对较小，并且还会很快忘记.此时不妨突出解决问题的通法通性，它是以基础知识为依据，是在多种解法中发现更加优化的解题方法.

四、注重变式训练，提升学生的思维品质

同样的题目，有人拿到手就急于入手，有的人则冷静地观察题目的特点：题目的条件和结论分别是什么？他们之间有什么关系？这个问题用到什么知识？是解决什么样的一个问题？这个问题以前有类似的背景吗？能找到更加简单的方法吗？等等，通过分析形成问题的逻辑思维结构，根据自身的知识认知？确定问题的方案，试图找出问题的关系，进一步提升学生的思维品质.

教学片段四

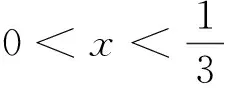
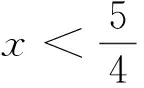
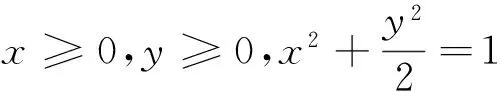
这里学生尽管找到了题目的答案，但是学生能否感受到它们之间的联系和本质差别？是否有统一的解法呢？等等，这些就需要教师在习题教学中逐步去引导学生思考，发现它们之间关联所在，从而提高学生的认知精度.

总之，在习题教学中，让学生有针对性的解决问题，这有利于学生对数学知识的理解和掌握，引导学生通过习题的讲解去构建知识体系，培养学生思维严密性，优化解题策略，最终达到帮助学生把握数学本质，提升学生的思维能力.

[1]祝要辉．反思中提升学生的思维能力[J].数学通讯，2015(10)：18-21.

[2]张荣欣.浅谈如何提高高中数学习题课教学效率[J].高中数理化，2015(2)：11-12.

[3]吕增锋.一题多解要见机行事[J].中学数学教学参考(上旬), 2012(1-2)：22-23.

[4]缪荷芳.一节高三“一题多解”课的听后感[J].中学数学教学参考(上旬), 2012(1-2)：24-26.