结构性软土粘弹塑性边界面损伤本构模型

温欣 ，徐东强，闫文赏，张媛

(1.河北工业大学 土木工程学院，天津 300130；2.唐山工业职业技术学院 建筑化工系，河北 唐山 063200；3.华北理工大学 建筑工程学院，河北 唐山 063000)



结构性软土粘弹塑性边界面损伤本构模型

温欣1,2，徐东强1，闫文赏3，张媛2

(1.河北工业大学 土木工程学院，天津 300130；2.唐山工业职业技术学院 建筑化工系，河北 唐山 063200；3.华北理工大学 建筑工程学院，河北 唐山 063000)

各向异性；边界面模型；损伤；粘弹塑性

在软土流变性的滞后流变理论基础上，引入考虑损伤和各向异性影响的边界面理论，建立结构性软土粘弹塑性边界面损伤本构模型，并将软土的粘弹塑性边界面损伤模型计算结果与常规室内三轴蠕变试验数据进行比较分析。结果表明：对应不同偏应力比，围压较高时的轴应力-时间曲线和孔隙水压力-时间曲线蠕变特征明显，围压较低条件计算曲线略低于对应试验数据，表明初始作用阶段模型参数设定、土样的试验误差等因素误差导致土样初始变化具有复杂性，但总体计算模型同试验数据基本吻合，表明模型分析的有效性。

在我国沿海地区分布着结构性和流变性特征明显的天然软土，大量工程实践表明，充分理解软土结构特性对于软土地区地基、路基的变形预测与沉降控制具有重要影响，必须加以重视。魏星、黄茂松[1]在边界面模型的基础上引入各向异性张量，建立了各向异性的边界面和硬化法则；为了考虑软土的破损过程，孙吉主、王勇等[2]在边界面理论的弹塑性模量中引入损伤函数，建立了结构性软土的边界面损伤模型；区别于传统的Perzyna流变理论，为了更方便地描述软土流变性，Dafalias[3]进一步提出了基于滞后变形理论的弹塑性-粘塑性理论；李兴照、黄茂松等[4]将准前期固结压力引入边界面理论，提出了流变性软粘土的粘弹塑性边界面损伤本构模型。

现有流变模型研究成果多是通过完善已有模型缺陷，进而建立新的流变本构模型。该项研究通过基于修正的剑桥模型的边界面理论，符合软土性状的假设以及岩土损伤理论首先构建了边界面损伤方程，并作为滞后变形理论中的软土塑性应变基本方程体现软土的结构性特征，为了保证滞后粘性应变求解的概念简单、参数意义明确，粘性应变包括的体积蠕变和剪切蠕变分别按照对应蠕变规律求解，在体现软土结构性、流变性优点基础上，提出一个适用于工程实践的粘弹塑性边界面损伤本构模型，对沿海软土长期蠕变沉降进行预测和控制。

1 边界面损伤方程构建

1.1边界面方程构建

边界面理论适用于结构性土体和流变性土体，天然粘土的结构性和各向异性是互相影响的，二者都会影响土体塑性变形的发展，为便于研究，该项研究边界面模型做出如下假定：(1)土体结构性的形成只与颗粒间的胶结强度相关，与颗粒排列无关；(2)应力状态落在边界面内部或边界面上；(3)边界面大小由硬化规律决定；(4)弹性应变由广义虎克定律计算；(5)假设应力作用导致结构性各向异性的改变只与颗粒排列有关，可以通过倾斜边界面的方法表征软土的初始各向异性；(6)边界面上的应力点塑性应变增量大小由流动法则确定；(7)土体在边界面内部也能产生塑性应变，塑性模量大小依赖于映射规律，也即由当前应力点与其在边界面上的对应像应力点之间的距离确定；(8)本模型不考虑纯弹性区域，采用类似修正剑桥模型的椭圆屈服面作为边界面。

在p-q应力空间选取边界面为椭圆见图1，椭圆与p轴正向相交于点A (p0，0)，椭圆顶点与CSL(临界状态线，斜率为M)相交于顶点B，R为形状参数，实际应力状态(p，q)与其在边界面上的像应力符合径向投影规律，本文在修正剑桥模型的椭圆屈服面基础上引入各向异性张量和损伤变量更准确的描述土体的屈服状态，p-q空间的边界面性状见图1，结构性土边界面具体方程如(1)式：

图1　p-q应力空间边界面

(1)

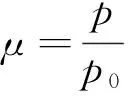
(2-a)

(2-b)

(2-c)

(2-d)

模型中涉及到的硬化内变量包括p0和aij，前者根据软土压缩性采用等向硬化法则，后者采取Wheeler各向异性硬化法则[4]。

(3)

式中： ψ、m为模型参数。

1.2损伤变量引入

正常固结天然软粘土的基本特征之一是具有结构性，且不可逆，土体刚度在加载时增加，但同时因为土体损伤会发生衰减，因此呈现出相反的变形机理，因此有必要在边界面模型中引入岩土损伤理论，定义土体损伤变量为ω。

(4)

根据Lemaitre等效应力变假设，应力作用在受损土体引起的应变与等效应力作用在无损材料上引起的应变等价，也即损伤土体的本构关系可以采用无损时的形式，因此认为损伤过程表现为土体刚度的衰减，也就是无损状态模量的逐步衰减过程，(1-dpω)作为损伤导致的“劣化因子”被结合到粘弹塑性土体中，岩土力学材料参数损伤可用下式表示[5]：

Sd=(1-dpω)Si

(5)

1.3边界面损伤方程构建

边界面模型的损伤主要体现为塑性应变塑性模量Hp的衰减，引入“劣化因子”后塑性应变损伤模量Hpd表示如下：

Hpd=(1-dpω)Hp

(6)

将式(6)代入式(1)、式(3)可得各向异性边界面损伤方程。

2 结构性软土粘弹塑性边界面损伤方程

方程建立基于Bjerrum提出的滞后变形理论，土体总应变由弹性应变εe，考虑损伤的塑性应变εpd和滞后应变εt构成，其中滞后应变εt又包括体积蠕变εtv和剪切蠕变εts

(1)弹性应变εe可不考虑损伤影响，由广义胡克定律直接求取，表述如(7)式所示[6]：

(7)

(2)塑性应变εpd考虑损伤影响，由前文考虑损伤影响边界面方程计算，表示如下：

(8)

(3)滞后应变εt由体积蠕变εtv和剪切蠕变εts构成，考虑到结构性软土蠕变的非线性特征，采用Taylor次固结理论计算体积蠕变εtv，采用Singh-Mitchell剪切蠕变公式计算剪切蠕变εts[7]。

体积蠕变率不考虑初始应变的积分变化形式为：

(9)

剪切蠕变率采用积分变化后，m≠1且不考虑初始应变的Singh-Mitchell剪切蠕变公式

(10)

(11)

3 模型特性与预测分析

唐山沿海软土虽然按照土质分类为淤泥，但唐山沿海地基处理工程涉及的原状土室内、室外试验结果表明其具有一定的抗剪强度，呈现典型的结构性，为了验证本文所提出模型的合理性，运用前面建立的考虑边界面损伤的粘弹塑性流变模型对该海域原状灰色淤泥质软土进行蠕变过程进行计算，通过常规室内实测土样的三轴蠕变不排水轴向应变和孔隙水压力试验，并将不同围压(σ3=100kPa，σ3=200kPa)、不同偏应力比(n=0.2，n=0.4)的实测土样试验结果同模型计算结果进行比较分析，土样的主要物理力学指标见表1，模型参数依据可拟合曲线及经验确定，合理的取值可提高模型计算的精度，具体选用见表2所示，与试验数据比较结果如图2,图3所示，其中曲线代表理论计算结果，点符代表试验数据。

表1　土样的主要物理力学性质

表2　粘弹塑性流变模型计算参数

图2　不同偏应力比轴向变形-时间试验同计算比较

图3　不同偏应力比孔隙水压力-时间试验同计算比较

从图2、图3结果对比可以看出，不同条件下模型计算结果同试验数据发展规律基本吻合，不同偏应力比(n=0.2，n=0.4)条件下，高围压(σ3=200kPa)状态轴应力-时间和孔隙水压力-时间曲线蠕变趋向稳定，低围压(σ3=100kPa)状态上述曲线的初始阶段模拟计算值要小于试验观测数据，可能因素在于土体取样时扰动影响导致以及模型初始条件设定和模型参数取值同土样实际性能参数存在一定差异，需要对模型尽可能引入初始条件，并对模型参数进行合理性调整。

4 结论

(1)提出了考虑各向异性边界面损伤的粘弹塑性软土本构模型，分析假定贴近土体原始性状，在保留了经典边界面塑性模型的各种功能基础上引入了各向异性张量。

(2)提出的分析模型涉及损伤因素在分析中直接体现为边界面塑性模量的衰减，容易理解，计算方便。

(3)模型分析中通过对边界面理论、损伤理论、滞后变形理论的合理引入，将淤泥质软土各种特性进行耦合分析，模型计算结果同室内土工三轴试验数据基本吻合，误差较小，该模型建模思路清晰，模型的物理意义明确，易于被岩土工作者接受。

[1]魏星,黄茂松. 粘土的各向异性边界面模型[J] .水利学报,2006,37(7):831-837.

[2]孙吉主,王勇,孔令伟.湛江海域结构性软土的边界面损伤模型研究[J].岩土力学,2006,27(1):99-101.

[3]DAFALIAS Y F. Bounding surface elastoplasticity viscoplasticity for particulate cohesive media[C]. //LUGER H J ed. Proceedingly of IUTAM Symposium on Deformation and Failure of Granular Materials. Rotterdam：A. A. Balkema,1982:97-107.

[4]李兴照,黄茂松,王录民. 流变性软粘土的弹粘塑性边界面本构模型[J] .岩石力学与工程学报,2007，26(7):1393-1401.

[5]柳艳华,黄茂松,李帅. 循环荷载下结构性软粘土的各向异性边界面模型[J] .岩土工程学报, 2010，(7): 1065-1071.

[6]Wheeler S, Naatanen A, Karstunen M. Anisotropy hardening model for normally consolidated soft clays[A]. Proc. of NUMOG VII[C]. Graz,1999.

[7]陈晓平,白世伟. 软粘土地基粘弹塑性比奥固结的数值分析[J] .岩土工程学报, 2001,23(4):481-484.

[8]沈珠江. 理论土力学[M]. 北京:中国水利水电出版社, 2000:60-66.

[9]潘晓明,杨钊,雷春娟,等. 广义西原粘弹塑性流变模型在ABAQUS中开发与应用[J].建筑结构学报(S2),2010，(S2):324-329.

[10]熊传祥. 软土结构性与软土地基损伤数值模拟[D]. 浙江大学,2000.

Constitutive Model of Visco-elasticity Plasticity Boundary Surface Damage of Structural Soft Soil

WEN Xin1,2, XU Dong-jiang1, YAN Wen-shang3, ZHANG Yuan2

(1.Institute of Civil Engineering，Hebei University of Technology, Tianjin 300130, China；2. Department of Architecture and Chemical Engineering, Tangshan Industrial Vocational and Technical College, Tangshan Hebei 063200, China；3. College of Civil and Architectural Engineering, North China University of Science and Technology, Tangshan Hebei 063000, China)

anisotropy;boundary surface model;damage;visco-elasticity plasticity

On the basis of lagging rheological theory of soft soil rheological property,the theory of anisotropic boundary surface theory considering the effects of injury is introduced in setting up constitutive model of visco-elastic plastic boundary surface damage for structural soft soil and the model calculation results of soft soil is compared with indoor triaxial creep test data. The results of the comparison indicate: in corresponding to different deviatoric stress ratio and under the higher confining pressure the characteristics of curve about the axial stress - time curve is obvious, as well as the pore water pressure and time curve, corresponding to the test data, the calculated curve is lower than the test data under low confining pressure conditions，which shows the initial change soil sample may be complex due to model parameter setting，soil sample test error and so on，but the overall calculation model is consistent with the test data，which proves the effectiveness of the model analysis.

2095-2716(2016)03-0114-06

TU431

A