《一次函数》测试题
谢林
一、选择题(每小题3分,共21分)
1.若正比例函数的图象经过点(-1,2),则这个图象也必经过点( )。
A.(1,2) B.(-1,-2)
C.(2,-1) D.(1,-2)
2-若一次函数y=kx+b的函数值y随着x的增大而减小,且其图象与y轴的正半轴相交,那么对k和b的符号判断正确的是( )。
A.k>0,b>0 B.h>0,b<0
C.k<0,b>0 D.k<0,b<0
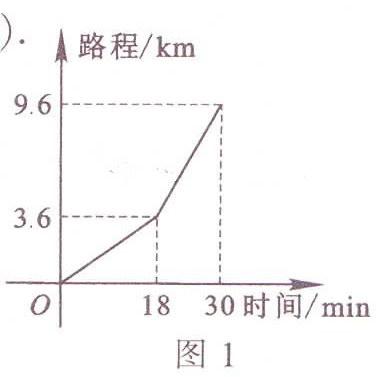
*3。小明早晨从家骑车到学校。先上坡后下坡,行程情况如图1所示。若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家所用的时间是( )。
A.37.2min
B.48min
C.30min
D.33min
4.将直线y=2x向上平移2个单位长度所得的直线的解析式是( )。
A.y=2x+2 B.y=2x-2
C.y=2(x-2) D.y=2(x+2)
*5.某市储运部紧急调拨一批物资。调进物资共用4 h。调进物资2 h后开始调出物资(调进物资与调出物资的速度均保持不变)。储运部库存物资量S(t)与时间t(h)之间的函数关系如图2所示。这批物资从开始调进到全部调出需要的时间是( )。
A.4 h B.4。4 h
C.4.8 h D.5 h
*6.已知整数x满足-5≤x≤5。设y1=x+1,y2=-2x+4。对任意一个x,取y1,y2中的较小值作为m。则m的最大值是( )。
A.1 B.2 C.24 D.-9
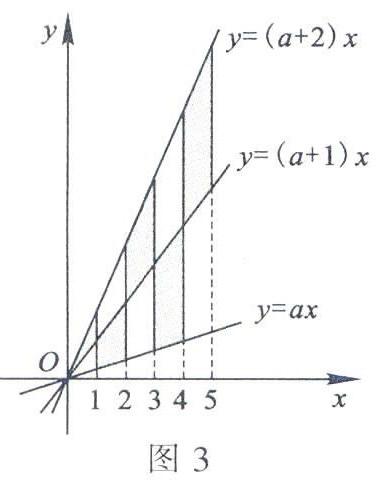
*7.如图3,在x轴上有五个点,它们的横坐标依次为1,2,3,4,5。分别过这些点作x轴的垂线。与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0,则图中阴影部分的面积是( )。
A.12.5 B.25
C.12.5a
D.25a
二、填空题(每小题3分,共15分)
8.若一次函数y=3x+b2的图象过点(1,4),则b的值为____。
9.某书每本定价8元。若购书不超过10本,按原价付款;若一次购书10本以上,超过10本的部分打8折。设一次购书数量为x本,付款金额为y元,请填写下表:
10.直线y=kx+b经过点4(-2,0)和y轴上的一点B。如果△ABO(O为坐标原点)的面积为2,则b的值为____。
*11.正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图4所示的方式放置。点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上。已知点B1(1,1),B2(3,2),则点Bn(n为正整数)的坐标是____。
12.如图5,一束光线从y轴上点A(0,1)处发出,经过x轴上的点B反射后。又经过点C(6,2)。则光线从A点到C点经过的路线的长为____。
三、解答题(共64分)
13.(8分)已知y与z成正比例,且x=2时,y=-6。
(1)求y与x的函数关系式。
(2)当x=4时,求y的值。
(3)当y>3时,求自变量x的取值范围。
14。(8分)已知一次函数的图象过M(1,3),N(-2,12)两点。
(1)求函数的解析式。
(2)试判断点P(2a,-6a+8)是否在这个函数的图象上。并说明理由。
15.(12分)在平面直角坐标系中,点A的坐标为(4,0)。点P在直线y=-x-m上,且AP=OP=4。则m的值是多少?
*16.(12分)某服装店欲订购甲、乙两种新款运动服,甲款每套进价350元,乙款每套进价200元。该店计划用不低于7 600元且不高于8000元的资金订购甲、乙两款运动服共30套。