改进的自适应噪声总体集合经验模态分解在光谱信号去噪中的应用

李晓莉，李成伟

(哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001)



改进的自适应噪声总体集合经验模态分解在光谱信号去噪中的应用

李晓莉，李成伟*

(哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001)

针对近红外无创血糖检测过程中噪声对血糖浓度模型精度和稳定性的影响，提出用自适应噪声总体集合经验模态分解方法实现近红外光谱信号的去噪；同时，根据原始信号曲率和分解后本征模态函数(IMFs)曲率间的离散弗雷歇距离选择相关模态。首先，将自适应噪声的总体集合经验模态分解方法引入近红外光谱去噪过程，介绍了经验模态分解、集合经验模态分解、互补集合经验模态分解及自适应噪声总体集合经验模态分解的基本原理及具体实现过程。然后，应用基于曲率和离散弗雷歇距离的自适应噪声总体集合经验模态分解改进算法对仿真信号和光谱信号进行去噪，并将其标准差和信噪比作为评价指标。实验结果表明：应用提出的方法得到的血糖浓度近红外光谱数据其标准差为0.179 4，信噪比为19.117 5 dB，实现了信号与噪声的分离，改善了重构信号质量，具有良好的自适应性，可以有效识别并提取有用信息。

无创血糖检测；近红外光谱；信号去噪；自适应噪声总体集合经验模态分解；曲率；离散弗雷歇距离

1　引　言

糖尿病是威胁人类健康的重大疾病之一，而且糖尿病患者的数量正以惊人的速度增长，目前，世界上已经有超过一亿的人患有糖尿病，预计到2030年将增加到3亿。糖尿病患者虽然可以通过调整饮食或是注射胰岛素来调节血糖水平，但糖尿病后期会引起严重的并发症，例如：心脏衰竭和失明。所以，糖尿病的预防非常重要，无创血糖检测方法由于可以减少频繁检测所带来的疼痛感并降低医疗成本，故得到广泛应用。无创血糖检测技术包括吸收光谱法、光声光谱法、光偏振法、荧光法和介电光谱法[1-3]。Arlen Duncan等在1995年利用脉冲光声光谱法检测手指血液内的葡萄糖浓度[2]。J.R. Blanco等在2006年研制出一种便携式葡萄糖传感器，该设备通过测量特定物质和生物识别系统之间电子交换产生的电流检测葡萄糖浓度[3]。2011年，Ashok等利用反式激光束测量糖尿病患者的血糖浓度[4]。基于近红外光谱进行无创血糖检测已经成为国内外专家学者的研究热点[1]。

在近红外光谱测量中，噪声是一个重大的挑战。目前存在的去噪方法主要有基于模型方法、变换域方法和自适应滤波方法[5-7]。维纳滤波器由于具有易于实现和设计的优点，已经被广泛应用，但是这种线性方法只能用于稳定信号。为了克服这个限制，有学者提出了基于小波阈值的非线性方法。然而小波方法的基函数是固定的，不能对所有的真实信号都匹配。准确地说，这种局限性源于它的非自适应性，一旦确定好基小波，它将被用于分析所有数据，如果选择的小波分解不合适将会限制其去噪性能。经验模态分解(Empirical Mode Decomposition， EMD)常被用于分析非稳态和非线性数据[8-9]，它可以将任意信号分解成不同的振荡成分，即本征模态函数(Intrinsic Mode Functions， IMFs)。这个强大的自适应工具非常适合解决测量领域中的噪声和频率估计问题，但EMD是基于相关模态的局部重建，用其进行信号滤波属于自适应方法，故周期性信号引起模态混叠的问题。集合经验模态分解(Ensemble Empirical Mode Decomposition， EEMD)可有效地解决这个问题，但同时也引入了新的问题，即在重构信号中含有残留噪声。目前，EMD和EEMD两种方法已经广泛应用于各个领域[10-14]。互补集合经验模态分解(Complementary Ensemble Empirical Mode Decomposition， CEEMD)可以抑制重构余项并消除IMF里的残余噪声，但是当参数选择不当时，会产生错误成分导致最后获得的IMF不能真正满足IMF的定义。为了克服这个问题，本文提出了自适应噪声的总体集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise， CEEMDAN)算法来获得准确的原始信号重构和纯净的分解模态光谱。

2　EMD方法及其改进版本

2.1EMD方法

EMD通常将信号分解为小数量的IMFs，IMF应该满足以下2个条件：(1)极值点和过零点的数量相等或最多相差一个点。(2)任一点的上下包络线均值需为零[15]。EMD是一种通过连续减去包络均值去除震荡的自适应方法。对于信号x(t) 而言，EMD算法包括以下步骤[16]：

(1)利用三次样条插值法顺序连接局部最大值(最小值)点，获得上(下)包络线。

(2)定义上下包络线的均值m(t)。

(3)提取瞬时局部振荡h(t)=x(t)-m(t) 值。

(4)重复步骤(1)～(3)，直到m(t)接近于零，则h(t)是一个IMF，记为c(t)。

(5)计算余项r(t)=x(t)-c(t)。

(6)余项r(t)作为x(t)，重复步骤(1)～(5)产生下一个IMF和余项，直到余项成为单调函数。

因此，原始信号x(t)可以重构为：

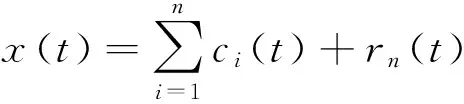
(1)

式中：ci(t)为第i个IMF；rn(t)为第n个余项。

2.2EEMD方法

由于EMD算法是利用局部极值构建包络线的，信号的中断会引起模态混叠，因此学者们提出了EEMD算法以解决此问题。EEMD算法[15]描述如下：

(1)令xi(n)=x(n)+wi(n)，式中wi(n)(i=1，…，l)为不同的高斯白噪声。

2.3CEEMD方法

在CEEMD算法中，在原始信号中加入成对的白噪声产生两个IMFs集合，因此可以推出两个信号和白噪声组合的混合集合[16]：

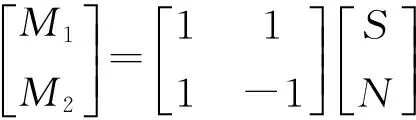
(2)

其中：S是原始数据；N是添加的白噪声；M1是原始数据和正噪声的和；M2是原始数据和负噪声的和。最终的IMF是IMFs和正负噪声的集合。由于成对的噪声可以有效消除最终白噪声余项，因此CEEMD可以节省计算时间。

2.4CEEMDAN方法

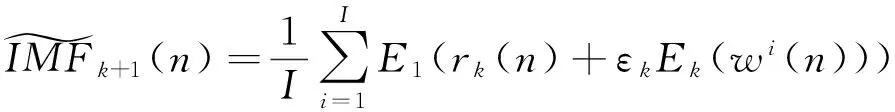
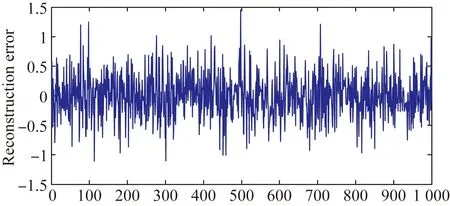
为了比较EMD、EEMD、CEEMD和CEEMDAN 4种方法的分解效果，将理想心电(ECG)信号加上5 dB噪声作为仿真信号，如图1所示。利用上述4种方法进行分解，图2和表1分别给出了4种方法分解后的重构误差和标准差值，由仿真实验可知，EMD和CEEMDAN的重构误差及标准差值要小于EEMD和CEEMD，但是由于EMD方法具有模态混叠的缺点，因此CEEMDAN方法更适合于非稳定信号的分解。

图1　ECG信号波形

(a)EMD

(b)EEMD

(c)CEEMD

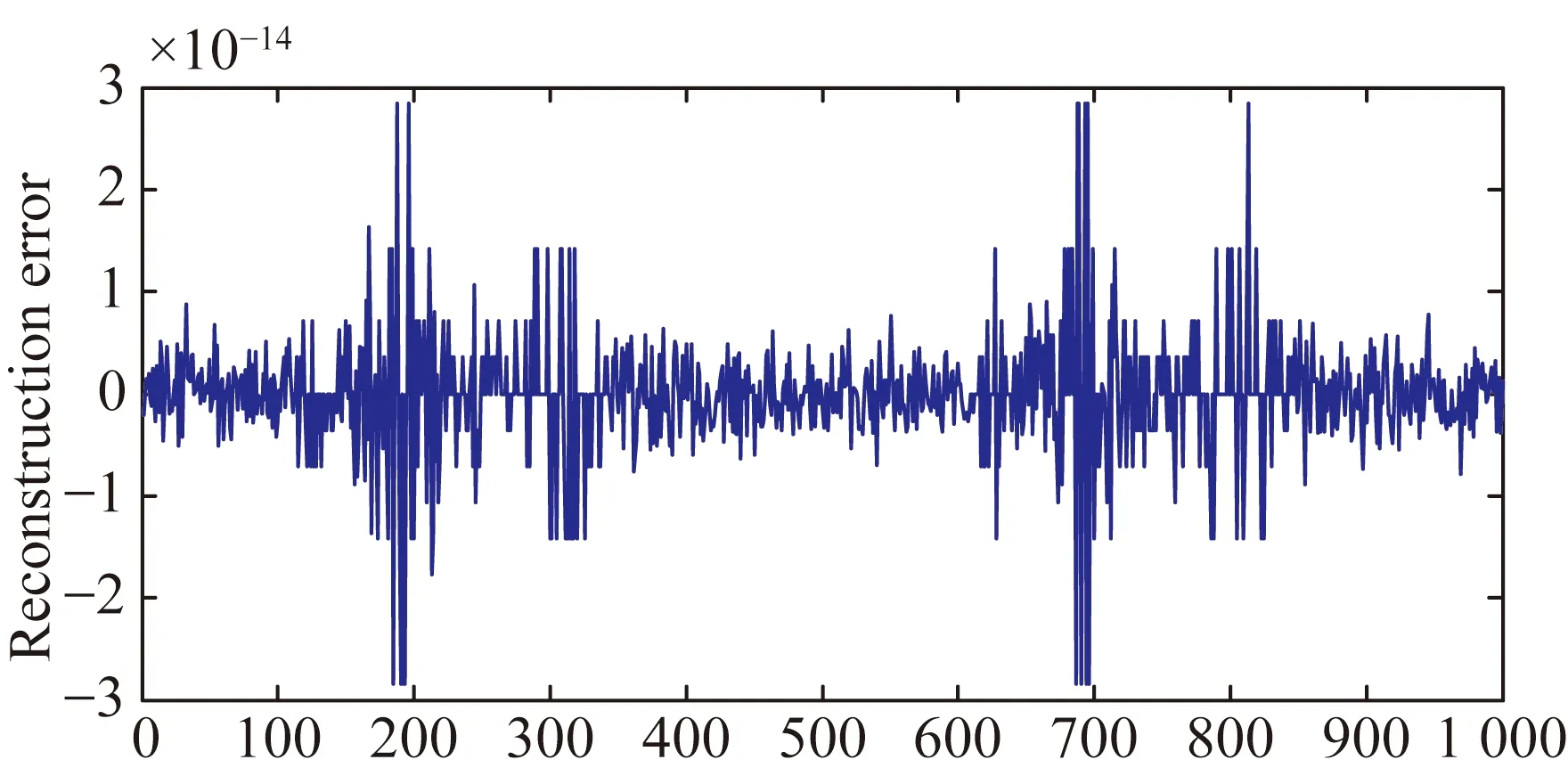
(d)CEEMDAN

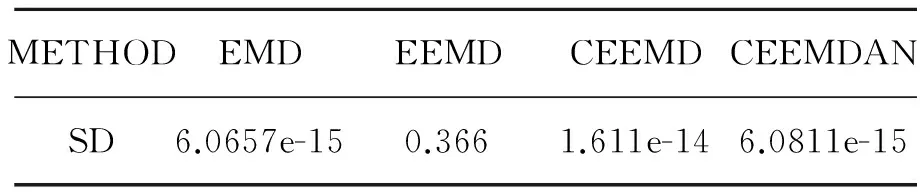
METHODEMDEEMDCEEMDCEEMDANSD6.0657e-150.3661.611e-146.0811e-15

3　改进的CEEMDAN方法

3.1曲线的曲率

曲率是指在一条曲线或不同曲线上不同点的弯曲程度[18]。每条曲线的曲率不同，曲率本身是曲率半径的倒数。对于一般的函数情况，y=f(x)，曲率k为：

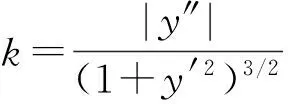
(3)

对于一条给定的曲线f(t)=(x(t)，y(t))，曲率k为：

(4)

根据实验结果可知，曲率可以准确揭示不同频率曲线的波峰或波谷的属性和位置(如图3所示)。另外，每个曲线都有其独有的曲率。因此，利用EMD方法及其改进方法分解后的模态可以看作是具有不同频率的不同曲线，即每个IMF的曲率不同。进而可以利用曲率展示不同模态的内在属性，并用于相关模态选择。

(b)信号曲率(b)Curvature of signal

3.2离散弗雷歇距离

弗雷歇距离(Frechet Distance， FD)利用两个目标的路径以及两条曲线上所有离散点的距离，测量两条曲线的相似度。弗雷歇距离最著名的一个例子是一个人和一个狗之间由一条狗绳连接，各自沿着两个路径行走，假设人和狗可以以不同的速度行走，但是不可以向后行走，弗雷歇距离就是人和狗从起点走向终点的相应路径中狗绳的最短长度。这种测量方法直观，而且与豪斯多夫距离等其他相似度测量方法相比，其可以更好地代表折线曲线的相似度。长度分别为m和n的折线曲线P和Q之间的弗雷歇距离可定义为[19]：

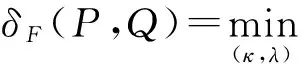
(5)

式中：Ψm,n=M([1:m+n],[0:m])×M([1:m+n]，[0:n])，[a:b]={a,a+1,…,b}，对于任何两个整数a,ba≤b。

3.3模态选择方法

对于原始信号y(t)=x(t)+n(t)，x(t)为有用信号，n(t)为噪声信号。测量信号y(t)可以被分解为n个模态(IMF1，IMF2，…，IMFn)和一个余项，所有的模态按照频率从高到低排列。一般而言，噪声存在于前几个IMFs中，纯净信号存在于后几个IMFs中，因此在噪声信号和有用信号之间会存在一个临界模态将信号分解为：

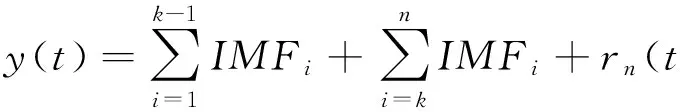
(6)

本文中所提改进方法的主要思想是找出可以区分噪声信号模态和纯净信号模态的相关模态序号K。由于所有的模态都有其固有的特性，所以每个模态的曲率曲线均不相同。模态的曲率可以记为C_IMFs，信号可以分解为

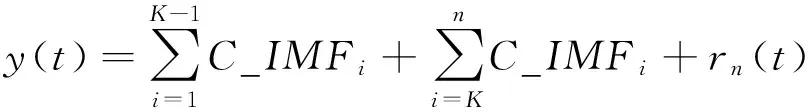
(7)

式中：C_IMFi是每个模态的曲率，n是模态的数量。有用信号的C_IMFs曲线波形与原始信号的C_IMFs曲线波形相似，与此相反，噪声信号的C_IMFs 曲线波形与原始信号的C_IMFs曲线波形不同。因此，可以用曲线波形的突变来区分噪声模态和信号模态，此时K值的求取很关键。通过计算各个C_IMFs与原始信号曲率曲线的离散弗雷歇距离可以获得K值。具体步骤如下：

(1)利用EMD、EEMD、CEEMD和CEEMDAN 4种方法分解原始信号，获得一系列IMFs。

(2)计算原始信号和所有模态的曲率，获得C_IMFs。

(3)计算原始信号曲率和每个C_IMFs之间的离散弗雷歇距离，获得FDs。

FDj={CIMF0，CIMFj}(j=1，…，n)，

(8)

式中CIMF0为原始信号y(t)曲率。

(4)相关模态序号K值由FDj确定：

K=argmin{FDj}.

(9)

(5)原始信号重构为：

(10)

3.4算法应用

将改进算法应用于真实信号y(t)，y(t)为由两个不同频率组成的周期信号，

y(t)=cos(2πf1t)+sin(2πf2t)，

(11)

式中：f1=4 Hz，f2=6 Hz，数据长度为1 024，在信号中加入信噪比为5 dB的高斯白噪声(如图4所示)。根据信号y(t)可知，第7个和第8个模态为有用信号模态(如图5所示)。不同模态的曲率曲线如图6所示，通过求取每个C_IMF与原始信号曲率曲线的离散弗雷歇距离可以获得K值(如图7所示)。纯净信号和去噪后的重构信号如图8所示(彩图见期刊电子版)。

图4　原始信号波形

图5　IMFs波形

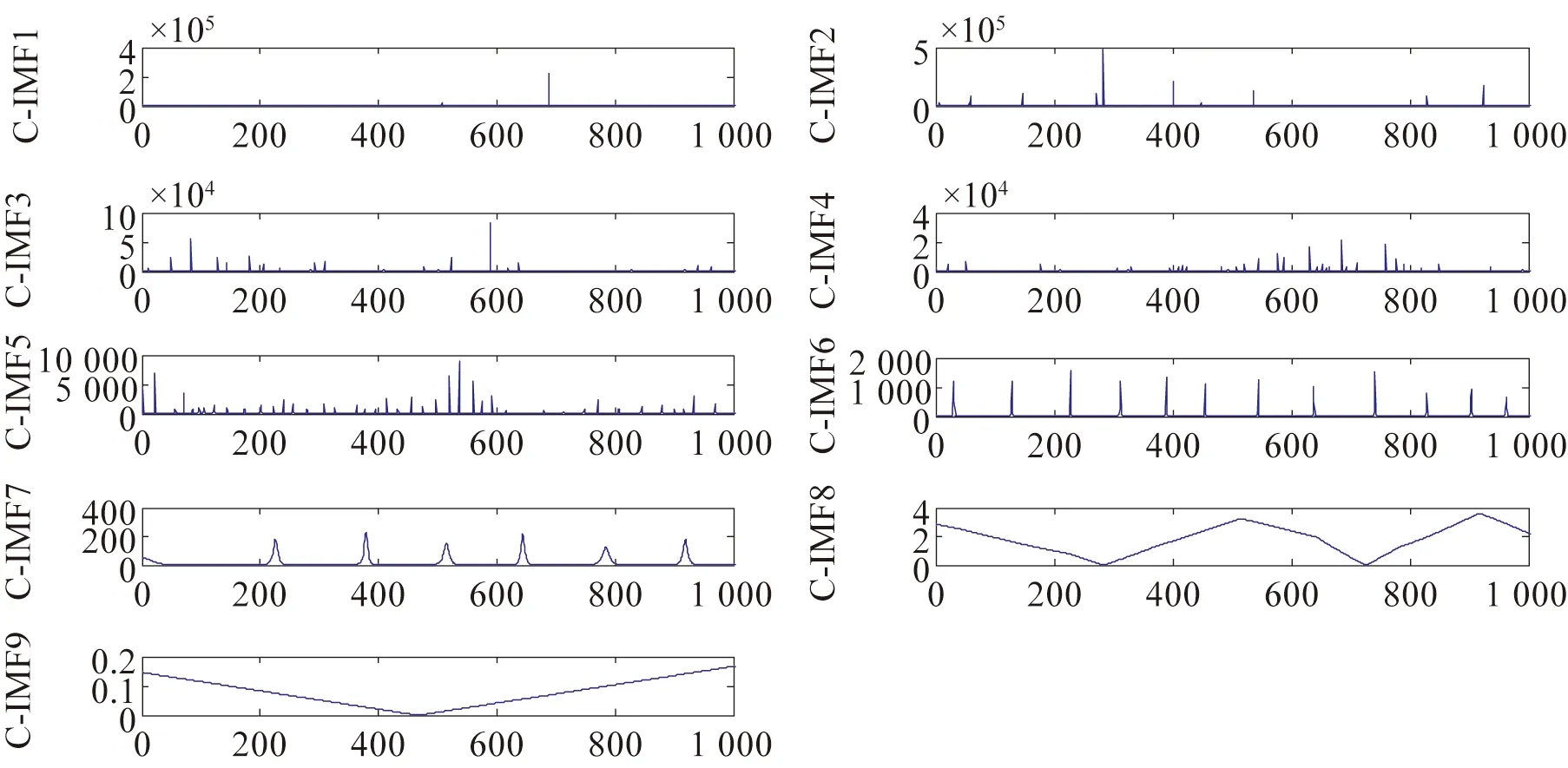
图6　C_IMFs波形

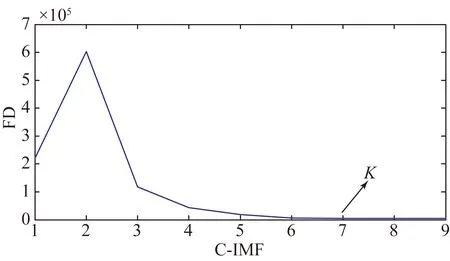
图7　C_IMFs的离散弗雷歇距离

图8　去噪后重构信号和纯净信号

4　结果与讨论

4.1仿真信号实验结果

对信号y(t)去噪后进行重构处理，对比EMD-CURVATURE-FD， EEMD-CURVATURE-FD， CEEMD-CURVATURE-FD，CEEMDAN-CURVATURE-FD 4种方法的结果(如图9所示彩图见期刊电子版)。输入信噪比(SNFin)为-15～15 dB，间隔为3 dB。输出信噪比的定义为：

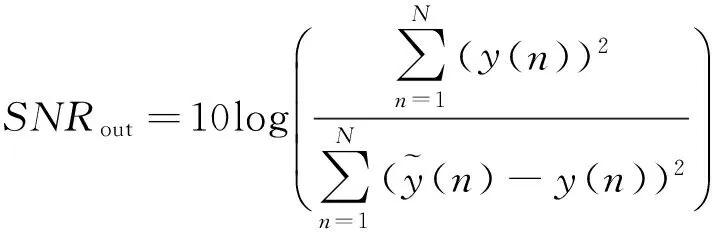
(12)

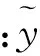
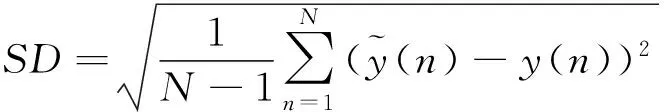
(13)

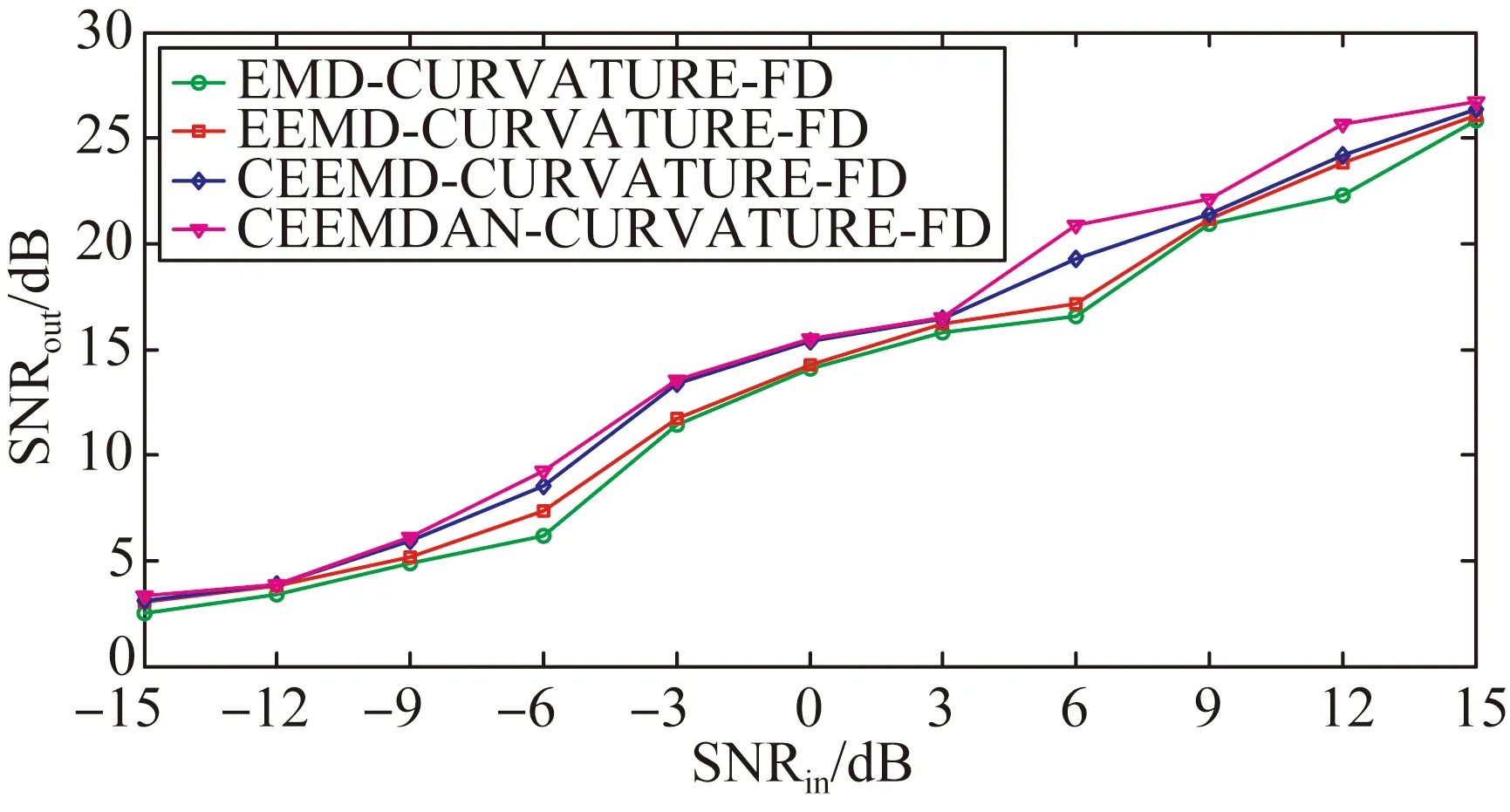
图9　4种方法输出信噪比对比结果

表2表明，所提出的基于CEEMDAN的改进算法的SD值最小，即重构误差最小。结合SNR的对比结果可知CEEMDAN-CURVATURE-FD方法在信号去噪及重构中具有较强的鲁棒性。

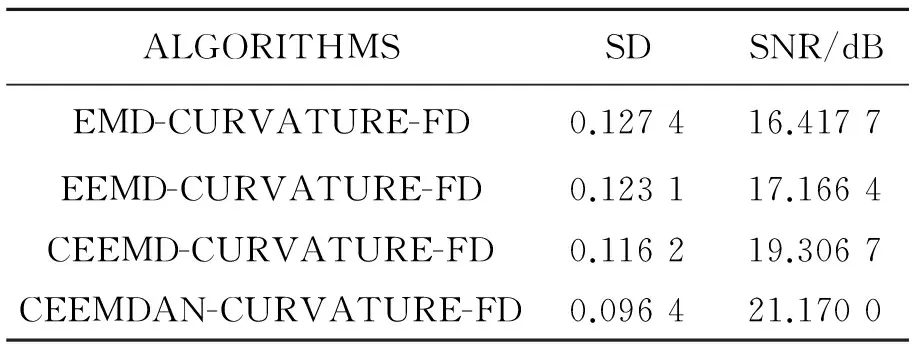
表2　4种基于EMD方法的信号重构效果

前文中实验表明CEEMDAN方法优于EMD、EEMD及CEEMD方法，更适合于非稳定信号的分解。针对信号y(t)，利用参考文献[20](CEEMDAN-MI)和[21](CEEMDAN-NMHD)中提出的去噪方法与本文的基于CEEMDAN的改进算法进行对比分析，去噪重构后的SD值及SNR如表3所示，由结果可知，CEEMDAN-CURVATURE-FD方法去噪后的SD值为0.096 4，SNR为21.170 0 dB，优于参考文献[20]和[21]中提出的去噪方法处理后的SD值(0.146 2，0.113 7)及SNR(17.083 6 dB，18.892 4 dB)，即重构误差小，去噪能力强。

表3　不同方法的去噪效果(SNRin=5 dB)

4.2实测信号实验结果

在近红外无创血糖检测实验中，用葡萄糖溶液暂代血糖溶液，本实验中所有葡萄糖溶液均为在同一条件下统一配置的连续均匀分布的液体，浓度范围为50～1 000 mg/dL。所有近红外光谱实验数据由傅里叶光谱仪采集，满足朗伯比尔定律测量原理。

近红外光谱信号属于非稳态信号，可以采用基于CEEMDAN的改进算法去除信号中的干扰噪声，取500 mg/dL葡萄糖溶液作为研究对象，以其光谱数据去噪结果为例，如图10所示(彩图见期刊电子版)。

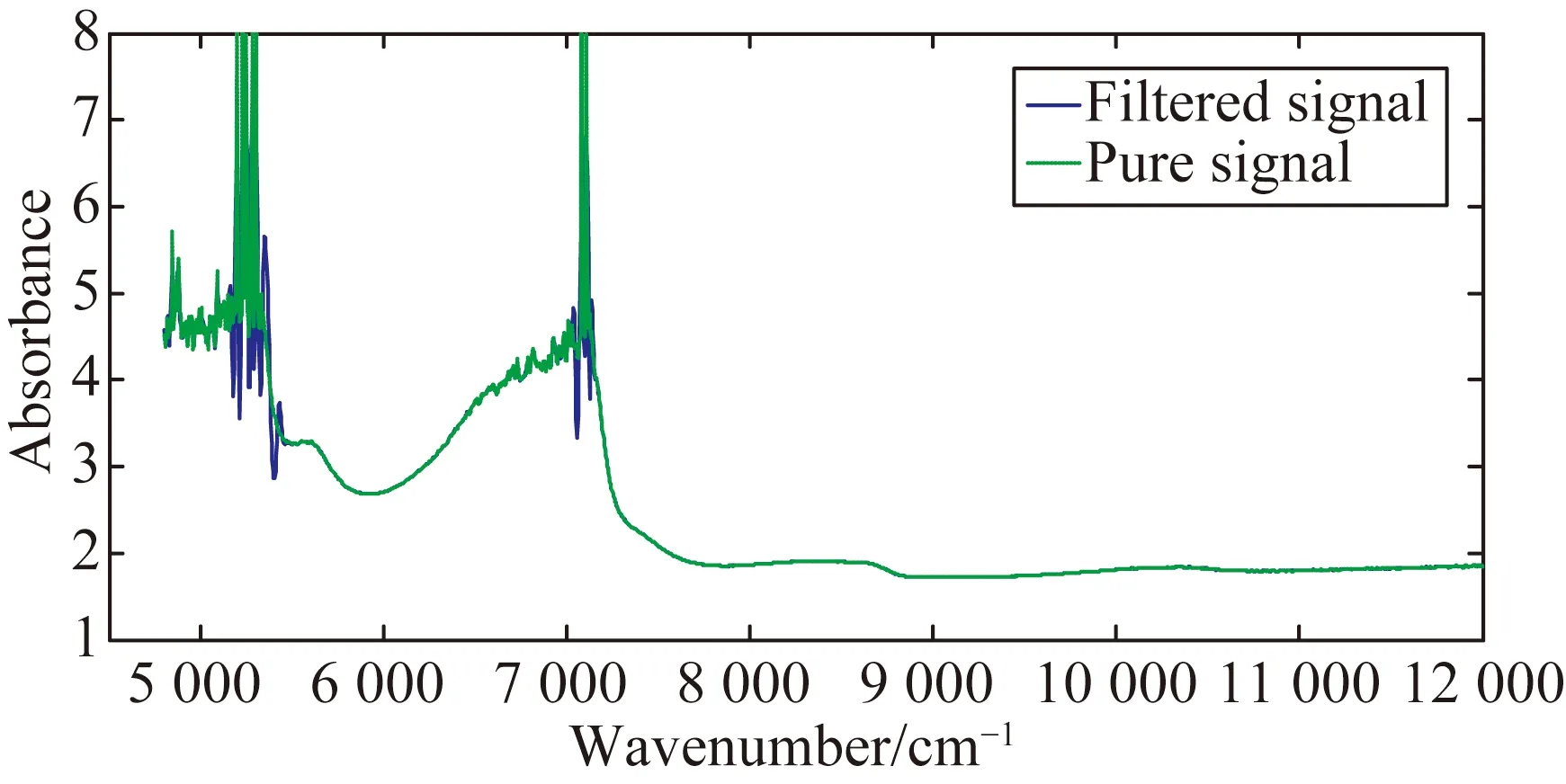
图10　原始信号及去噪结果(500 mg/dL)

为了验证上述算法的有效性，引入SNR和SD作为评价指标。由于用含噪信号代替公式(12)和公式(13)中的纯净信号y(n)，所以评价的衡量标准与仿真信号的评价标准相反，即SNR值越小，SD值越大，算法去噪效果越好。图11(彩图见期刊电子版)所示为通过不同方法进行光谱信号去噪处理后的SNR值和SD值对比图，由图可知，CEEMDAN-CURVATURE-FD方法优于其它3种方法。

图11　光谱信号的SNR和SD(500 mg/dL)

为了验证所提方法对光谱数据处理的普遍性，任意抽取10组样本的光谱数据，利用4种方法分别对其进行去噪处理，SNR和SD值结果如表4和表5所示(表中Method1代表EMD-CURVATURE-FD方法，Method2代表EEMD-CURVATURE-FD方法，Method3代表CEEMD-CURVATURE-FD方法，Method4代表CEEMDAN-CURVATURE-FD方法)。由实验结果可知，CEEMDAN-CURVATURE-FD方法适用于近红外光谱数据的去噪处理。

表4不同浓度样本光谱数据经4种方法处理后的标准差值

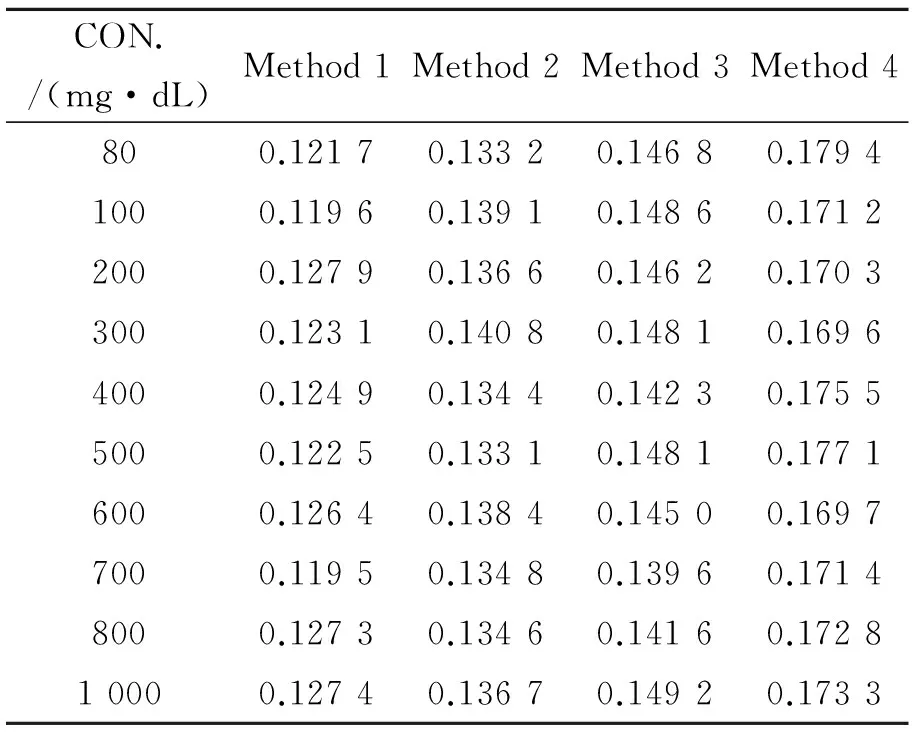
Tab.4　　　　SD of spectra data for sample with different concentrations by four methods　(dB)

表5不同浓度样本光谱数据经4种方法处理后的信噪比

Tab.5　　　　SNR of spectra data for sample with different concentrations by four methods　(dB)

5　结　论

本文提出了一种应用于近红外光谱的自适应去噪算法。首先利用EMD及其3种改进方法对仿真信号和由傅里叶光谱仪采集的葡萄糖溶液的光谱数据进行分解，然后求得原始信号及分解后IMFs的曲率曲线，并根据原始信号曲率和分解后IMFs曲率间的离散弗雷歇距离选择相关模态，最后进行信号重构。将SNR和SD值作为评价指标。实验结果显示，对于近红外光谱信号，CEEMDAN-CURVATURE-FD方法处理后的SD值为0.179 4，SNR值为19.117 5 dB，结果优于其它3种方法，该方法适用于红外光谱数据的去噪。

[1]do AMARAL C E F， WOLF B. Current development in non-invasive glucose monitoring [J].Medical.Engineering&Physics， 2008，30(5)：541-549.

[2]DU NCAN A， HANNIGAN J， FREEBORN S S，etal..A portable non-invasive blood glucose monitor [C].The8thInternationalConferenceonSolid-StateSensorsandActuators， 1995， 2：455-458.

[3]BLANCO J R， FERRERO F J， CAMPO J C，etal.. Design of a low-cost portable potentiostat for amperometric biosensors [C]. 2006IEEEInstrumentationandMeasurementTechnologyConferenceProceedings， 2006： 690-694.

[4]UNNIKRISHNA K A， HEMACHANDRAN D， ABHISHEK T K. A survey on non-invasive blood glucose monitoring using NIR [C].2013InternationalConferenceonCommunicationsandSignalProcessing(ICCSP)， 2013：1069-1072.

[5]周玲芳， 陈菲. 基于斜率差值的自适应图像椒盐噪声滤波算法[J]. 液晶与显示， 2015， 30(4)：695-700.

ZHOU L F， CHEN F. Adaptive slope difference algorithm for filtering salt and pepper noise in image [J].ChineseJournalofLiquidCrystalsandDisplays， 2015，30(4)： 695-700.(in Chinese)

[6]董雪，林志贤， 郭太良. 基于LoG算子改进的自适应阈值小波去噪算法[J]. 液晶与显示， 2014， 29(2)：275-280.DONG X， LIN ZH X， GUO T L. Improved self-adaptive threshold wavelet denoising analysis based on LoG operator [J].ChineseJournalofLiquidCrystalsandDisplays， 2014，29(2)： 275-280.(in Chinese)

[7]李权， 赵勋杰， 彭青艳，等. 基于主成分分析法的窗口自适应粒子滤波算法[J]. 红外与激光工程， 2014， 43(10)：3474-3479.

LI Q， ZHAO X J， PENG Q Y，etal.. Windows adaptive particle filter algorithm based on principal component analysis [J].InfraredandLaserEngineering， 2014， 43(10)：3474-3479.(in Chinese)

[8]顾有林， 叶应流， 曹光华，等. EMD和小波变换在低可探测目标检测中的应用 [J]. 红外与激光工程， 2015， 44(11)：3494-3499.

GU Y L， YE Y L， CAO G H，etal.. Application of EMD and wavelet transform in low detectable targets detection [J].InfraredandLaserEngineering， 2015，44(11)：3494-3499.(in Chinese)

[9]HUANG N E. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J].Proc.R.Soc.Lond.A，1998， 454：903-995.

[10]李欣，梅德庆，陈子辰. 基于经验模态分解和希尔伯特-黄变换的精密孔镗削颤振特征提取[J].光学 精密工程， 2011，19(6)： 1291-1297.

LI X，MEI D Q，CHEN Z CH.Feature extraction of chatter for precision hole boring processing based on EMD and HHT [J].Opt.PrecisionEng.， 2011，19(6)： 1291-1297.(in Chinese)

[11]REN Y， SUGANTHAN P N， SRIKANTH N. A comparative study of empirical mode decomposition-based short-term wind speed forecasting methods [J].IEEETransactionsonSustainableEnergy2015， 6(1)： 236-244.

[12]鲁丽，颜国正，赵凯，等. 基于集合经验模态分解的人体结肠动力分析[J].光学 精密工程， 2015，23(6)： 1850-1856.LU L， YAN G ZH， ZHAO K，etal.. Analysis of human colonic motility using EEMD [J].Opt.PrecisionEng.， 2015，23(6)： 1850-1856.(in Chinese)

[13]GAN Y， SUI L， WU J，etal.. An EMD threshold denoising method for inertial sensors [J].Measurement，2014， 49(1)， 34-41.

[14]罗玉昆，罗诗途，罗飞路，等. 激光超声信号去噪的经验模态分解实现及改进[J].光学 精密工程， 2013，21(2)： 479-487.LUO Y K， LUO SH T， LUO F L，etal.. Realization and improvement of laser ultrasonic signal denoising based on empirical mode decomposition[J].Opt.PrecisionEng.， 2013，21(2)： 479-487.(in Chinese)

[15]MARIA E T， MARCELO A C， GASTON S，etal.. A complete ensemble empirical mode decomposition with adaptive noise [C]. 2011IEEEInternationalConferenceonAcoustics，SpeechandSignalProcessing(ICASSP)， 2011： 4144-4147.

[16]JIA R Y， JIANN S S. Complementary ensemble empirical mode decomposition： A novel noise enhanced data analysis method [J].AdvancesinAdaptiveDataAnalysis， 2010， 2(2)：135-156.

[17]ANNE H H， PIERRE A， GUILLAUME M，Analysis of laser speckle contrast images variability using a novel empirical mode decomposition： comparison of results with laser Doppler flowmetry signal variability [J].IEEETransactionsonMedicalImaging， 2015， 34(2)：618-626.

[18]COOLIDGE J L. The unsatisfactory story of curvature [J].TheAmericanMathematicalMonthly， 1952， 59(6)： 375-379.

[19]R S， KARTHIK K， CHIRANJIB B. Frechet distance based Approach for searching online handwritten documents [C].NinthInternationalConferenceonDocumentAnalysisandRecognition，(ICDAR)，2007.

[20]HAN L， LI C， LIU H. Feature extraction method of rolling bearing fault signal based on EEMD and cloud model characteristic entropy [J].Entropy， 2015， 17(10)：6683-6697.

[21]LI C， ZHAN L. A hybrid filtering method based on a novel empirical mode decomposition for friction signals [J].MeasurementScience&Technology， 2015， 26(12)：125003.

李晓莉(1984-)，女，黑龙江哈尔滨人，博士研究生，2008年、2011年于东北农业大学分别获得学士、硕士学位，主要从事无创血糖检测及胰岛素注射剂量调节研究。E-mail： xiaoli72460@163.com

导师简介：

李成伟(1963-)，男，黑龙江哈尔滨人，博士，教授，1985年、1988年、2000年于哈尔滨工业大学分别获得学士、硕士、博士学位，主要从事生物医学工程、智能控制技术研究。E-mail： lcw@hit.edu.cn

(版权所有未经许可不得转载)

Application of improved complete ensemble empirical mode decomposition with adaptive noise in spectral signal denoising

LI Xiao-li， LI Cheng-wei*

(SchoolofElectricalEngineeringandAutomation，HarbinInstituteofTechnology，Harbin150001，China)

*Correspondingauthor，E-mail：lcw@hit.edu.cn

As the accuracy and stability of a blood glucose level model is affected by the noise in near infrared non-invasive blood glucose detection process, an improved complete ensemble empirical mode decomposition method with adaptive noise was proposed for denoising of near infrared spectroscopy signals. Meanwhile, a mode selection method based on Frechet distance combining with the feature of curve curvature was proposed for the selection of Intrinsic Mode Functions(IMFs). Firstly. the complete ensemble empirical mode decomposition method with adaptive noise was introduced in the denoising processing of near infrared spectroscopy, and the basic principles and concrete realization processes of empirical mode decomposition, ensemble empirical mode decomposition, complementary ensemble empirical mode decomposition and the complete ensemble empirical mode decomposition based on adaptive noise were described. Then, an improved complete ensemble empirical mode decomposition method with adaptive noise based on curvature and discrete Frechet distance was applied in denoising for simulation signals and spectral signals， and their standard deviation and the Signal to Noise Ratio(SNR) were taken as the evaluation indexes. The simulation and experimental results show that the standard deviation of the improved method based on curvature and discrete Frechet distance in the near infrared spectral signal is 0.179 4, and the SNR is 19.117 5 dB, which extracts useful information, realizes the separation of signal and noise, and improves the quality of reconstructed signals. The proposed method has a good adaptability to effectively identify and separate the signal and noise components.

non-invasive blood glucose detection; near infrared spectroscopy; signal denoising; Complete Ensemble Empirical Mode Decomposition with Adaptive Noise(CEEMDAN); curvature; discrete Frechet distance

2016-03-10；

2016-04-25.

哈尔滨市科技创新人才专项资金资助项目(No.2014RFXXJ065)；哈尔滨工业大学理工医交叉学科基础研究培育计划资助项目(No.HIT.IBRSEM.201307)

1004-924X(2016)07-1754-09

O657.33；R587.1

Adoi:10.3788/OPE.20162407.1754