应用分数低阶循环相关估计单电磁矢量传感器的波达方向和极化参数
石屹然,赵晓晖,李新波,石要武
(1. 吉林大学 通信工程学院, 吉林 长春 130022;2. 长春气象仪器研究所, 吉林 长春 130012;3. 吉林大学 生物与农业工程学院, 吉林 长春 130022)
应用分数低阶循环相关估计单电磁矢量传感器的波达方向和极化参数
石屹然1,2,赵晓晖1,李新波1,石要武3
(1. 吉林大学 通信工程学院, 吉林 长春 130022;2. 长春气象仪器研究所, 吉林 长春 130012;3. 吉林大学 生物与农业工程学院, 吉林 长春 130022)
提出了一种在α和高斯混合噪声以及循环平稳干扰并存背景下基于分数低阶循环相关(FLOCC) 联合估计单电磁矢量传感器波达方向(DOA)和极化参数的多重信号分类(MUSIC)方法。该方法利用信号的循环平稳特性,采用分数低阶循环相关函数抑制α和高斯混合噪声以及循环平稳干扰信号;然后利用MUSIC方法对单电磁矢量传感器的DOA和极化参数进行联合估计,并利用DOA参数与极化参数的相互独立性,将传统MUSIC方法的四维搜索简化为两次二维搜索,从而有效地减少该算法的计算量。对所提算法与基于分数低阶矩的MUSIC算法进行了实验对比。结果显示:提出的方法可充分地抑制与待测信号循环频率相异的任意循环平稳干扰信号;在α和高斯混合信噪比为0 dB,信干比为3 dB 时,估计得到的DOA和极化参数的均方根误差分别为0.3°和0.7°,明显优于基于分数低阶矩的MUSIC方法。
单电磁矢量传感器;波达方向;极化参数;参数估计;分数低阶循环相关
1 引 言
电磁矢量传感器是由三维电偶极子和三维磁偶极子共点正交构成的[1],它可以获得完备的入射电磁信号的三维电场信息和三维磁场信息,具有空间占用率低、可靠性强、各分量间无需进行位置校准以及时间同步等一系列优点。特别是单个电磁矢量传感器就可以实现入射电磁信号的波达方向(Direction Of Arrival, DOA)和极化参数估计,因而在机(弹)载雷达中得到了广泛的应用。
目前,单电磁矢量传感器的DOA和极化参数估计问题已得到了相关学者们的广泛关注和深入研究,并取得了大量的科研成果。Nehorai等人提出了单电磁矢量传感器接收信号的数学模型[1]。文献[2]提出了一种基于单电磁矢量传感器的时变信号DOA和极化参数估计方法;文献[3]提出了基于单电磁矢量传感器的多源信号DOA和极化参数联合估计的ESPRIT方法;文献[5]利用循环相关和高阶累积量算法,分别提出了基于单电磁矢量传感器的DOA和极化参量联合估计的子空间-最小范数方法。
上述这些单电磁矢量传感器DOA和极化参数估计方法都是建立在测量背景噪声为高斯噪声(有色或无色)假设基础上的。然而,通过分析大量的阵列信号DOA估计的实际应用环境,人们发现,在其测量环境中,不仅存在着高斯噪声,同时还存在大量的非高斯冲击噪声。例如,由雷电引起的大气噪声,电力传输线的电压瞬变噪声,电话线的切换冲击噪声,无线通信中的信号窜扰噪声,海浪和水下生物引起的水下声学噪声[6-7],以及在电子战中,针对机(弹)设备所施放的人为干扰和噪声[8-10]等等。Nikias指出,这种非高斯的冲击噪声符合α稳定分布[11],所以一般称这种非高斯的冲击噪声为α稳定分布噪声(简称为α噪声)。α稳定分布是唯一一种满足广义中心极限定理(Generalized Central Limit Theorem, GCLT)的广义高斯分布族。它的一个最重要的性质是它不存在p>α的统计量[11],当α<1时,甚至连均值的运算也不可能。因此,在存在α噪声的场合,上述那些基于二阶矩、高阶矩和高阶累积量的阵列信号DOA估计方法均失效。
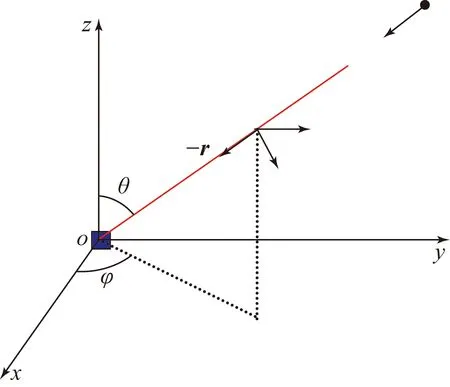
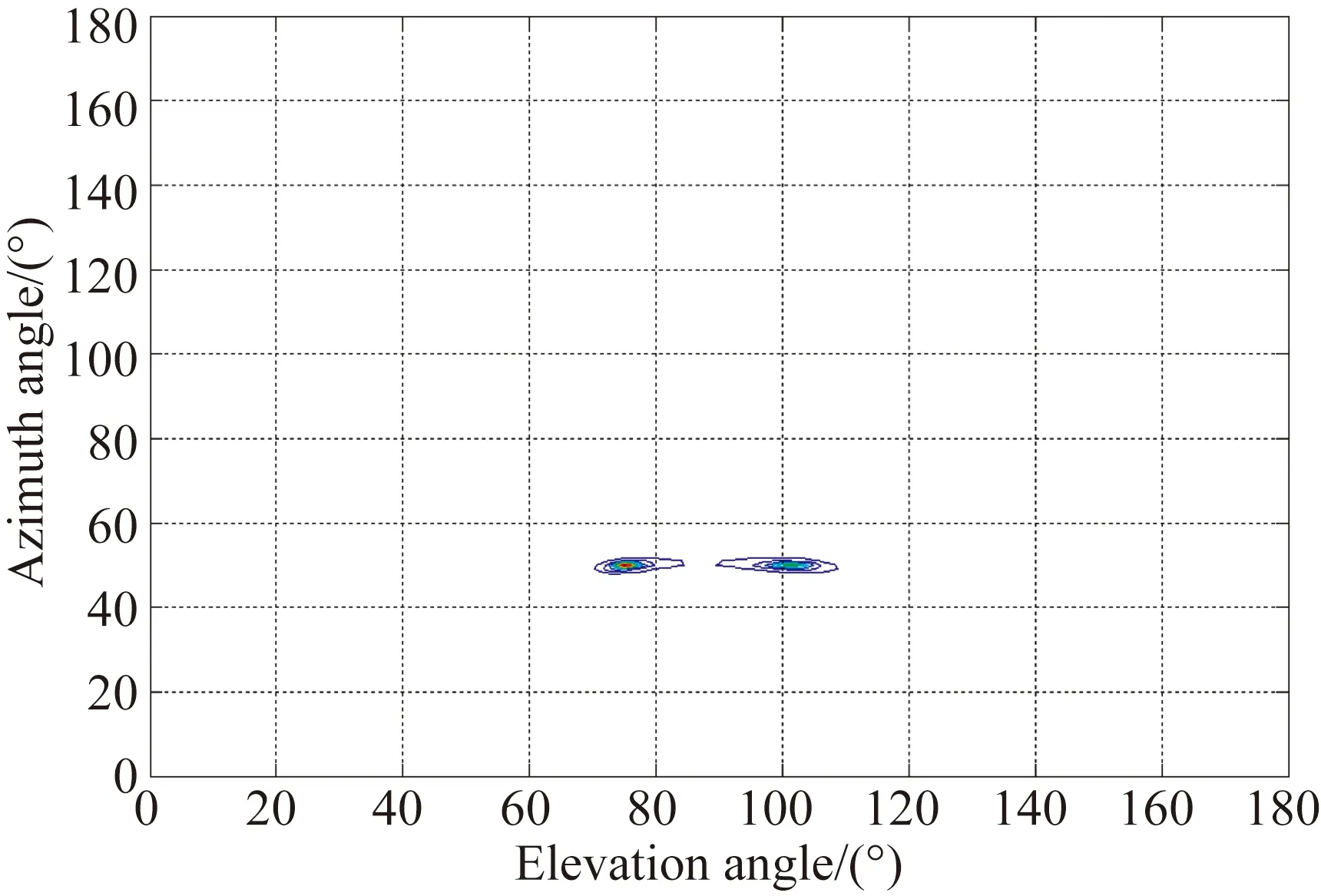
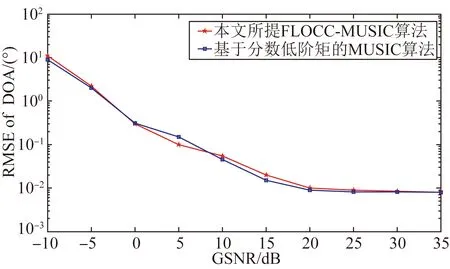
由于α稳定分布存在着0 但经过α噪声背景下阵列信号DOA估计的大量实践,分数低阶矩方法的弊病逐渐暴露出来:首先,分数低阶矩是一种非线性方法[11],它不存在半不变性,即两个相互独立的随机变量的和的分数低阶矩不等于随机变量各自的分数低阶矩的和,这给信号和噪声的分离造成了很大的困难;此外,α噪声的分数低阶矩恒不为零,这说明分数低阶矩的噪声抑制能力较差,这也直接影响了阵列信号DOA估计性能;再者,现有的基于分数低阶矩类阵列信号DOA估计的子空间方法均要求附加噪声须为零均值独立同分布(i.i.d)的SαS稳定分布情况,且要求α稳定分布的特征指数为1<α≤2,因此具有很大的局限性。针对这一问题,本文提出了基于分数低阶循环相关(Fractional Low order Cyclic Correlation, FLOCC)[23]的单电磁矢量传感器DOA估计的多重信号分类(MUSIC)方法(FLOCC-MUSIC),该方法可有效抑制包括α和高斯噪声在内的任何异于信号循环频率的平稳噪声及干扰信号,从而可大大提高单电磁矢量传感器DOA和极化参数的估计性能。 设单电磁矢量传感器位于坐标原点,其三维电偶极子和三维磁偶极子的法线分别平行于直角坐标系的3个坐标轴(即x.y.z轴)。设一远场单位能量横平面电磁波入射到单电磁矢量传感器。如图1所示,r为单位矢量,入射信号的DOA为(θ,φ),其极化参数为(γ,η)。则单电磁矢量传感器的接收信号模型可以表示为[24]: (1) 图1 空间电磁信号传播坐标示意图 Fig.1Schematic diagram of electromagnetic signal propagation in space 设空域内有K个独立的远场极化信号,入射到单电磁矢量传感器的波达角度为(θk,φk),极化状态为(γk,ηk),k=1,2,…,K。则单电磁矢量传感器的接收信号可表示为: (2) 不失一般性,这里假设: (3)α噪声的特征指数α已知。 (4)诸Sk(t)之间统计循环独立。 3单电磁矢量传感器DOA和极化 参数联合估计的FLOCC-MUSIC 方法 设单电磁矢量传感器的输出信号如式(2)所示。则输出信号X(t)的分数低阶循环相关函数矩阵为: (3) 式中:ω为循环频率,如前假设,它是已知的; p(p<α)表示分数低阶矩的阶次;上标H表示共轭转置。 (4) 式中上标*表示共轭。 式(4)中,根据前文所述信号假设以及分数低阶循环相关函数的性质可知[23],对于循环频率ω,只有K个接收信号Sk(t)存在循环自相关,而其余各项均为零。则式(4)可表示为: (5) 由于诸Sk(t)之间统计循环独立,因此: (6) 式中: 将式(6)代入式(3),经整理可得: (7) 式中: 矩阵A=[a1,a2,…,ak],为导向矢量阵。 (8) σ1≥σ2…≥σ6. (9) σ1≥σ2…≥σK≥σK+1=…=σ6=0. (10) 令 Σ1=diag[σ1,σ2,…,σK]. (11) 则式(8)可写成: (12) (13) (14) (15) (16) 显然,V1、U1均为p×K维矩阵,V2、U2均为p×(p-K)维矩阵。将式(13)~(16)代入式(12),得: (17) 将上式两端右乘V2,可得: (18) 将式(7)代人式(18)可得: AHV2=0. (19) 这说明信号导向矢量阵A与噪声矢量空间V2中任一噪声奇异矢量Vi∈V2均正交,因此由下式即可得到入射信号的二维DOA和极化参数估计[24]: (20) 注意到(20)中矩阵Z(θ,φ)与极化参数(γ,η)相互独立,所以,当参数搜索使得Z(θ,φ)奇异时,式(20)的分母为零,P(θ,φ,γ,η)出现峰值。因此,入射信号S(t)的DOA参数可通过下式的二维搜索得到: (21) (22) 对比式(20)、(21)和(22),本文将传统MUSIC方法的搜索转化为两次二维搜索,从而极大程度地降低了参数搜索的计算量。 本节通过仿真实验考查提出的单电磁矢量传感器DOA和极化参数联合估计的FLOCC-MUSIC方法的参数估计性能及对干扰信号和噪声的抑制能力。 4.1实验1 实验目的:验证本文所提算法在α和高斯有色噪声以及循环平稳干扰信号并存情况下的DOA和极化参数估计能力。 实验条件:设一个远场待测循环平稳AM信号S1的入射角为θ1=75°,φ1=50°,其载波频率为fC1=15 MHz,极化参数为γ1=45°,η1=45°;另一个循环平稳AM干扰信号S2以入射角θ2=120°,φ2=50°入射到单电磁矢量传感器上,其载波频率为fC2=11 MHz,极化参数为γ2=80°,η2=90°;附加噪声nα(t)为SαS稳定分布噪声,它是按文献[25]方法产生,α=1.6,其信噪比采用广义信噪比(GSNR)[25]定义;ng(t)为由高斯分布白噪声通过一个四阶带通滤波器产生的零均值高斯平稳有色噪声,其信噪比(Signal to Noise Ratio, SNR)记为SNgR。取混合信噪比SNR=GSNR+SNgR=10 dB(GSNR=SNgR),信干比(SIR)=3 dB,采样频率fs为100 MHz,快拍数为1 000。 算法参数设置:取分数低阶循环相关函数的阶次P=1.4;循环频率ω选为4fC1=60 MHz。 实验方法:使用本文提出的FLOCC-MUSIC方法执行100次独立的Monte Carlo实验。 图2和图3为其中一次典型的参数估计实验结果。 (a)三维图 (b)等高线图 (a)三维图 (b)等高线图 从图2和图3中可以看出,在α稳定分布噪声和高斯有色噪声以及与待测信号循环频率相异的循环平稳干扰信号共同存在的背景下,本文所提出的FLOCC-MUSIC方法能够对背景噪声以及干扰信号进行有效地抑制。并且在SNR=10 dB,SIR=3 dB时,仍然能以较高的精度估计出入射信号的DOA和极化参数。 4.2实验2 实验目的:与目前被业内普遍认可的文献[18]中的基于分数低阶矩的MUSIC算法进行对比仿真实验,以在测量环境中存在循环平稳干扰信号的情况下,验证本文所提方法对DOA和极化参数估计的优越性。 实验条件:采用与实验1完全相同的实验条件。 算法参数设置:取分数低阶矩的阶次P=1.4。 实验方法:文献[18]中的基于分数低阶矩的MUSIC算法,执行100次独立的Monte Carlo实验。 图4、图5给出了待测信号S1的DOA和极化参数估计一次典型实验结果。 (a)三维图 (b)等高线图 (a)三维图 (b)等高线图 Fig.5Polarization parameters estimation of fractional lower order moment-based MUSIC method(SNR=10 dB,SIR=3 dB) 将实验1和实验2的仿真结果进行对比,可以明显看出,基于分数低阶矩的MUSIC方法虽然可以估计出信号的DOA和极化参数,且有效地抑制了α噪声和高斯有色噪声,但在循环平稳AM干扰信号S2处,却出现了明显的伪峰。这说明本文所提的FLOCC-MUSIC方法对于分离和抑制不同循环频率干扰信号的能力明显优于基于分数低阶矩的MUSIC算法。 4.3实验3 实验目的:在不同信噪比条件下对本文所提FLOCC-MUSIC算法与文献[18]中基于分数低阶矩算法进行均方根误差对比试验,以验证本文所提算法的参数估计性能。 实验条件:采用与实验1完全相同的实验条件。令信干比保持不变,即SIR=3 dB;混合信噪比SNR从0 dB到35 dB以5 dB为间隔变化。 算法参数设置:文献[18]与本文算法的阶次均取P=1.4;本文算法中的循环频率ω选为4fC1=60 MHz。 实验方法:在相同的实验条件下,将两种算法分别执行100次独立的Monte Carlo实验。以均方根误差(Root Mean Square Error, RMSE)作为评判准则,则DOA和极化参数的RMSE计算公式如下: (23) (24) 图6 DOA估计的均方根误差曲线 图7 极化参数估计的均方根误差曲线 信号S1的DOA和极化参数估值的均方根误差随混合信噪比变化的曲线如图6和图7所示。 从图6和图7中可以看出,随着混合信噪比的逐渐增加,本文所提FLOCC-MUSIC算法的DOA和极化参数估值的均方根误差逐渐减小;即使在混合信噪比为0dB情况下,本文所提算法的参数估值均方根误差仍然较低(其DOA和极化参数估计的均方根误差分别为0.3°和0.7°)。对于入射信号S1,本文所提算法与基于分数低阶矩的MUSIC方法的参数估计效果整体相当;但是对于循环平稳干扰信号S2,基于分数低阶矩的MUSIC方法产生了错误的估计。这充分说明,本文所提的FLOCC-MUSIC方法可以有效地抑制与待测信号循环频率相异的附加干扰信号以及α噪声和高斯有色噪声对单电磁矢量传感器的DOA和极化参数联合估计精度的影响。 本文主要研究了在循环平稳干扰信号以及α和高斯混合噪声并存背景下的单电磁矢量传感器DOA和极化参数估计问题。提出了一种基于单电磁矢量传感器的DOA和极化参数联合估计的FLOCC-MUSIC方法。该方法利用入射信号的循环平稳特性,充分抑制了α和高斯混合噪声及与信号循环频率相异的任何循环平稳信号的干扰。在α和高斯混合信噪比为0 dB,信干比为3 dB 时,其DOA和极化参数估计的均方根误差分别为0.3°和0.7°。仿真结果验证了本文方法对α和高斯混合噪声及干扰信号的抑制能力及参数估计的有效性。 [1]NEHORAI A, PALDI E. Vector-sensor array processing for electromagnetic source localization [J].IEEETransactionsonSignalProcessing, 1994, 42(2): 376-398. [2]刘扬, 吴瑛. 机载单电磁矢量传感器时变信号参数估计算法 [J]. 电路与系统学报, 2012, 17(1): 54-59. LIU Y, WU Y. Time-varying signal parameter estimation algorithm for airborne single electromagnetic vector sensor [J].JournalofCircuits&Systems, 2012,17(1): 54-59.(in Chinese) [3]WONG K T, ZOLTOWSKI M D. Uni-vector-sensor ESPRIT for multisource azimuth, elevation, and polarization estimation [J].IEEETransactionsonAntennas&Propagation, 1997, 45(10): 1467-1474. [4]王洪洋, 王兰美, 廖桂生. 基于单矢量传感器的信号多参数估计方法 [J]. 电波科学学报, 2005, 1(1): 15-19. WANG H Y, WANG L N, LIAO G SH. Parameter estimation of multiple source based on uni vector-sensor [J].ChineseJournalofRadioScience, 2005, 1(1): 15-19. [5]石屹然. 有色噪声背景下极化阵列信号参数估计方法研究 [D]. 兰州: 兰州理工大学, 2010. SHI Y R.Studyonmethodsofparameter-estimationofpolarizationsensitivearraysignalincolorednoise[D]. Lan Zhou: Lan Zhou University of Technology, 2010(in Chinese) [6]MOGHIMI F, NASRI A, SCHOBER R. Lp-norm spectrum sensing for cognitive radio networks impaired by non-Gaussian noise [C].ProceedingsoftheGlobalTelecommunicationsConference,GLOBECOMIEEE, 2009:1-6. [7]KASSAM S A.SignalDetectioninNon-GaussianNoise[M]. Berlin: Springer, 2012. [8]吕泽均, 肖先赐. 在冲击噪声环境中基于子空间的测向算法研究 [J].航空学报, 2003, 24(2): 174-177. LU Z J, XIAO X C. Study on subspace-based direction finding algorithm in the presence of impulsive noise environments[J].ActaAeronauticaEtAstronauticaSinica, 2003, 24(2): 174-177.(in Chinese) [9]孟勃, 韩广良, 李波. 雷达告警态势图在小型舰船跟踪预警系统中的应用[J].液晶与显示, 2014, 29(6): 1131-1138. MENG B, HAN G L, LI B. Radar warning situation map using in photoeletric tracking system [J].ChineseJournalofLiquidCrystals&Displays, 2014, 29(6): 1131-1138.(in Chinese) [10]苏爱东, 高维珉. 一种航迹跟踪雷达模拟系统软件设计与实现[J].液晶与显示, 2015, 30(1): 95-102. SU A D, GAO W M. Software design and implement of flight track radar modeling system [J].ChineseJournalofLiquidCrystals&Displays, 2015, 30(1): 95-102.(in Chinese) [11]SHAO M, NIKIAS C L. Signal processing with fractional lower order moments: stable processes and their applications [J].ProceedingsoftheIEEE, 1993, 81(7): 986-1010. [12]丘天爽, 张旭秀, 李小兵,等. 统计信号处理-非高斯信号处理及其应用 [M]. 北京:电子工业出版社, 2004QIU T SH, ZHANG X X, LI X B,etal..StatisticalSignalProcessing-NonGaussSignalProcessingandApplication[M]. Beijing: Publishing House of Electronics Industry, 2004.(in Chinese) [13]TSAKALIDES P, NIKIAS C L. Robust adaptive beamforming in alpha-stable noise environments [C]. 1996IEEEInternationalConferenceonProceedingsoftheAcoustics,Speech,andSignalProcessing,ICASSP-96ConferenceProceedings, 1996:2884-2887. [14]TSAKALIDES P, NIKIAS C L. Space-time adaptive processing in stable impulsive interference; proceedings of the Signals [C].1996ConferenceRecordoftheThirtiethAsilomarConferenceonSystemsandComputers, 1997:3517-3517. [15]TSAKALIDES P, NIKIAS C L, TSAKALIDES P,etal.. Maximum likelihood localization of sources in noise modeled as a Cauchy process[C]MilitaryCommunicationsConference,MILCOM’94.ConferenceRecord, 1994:613-617. [16]TSAKALIDES P, NIKIAS C L. Wideband array signal processing with alpha-stable distributions [C].ProceedingsoftheMilitaryCommunicationsConference,MILCOM’95,ConferenceRecord,IEEE,F, 1995 [17]TSAKALIDES P, NIKIAS C L. The robust covariation-based MUSIC(ROC-MUSIC) algorithm for bearing estimation in impulsive noise environments [J].ProcessingIEEETransactionsonSignal, 1996, 44(7): 1623-1633. [18]LIU T H, MENDEL J M. A subspace-based direction finding algorithm using fractional lower order statistics [J].ProcessingIEEETransactionsonSignal, 2001, 49(8): 1605-1613. [19]KANNAN B, FITZGERALD W J, KANNAN B,etal.. Joint Bayesian estimation of DOA and frequency of BPSK(binary phase shift keying) signals in α-stable noise [C]. 1999ProceedingsofICECS’99,The6thIEEEInternationalConferenceonElectronics,CircuitsandSystems, 1999: 1771-1774. [20]KANNAN B, FITZGERALD W J, KURUOGLU E E. Joint DOA, frequency and model order estimation in additiveα-stable noise [C].IEEEInternationalConferenceonAcoustics,Speech,andSignalProcessingICASSP’00, 2000:3798-3801. [21]KANNAN B, FITZGERALD W J. Beamforming in additiveα-stable noise using fractional lower order statistics(FLOS) [C].ProceedingsofICECS’99The6thIEEEInternationalConferenceonElectronics,CircuitsandSystems, 1999:1755-1758. [22]何劲.α稳定分布噪声背景下阵列信号处理方法研究 [D]. 南京: 南京理工大学, 2007. HE J.Investigationonarraysignalprocessingamidα-stablenoise[D]. Nanjing: Nanjing University of Science and Technology, 2007.(in Chinese) [23]里红杰. 基于分数低阶循环相关的系统辨识及应用研究 [D]. 大连: 大连理工大学, 2007. LI H J.Systemidentificationandapplicationbasedonfractionallowerordercycliccorrelation[D]. Dalian: Dalian University of Technology, 2007.(in Chinese) [24]周欣. 复杂噪声背景下极化阵列信号参数估计的理论与方法研究 [D]. 长春: 吉林大学, 2009. ZHOU X.Studyontheoryandmethodofsignalparametersestimationwithpolarizationsensitivearrayincomplexnoise[D]. Chang Chun: Jilin University, 2009.(in Chinese) [25]CHAMBERS J M, C L. A Method for simulating stable random variables [J].JournaloftheAmericanStatisticalAssociation, 1976, 71(354): 340-344. 石屹然(1984-),男,吉林长春人,博士后,讲师,2010年于兰州理工大学获得硕士学位,2014年于吉林大学获得博士学位,现为吉林大学通信工程学院讲师,长春气象仪器研究所博士后,主要从事谐波恢复,ARMA参数辨识,DOA及极化参数估计,非线性模型预测控制等方面的研究。E-mail: shiyiran@jlu.edu.cn 赵晓晖(1957-),男,吉林长春人,教授,博士生导师,1982年、1989年于吉林工业大学分别获得学士、硕士学位,1993年于法国贡比涅科技大学获得博士学位,现为吉林大学通信工程学院院长,主要从事信号处理理论及在通信中的应用研究。E-mail: xhzhao@jlu.edu.cn (本栏目编辑:李自乐) (版权所有未经许可不得转载) Estimation of DOA and polarition parameters for single electromagnetic vector sensor based on FLOCC SHI Yi-ran1,2, ZHAO Xiao-hui1, LI Xin-bo1, SHI Yao-wu3 (1.CollegeofCommunicationEngineering,JilinUniversity,Changchun130022,China;2.ChangchunMeteorologicalInstrumentResearchInstitute,Changchun130012,China;3.CollegeofBiologicalandAgriculturalEngineering,JilinUniversity,Changchun130022,China) *Correspondingauthor,E-mail:xhzhao@jlu.edu.cn A Fractional Lower Order Cyclic Correlation (FLOCC)-based MUSIC method was proposed for estimation of the Direction of Arrival (DOA) and polarization parameters for a single electromagnetic vector sensor in mixedαand Gaussian noises and cycle stable interference signals. On the basis of the cyclic stability of signals, the FLOCC function was used to suppress the cyclic stationary disturbance signal and the mixedαand Gaussian noises. Then, MUSIC method was used to estimate the DOA and polarization parameters of the single electromagnetic vector sensor, and the mutual independence between the DOA parameters and the polarization parameters was used to simplify the four dimensional search of traditional MUSIC method into two times of two dimensional search to reduce the calculated amount of the algorithm. The proposed algorithm was compared with the traditional MUSIC method based on fractional lower order moment in the simulation. The results show that the proposed method can sufficiently suppress any of cyclic stationary disturbances with different cycle frequencies. When the mixed signal to noise ratio ofαand Gaussian noises is 0 dB and the signal to interference ratio is 3 dB, the root mean square error of the estimation of DOA and polarization parameters is 0.3° and 0.7 °, respectively, being superior to that of the traditional MUSIC method. single electro magnetic vector sensor; Direction of Arrival(DOA); polarization parameter; parameter estimation; Fractional Lower Order Cyclic Correlation(FLOCC) 2016-03-03; 2016-04-08. 国家自然科学基金资助项目(No.61571209) 1004-924X(2016)07-1818-09 TP212.13;TN911.23 Adoi:10.3788/OPE.20162407.18182 单电磁矢量传感器的接收信号模型


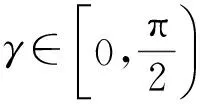
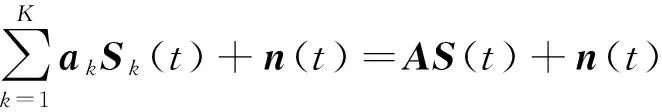


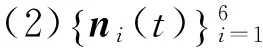
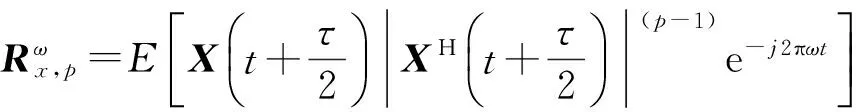



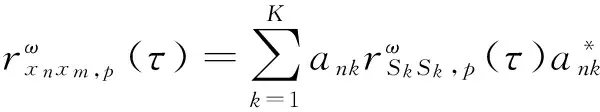
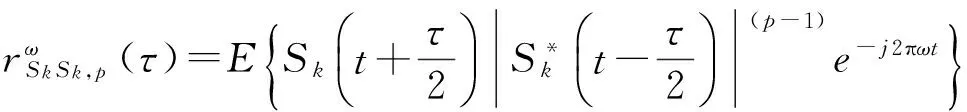
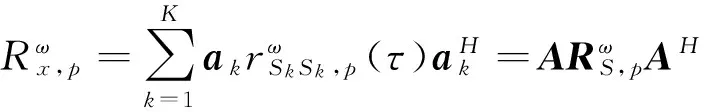


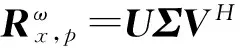

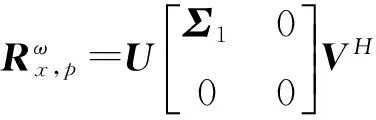

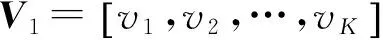
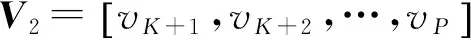




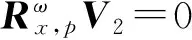

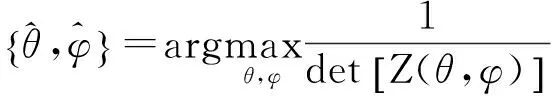
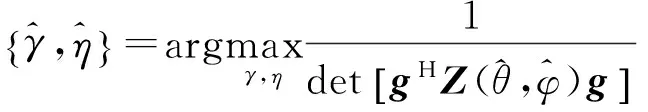
4 仿真实验







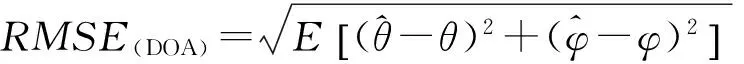


5 结 论



