两自由度悬臂梁压电发电装置的宽频发电性能

刘祥建，朱莉娅，陈仁文

(1.金陵科技学院 机电工程学院，江苏 南京 211169；2.南京师范大学 江苏省三维打印装备与制造重点实验室，江苏 南京 210042；3.南京航空航天大学 机械结构力学及控制国家重点实验室，江苏 南京 210016)



两自由度悬臂梁压电发电装置的宽频发电性能

刘祥建1*，朱莉娅2，陈仁文3

(1.金陵科技学院 机电工程学院，江苏 南京 211169；2.南京师范大学 江苏省三维打印装备与制造重点实验室，江苏 南京 210042；3.南京航空航天大学 机械结构力学及控制国家重点实验室，江苏 南京 210016)

研究一种两自由度悬臂梁压电发电装置，以提高悬臂梁式压电发电装置在环境振源振动频率波动情况下的发电能力。建立了两自由度悬臂梁压电发电装置的频率特性理论模型，并对该理论模型进行了有限元仿真验证，结果显示理论计算与有限元仿真结果基本一致。对两自由度悬臂梁压电发电装置的频率特性模型进行了数值模拟，模拟显示：装置的前两阶模态频率比随着长度比、宽度比、厚度比及质量块的质量比的增大均出现一个最小值，且在长度比为0.8，宽度比为2.0，厚度比为1.0，质量块的质量比为0.5时，装置的前两阶模态频率比最小，结果表明通过合理设计两自由度悬臂梁压电发电装置的结构参数，可以使得装置的前两阶模态频率最接近。最后，实例设计了两自由度悬臂梁压电发电装置，并进行了试验测试，证实了优化后的两自由度悬臂梁压电发电装置具有宽频带发电能力。

压电发电装置；两自由度悬臂梁；宽频带；频率特性

1　引　言

近年来，随着电子技术和网络信息技术的飞速发展，无线传感器网络在智能交通、环境监控及航空航天等领域的应用日益广泛。微电子技术及微细加工技术的快速发展，大大降低了无线传感器节点的能耗，目前的无线传感器节点可以微瓦级平均功率工作。但是化学电池供能过程中使用寿命有限，电池废弃物易造成环境污染，这对于野外及不方便更换电池场合中的无线传感器节点，限制了其推广应用。振动发电技术作为一种新型能源方式，得到了进一步发展及其实际应用。目前，用于振动发电的方式主要有压电式[1-12]、电磁式[13-14]和静电式[15-16]，其中，压电式振动发电装置以其易于微型化、无污染及容易实施等优点而成为研究热点。

随着对压电式振动发电技术研究的展开和深入，出现了各种压电振动发电装置。2004年，Kim等人研究了Cymbal型压电振动发电装置[5]，通过优化设计，可以获得39 mW的输出功率；2005年，Roundy等人建立了单悬臂梁压电发电装置发电理论模型[3]，并对其发电性能进行了分析；2006年，Shahruz研究了悬臂梁阵列式压电振动发电装置[4]，研究表明，通过合理的结构参数设计，可以达到拓宽装置频带的目的；2009年，Erturk等人研究了L型压电振动发电装置[6]，研究发现，通过合理的结构尺寸设计，可以拉近装置的前两阶固有频率，达到宽频带能量收集的目的；2014年，刘颖等人研究了一阶、二阶传动低频压电振动发电装置，可有效降低装置的工作频率，其中，二阶传动梁在1 g条件下，可以获得10.98 Hz和44.52 Hz两个低频率的电压峰值[8]。通过前述的研究可以发现，仅当压电装置的固有频率与环境振动频率一致时，压电装置才能达到最好的发电效果，而实际环境振动的频率往往并不是固定的，因此，为提高压电振动发电装置在实际振动环境中的发电能力，压电装置还应具有一定的宽频工作能力。

本文针对单悬臂梁压电振动发电装置的一阶与二阶模态频率比较大的问题[17]，研究了一种两自由度宽频带悬臂梁压电发电装置，通过合理的设计结构参数，使压电发电装置的前两阶模态频率接近，达到了拓宽频带的目的。

2　两自由度悬臂梁压电发电装置频率特性模型的建立

两自由度宽频带悬臂梁压电发电装置的结构如图1所示，该压电振动发电装置主要由2个压电梁和2个质量块进行直线连接形成。为实现两自由度悬臂梁压电发电装置的宽频带发电，可通过合理的设计该装置的结构参数，使其一阶和二阶模态频率接近，以实现在压电发电装置的前两阶模态频率间形成宽频带发电能力的目的。

图1　两自由度悬臂梁压电发电结构示意图

为便于对两自由度悬臂梁压电发电装置的频带分析，假设压电梁1的长度为l1，宽度为b1，压电片厚度为tp1，金属弹性基片厚度为tc1；压电梁2的长度为l2，宽度为b2，压电片厚度为tp2，金属弹性基片厚度为tc2；质量块1的等效质量为m1，质量块2的等效质量为m2；压电梁1的等效刚度为k1，压电梁2的等效刚度为k2；Ep为压电片弹性模量，Ec为金属弹性基片弹性模量。

两自由度悬臂梁压电发电装置中压电梁的等效刚度与压电梁的尺寸参数之间的关系为：

(1)

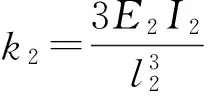
(2)

其中：E1I1和E2I2分别为两压电梁的截面等效刚度。

两自由度悬臂梁自由振动时可简化为两自由度弹簧-质量-阻尼系统，系统的动力学方程为：

(3)

令：

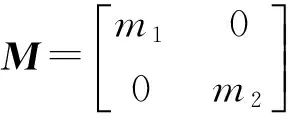
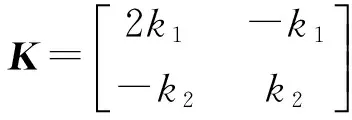
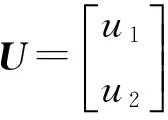
则系统的自由振动方程为：

(4)

由系统的特征方程可得：

(2k1-ω2m1)(k2-ω2m2)-k1k2=0.

(5)

系统的前两阶模态频率分别为：

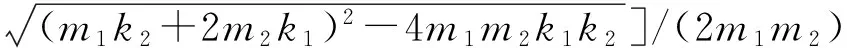
(6)

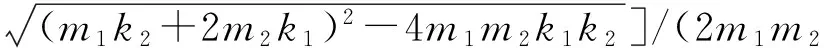
(7)

系统的前两阶模态频率之间的关系为：

(8)

可知，两自由度悬臂梁压电发电装置的前两阶模态频率与装置的尺寸及质量块的取值有关，通过合理的设计装置的结构参数，使得装置的前两阶模态频率最大限度的接近，从而起到频带拓宽的目的。

3　理论模型验证与数值模拟

3.1理论模型验证

为验证上述理论模型能否正确反映压电振动发电装置的频率特性，利用Ansys软件建立了两自由度悬臂梁压电发电装置的有限元仿真模型。有限元建模中，压电陶瓷材料选用PZT-5H，金属弹性基片材料选用铍青铜，质量块材料选用钢，相应的材料性能参数如表1所示。

表1　压电发电装置材料性能参数

另外，有限元模型中压电梁1和压电梁2的尺寸均相同，且其长度为30 mm，宽度为8 mm，压电陶瓷片厚度为0.4 mm，铍青铜厚度为0.6 mm；质量块1和质量块2的质量均为6.0 g。有限元仿真模型如图2所示。

图2　有限元仿真模型

根据上述有限元仿真模型，仿真得到两自由度悬臂梁压电发电装置的一阶模态频率为131.06 Hz，二阶模态频率为346.61 Hz。根据前述理论模型，计算得到装置的一阶模态频率为125.87 Hz，二阶模态频率为329.54 Hz。可以看出，理论计算结果与有限元仿真结果基本一致，验证了理论模型的可行性。

3.2数值模拟分析

为了直观的说明两自由度悬臂梁压电发电装置前两阶模态频率的比值与装置结构参数之间的影响关系，对前述理论模型进行了数值模拟分析。

图3所示为仅改变装置中压电梁1与压电梁2的长度比，其它参数保持不变的情况下，装置的前两阶模态频率的变化情况。显然，随着长度比的增大，装置的一阶模态频率和二阶模态频率不断减小，但是二阶模态频率的减小速度明显较快，且在长度比约为0.8时，装置的前两阶模态频率最接近。通过合理的优化装置的结构参数，可以使得装置的前两阶模态频率之间的距离最小，这样，就容易形成宽频带的能量收集。

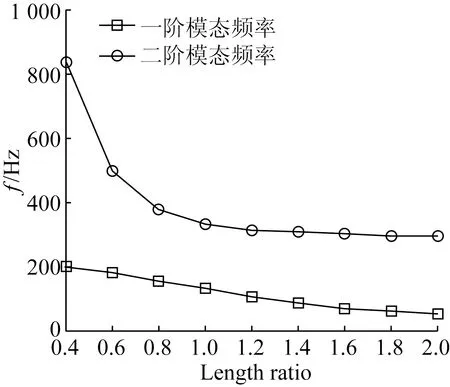
图3　频率与长度比关系曲线

图4所示为两自由度悬臂梁压电发电装置的前两阶模态频率比与压电梁1和压电梁2的长度比的关系曲线，随着长度比的增大，装置的前两阶模态频率比先减小后增大，即存在一个最小值，且在长度比近似为0.8时，装置的前两阶模态频率比最小。说明在两自由度悬臂梁压电发电装置的宽频带设计中，只要合理的设计压电梁1与压电梁2的长度比，即可使得装置的前两阶模态频率比最小，达到拓宽装置的工作频带的目的。

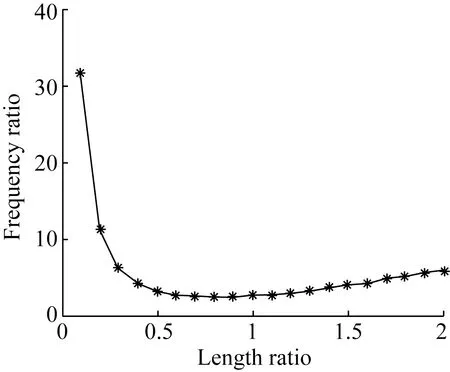
图4　频率比与长度比关系曲线

图5所示为两自由度悬臂梁压电发电装置的前两阶模态频率比与宽度比的关系曲线，在数值模拟中，仅改变装置中压电梁1与压电梁2的宽度比，其它参数保持不变。当宽度比近似为2.0时，装置的前两阶模态频率比最小。这说明，在两自由度悬臂梁压电发电装置的宽频带设计中，宽度比也是影响其频带宽度的一个重要因素。

图5　频率比与宽度比关系曲线

图6所示为两自由度悬臂梁压电发电装置的前两阶模态频率比随着压电梁中金属弹性基片与压电陶瓷片厚度比的关系曲线，其中，在厚度比的变化过程中，装置的其它结构参数保持不变。随着厚度比的增大，装置的前两阶模态频率比先减小后增大，且在厚度比为1.0时，装置的前两阶模态频率比最小。由此可见，为获得两自由度悬臂梁压电发电装置的宽频带能量收集，对于金属弹性基片与压电陶瓷片的厚度也应进行合理设计。

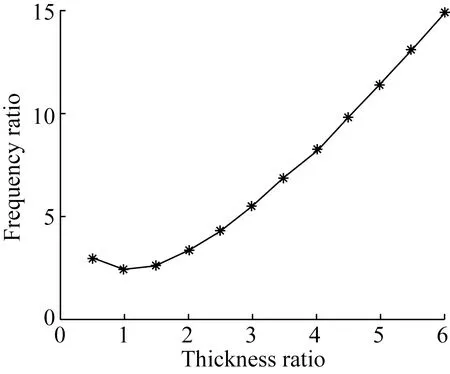
图6　频率比与厚度比关系曲线

图7所示为两自由度悬臂梁压电发电装置的前两阶模态频率比随着质量块的质量比的变化关系，在质量块1和质量块2质量的变化中，装置中压电梁的各尺寸参数均保持不变。随着两质量块质量比的增大，装置的前两阶模态频率比出现一个最小值，且在质量比为0.5时，装置的前两阶模态频率比最小。由此可知，为提高两自由度悬臂梁压电发电装置的宽频带发电能力，除了合理设计压电梁的尺寸参数之外，对于质量块的大小也应合理选择。

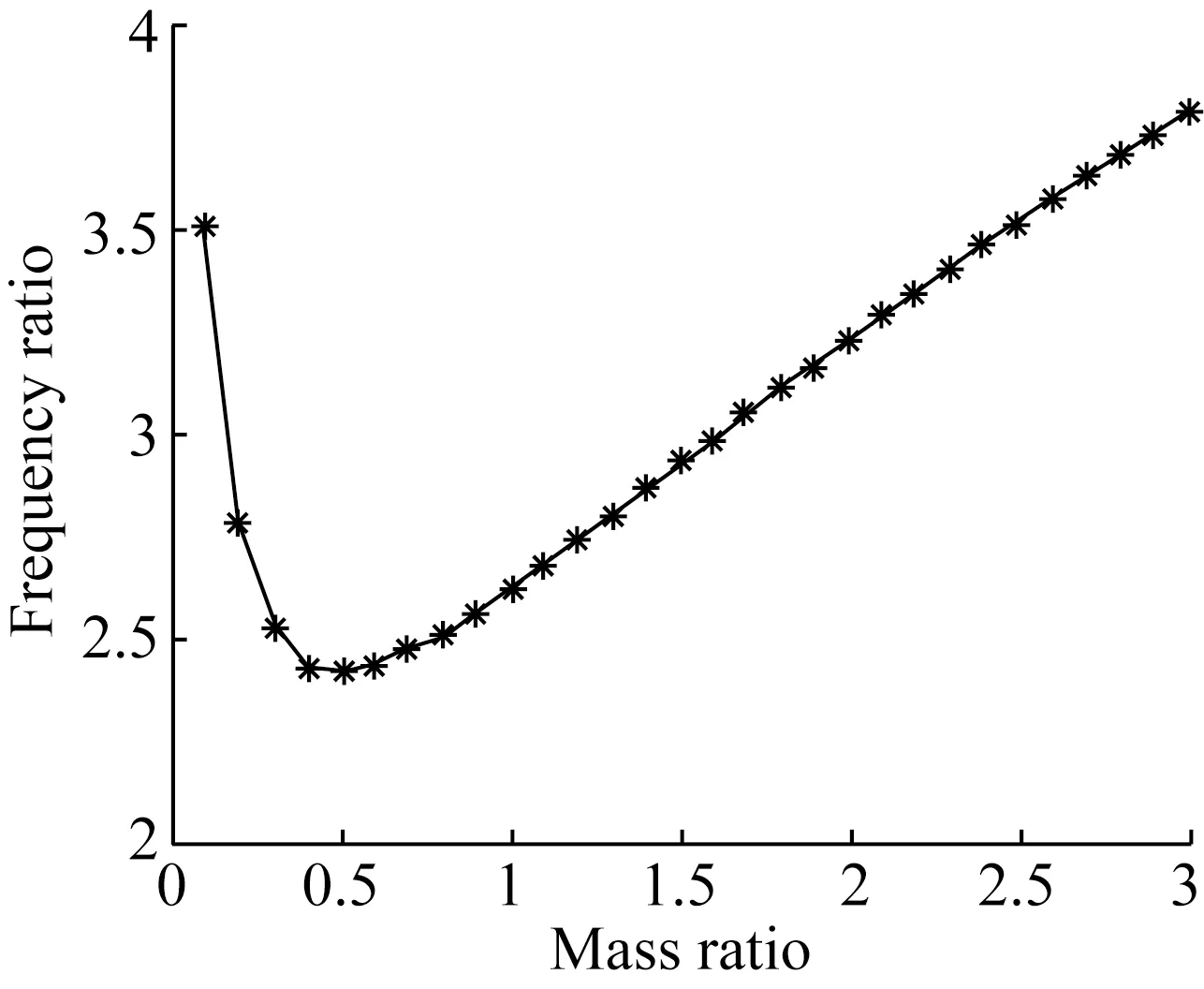
图7　频率比与质量块的质量比关系曲线

4两自由度悬臂梁压电发电装置幅

值响应特性分析

在两自由度悬臂梁压电发电装置幅值响应特性分析中，假设质量块2受到一竖直方向的力F0sinωt，则两自由度压电梁系统无阻尼受迫振动方程为：

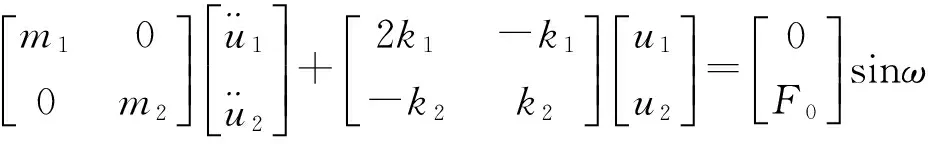
(9)

由式(9)可以得到：

(10)

其中：

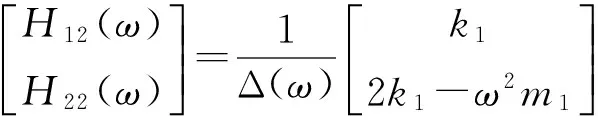
Δ(ω)=(2k1-ω2m1)(k2-ω2m2)-k1k2.

根据式(6)～(7)，可以得到：

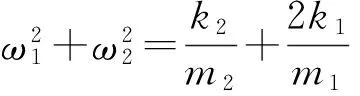
(11)

(12)

联立式(11)和(12)，可以解得压电梁1和压电梁2的幅值响应函数分别为：

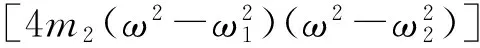
(13)

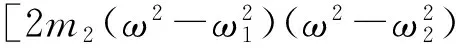
(14)

图8和图9所示分别为压电梁1和压电梁2末端幅值响应曲线的数值模拟结果，在外界激励频率接近于两自由度悬臂梁压电发电装置的前两阶模态频率时，装置中压电梁1的末端幅值和压电梁2的末端幅值分别达到最大，且装置的前两阶模态频率比为2.62，另外，也可看到，压电梁2的末端幅值在装置的一阶模态频率处明显大于压电梁1的末端幅值。

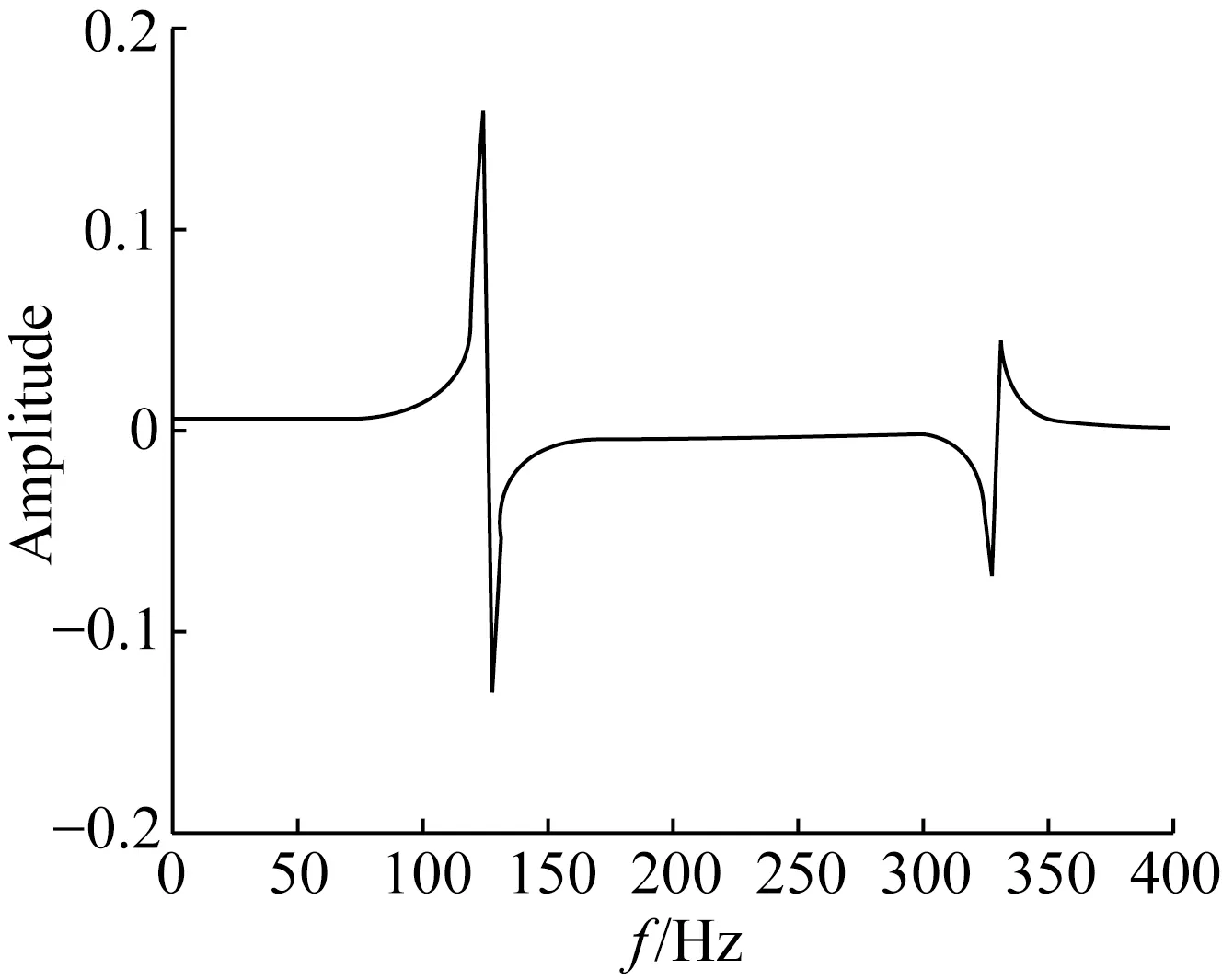
图8　压电梁1末端幅值响应

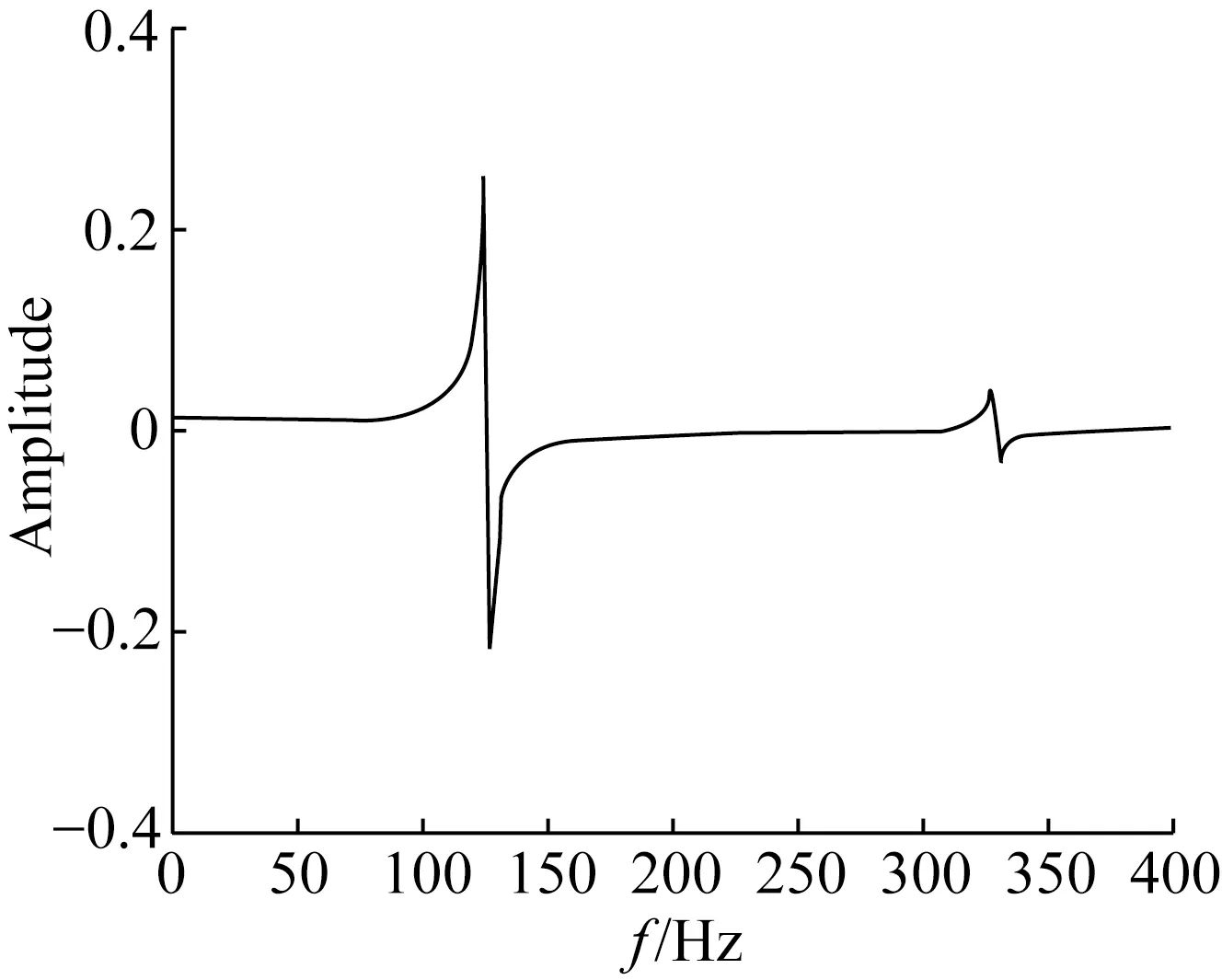
图9　压电梁2末端幅值响应

5　设计实例与试验测试

5.1设计实例

通过前述两自由度悬臂梁压电发电装置的频率特性理论模型及其数值模拟结果，可以得到，两自由度悬臂梁压电发电装置的前两阶模态频率取决于装置的尺寸参数，且存在最优的尺寸参数使得压电发电装置的前两阶模态频率最接近。

以前述理论分析的结果为依据，对宽频带的两自由度悬臂梁压电发电装置进行设计。考虑到各个尺寸参数对最优结果的耦合影响，显然无法直接根据以上数值模拟结果得到最优尺寸参数，而必须综合考虑各个尺寸参数的影响通过优化最终确定最优尺寸参数。为此，以压电梁1和压电梁2的长度l1和l2、宽度b1和b2、压电片厚度tp1和tp2、金属弹性基片厚度tc1和tc2、质量块1的等效质量m1、质量块2的等效质量m2为设计变量，以压电发电装置前两阶模态频率比最小为目标，建立目标函数：

ηω=minf(l1，b1，tp1，tc1，l2，b2，tp2，tc2，m1，m2).

(15)

其中，目标函数为：

f(l1，b1，tp1，tc1，l2，b2，tp2，tc2，m1，m2)=

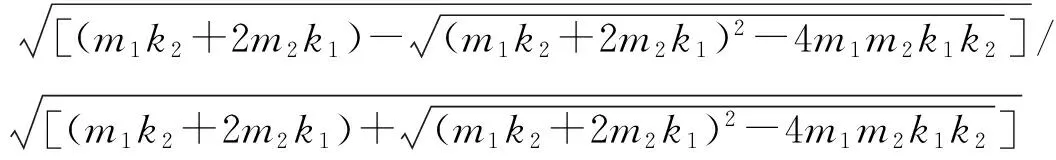
(16)

式中：

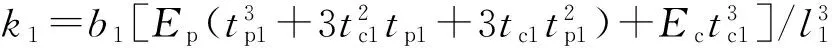
综合考虑压电发电装置的尺寸空间要求及压电陶瓷片材料的强度要求，同时假设压电片弯曲变形中受到的最大拉应力为σpzt，max，材料的抗拉强度为σpzt，th，则设置约束条件为：

10 mm≤l1≤40 mm，

5 mm≤b1≤20 mm，

0.3 mm≤tp1≤1 mm，

0.3 mm≤tc1≤1.5 mm，

10 mm≤l2≤40 mm，

5 mm≤b2≤20 mm，

0.3 mm≤tp2≤1 mm，

0.3 mm≤tc2≤1.5 mm，

1 g≤m1≤15 g，

1 g≤m2≤15 g，

σpzt，max≤σpzt，th.

采用序列二次规划法对压电发电装置的目标函数进行优化，给定初始优化参数如下：压电梁1的长度为30 mm，宽度为8 mm，压电片厚度为0.4 mm，金属弹性基片厚度为0.6 mm；压电梁2的尺寸参数与压电梁1相同；质量块1和质量块2的等效质量均为6 g。经过优化后获得最优的尺寸参数如下：压电梁1的长度为30 mm，宽度为8 mm，压电片厚度为0.4 mm，金属弹性基片厚度为0.4 mm；质量块1的等效质量为6 g；压电梁2的长度为33 mm，宽度为8.8 mm，压电片厚度为0.4 mm，金属弹性基片厚度为0.6 mm；质量块2的等效质量为6 g。

在上述设计参数下，根据式(8)，经过计算可以得到合理设计之后的两自由度悬臂梁压电发电装置的前两阶模态频率比为2.41，该数值明显小于前述仿真结果。

5.2试验测试

为进一步验证两自由度悬臂梁压电发电装置的宽频带性能，以上述合理设计之后的两自由度悬臂梁压电发电装置的设计参数和仿真模型的设计参数为例，试制了压电发电装置，并进行频率特性测试，试验测试照片如图10所示，试验测试中各压电陶瓷片进行电学串联。

图10　试验测试照片

图11　开路输出电压与频率关系曲线

试验测得压电发电装置的开路输出电压与频率的关系曲线如图11所示。可以看到，前述仿真模型的一阶与二阶模态频率分别为129 Hz和334 Hz，频率比为2.59，合理设计后压电发电装置的一阶与二阶模态频率分别为107 Hz和248 Hz，频率比为2.32，合理设计后压电发电装置的前两阶模态频率之间的距离明显缩小。文献[17]给出的单频悬臂梁的一阶与二阶模态频率比近似为6，显然，相比较单自由度悬臂梁压电发电装置，两自由度悬臂梁压电发电装置更容易在一阶与二阶模态频率间形成宽频带的能量收集。

6　结　论

本文以一种两自由度悬臂梁压电发电装置为对象，重点进行了其宽频带发电能力的研究。建立了两自由度悬臂梁压电发电装置的频率特性模型，通过该模型可知，装置的前两阶模态频率与装置的尺寸及质量块的取值有关。同时，对该理论模型并进行了有限元仿真验证。对两自由度悬臂梁压电发电装置的频率特性模型进行了数值模拟，可以发现，装置的前两阶模态频率比随着长度比、宽度比、厚度比及质量块的质量比的增大均出现一个最小值，且在长度比为0.8，宽度比为2.0，厚度比为1.0，质量块的质量比为0.5时，装置的前两阶模态频率比最小。在外界激励频率接近于两自由度悬臂梁压电发电装置的前两阶模态频率时，装置中压电梁1的末端幅值和压电梁2的末端幅值分别达到最大，且装置的前两阶模态频率比为2.62，同时，压电梁2的末端幅值在装置的一阶模态频率处明显大于压电梁1的末端幅值。实例设计了两自由度悬臂梁压电发电装置，并进行了试验测试，证实了优化后的两自由度悬臂梁压电发电装置更容易在一阶与二阶模态频率间形成宽频带的能量收集。

[1]DAI H L， ABDELKEFI A， WANG L. Theoretical modeling and nonlinear analysis of piezoelectric energy harvesting from vortex-induced vibrations [J].JournalofIntelligentMaterialSystemsandStructures， 2014， 25(14)： 1861-1874.

[2]ARRIETA A F， DELPERO T， BERGAMONI A E，etal.. Broadband vibration energy harvesting based on cantilevered piezoelectric bi-stable composites [J].AppliedPhysicsLetters， 2013， 102(17)： 173904.

[3]ROUNDY S， LELAND E S， BAKER J，etal.. Improving power output for vibration-based energy scavengers [J].IEEEPervasiveComputing， 2005， 4(1)： 28-36.

[4]SHAHRUZ S M. Design of mechanical band-pass filters with large frequency bands for energy scavenging [J].Mechatronics， 2006， 16(9)： 523-531.

[5]KIM H W， BATRA A， PRIYA S，etal.. Energy harvesting using a piezoelectric cymbal transducer in dynamic environment [J].JapaneseJournalofAppliedPhysics， 2004， 43(6)： 178-183.

[6]ERTURK A， RENNO J M， INMAN D J. Piezoelectric energy harvesting from a L-shaped beam-mass structure with an application to UAVs [J].Journalofintelligentmaterialsystemsandstructures， 2009， 20(5)： 529-544.

[7]FEENSTRAA J， GRANSTROMA J， SODANO H. Energy harvesting through a backpack employing a mechanically amplified piezoelectric stack [J].MechanicalSystemsandSignalProcessing， 2008， 22(3)： 721-734.

[8]刘颖， 王艳芬， 李刚， 等. MEMS低频压电振动能量采集器[J]. 光学 精密工程， 2014， 22(9)： 2476-2482.

LIU Y， WANG Y F， LI G，etal.. MEMS-based low-frequency piezoelectric vibration energy harvester [J].Opt.PrecisionEng.， 2014， 22(9)：2476-2482.(in Chinese)

[9]王淑云， 阚君武， 王鸿云， 等. 基于圆弧限位的压电发电装置[J]. 光学 精密工程， 2013， 21(2)： 342-348.

WANG SH Y， KAN J W， WANG H Y，etal.. Piezoelectric energy generator based on deflection-limiting circular arc [J].Opt.PrecisionEng.， 2013， 21(2)： 342-348.(in Chinese)

[10]阚君武， 王淑云， 彭少锋， 等. 多振子压电发电机的输出特性[J]. 光学 精密工程， 2011， 19(9)： 2108-2116.

KAN J W， WANG SH Y， PENG SH F，etal.. Output performance of piezoelectric generators with multi-vibrators [J].Opt.PrecisionEng.， 2011， 19(9)：2108-2116.(in Chinese)

[11]贺学锋， 杜志刚， 赵兴强， 等. 悬臂梁式压电振动能采集器的建模及实验验证[J]. 光学 精密工程， 2011， 19(8)： 1771-1778.HE X F， DU ZH G， ZHAO X Q，etal.. Modeling and experimental verification for cantilevered piezoelectric vibration energy harvester [J].Opt.PrecisionEng.， 2011， 19(8)： 1771-1778.(in Chinese)

[12]于慧慧， 温志渝， 温中泉， 等. 宽频带微型压电式振动发电机的设计[J]. 传感技术学报， 2010， 23(5)： 643-646.YU H H， WEN ZH Y， WEN ZH Q，etal.. The design of piezoelectric vibration based generator with wide bandwidth [J].ChineseJournalofSensorsandActuators， 2010， 23(5)： 643-646.(in Chinese)

[13]ARROYO E， BADEL A， FORMOSA F. Energy harvesting from ambient vibrations： electromagnetic device and synchronous extraction circuit [J].JournalofIntelligentMaterialSystemsandStructures， 2013， 24(16)： 2023-2035.

[14]CEPNIK C， YEATMAN E M， WALLRABE U. Effects of nonconstant coupling through nonlinear magnetics in electromagnetic vibration energy harvesters [J].JournalofIntelligentMaterialSystemsandStructures， 2012， 23(13)： 1533-1541.

[15]MITCHESON P D， MIAO P， STARK B H，etal.. MEMS electrostatic micropower generator for low frequency operation [J].SensorsandActuatorsA， 2004， 115(2-3)： 523-529.

[16]BAGINSKY I L， KOSTSOV E G， KAMISHLOV V F. Two-capacitor electrostatic microgenerators [J].Engineering， 2013， 5(11A)： 9-18.

[17]方同， 薛璞. 振动理论及应用[M]. 西安： 西北工业大学出版社， 1998.

FANG T， XUE P.Vibrationtheoryandapplication[M]. Xi’an： Northwestern Polytechnical University Press， 1998.(in Chinese)

刘祥建(1980-)，男，山东五莲人，博士，副教授，2012年于南京航空航天大学获得博士学位，主要从事振动能量收集技术方面的研究。E-mail： xiang jianliu@126.com

朱莉娅(1986-)，女，江苏徐州人，博士，讲师，2012年于南京航空航天大学获得博士学位，主要从事振动能量收集、三维打印等方面的研究。E-mail： julia_860527@163.com

(版权所有未经许可不得转载)

Broadband generation performance of two-degree-of-freedom cantilever beam piezoelectric generator

LIU Xiang-jian1， ZHU Li-ya2， CHEN Ren-wen3

(1.SchoolofMechanicalandElectricalEngineering，JinlingInstituteofTechnology，Nanjing211169，China；2.JiangsuKeyLaboratoryof3DPrintingEquipmentandManufacturing，NanjingNormalUniversity，Nanjing210042，China;3.StateKeyLaboratoryofMechanicsandControlofMechanicalStructures，NanjingUniversityofAeronauticsandAstronautics，Nanjing210016，China)

*Correspondingauthor，E-mail：xiangjianliu@126.com

A two-degree-of-freedom cantilever beam piezoelectric generator was explored to improve the generation performance of the cantilever beam piezoelectric generator under the variety of the ambient vibration energy sources. The theoretical model of the frequency characteristics of the two-degree-of-freedom cantilever beam piezoelectric generator was established and finite element analysis was performed for the proposed theoretical model. The theoretical results show that the theoretical analysis and finite element simulation are in agreement well. A numerical simulation was carried out for the frequency characteristic model of the two-degree-of-freedom cantilever beam piezoelectric generator and the results show that the ratio of the 1st modal frequency to the 2nd modal frequency will be a minimum value with the increase of the length ratio, width ratio, thickness ratio and the mass ratio, and the minimum value of the ratio of the 1st modal frequency to the 2nd modal frequency can be obtained at the length ratio of 0.8, width ratio of 2.0, thickness ratio of 1.0, and the mass ratio of 0.5. The results demonstrate that the frequency-band of the two-degree-of-freedom cantilever beam piezoelectric generator is expanded by optimizing the structure parameters to reduce the distance between the 1st modal frequency and the 2nd modal frequency. Finally, the two-degree-of-freedom cantilever beam piezoelectric generator was designed and the broadband generation performance of the generator verified.

piezoelectric generator; two-degree-of-freedom cantilever beam; broadband; frequency characteristics

2016-01-28；

2016-03-04.

国家自然科学基金项目(No.51305183)；江苏省高校自然科学研究面上项目(No.14KJB480004)；江苏省“青蓝工程”资助项目(No.2014)；金陵科技学院博士科研启动基金项目(No.jit-b-201412)

1004-924X(2016)07-1669-08

TN384；TM619

Adoi:10.3788/OPE.20162407.1669