离轴反射式光学系统结构随机振动响应与疲劳分析

吕　超， 孙安信，车　英，王加安

(长春理工大学 光电工程学院，吉林 长春 130022)



离轴反射式光学系统结构随机振动响应与疲劳分析

吕超， 孙安信，车英，王加安

(长春理工大学 光电工程学院，吉林 长春 130022)

为了探索振动环境对离轴反射式光学系统的影响，本文对其系统结构部分进行了随机振动响应分析以及疲劳分析。利用有限元软件MSC/Patran建立光学系统结构的整体模型并进行模态分析，以实际装配时基体框架前端连接法兰盘的连接孔部位作为边界条件，通过对其每个节点的六自由度进行约束并进行模态响应分析。分析结果表明在X、Y与Z三个方向上平移及旋转变化量均很小，满足空间环境中测量系统的精度要求。通过对光学结构整机部分在三个方向随机振动载荷作用下进行了有限元分析，结果表明光学结构内部最大应力分别为151、267和280 Mpa，都小于材料的抗拉强度，且有足够的安全阈度。根据所选的铝合金A709的 疲劳曲线,以及应力响应PSD谱，利用Palmgren-Miner假设，对本文所选定的光学结构及其主框架结构在动力学环境下进行疲劳分析，结果表明其满足系统使用要求。

离轴反射；光学系统结构;有限元分析;随机振动;疲劳分析

1　引　言

航空遥感测量技术日渐成熟，一般的光学系统已经不能满足使用者的要求。现设计出一种新型的离轴反射式光学系统结构，其具有小型化，轻量化等特点。在许多应用场合尤其是非常恶劣的应用环境下，光学系统会因外界环境产生随机的振动，从而发生面形变化及刚体位移，使成像效果变差，从而影响测量精度。因此，对离轴反射式光学系统结构部分进行随机振动的响应分析以及疲劳分析，观察光学系统结构整体对随机振动产生的变化并找到结构中容易疲劳损伤的位置，对于离轴反射光学系统的研究具有很大的意义[1-6]。

利用计算机对三维图进行有限元分析，模拟复杂的振动环境，从而直观的得到响应值以及容易疲劳损伤的位置，方便对系统结构进行改进和优化[7-9]。本文主要针对离轴反射式光学系统结构部分，利用有限元分析软件MSC/Nastran对其进行随机振动以及疲劳分析。通过有限元计算，研究了测量系统的光学结构部分经受此动力学环境的能力，得出了整机约束模态分析结果，找出了给定X，Y与Z方向上振动最大应力响应以及得到容易发生疲劳损伤的位置，并计算出发生疲劳破坏时的总循环次数，为离轴反射式光学系统结构部分设计以及提高振动环境下的抗过载能力提供了参考。

2　光学系统结构及有限元模型建立

2.1光学系统结构

由于需要同时在可见光与红外波段下进行探测工作，并结合系统的参数要求，设计出一种新型主系统采用RUG-TMA光学系统，包括主镜、次镜、三镜三块离轴非球面反射镜，在系统中增加折叠镜使光学系统结构更为紧凑，其光路设计图如图1所示。其成像原理是：来自无限远光线经过主镜反射后投射到次镜，再次反射到三境后，经过折叠镜反射后成像到像平面上。整机结构图如图2所示。

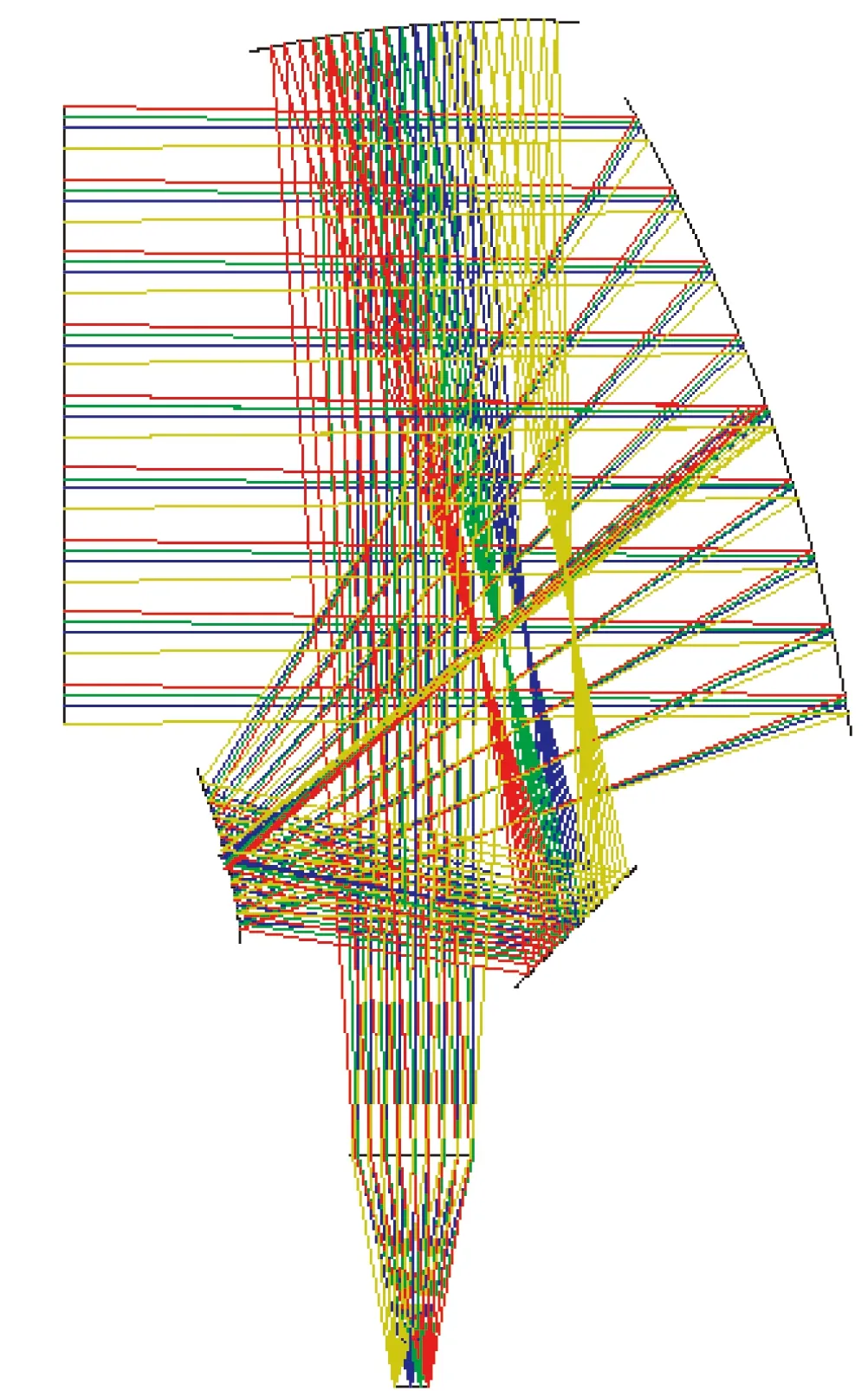
图1　光学系统设计光路图

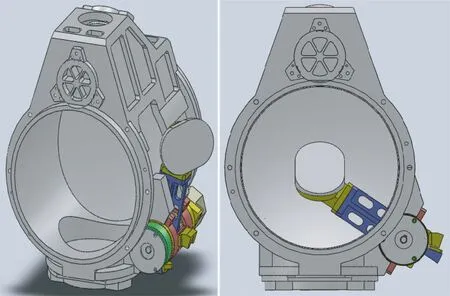
图2　光学系统整体结构图

2.2材料属性

正确选择光学系统结构的材料，不仅可以提高其中各反射镜支撑结构的比模数(材料的刚度与其质量的比值，亦作比刚度)，更可使其与反射镜的光学材料特性更加匹配，从而在各种环境条件下其力学和热尺寸稳定性得到显著提升[10]。本文综合考虑了光学系统结构设计和使用环境的特殊性，在整机结构材料的选择上，以低线胀、高强度、轻质材料为优选材料。经过对比和分析，同时确保光学系统结构中光学元件与机械结构都具有热变化的统一性以及较好的抗拉、抗振性能，最后选择以铝合金、钛合金及钢等作为该光学系统结构的主要材料。

2.3模型的建立

整机有限元模型采用MSC/Patran建模，MSC/Nastran求解，模型构造要严格按照该离轴反射式光学系统结构进行有限元建模，以保证有限元模型结构与本文所用的光学系统结构一致；在关键的力的传递路径上，网格划分要密集；在非关键部位，本着能量、刚度等效原则，可适当简化，但简化后的构件必须要有真实构件对整机的质量(蕴含惯量以及热容量)和刚度一样的贡献效果；框架结构复杂，采用TET10单元构造，其它所有零件全部采用六面体单元或五面体单元构造。最新整机结构的有限元模型如图3所示，其中节点总数为：74 055个，单元总数为：42 262个。

图3　整机的有限元模型

2.4边界条件

一般情况下，利用有限元软件对结构模型进行动力学分析时，主要考虑其线性特性，本文结合实际装配情况，以基体框架前端连接的法兰面的六个螺钉通孔部位作为结构的边界条件，对其节点的六个自由度进行全约束，得到的模型边界条件图如图4所示。

图4　模型的边界条件

3　模态与随机振动响应分析

3.1有限元模态分析对象、方法及步骤

根据该结构系统应用的工作环境，本文主要针对光学系统结构整体进行强度特性分析。强度特性分析包括随机振动应力响应分析和整机约束模态分析，模态分析即是以求出系统的模态参数为目的，利用各阶主振型所对应的模态坐标来代替其物理坐标，从而使微分方程组解耦，变成各自独立的微分方程[11]。

结构的模态是由其结构本身的特性所决定的，与其他条件无关，利用计算机将结构模型各个阶段的频率值以及特征向量进行计算，得出单独的振动系统模态参数(即各个模态下某一自由度方向上的响应量)，再统一进行线性分析和叠加计算，即可得到系统在谱激励下的响应[12]。

3.2模态分析结果

整机约束模态分析结果如表1所示。

表1　整机的前十阶约束模态及模态参与因子

由表1可以看出，光学结构整机通过有限元软件分析，在前10阶模态的固有频率下X、Y和Z轴三个方向的平移与旋转变化量是非常小的，说明光学系统整体的结构合理可靠。图5显示的是前3阶模态振型，可以看出外部结构变化不明显，只有摆镜部分发生相对明显变化，这是由于摆镜的材料与构造所引起的。但从摆镜实际工作作用及原理来看，这并不影响本光学系统结构的正常测量。

(a)第一阶

(b)第二阶

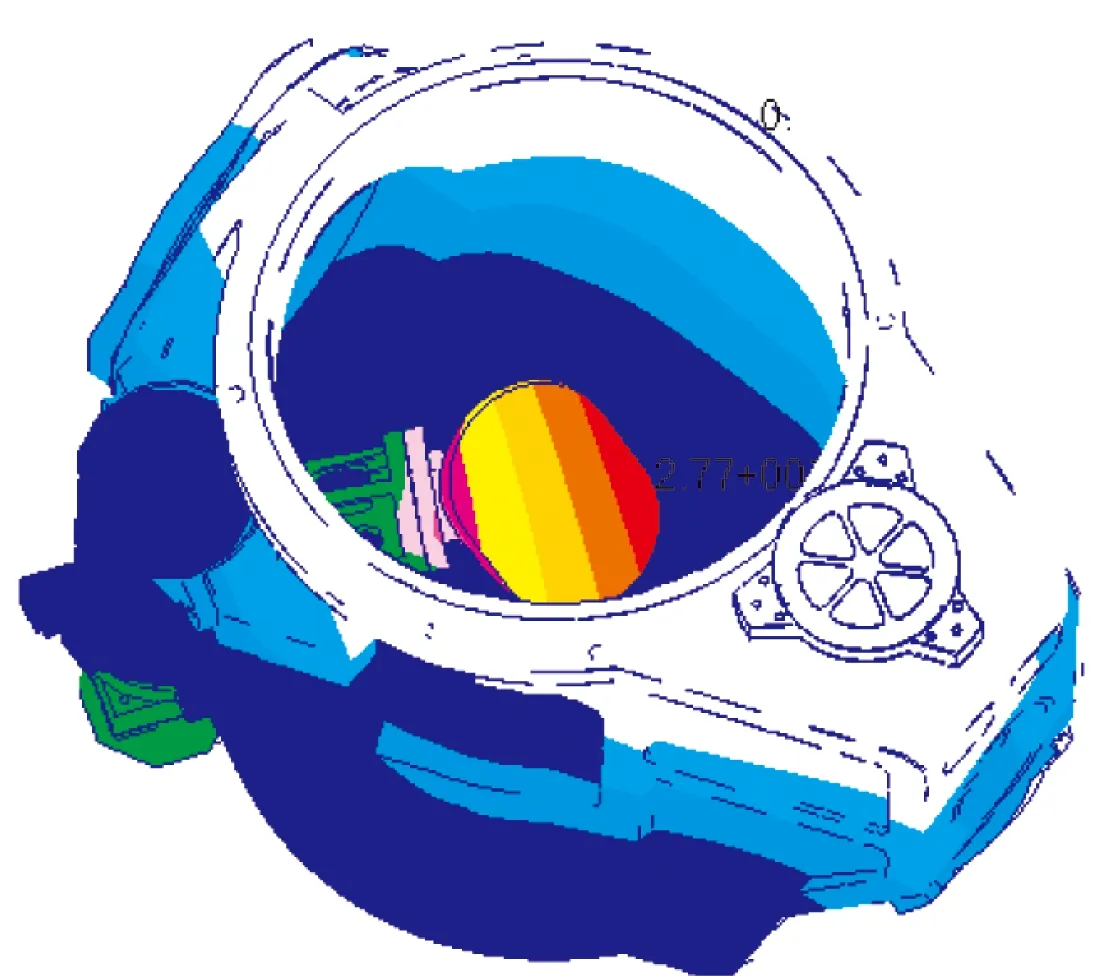
(c)第三阶

3.3有限元随机振动响应分析意义

航空遥感器在进行测量工作时难免会遇到气流、噪声等干扰，以及航空器在起飞、着落或进行特殊动作时，光学系统结构会在外界干扰下产生随机振动。该现象是一种不确定性的、无法用给定时间函数来描述的现象。其所受激励和其相应值无法确定，但可以利用数理统计的方法对其规律性进行研究[13]。在随机载荷作用下，对模型结构进行响应分析，当遇到自由度数目相对较大或系统模型结构较复杂时，一般选择利用计算机对数值进行数值计算分析，并将模态分析结果作为随机振动分析的基础数据。我们选用的随机振动响应分析法是用模态参数代替频率响应函数，将模态坐标下得到的响应值在几何坐标中表示，因此随机响应的模态分析法和频率响应的函数分析法是大同小异的[14]。

在随机激励载荷作用下，该光学系统结构的随机振动响应情况可以用其整机各重要部位的响应功率谱密度进行分析。因此，离轴反射式光学系统结构的随机响应分析不仅对其系统的结构可靠性有重要判定意义，同时对整个遥感器的研制也起了很大作用。

3.4随机振动应力响应分析结果

系统的阻尼对随机振动响应分析计算结果有很大的影响，由于阻尼的产生机理复杂，通常按被测系统的材料组成来设定阻尼比。本文中的光学系统结构绝大部分采用铝合金等金属材料制作，所以选择系统的阻尼比为5%，被测整机模型的实验条件如表2所示，

表2　随机振动试验条件

该光学系统结构的随机振动响应结果如图6和表3所示，由图6可以看出，在X、Y与Z三个方向施加随机振动载荷，整机发生疲劳损伤最明显位置均在基体框架前端连接的法兰面的六个螺钉通孔部位，此位置是整机模型边界约束位置。

(b) Y方向应力分布

(c) Z方向应力分布

最大应力安全阈度X向加载1513.2Y向加载2671.8Z向加载2801.75

在航空标准中，安全阈度大于零即可满足使用要求，根据应力云图所表示结果可以看出：该光学系统结构的各方向最大应力以及其安全阈度值远远满足了航空遥感工作的使用要求。

4　光学系统结构疲劳分析

结构的疲劳分析涉及了结构振动、结构动力学以及结构疲劳等多个学科。振动疲劳的问题在实际的工程分析中广泛存在，但是有关振动疲劳的研究仍处于初级阶段。根据实际载荷以及频率响应的特点所给出振动疲劳的定义为：振动疲劳是指结构在振动载荷作用下引起结构的动力学响应，从而导致结构的疲劳破坏[15]。

振动疲劳的响应为典型的随机过程，与一般的循环疲劳不同，若采用现有的疲劳寿命估算方法将不能准确的进行结构的振动疲劳寿命预测。结构的振动疲劳寿命分析必须先要进行振动载荷作用下的结构动力学响应分析，然后再基于动力学响应分析结果进行结构的振动疲劳寿命估算[16]。金属材料会存在一种理论的疲劳极限Sae，当应力小于该理论疲劳极限Sae时，材料便不会产生疲劳损伤，此时看以认为该结构的疲劳寿命为无穷大；当应力等于该材料的抗拉强度时，该结构的疲劳寿命为N=1/4。为了考虑抗拉强度与理论疲劳极限Sae对疲劳S-N曲线的影响，给出了S-N曲线的描述模型：

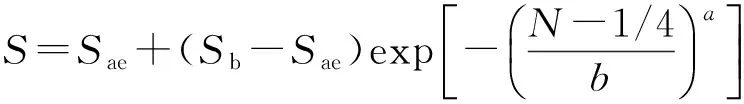
(1)

式中a和b为材料常数。图7为本文所选用的铝合金A709的S-N疲劳曲线。

图7　铝合金A709的S-N疲劳曲线

结构频域疲劳寿命估算方法是在频域内用谱参数描述响应的幅值信息，结合材料的疲劳寿命曲线和疲劳累积损伤理论进行寿命估算。频域法具有思路简单和计算量小等特点，受到学术界和工程界的重视。根据Palmgren-Miner累计损伤理论，累积损伤率为：

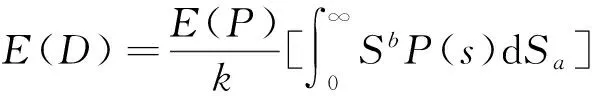
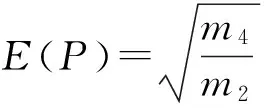
(2)

式中：G(f)为应力功率谱密度函数G(f)，k、b为材料S-N曲线中确定的材料常数。

(3)

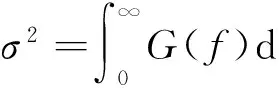
对宽带随机振动，应力峰值概率密度函数服从正态分布，由于E(0)与E(P)不等，峰值PDF不等于应力振幅PDF。为考虑局部峰值对结构疲劳寿命的影响，根据不同 PSD形状进行修正，获得了适用于宽带随机振动的寿命估算公式：

NT=E(0)/λE(D)，

(4)

其中：

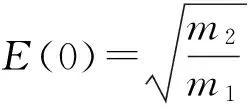
λ=αs+[1-as](1-α)bs，

as=0.926-0.033b，

bs=1.587m-2.323.

(5)

式中：m为材料参数，α为不规则因子 。

提取Z方向应力最大相应位置的单元Von Mise应力响应PSD谱如图8，结合材料的S-N曲线进行疲劳寿命估算，由公式(4)可得构件发生疲劳破坏时，总循环次数为6.67×106。

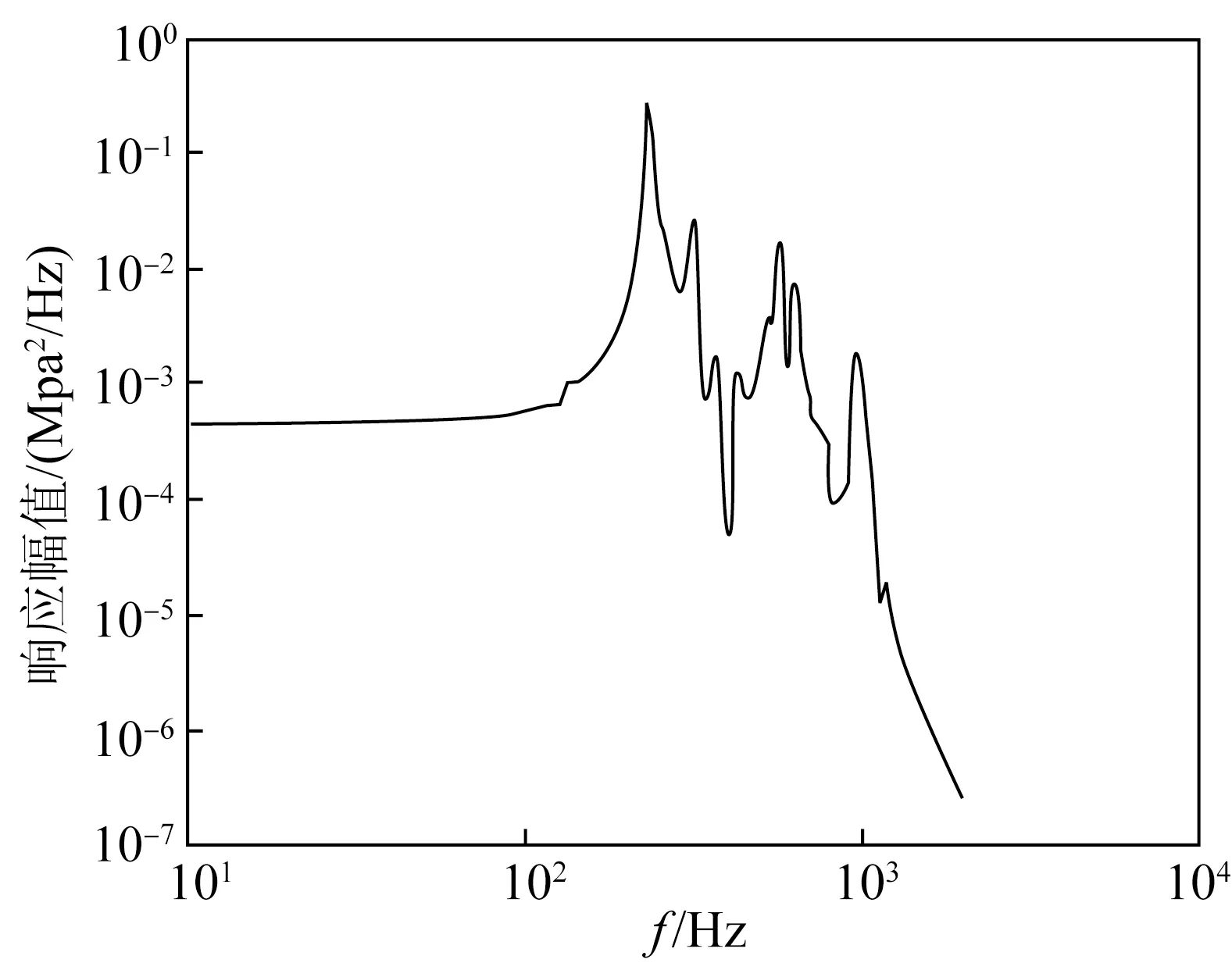
图8　应力响应PSD谱

其他疲劳损伤较为明显处皆为该模型零件连接处，说明该模型结构设计稳定性很好。从系统的模态分析和随机振动响应分析中可看出，本文所给出的离轴反射式光学系统结构部分产生较大加速度响应的频率是该系统的前几阶模态的谐振频率。为了减少外界振动环境对本系统的影响，同时考虑其使用环境的工作要求，在不增加整机质量的前提下可以采用零件整体化的方法，减少零件数量的同时也避免了零件过多造成振动产生的刚体变形，可以提高本系统的抗振性。

5　结论

本文利用有限元软件，对离轴反射式光学系统结构部分建立了有限元模型并进行了模态分析，分析结果表明在模态的固有频率下，模型在X、Y与Z轴三个方向的变化量都控制在很小范围内，说明了该系统结构的具有良好稳定性。完成了X、Y和Z轴三个方向激励下光学结构整机的随机振动响应，分析结果表明，在三个方向随机振动载荷作用下，整机结构内部最大应力分别为151、267和280 Mpa，都小于材料的抗拉强度，且有足够的安全阈度；同时指出了光学系统结构中，容易发生疲劳损伤的位置。针对应力最大位置进行了疲劳分析，分析结果显示构件发生疲劳破坏时，总循环次数为6.67×106，并提出了优化方案，对该离轴反射式光学系统结构的改进具有重要的理论与现实意义。

[1]李东.机载激光雷达三维成像技术研究[D].成都：电子科技大学，2012.

LI D.Airbornelaserradar3-Dimagingtechnologyresearch[D].Chengdu: University of Electronic Science and Technology of China,2012.(in Chinese)

[2]廖俊.基于正交分解的随机振动响应分析与随机载荷识别研究[D].哈尔滨：哈尔滨工业大学，2011.

LIAO J.Researchonresponseanalysisofstructurerandomvibrationandrandomloadingidentificationbasedonorthogonaldecomposition[D].Harbin: Harbin Institute of Technology,2011.(in Chinese)

[3]付密果，刘源，崔敏亮，等. 空间飞行器用金属橡胶减振器[J].光学 精密工程，2013,21(5):1174-1182.

FU M G, LIU Y, CUI M L，etal..Metal-rubber vibration absorber for aerocraft[J].Opt.PrecisionEng., 2013,21(5):1174-1182(in Chinese)

[4]徐红，关英俊. 空间相机1M口径反射镜组件结构设计[J].光学 精密工程，2013,21(6):1488-1495.

XU H, GUAN Y J. Structural design of 1M diameter space mirror component of apace camera[J].Opt.PrecisionEng., 2013,21(6):1488-1495.(in Chinese)

[5]刘强，何欣，谭进国，等.离轴四反光学系统反射镜支撑技术研究[J].光学技术，2010,36(4):489-494.

LIU Q,HE X,TAN J G,etal.. Investigation on mirror supporting structure of four-mirror reflective anastigmat optic system[J].OpticalTechnique， 2010,36(4):489-494.(in Chinese)

[6]丁学专,王 欣,兰卫华，等.离轴四反射镜光学系统设计[J].红外与激光工程,2008,37(2):319-321.

DING X Z,WANG X,LAN W H，etal.. Design of four-mirror reflective anastigmat optic system[J].InfraredandLaserEngineering， 2008,37(2):319-321.(in Chinese)

[7]韩昌元. 光电成像系统的性能优化[J].光学 精密工程，2015,23(1):1-9.

HAN C Y. Performance optimization of electro-optical imaging systems[J].Opt.PrecisionEng., 2015,23(1):1-9.(in Chinese)

[8]李宗轩. 主反射镜组件柔性环节随机振动响应分析与试验[J].红外与激光工程，2014,43(12)101-107.

LI Z X. Analysis and test on the response of primary mirror flexure under random vibration[J].InfraredandLaserEngineering， 2014,43(12)101-107.(in Chinese)

[9]钱庆，彭迪.某雷达有源安装板随机振动分析与试验研究[J].机械工程与自动化，2014,1(2)：12-14.

QIAN Q,PENG D. Random vibration analysis and experiment of active fixing-board of radar[J].MechanicalEngineering&Aotomation， 2014,1(2)12-14.(in Chinese)

[10]伞兵.空间光学遥感器小型反射镜组件结构设计与研究[D].长春：吉林大学，2014.

SAN B.Designandresearchonminitypereflectorassembliesinspaceopticalremotesensor[D].Changchun: Jilin University,2014.(in Chinese)

[11]张令弥.动态测试技术的发展系列讲座[J].振动与冲击，1998,17(3)：83-85.ZHANG L M. The development of the dynamic testing technology lecture series [J].JournalofVibrationandShock, 1998,3(17)：83-85.(in Chinese)

[12]于旭东，龙兴武，汤建勋.机械抖动激光陀螺的随机振动响应分析[J].光学 精密工程，2007,15(11):1760-1766.

YU X D,LONG X W,TANG J X. Random vibration analysis of mechanically dithered ring laser gyroscope [J].Opt.PrecisionEng., 2007,15(11):1760-1766.(in Chinese)

[13]徐昭鑫.随机振动[M].北京：高等教育出版社，1990.

XU S X.RandomVibration[M].Beijing: Higher Education Press,1990.(in Chinese)

[14]陈施能.某型航空电子设备及安装架动力学分析[D].成都：电子科技大学，2007.

CHENG S N.Acertaintypeofavionicsandinstallationrackdynamicsanalysis[D].Chengdu: University of Electronic Science and Technology of China,2007.(in Chinese)

[15]王明珠.结构振动疲劳寿命分析方法研究[D].南京：南京航天航空大学，2009.

WANG M Z.Researchonlifeanalysismethodforstructurevibrationfatigue[D].Nanjing: Nanjing University of Aeronautics and Astronautics The Graduate School,2009. (in Chinese)

[16]刘龙涛，李传日，程祺，等. 某结构件的随机振动疲劳分析[J]. 振动与冲击,2013,32(21)：97-101.

LIU L T,LI C R,CHENG Q，etal.. Random vibration fatigue analysis for a structure[J].JournalofVibrationandShock, 2013,32(21)：97-101. (in Chinese)

吕超(1989-)，男，吉林长春人，博士研究生，2011年于长春理工大学获得学士学位，主要从事精密测控技术与仪器方面的研究。E-mail：lcalcjou@sina.com

车英(1964-)，男，吉林长春人，教授，博士生导师，1987年于长春理工大学获得学士学位，1990年于长春理工大学获得硕士学位，2011年于长春理工大学获得博士学位，主要从事精密测控技术与仪器方面的研究。E-mail：cheying@cust.edu.cn

(版权所有未经许可不得转载)

Random vibration and fatigue analysis of off-axis reflective optical system structures

LÜ Chao， SUN An-xin， CHE Ying， WANG Jia-an

(CollegeofPhotoelectricalEngineering，ChangchunUniversityofScienceandTechnology，Changchun130022China)

*Correspondingauthor，E-mail：cheying@cust.edu.cn

In order to research the performance of off-axis reflective optical system against the dynamic environment, the random vibration and fatigue analysis is presented. The finite element model of optical system structures is established and its modal analysis is performed by the finite element software MSC/Patran. The boundary conditions are used as the connecting hole of the base frame which in the actual assembly. The analysis results are obtained by constraint to the each node, and it shows that the change of translation and rotation in three directions are very small. Content the accuracy requirement of the measurement system in the space environment. Finite element analysis of the optical system is carried out in the three directions random vibration load. The results show that the maximum stress of the optical system internal structure are 151, 267 and 280, respectively. According to theS-Nfatigue curve with aluminum alloy A709，and the PSD Spectrum of stress response，made the fatigue analysis of off-axis reflective optical system against the dynamic environment with Palmgren-Miner assumption，the results meet the system requirements.

off-axis reflective; optical system structure; finite element analysis; random vibration; fatigue analysis

2016-02-15；

2016-03-10.

长春理工大学基金资助(No.HKJ2013006)

1004-924X(2016)07-1661-08

V248.9；V391.9

Adoi:10.3788/OPE.20162407.1661