产品几何规范中非理想表面的多尺度表征

石照耀，姜海洋，张　敏

(北京工业大学 北京市精密测控技术与仪器工程技术研究中心，北京 100124)



产品几何规范中非理想表面的多尺度表征

石照耀，姜海洋，张敏

(北京工业大学 北京市精密测控技术与仪器工程技术研究中心，北京 100124)

考虑目前多数计算机辅助公差工具仅能针对具有理想几何表面的CAD模型，无法从物理几何角度真正反映制造误差，本文研究了非理想表面的多尺度表征，提出了一种能够表征产品表面及其截面轮廓宏观及微观多尺度形貌误差的非理想表面模型。首先，提出了一种利用离散小波实现形貌误差多尺度仿真的方法；其次，针对实际工件，利用离散小波对其表面及截面轮廓采样数据进行形貌误差多尺度仿真；最后，对形貌误差各尺度成分进行合成，得到具有多尺度形貌误差成分的工件三维表面及其二维截面轮廓的非理想表面模型。仿真及实验结果表明：利用提出方法可以实现具有多尺度形貌误差的非理想表面模型表征；仿真所得粗糙度Ra值与白光干涉仪测量所得值的平均相对误差不超过4%。得到的结果证明了提出方法的正确性和可行性，为更加全面地表征产品的非理想表面模型提供了有效途径。

产品几何技术规范；非理想表面模型；离散几何；小波分析；多尺度表征

1　引　言

几何公差用于控制零件几何要素的形状、方向、位置与其设计值的偏差[1-2]。目前，大多数计算机辅助公差工具可以帮助设计者实现公差规范，但是其研究对象仅针对具有理想几何表面的CAD模型，不能从物理几何角度真正反映制造误差，且缺少对于产品几何量变化的控制能力，不利于公差信息在整个产品生命周期的传递，也不利于计算机集成制造技术在现代制造业中的有效利用。同时，由于通用商业CAD软件的局限性，公差信息仅以文本信息形式存在于计算机中，不利于产品信息的数字化传递，这些都阻碍了公差信息在产品设计、制造及检验过程中的有效应用。

针对上述问题，Mathieu和Ballu提出了用于产品规范的GeoSpelling模型，该模型通过基于非理想表面模型的一系列概念和操作算子可实现公差在计算机中的表达及计算机辅助公差设计[3-4]。法国LURPA课题组对非理想表面模型[5]进行了一系列研究，张敏等[6-7]率先提出了利用离散几何算法实现非理想表面模型的建模仿真方法，以及针对基本零件曲面类型的形位公差的仿真算法，实现了GD&T与非理想几何形状模型的信息集成，对非理想表面模型的表征及仿真研究进行了初步探索。Schleich等[8]在张敏研究工作的基础上，提出了非理想表面模型表征的综合建模框架，对非理想表面模型的仿真与表征进行了完善，并成功应用于具有高副转动机构的公差分析中。上述关于非理想表面模型表征的研究均将制造误差划分为系统误差和随机误差来进行仿真分析，虽然能够表征出工件宏观的尺寸及形位公差变化信息，但无法描绘其微观表面形貌误差信息。因此，本研究提出一种能够反映产品加工表面宏观及微观多尺度形貌误差的非理想表面模型的表征和仿真方法，对于公差的数学模型以数据结构的存储形式有机集成到计算机系统中具有重要作用。

本文以新一代产品几何技术规范(GPS)为基础，以GeoSpelling模型为对象，以真实测量所获得的离散点云数据为切入点，通过离散几何及小波分析等现代工具，研究了一种可表征产品表面及其截面轮廓宏观及微观多尺度形貌误差的非理想表面模型的离散数据模型建模方法，可解决产品在设计、制造、检验过程中规范表达统一的难题，从而实现新一代GPS标准中规范与认证的对偶性要求。

2　形貌误差多尺度表征方法

非理想表面模型能够在物理几何角度真正反映制造误差信息，是对于物体真实形状的表征[3]，所以在构造非理想表面模型时要充分考虑研究物体真实形状的多尺度形貌误差。对于任意工件的加工表面，其表面形貌均可划分为宏观和微观，包括形状误差、波纹度以及粗糙度等多尺度形貌误差成分[9-12]。所以，为了获得含有宏观和微观形貌误差成分的非理想表面模型，针对上述3种尺度的形貌误差成分进行仿真分析以实现其误差表征。

2.1离散小波变换原理

为了实现3种尺度形貌误差成分的表征，首先要选择一种能够准确提取出多尺度误差成分的方法。目前，传统的滤波技术大多基于傅里叶变换，这种方法是将表面信号看做不同频率正弦波的线性叠加[13]。在几何产品表面成分分析过程中，对于高频信号和低频信号的分析宜分别采用小时间窗和大时间窗。然而，这种变时间窗的要求是时间窗固定的傅里叶变换无法满足的，其时域定位精度有限，无法实现时频同时定位。

基于傅里叶变换的上述局限性，20世纪80年代小波分析理论逐渐兴起。小波分析具有多尺度分析的特点，在时域和频域都有表征信号局部信息的能力，时间窗和频率窗都可以根据信号的具体形态进行动态调整。基于这些特点小波分析可以探测正常信号中的瞬态成分并展示其频率成分，具有对信号同时进行空间和频率定位的能力，能够实现表面信号多尺度频率成分的提取。因此，采用小波分析作为提取并表征产品表面及其截面轮廓多尺度形貌误差的方法。离散后的小波基函数在理想情况下满足正交完备性条件，此时计算出的小波变换系数无任何冗余度，可以最大限度地压缩数据并减小计算量。因此，采用离散小波变换对表面形貌采样数据进行多尺度滤波处理，可以解决同时表达微观和宏观表面数据量大的问题。

2.2轮廓误差小波模型

假设产品表面的截面轮廓为p(x)，将p(x)看作一维信号的离散采样点，且假设p(x)为所能获得的粗糙表面最精细的综合形貌，是包括表面形状误差、波纹度以及粗糙度的多尺度频率成分，频率为ω0～ω3。则有如图1所示形状误差f(x)对应低频成分[ω0，ω1]，波纹度w(x)对应带通成分[ω1，ω2]，粗糙度r(x)对应高频成分[ω2，ω3]，相应数学模型为：

p(x)=f(x)=w(x)+r(x).

(1)

图1　形貌误差成分频带分布

根据多尺度分析的Mallat算法，原始截面轮廓信号p(x)经过在尺度空间的j次分解后被分解为子集aj和dj，分别代表轮廓信号中的低频和高频成分在尺度2-j上的信息。p(x)分解后得到的小波分析结果为[15]：

Wj[p(x)]=(a1，d1)=(a2,d1,d2)=…=

(aj，d1，…，dk，…，dj).

(2)

2.3小波基选取

采用小波分析方法对截面轮廓形貌误差进行分析，首先要对其在不同尺度上进行分解，然后通过重构获得所需要的3种不同尺度的误差成分信息。由于小波分析的基函数具有不唯一性，采用不同小波基对同一产品表面进行分析时获得的误差成分信息结果相差甚远[15]，因此对于小波基的选取至关重要。

典型的正交小波基有Haar小波、Symlets小波、Coiflets小波及Daubechies小波，正交小波具有相同的分解和重构尺度及小波函数。然而，当这二者对应相同时，线性相位和完全重构条件不可兼得[13]。双正交小波分解与重构的小波尺度函数并不相同，因此这里选择双正交小波基，在可以实现完全重构的条件下获取线性相位，从而实现对于表面信号在时域及频域上的准确提取，进而实现表面特征的多尺度表征。此外，在传输特性上双正交小波基具有平滑的截止特性，且低通幅频特性接近水平，不存在过冲现象，故适合分析表面形貌信号[16]。

2.4频率成分划分

因为二维轮廓各尺度的形貌误差成分的主要区别在于所处的频率带不同，所以可以通过带通滤波器将其区分开。其中，尺度系数aj代表低频带[ω0，ω1]的信息，即形状误差；dk+1，…，dj，代表频率带[ω1，ω2]的信息，即波纹度；小波系数d1，…，dk，代表高频带[ω2，ω3]的信息，即粗糙度。其中，ω1=1/λf，λf为波纹度成分的频率下限；ω2=1/λc，λc为粗糙度成分的频率下限(粗糙度截止频率)；ω3=1/λs，λs为采样间隔决定的频率上限[17]，如图2所示。

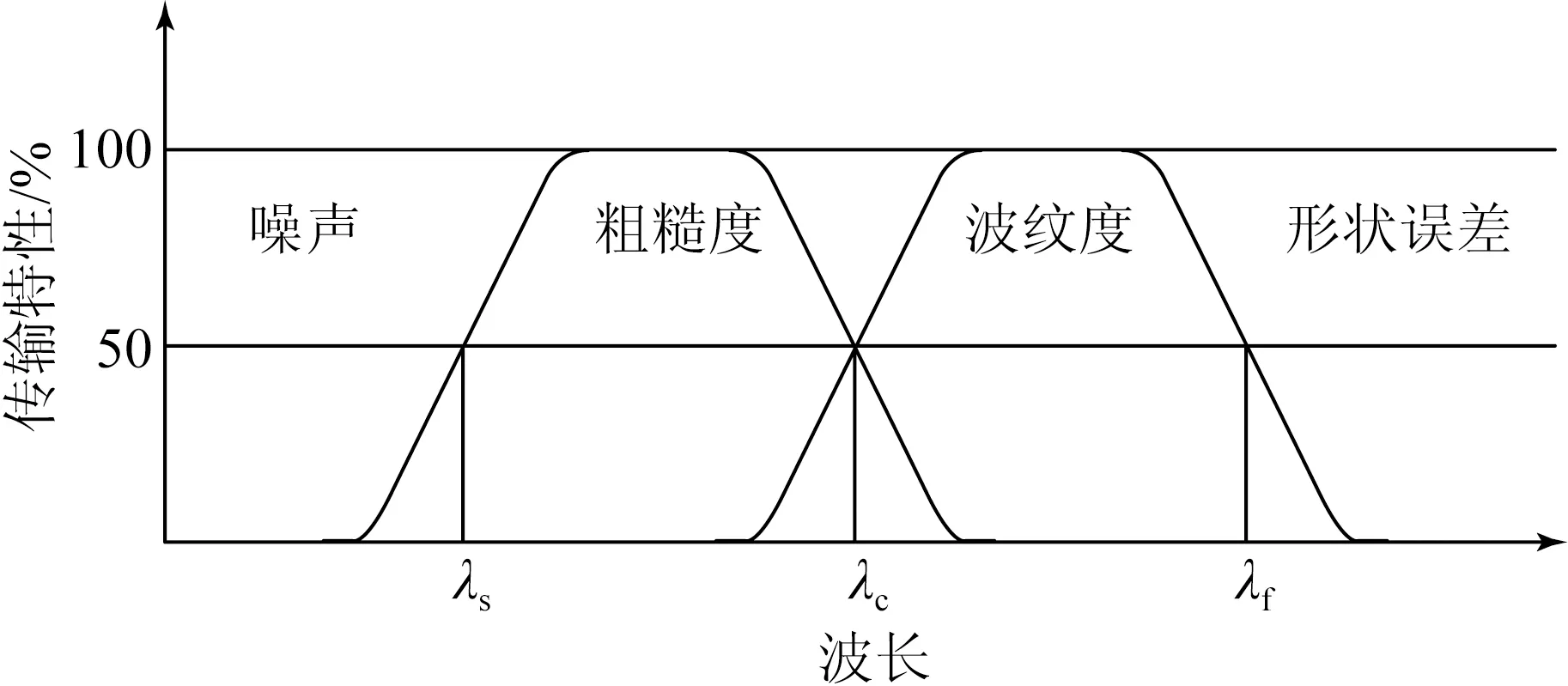
图2　形貌误差成分传输特性

形状误差：f(x)=IW(aj)=aj(x)-μ[dj(x)]

(3)

3　形貌误差多尺度表征方法验证

3.1仿真验证

(4)

利用离散小波对p(n)进行多尺度分解及重构，得到如图3所示仿真效果图。其中，采样点数为10 000个，采样间隔为1，其中横坐标表示采样点数，纵坐标表示模拟信号的幅值，单位为微米。由图中的仿真结果可以看出，离散小波变换可以成功地分离出不同尺度的正弦波信号和轮廓误差信号。

图3　轮廓形貌误差多尺度仿真

3.2实验验证

为了验证提出的方法可以应用在基于实测离散点云数据的形貌误差成分表征中，采用如图4所示的Talysurf CCI系列白光干涉仪(WLI)对实验工件表面形貌进行测量。

利用Talymap软件对测量区域沿y轴方向进行8次不重复随机轮廓截取，获得8组不同的产品截面轮廓离散采样数据及Ra值。其中，白光干涉仪每次取样区域为0.847 76 mm×0.847 84 mm，截取后的表面轮廓沿x轴方向取样长度为lr=0.847 76 mm，采样点数为1 024个，采样间距为0.828 7 μm。由于加工表面不均匀，故在实际评定表面粗糙度时取评定长度为 5lr[18]，获得4.27 mm×4.27 mm的评定区域。如图5所示为利用Matlab软件对实测离散点云数据进行处理所得到的评定区域表面形貌仿真结果，其中箭头所示方向为轮廓截取方向，为了使仿真结果能够更加清晰地表现，采用红、蓝两色反映高度极值，红色表示极大值，蓝色表示极小值。

图5　基于实测数据的表面形貌仿真

Fig.5Surface topography simulation based on actual measurement data

表1所示为8组轮廓数据经Talymap软件进行高斯滤波后获得的粗糙度值与本方法所获得的粗糙度值的比较。通过分析表1中数据发现各组误差均在允许范围内，平均相对误差值小于4%。因此，所提出的方法可以有效实现基于实测离散点云数据的多尺度轮廓形貌误差成分表征。

表1白光干涉仪实测与仿真所得粗糙度值比对

Tab.1Comparison for WLI measurement roughness and simulation roughness

序数测量值/μm仿真值/μm相对误差值/%10.501140.49191.84420.584690.59722.14030.475030.47990.33140.438970.41615.21050.548990.49859.19760.467360.50006.98470.541930.54230.06880.464380.44105.035

4　非理想表面模型建模实例

新一代GPS标准中的非理想表面模型是设计者头脑中想象的能够反映产品功能要求且考虑了加工误差的几何模型[3]。图6所示为实现具有宏观及微观多尺度形貌误差成分的非理想表面模型表征的整体设计思路。

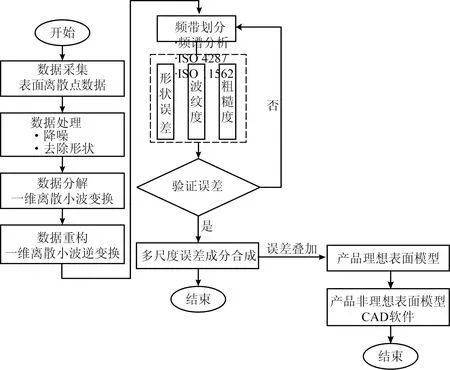
图6　生成非理想表面模型的过程

为了准确获得二维轮廓的非理想表面模型，选择表1中相对误差值最小的第7组数据进行多尺度轮廓形貌误差成分的提取及表征。图7所示为基于第7组数据利用Matlab仿真得到的截面轮廓，图中横坐标为采样点序数，纵坐标为采样点高度值，单位为μm。

图7　截面轮廓仿真

假设n为测量工件表面形貌时测量区域内某一截面轮廓上的采样点数，则在进行小波变换时依据最大理论尺度有：

j=[lbn].

(5)

则表面最多能进行j次小波分解。为了使采样结果更加稳定、准确，故取原始轮廓数据上第2 049至3 072个采样点，总计1 024个采样点进行多尺度误差成分的分离及提取。根据式(5)可知，采样信号最多可进行10次小波分解。然而，当分解到第10层时仅剩下1个采样点，以1个点代替一条轮廓曲线是不合理的，所以在此仅对采样信号进行9层分解。如图8所示为经过小波分解、重构、频带划分及成分合成等处理后得到的表面轮廓的3种不同尺度形貌误差成分，其中横坐标为采样点序数，纵坐标为不同成分所对应的高度值，单位为μm。

图8　轮廓误差成分多尺度表征

通过仿真分析得到了产品截面轮廓多尺度形貌误差成分后，将各成分再进行合成，可最终得到如图9所示的具有多尺度形貌误差成分的产品的一个截面的二维轮廓的非理想表面模型。

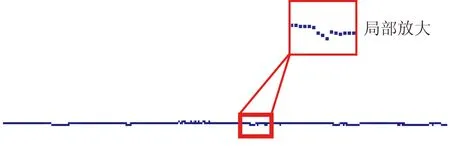
图9　非理想表面模型(二维轮廓)

轮廓是客观评定表面的基础，表面的功能特性在很大程度上取决于表面的多尺度形貌误差[19]，因此可将此研究方法推广至三维离散表面。由于组成图5评定区域的每块取样区域的实测数据为1 024×1 024个采样点的三坐标信息，这会造成进行三维表面形貌误差成分表征时的计算量较大，因此首先对三维采样数据进行数据抽稀，保留128×128个采样点进行后续分析处理。为了使采样数据更为准确，取评定区域中心一块取样区域作为研究对象，利用二维离散小波变换，通过分解、重构、频带划分、成分合成等处理，得到如图10所示的三维表面多尺度形貌误差成分。其中，采样点X及Y坐标表示沿x轴方向及y轴方向对应的采样序数，纵坐标为采样点高度值z，单位为μm。

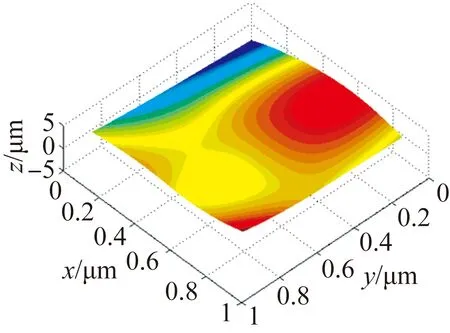
(a)形状误差(a) Form error　(b)波纹度(b) Waveness　(c)粗糙度(c) Roughness

将表面误差各尺度成分进行合成后，得到了如图11所示的能够表征具有宏观及微观多尺度形貌误差成分的三维表面的非理想表面模型。

图11　非理想表面模型(三维表面)

4　结　论

本文以实际工件表面为研究对象，利用白光干涉仪获取了其测量区域内的三维离散点云采样数据。针对对三维表面进行轮廓提取获得的二维离散采样数据，利用离散小波对二维采样数据进行多尺度分解与重构，获得了不同频谱范围内的轮廓形貌误差成分信息。将Talymap软件进行高斯滤波后获得的粗糙度值与利用提出方法所获得的粗糙度值比对，发现平均相对误差值不超过4%，从而证明了研究方法对于二维轮廓形貌误差成分的多尺度表征行之有效。通过将多尺度形貌误差成分进行合成，得到了能够表征工件截面轮廓宏观及微观多尺度形貌误差的非理想表面模型，并成功推广至工件三维表面。

为表征和仿真能够反映加工表面多尺度宏观及微观形貌误差信息的非理想表面模型提供了一种可行可靠的新方法，对于完善GeoSpelling模型、新一代GPS标准体系及推动计算机辅助公差技术的发展均具有重要作用。

[1]蒋向前. 新一代GPS标准理论与应用[M]. 北京：高等教育出版社，2007： 148-150.

JIANG X Q.TheoryandApplicationsofNew-GenerationGeometricalProductSpecifications[M]. Beijing： Higher Education Press， 2007： 148-150.(in Chinese)

[2]郭崇颖，刘检华，唐承统， 等. 基于三维凸包的公差基准轴线拟合[J]. 光学 精密工程， 2014， 22(12)： 3247-3257.

GUO C Y， LIU J H， TANG CH T，etal.. Datum axis fitting for tolerances based on 3D convex hulls [J].Opt.PrecisionEng.， 2014， 22(12)： 3247-3257.(in Chinese)

[3]BALLU A， MATHIEU L， DANTAN J Y. Formal language for GeoSpelling [J].JournalofComputingandInformationScienceinEngineering， 2015， 15(2)： 1-6.

[4]ZHANG M， SHI ZH Y， MATHIEU L，etal.. Geometric product specification of gears： the GeoSpelling perspective [C].Procedingsofthe13thCIRPConferenceonComputerAidedTolerancing，Zhejiang，China， 2015， 27： 90-96.

[5]ISO 17450-1： 2011Geometric product specification(GPS)—General concepts—Part 1： Model for geometrical specification and verification [S].Geneva：InternationalOrganizationforStandardiza-tion， 2011.

[6]ZHANG M， ANWER N， MATHIEU L，etal.. A discrete geometry framework for geometrical product specifications [C].InProcedingsofthe21stCIRPDesignConference，Korea， 2011： 142-148.

[7]张敏，姜海洋，石照耀. 新一代GPS标准中非理想表面模型的建模方法[J]. 仪器仪表学报, 2016, 37(1): 91-98.

ZHANG M, JIANG H Y, SHI ZH Y. Modeling method for the skin model in new-generation geometrical product specifications [J].ChineseJournalofScientificInstrument, 2016, 37(1): 91-98. (in Chinese)

[8]SCHLEICH B， WARTZACK S. Tolerance analysis of rotating Mmchanism based on skin model shapes in discrete Ggometry [C].InProcedingsofthe13thCIRPConferenceonComputerAidedTolerancing，Zhejiang， 2014： 1-6.

[9]李海燕， 刘国栋， 刘炳国， 等. 双密度小波在表面形貌信号分离中的应用[J]. 光学 精密工程， 2008， 16(6)： 1093-1097.

LI H Y， LIU G D， LIU B G，etal.. Application of double density wavelet transform to surface topographic signal separation [J].Opt.PrecisionEng.， 2008， 16(6)： 1093-1097.(in Chinese)

[10]张浩，袁怡宝，张峰. 巴特沃斯小波在表面形貌信号分离中的应用[J]. 光学 精密工程， 2010， 18(7)： 1661-1667.

ZHANG H， YUAN Y B， ZHANG F. Application of Butterworth wavelet to surface topographic signal separation [J].Opt.PrecisionEng.， 2010， 18(7)： 1661-1667.(in Chinese)

[11]任志英，高诚辉，申丁， 等. 双树复小波稳健滤波在工程表面粗糙度评定中的应用[J]. 光学 精密工程， 2014， 22(7)： 1820-1827.

REN ZH Y， GAO CH H， SHEN D，etal.. Application of DT-XWT robust filtering to evaluation of engineering surface roughness [J].Opt.PrecisionEng.， 2014， 22(7)： 1820-1827.(in Chinese)

[12]LU W L， ZHANG G P， LIU X J. Prediction of Surface topography at the end of sliding running-in wear based on areal surface parameters[J].TribologyTransactions， 2014， 57(3)：553-560.

[13]曾文涵. 双树复小波表面分析模型及加工过程形貌辨识方法研究[D]. 武汉：华中科技大学， 2005.

ZENG W H.DualTreeComplexWaveletBasedSurfaceAnalysisModelandTopographyRecognitionforMachiningProcess[D]. Wuhan：Huazhong University of Science&Technology， 2005.(in Chinese)

[14]王明祥， 宁宇蓉， 王晋国. 基于Mallat算法的一维离散小波变换的实现[J].西北大学学报， 2006， 36(3)： 364-368.

WANG M X， NING Y R， WANG J G. Realization of one-dimentional discrete wavelet transform based on Mallat arithmetic [J].JournalofNorthwesternPolytechnicalUniversity，2006， 36(3)： 364-368.(in Chinese)

[15]张志航， 崔海， 丁海娟， 等. MWEDM表面三维粗糙度的小波评定基准面[J]. 哈尔滨工程大学学报， 2011， 32(9)： 1185-1189.

ZHANG ZH H， CUI H， DING H J，etal.. The reference plane by wavelets for 3D roughness evaluation of micro wire electrical discharge machining(MWEDM)[J].JournalofHarbinEngineeringUniversity， 2011， 32(9)： 1185-1189.(in Chinese)

[16]FU SH Y， MURALIKRISHNAN B， RAJA J. Engineering surface analysis with different wavelet bases [J].JournalofManufacturingScienceandEngineering， 2003， 125(4)： 844-852.

[17]GB/T 3505-2009/ISO 4287：1997： 产品几何技术规范(GPS)表面结构 轮廓法 术语、定义及表面结构参数[S]. 北京：中国标准出版社， 2009.GB/T 3505-2009/ISO4287：1997： Geometrical Product Specification(GPS)-Surface texture： Profile method-Terms， definitions and surface texture parameters [S].Standardization Administration of the People’s Republic of China. GB/T 3505-2009. Beijing： Standards Press of China， 2009.(in Chinese)

[18]GB/T 1031-2009：产品几何技术规范(GPS)表面结构 轮廓法 表面粗糙度参数及其数值[S]. 北京：中国标准出版社， 2009.

GB/T 1031-2009: Geometrical Product Specification(GPS)-Surface texture: Profile method-Surface roughness parameters and their values [S]. Beijing: Standards Press of China, 2009.(in Chinese)

[19]张华， 石照耀， 张白. 三维几何形状判别及其误差评定研究[J]. 仪器仪表学报， 2014， 35(6)： 1217-1222.

ZHANG H， SHI ZH Y， ZH B. Study on 3D geometric shape discriminant and form error evaluation [J].ChineseJournalofScientificInstrument， 2014， 35(6)： 1217-1222.(in Chinese)

姜海洋(1989-)，女，吉林吉林人，硕士研究生，2012年于上海师范大学获得学士学位，主要研究方向为产品几何技术规范与认证，精密测量技术，计算机辅助公差设计。E-mail： jiangspeed@126.com

导师简介：

石照耀(1964-)，男，湖南岳阳人，博士，教育部长江学者特聘教授，博士生导师，1984年于合肥工业大学获得学士学位，1988年于陕西机械学院获得硕士学位，2001年于合肥工业大学获得博士学位，主要研究方向为齿轮工程及精密测试技术与仪器。E-mail： shizhaoyao@bjut.edu.cn

(版权所有未经许可不得转载)

Multi-scale representation for skin models in geometrical product specifications

SHI Zhao-yao， JIANG Hai-yang， ZHANG Min

(BeijingEngineeringResearchCenterofPrecisionMeasurementTechnology&Instruments，BeijingUniversityofTechnology，Beijing100124，China)

*Correspondingauthor，E-mail：shizhaoyao@bjut.edu.cn

As most of the Computer Aided Tolerancing tools can only deal with the CAD models with an ideal surface and can not reflect manufacturing errors in physics and geometry, this paper explores a multi-scale representation method for skin model shapes in the Geometrical Product Specification. A discrete data modeling method was proposed for the simulation of topographic errors of surfaces and section profiles of a product in macroscopic and microcosmic scales based on new-generation geometrical product specification. Firstly, a simulation method for multi-scale surface topographic errors based on discrete wavelet was presented. Then, discrete wavelet was used to simulate multi-scale surface topography errors for sampling data of the surfaces and section profiles of a part. Finally, multi-scale surface topography errors were composed and skin models for two-dimentional profile and three-dimentional surface were acquired. The simulation and experiment results show that the proposed method represents skin models with multi-scale surface topographic errors and the average relevant error between the results ofRaobtained by a white-light interferometer and the proposed simulation method is less than 4%. The results verify the correctness and applicability of the proposed method, and provide a valid way for more comprehensive representation of skin model in new-generation geometrical product specification.

geometrical product specification; skin model; discrete geometry; wavelet analysis; multi-scale representation

2016-03-15；

2016-04-20.

国家教育部博士点基金资助项目(No.20131103110001)；国家自然科学基金资助项目(No.51305006)；5北京市教委项目(No.JC001013201402)

1004-924X(2016)07-1647-08

TP391.7；TH701

Adoi:10.3788/OPE.20162407.1647