改进的精密测角法标定面阵摄像机参数

赵振庆，叶　东，张　鑫，陈　刚

(哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 15001)



改进的精密测角法标定面阵摄像机参数

赵振庆，叶东*，张鑫，陈刚

(哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 15001)

改进了用于标定线阵摄像机的传统精密测角算法，标定用于面阵摄像机的参数。该算法利用两束平行光之间的夹角和投影在摄像机上图像点之间的对应关系，在给定一个预测摄像机主点的基础上计算它和实际主点之间的偏差以及摄像机焦距。分析了图像特征提取误差对于平行光夹角测量精度的影响，并给出一种基于平行光夹角误差最小的最优估计，从而进一步提高摄像机内部参数的标定精度。通过仿真实验分析了图像特征提取精度和平行光夹角测量精度对摄像机参数标定精度的影响。结果显示，当图像特征提取精度为0.1 pixel，二维转台精度为0.5″时，主点标定精度可以达到0.56 pixel，焦距标定精度可以达到0.06 mm。利用精度为0.5″的二维转台对摄像机参数进行了实际标定，通过分析像点和标定结果所计算的平行光夹角和实际测量的平行光夹角的误差，可知本文算法的误差是经典精密测角法的68.6%，由此证明该算法对于面阵摄像机参数标定具有更好的结果。

角度测量；面阵摄像机；内部参数；标定精度

1　引　言

在机器视觉研究中，摄像机可以用二维图像信息来表征三维物体信息。为了更好地描述空间物体的三维信息，需要对摄像机的焦距、主点等固有参数进行标定。摄像机模型具有非线性、多参数的特点，为了获得高精度的参数标定结果，大部分参数标定算法都是通过标定摄像机线性模型的初值，然后再优化摄像机的非线性模型来实现的[1-5]。这些标定算法不仅涉及摄像机的内部参数，还涉及到摄像机的外部参数(摄像机坐标系和空间坐标系的关系)，而多个参数的同时标定会影响摄像机内部参数的标定精度。基于平行光的精密测角法利用平行光夹角和摄像机投影点之间的对应关系来标定摄像机参数，由于平行光夹角在刚体变换下具有不变的特性，因而标定模型不涉及摄像机的外部参数。人们对于精密测角法的精度和应用进行了大量研究[6-12]。刘伟毅等[10]提出利用星光代替平行光的方法来简化实验设备，远国勤等[11]利用分组渐进法提高标定精度，RYUSUKE等[12]以平行光夹角恒定为约束来优化标定结果。

传统的精密测角法主要针对线阵摄像机，而对于面阵摄像机来说，它要求平行光旋转的角度方向和摄像机图像的一个坐标轴平行，从而将面阵摄像机分解为两个一维线阵摄像机。该算法需要在标定前调解平行光管上的二维转台和摄像机坐标系之间的旋转关系，由于涉及到两个自由度，因此很难实现。当平行光旋转的角度方向和摄像机图像的一个坐标轴不平行时，平行光夹角和投影图像点之间是较为复杂的非线性关系，同时畸变对于图像点的影响还和图像点的二维坐标值有关，因而传统的精密测角法不再适用。本文基于平行光夹角和投影图像点之间的非线性对应关系提出了一种新的解析算法。该算法在给定预测摄像机主点的基础上，求解出预测值和实际摄像机主点之间的偏差以及摄像机焦距。针对畸变的影响，提出了基于平行光夹角误差最小的优化算法。通过仿真实验验证了图像特征提取精度和平行光夹角测量精度对于标定结果的影响，通过实物实验证明了本文所提出算法的标定精度优于经典的精密测角法。

2　算法原理

2.1投影模型

平行光在摄像机上的投影点可看作过摄像机原点且平行于该平行光的直线和成像平面的交点，如图1所示。两束平行光在图像上的投影点为p1=[u1，v1]，p2=[u2，v2]，根据摄像机透视投影模型，两束平行光的夹角和图像点之间存在如下关系：

(1)

其中Pi=[xi，yi，zi]是图像点pi在摄像机坐标系下的坐标，即：

xi=dx(ui-u0)，yi=dy(vi-v0)，zi=f，i=1，2，

(2)

其中：(u0，v0)是摄像机主点，f是摄像机焦距。这里通过二维精密转台来测量平行光之间的夹角α，通过图像特征提取获得图像点坐标值(ui，vi)，u0，v0，f是待标定的摄像机参数。

图1　平行光夹角和投影点关系

Fig.1Relation of angle between parallel lights with projection image points

由式(1)可知，平行光夹角和图像点之间存在较为复杂的非线性关系，难以直接求解标定参数。这里假设图像点p1和p2关于摄像机主点对称，可以得到：

(3)

带入式(1)可得：

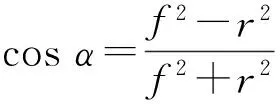
(4)

式(4)说明当平行光投影在以摄像机主点为圆心，以r为半径的圆上另外一对对称点时，平行光之间的夹角是不变的。

实际上由于摄像机主点是未知的，因而假设：

(5)

第一步：求解φ值。

当平行光移动时，由于投影图像点在一个圆内，因此可以得到：

(6)

在已知图像点坐标值(ui，vi)后就可以求解出θ和r。将式(3)、式(5)和式(6)代入式(1)并整理得到：

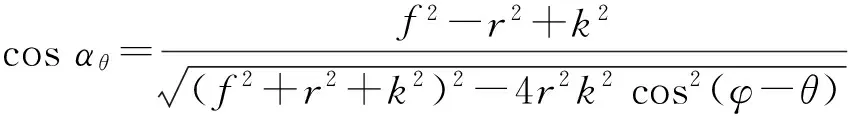
(7)

由式(7)可知，当移动平行光时，即角度θ值发生变化，平行光夹角表达式中分子是个固定值，只有分母发生变化。为了求解φ值，由式(7)可以得到：

(8)

其中cosα0是θ=0时的cosαθ。可以通过式(8)中α值求解h。对于不同的θ值，存在：

(9)

则可以得到：

(10)

第二步：求解k值。

同样根据式(7)可以得到：

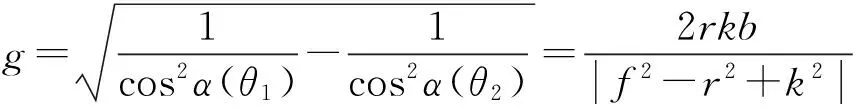
(11)

k2g-2rbk+gf2-r2g=0.

(12)

当θ不同时，改变圆的半径r得到：

(13)

整理式(13)可以得到：

(14)

第三步：求解f值。

最终可以得到摄像机焦距的求解方程，即：

(15)

2.2平行光夹角误差分析

本文算法的前提是平行光投影的图像点位于所定义的圆上，所以实际操作中先在图像平面上定义一个圆，然后在圆上选择一对对称点，调节平行光管上的二维转台，使得平行光投影在这两个图像点上。因此平行光夹角测量精度的影响因素主要有二维转台测量精度和图像特征提取精度。

2.2.1二维转台的测量精度分析

平行光夹角是利用高精度二维精密转台来测量的。根据现有的制造工艺，角度测量精度可以达到小于1″。

2.2.2图像特征的提取精度分析

在式(1)中，根据误差传递理论，图像特征的提取精度对平行光夹角的影响为：

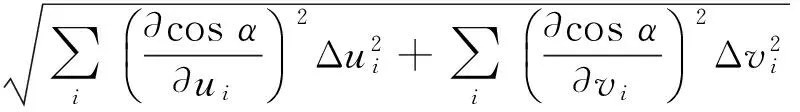
(16)

其中：

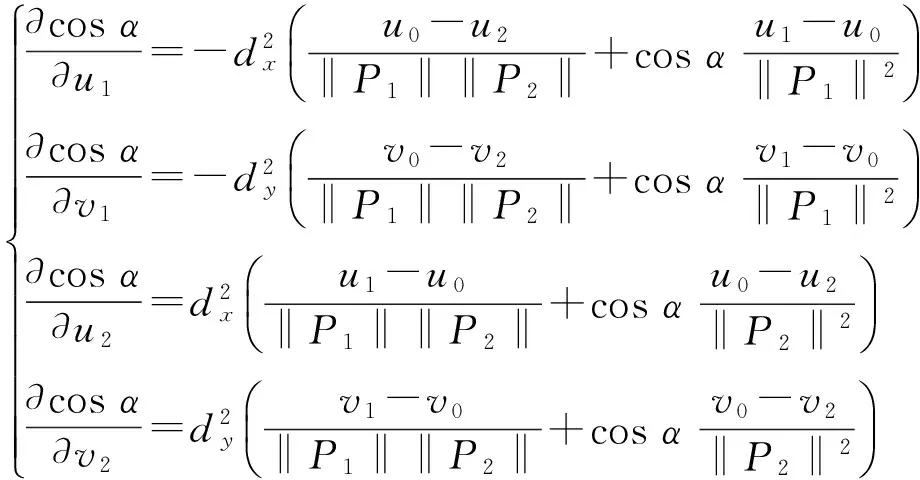
(17)

从式(17)可知，图像点提取精度对平行光夹角的影响和图像点与摄像机主点之间的距离、标定摄像机焦距以及图像点提取精度有关。这里通过matlab仿真来分析这3个因素的影响。

设定摄像机焦距为25 mm，像元尺寸为5.5 μm×5.5 μm，相面大小为1 600 pixel×1 400 pixel，主点像素坐标值为(800， 600)(单位：pixel)，两个图像点分别位于主点的左上角和右下角，距离主点u，v坐标值的距离为10～500 pixel。所有图像点误差都定义为0.1 pixel，仿真结果如图2所示，增大图像点和主点之间的距离会减小图像点误差对平行光夹角的影响，但是由于其值只减小了0.005″，因而其影响可以忽略。

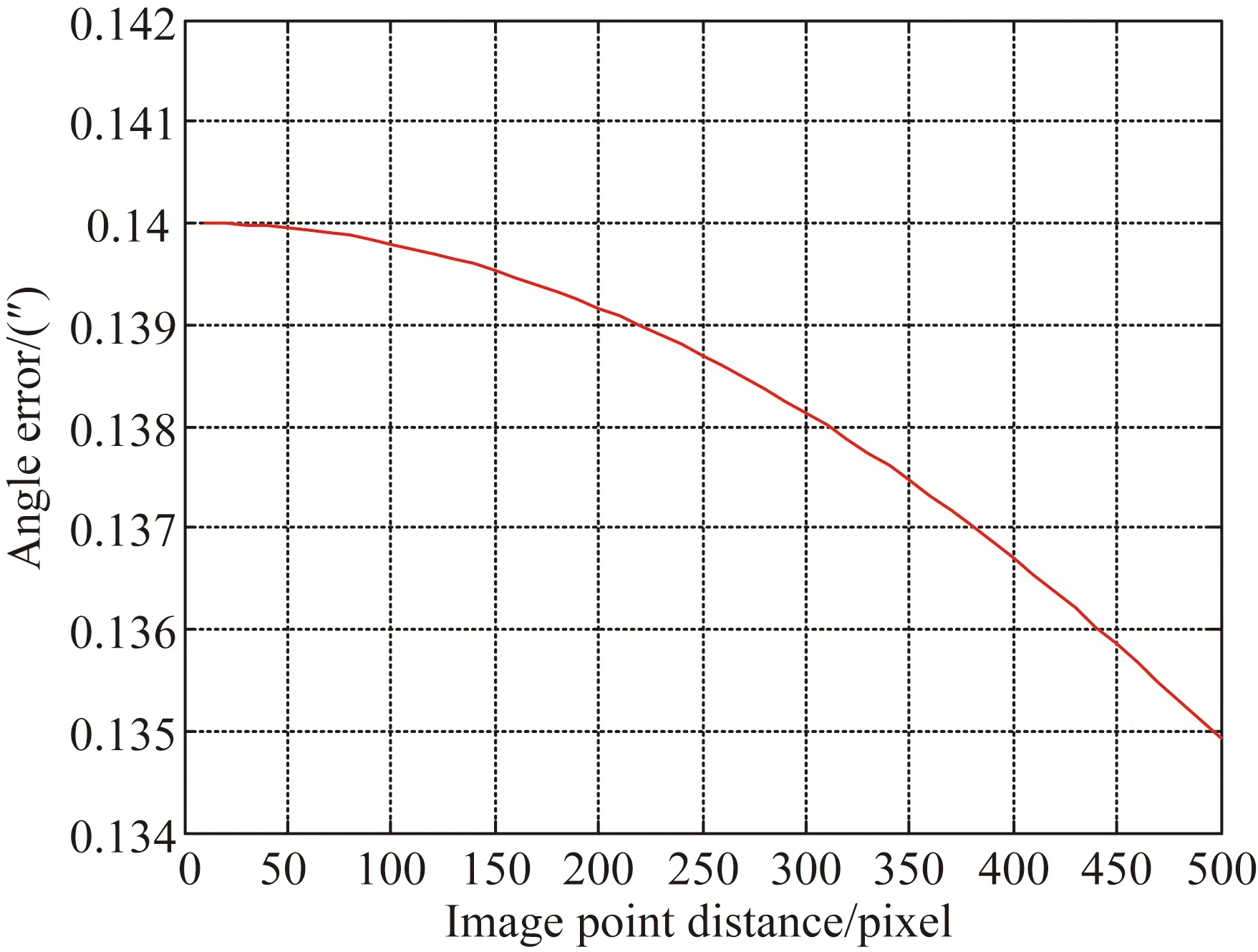
图2　图像点距主点距离的影响分析

Fig.2Impact of distance between image point and optical center point on angle error

为了分析标定焦距的影响，设定摄像机焦距为5～50 mm，两个图像点的像素坐标分别是(400，400)和(1 000，800)(单位：pixel)，所有图像点误差都定义为0.1 pixel，而其他参数不变。仿真结果如图3所示，标定较大焦距的摄像机，图像点误差对平行光夹角的影响较小。当焦距为50 mm 时，0.1 pixel的图像噪声只造成了0.06″的误差。

图3　标定摄像机焦距的影响分析

为了分析图像提取精度的影响，设定图像误差为0.01～0.5 pixel，两个图像点像素坐标分别是(400， 400)和(1 000， 800)(单位：pixel)，摄像机焦距为25 mm，其他参数不变。仿真结果如图4所示，夹角误差随着图像提取误差呈线性增大，当图像点误差为0.1 pixel时，夹角误差为0.11″；当图像点误差为0.5 pixel时，夹角误差为0.53″。在实验室标定时，由于平行光管距离摄像机较近，激光光斑成像比较规则，图像特征提取精度完全可以满足0.1 pixel[13-15]。

图4　图像噪声精度的影响分析

2.3优化算法

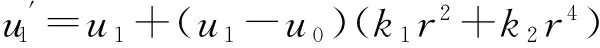
(18)

其中r2=(ui-u0)2+(vi-v0)2。根据已标定出的参数值计算得到平行光夹角为：

(19)

其中α是二维转台的测量角度。因此标定参数值应满足：

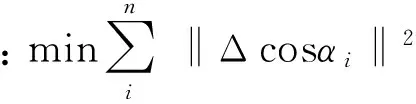
(20)

约束条件为：k，φ，f，k1和k2满足式(10)、式(14)、式(15)和式(18)。

3　实　验

3.1仿真实验

仿真实验中，摄像机焦距为25 mm，像元尺寸为5.5 μm×5.5 μm，相面尺寸为1 600 pixel×1 200 pixel，主点像素坐标是(709.091， 713.636)(单位：pixel)。取相面几何中心(800， 600)(单位：pixel)作为初始主点，则偏差值为(90.909， -113.636)(单位：pixel)。设定平行光通过摄像机主点，这样可以取平行光上一个空间点来描述平行光，该点的投影图像点也就是平行光投影点。通过18对图像点数据线性拟合得到φ，其中θ为0°～170°，每隔10°取一次图像点。通过5组数据线性拟合得到k和f，其中ri值为300～650 pixel，每隔70 pixel取值一次，每个ri值中θ1=φ，θ2=φ+40°，得到不同的bi。优化算法需要5组与主点距离不同的数据，每组数据采集20对图像点。

图5　图像噪声和标定主点精度关系

图6　图像噪声和标定焦距精度关系

仿真主要分析图像噪声和平行光夹角误差对标定精度的影响。图5和图6分析了图像噪声和标定精度的关系，在平行光投影图像点增加均值为0 pixel，标准差为0.05～0.5 pixel的高斯噪声，同时平行光夹角增加均值为0″，标准差为0.5″的高斯噪声。图5为标定主点精度，图6为标定焦距精度。由图可知，主点误差和焦距误差均随着噪声标准差的增大而增大。其中v0误差大于u0误差，这是由于Δv0比Δu0大。当图像噪声标准差小于0.1 pixel，主点误差小于0.56 pixel，焦距误差小于0.06 mm；当图像噪声标准差小于0.35 pixel，主点误差小于1 pixel，焦距误差小于0.1 mm；当图像噪声标准差小于0.5 pixel，主点误差小于1.5 pixel，焦距误差小于0.165 mm，由此可知图像特征提取精度越高标定精度越高。

图7和图8分析了平行光夹角误差和标定参数精度的关系。在平行光夹角增加均值为0″，标准差为0.05～1″的高斯噪声，同时平行光投影图像增加均值为0 pixel，标准差为0.1 pixel的高斯噪声。图7为标定主点精度，图8为标定焦距精度。v0误差仍大于u0误差，当夹角标准差小于0.85″时，主点误差小于1 pixel，焦距误差小于0.1 mm；当夹角标准差小于0.45″时，主点误差小于0.5 pixel，焦距误差小于0.52 mm。

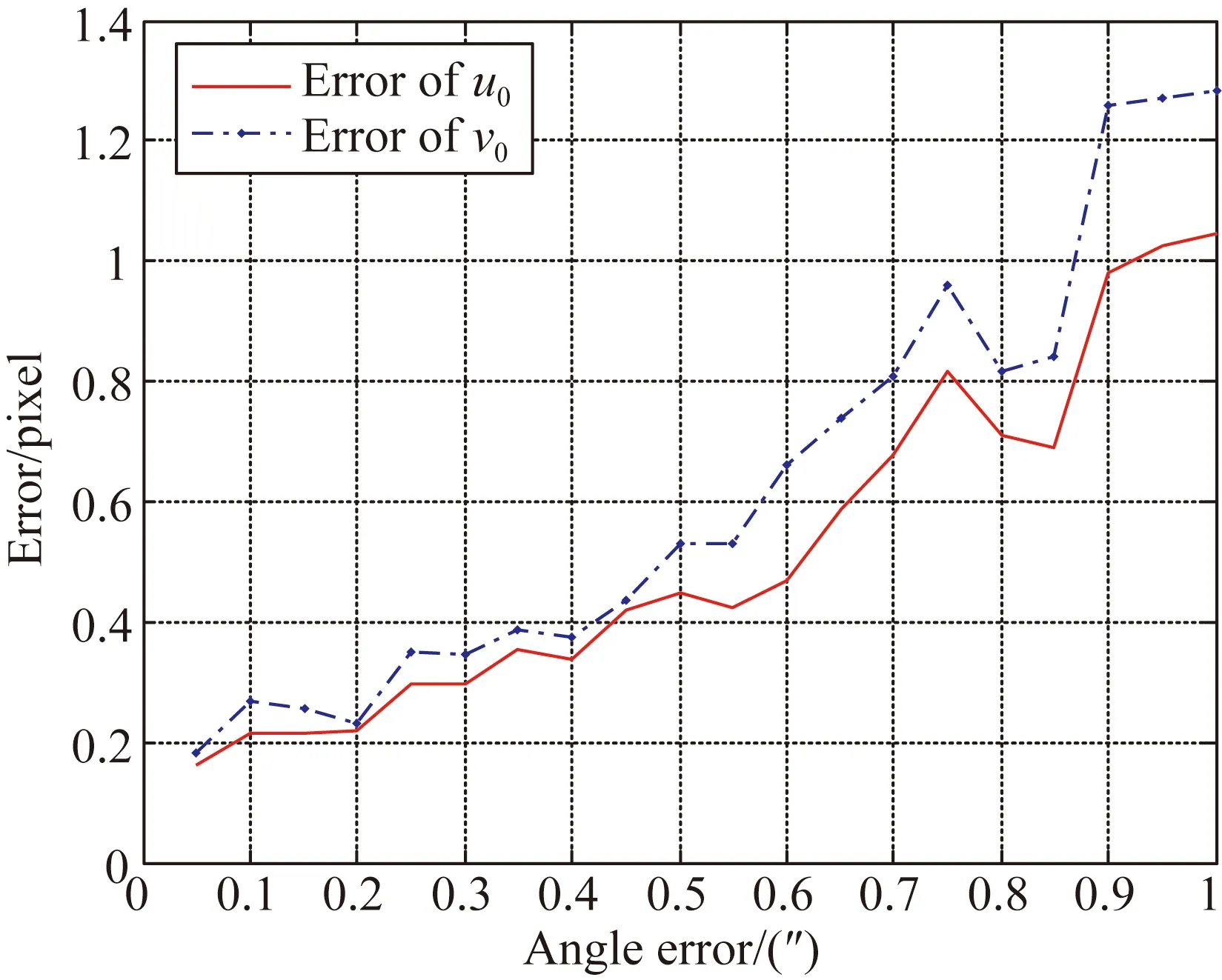
图7　平行光夹角误差和标定主点精度关系

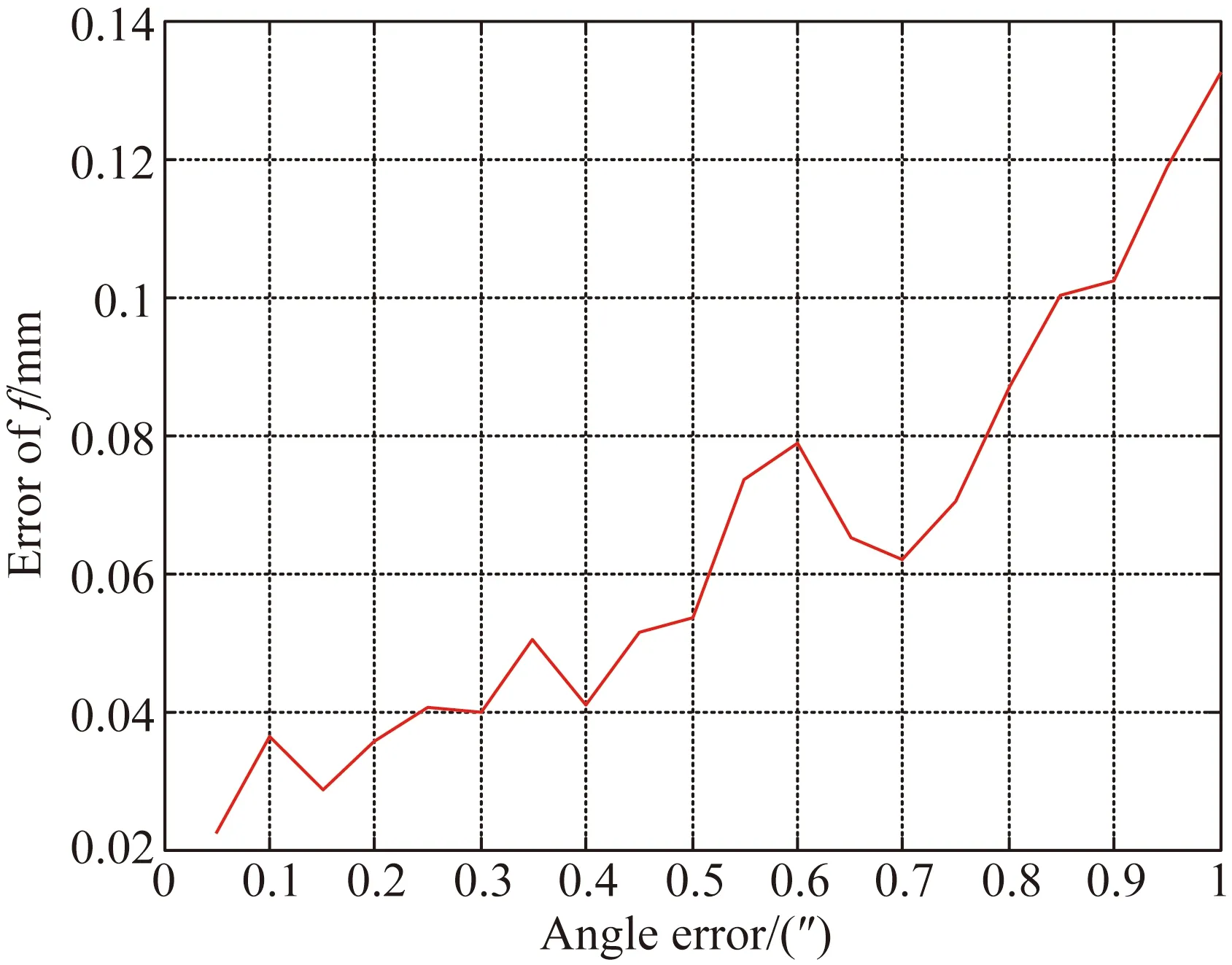
图8　平行光夹角误差和标定焦距精度关系

3.2实物实验

实验现场如图9所示，摄像机采用Kowa公司的LM25JCM镜头，焦距为25 mm。摄像机选取的是AVT公司的GT1660，相面尺寸为1 600 pixel×1 200 pixel。平行光管固定在高精度二维转台上，转台精度是0.5″。摄像机距离转台约为1 m，转台和摄像机数据通过控制电脑来处理。

图9　实物实验

将本文所提出的算法和经典的精密测角法做对比。在经典的精密测角法中，调整二维精密转台和摄像机坐标系之间的关系，使得在图像平面u方向的投影图像点的v坐标值最大偏移量为0.5 pixel，同样在v方向图像点的u坐标值的最大偏移量为0.5 pixel。每个方向采集100个图像点，本文算法和经典测角法的计算结果如表1所示。由表1可知，标定焦距值相差很小，但是主点坐标值相差最大有1.88 pixel，这是由于不能完全保证二维转台坐标轴和摄像机坐标系平行所带来的误差。为了对比两种算法的标定精度，利用标定结果和图像点根据式(1)来计算平行光夹角，并将其和二维转台测量结果做比较。以主点附近为圆心，选择10个不同半径的圆，每个圆上选择10个图像点，总共有101个数据点。比较结果如图10所示，两种算法的标定结果所计算的夹角误差随着圆半径及平行光夹角的增大而变大，而基于本文所提出算法的误差更小。基于经典测角算法的最大误差是-73.52″，基于本文所提出算法的最大误差是-50.4″，误差减小了23.12″。

表1　摄像机参数标定结果

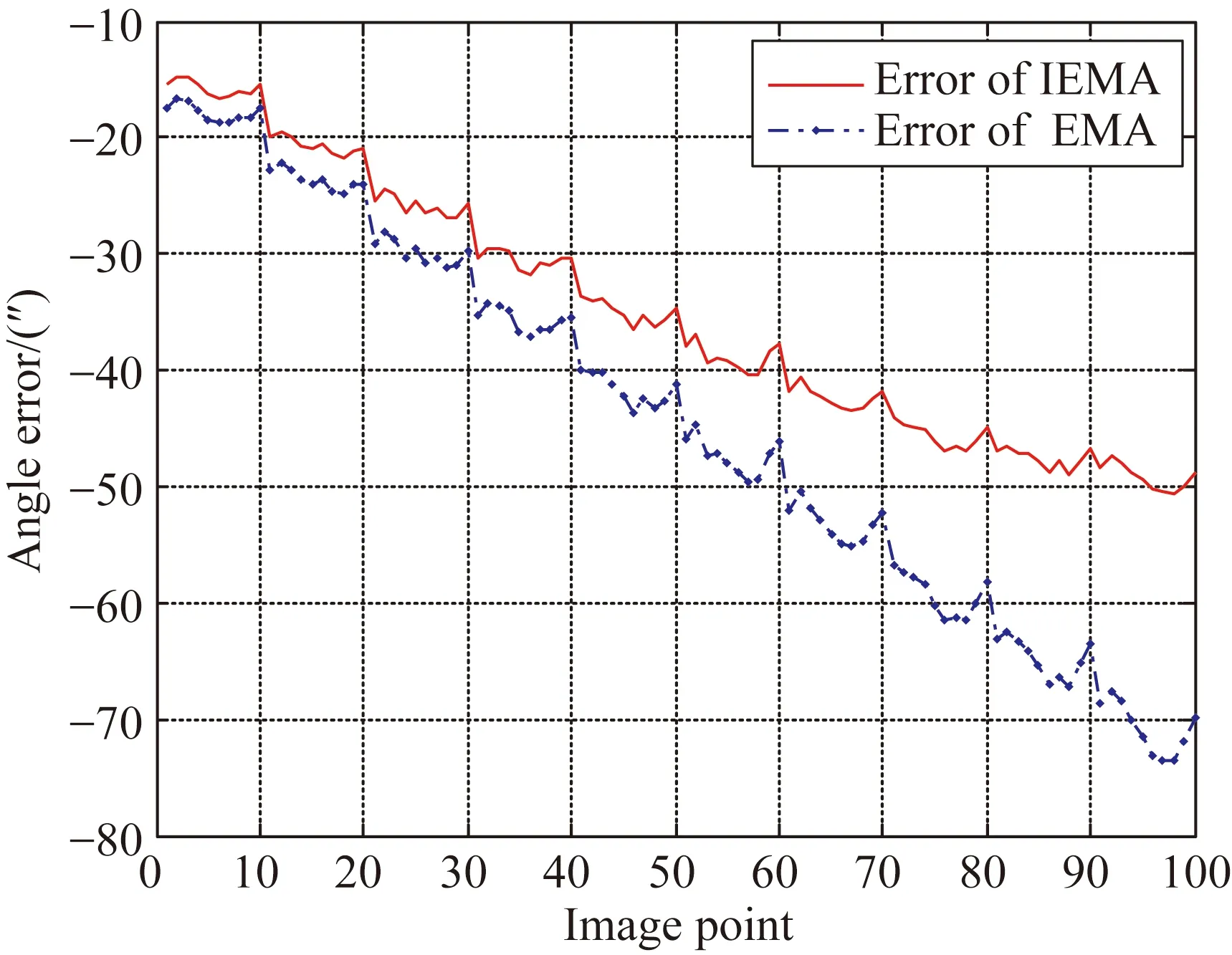
图10图像点计算的平行光夹角误差

Fig.10Parallel light angle errors calculated by image points

5　结　论

传统的精密测角法在标定面阵摄像机时要求二维转台坐标系和摄像机坐标系平行，本文提出了一种改进的精密测角法，可在两个坐标系的任意姿态下标定出摄像机的内部参数。该算法在给定一个预测摄像机主点坐标值下计算出它和实际主点坐标值之间的偏差，同时计算出摄像机的焦距。由于该算法设定平行光投影在图像平面的圆上，因此本文还分析了图像特征提取精度对平行光夹角误差的影响。仿真实验表明，该算法在图像特征提取精度为0.1 pixel，二维转台精度为0.5″时，主点标定精度小于0.56 pixel，焦距标定精度小于0.06 mm。实验对比本文算法和经典精密测角法可知，该算法所计算的平行光夹角误差为经典精密测角法误差的68.6%，从而证明该算法具有更好的标定结果。

[1]刘书桂，姜珍珠，董英华，等.采用移动光靶标的分区域相机标定[J].光学 精密工程，2014，22(2)： 259-265.

LIU SH G， JIANG ZH ZH， DONG Y H，etal.. Sub-regional camera calibration based on moving light target [J].Opt.PrecisionEng.， 2014， 22(2)： 259-265.(in Chinese)

[2]叶峰，王敏，陈剑东，等.共面点的摄像机非线性畸变校正[J].光学 精密工程，2015，23(10)： 2962-2970.

YE F， WANG M， CHEN J D，etal.. Camera nonlinear distortion correction based on coplanar points[J].Opt.PrecisionEng.， 2015， 23(10)： 1962-1970.(in Chinese)

[3]朱伟东，曹良洪，梅标，等. 利用圆心不对称投影精确标定工业相机[J].光学 精密工程，2014，22(8)： 2267-2273.

ZHU W D， CAO L H， MEI B，etal.. Calibration of industrial cameras using asymmetric circle center projection[J].Opt.PrecisionEng.， 2014， 22(8)： 2267-2273.(in Chinese)

[4]黄风山，钱惠芬. 三坐标测量机驱动的摄像机标定技术[J].光学 精密工程，2010，18(4)： 952-957.

HUANG F SH， QIAN H F. Camera calibration technology driven by three-coordinate measuring machine[J].Opt.PrecisionEng.， 2010， 18(4)： 952-957.(in Chinese)

[5]王子辰，戴明，李刚，等. 基于虚拟立体靶标的线性相机标定与分析[J].红外与激光工程，2014，43(3)： 902-907.

WANG Z CH， DAI M， LI G，etal.. Calibration and analysis of line-scan camera based on virtual stereo pattern[J].InfraredandLaserEngineering， 2014， 43(3)： 902-907.(in Chinese)

[6]吴国栋，韩冰，何喣，等. 精密测角法的线阵CCD相机几何参数实验室标定方法[J].光学 精密工程，2007，15(10)： 1628-1632.

WU G D， HAN B， HE X. Calibration of geometric parameters of line-array CCD camera based on exact measuring angle in lab[J].Opt.PrecisionEng.， 2007， 15(10)： 1628-1632.(in Chinese)

[7]刘伟毅，贾继强，丁亚林，等. 精密测角法中测量误差对内方位元素标定的影响[J].红外与激光工程，2009，38(4)： 705-709.

LIU W Y， JIA J Q， DING Y L，etal.. Measurement error impact on intrinsic parameters calibration in precise angle measurement method[J].InfraredandLaserEngineering， 2009， 38(4)： 705-709.(in Chinese)

[8]LIU W Y， DING Y L， JIA J Q. Factor analysis for impactions on principal point accuracy in exact measuring angle method[C].InternationalSymposiumonPhotonicsandOptoelectronics，Chengdu，China， 2010.

[9]刘波，贾继强，丁亚林. 基于测角法的CCD航测相机实验室几何标定[J].激光与红外， 2010，40(3)： 298-301.

LIU B， JIA J Q， DING Y L. Geometric calibration with angle measure for CCD aerial photogram metric camera in laboratory [J].Laser&Infrared， 2010， 40(3)： 298-301.(in Chinese)

[10]刘伟毅，丁亚林， 贾继强，等. 借助于星点标定相机的内方位元素[J].光学 精密工程，2010，18(9)： 2086-2093.

LIU W Y， DING Y L， JIA J Q，etal.. Calibration of inner orientation elements for camera by means of star points[J].Opt.PrecisionEng.， 2010， 18(9)： 2086-2093.(in Chinese)

[11]远国勤，丁亚林， 惠守文，等. 基于精密测角法的测绘相机分组渐进标定算法[J].光学学报，2012，32(1)： 0112005.

YUAN G Q， DING Y L， HUI SH W，etal.. Grouped approach algorithm for mapping camera calibration based on method of exact measuring angle[J].ActaOpticaSinica， 2012， 32(1)： 0112005.(in Chinese)

[12]RYUSUKE S， YASUSHI Y. Accurate calibration of intrinsic camera parameters by observing parallel light pairs[C].InternationalConferenceonRoboticsandAutomation，Pasadena，CA，USA， 2008：1390-1397.

[13]姚志军，韩秋蕾. 激光制导动靶照射精度测量系统[J].液晶与显示，2014，29(6)： 1124-1130.YAO ZH J， HAN Q L. Laser radiation accuracy measurement system of moving target in laser guidance[J].ChineseJournalofLiquidCrystalsandDisplays， 2014， 29(6)： 1124-1130.(in Chinese)

[14]赵婧鑫，周富强. 小尺寸光斑中心的高精度定位算法[J].红外与激光工程，2014，43(8)： 2690-2693.

ZHAO J X， ZHOU F Q. High precision center location algorithm of small scale focal spot[J].InfraredandLaserEngineering， 2014， 43(8)： 2690-2693.(in Chinese)

[15]王林波，王延杰，邸男，等. 基于几何特征的圆形标志点亚像素中心定位[J].液晶与显示，2014，29(6)： 1003-1009.WANG L B， WANG Y J， DI N，etal.. Subpixel location of circle target center based on geometric features[J].ChineseJournalofLiquidCrystalsandDisplays， 2014， 29(6)： 1003-1009.(in Chinese)

赵振庆(1983-)，男，河北张家口人，2007年、2010年于燕山大学分别获得学士、硕士学位，主要研究方向为机器视觉、图像处理。E-mail：zzq725@126.com

导师简介：

叶东(1968-)，男，湖北武汉人，博士，教授，博士生导师，1990年、1995年和1999年于哈尔滨工业大学分别获学士、硕士和博士学位，主要从事基于串/并联结构的坐标测量理论和技术、双目/单目视觉坐标测量理论和技术等方向的研究。E-mail：yedong@hit.edu.cn

(版权所有未经许可不得转载)

Calibration of area-array camera parameters based on improved exact measuring angle method

ZHAO Zhen-qing， YE Dong*， ZHANG Xin， CHEN Gang

(SchoolofElectricalEngineeringandAutomation，HarbinInstituteofTechnology，Harbin150001，China)

*Correspondingauthor，E-mail：yedong@hit.edu.cn

An improved exact measuring angle algorithm is proposed for parameter calibration of area array cameras. Based on a given estimated principal point of camera, the algorithm calculated deviation between the estimated and actual principal points and focal distance of the camera by using the corresponding relationship between intersection angle of two beams of parallel lights and image point of projection on the camera. The influence of image feature extraction error on intersection angle measurement accuracy of parallel lights was analyzed and an optimal estimation based on the minimum intersection angle error of parallel lights was employed so as to promote the calibration accuracy of internal parameter of the camera. Simulation experiment was conducted to analyze the influence of image feature extraction accuracy and intersection angle measurement accuracy of parallel lights on camera parameter calibration precision. The results show that the calibration accuracies of principal point and focal distance can reach 0.56 pixel and 0.06 mm respectively when image characteristics extraction accuracy is 0.1 pixel and two-dimensional rotary table accuracy is 0.5″. An two-dimensional rotary table with accuracy reaching 0.5″ is used for parameter calibration of the camera. In comparison of intersection angle error of parallel light calculated based on image point and calibration results with the calibration result, the error of the improved algorithm is 68.6% of the classic exact measuring angle method. This proves that the proposed algorithm has a better accuracy in parameter calibration of area array camera.

angle measurement; area-array camera; intrinsic parameters; calibration precision

2016-01-08；

2016-03-17.

国家自然科学基金资助项目(No.51075095)；黑龙江省自然科学基金资助项目(No.E201045)

1004-924X(2016)07-1592-08

TP391.4；TB92

Adoi:10.3788/OPE.20162407.1592