剪切流场中聚乙烯结晶过程的建模与模拟

阮春蕾，刘春太

（1河南科技大学数学与统计学院，河南 洛阳 471023；2橡塑模具国家工程研究中心，河南 郑州 450001）



剪切流场中聚乙烯结晶过程的建模与模拟

阮春蕾1，2，刘春太2

（1河南科技大学数学与统计学院，河南 洛阳 471023；2橡塑模具国家工程研究中心，河南 郑州 450001）

基于Eder模型推导了剪切流场中球晶、串晶形态演化的数学模型，将第一法向应力差作为串晶成核的驱动，并引入两相悬浮模型描述体系，认为其由无定形相和半结晶相组成，分别用FENE-P模型和刚性哑铃模型描述。基于上述数学模型，分别构造了捕捉球晶、串晶生长的Monte Carlo法与体系控制方程求解的有限差分法，成功模拟了二维剪切流场中聚乙烯的结晶过程，给出了球晶、串晶的形态演化，分析了剪切时间、剪切速率对串晶成核密度、结晶速率、流体黏度等的影响。数值结果表明：所构造的Monte Carlo法合理有效，不仅成功捕捉了晶体的生长与碰撞，而且较为准确地预测了结晶速率。此外，提高剪切时间或剪切速率，将增加串晶成核密度、提高结晶速率、使流体黏度突增的时间点提前。

流动诱导结晶；形态学；动力学；Monte Carlo模拟；结晶

DOI：10.11949/j.issn.0438-1157.20151472

引　言

聚合物的结晶过程及其形态演化是决定制品力学性能的关键因素［1］。广义而言，聚合物必须经过成型加工才能成为有用的制品。成型过程中，聚合物受到流场的作用，高分子链发生运动，在低温条件下形成凝聚态结构，并最终形成球晶、串晶等复杂结晶形态［1］。由于成型中以剪切流场居多，因此，本文将研究限定在简单剪切流场下，并以聚乙烯为代表，研究结晶形态与动力学，流体性质等的改变，揭示外场因素与结晶过程间的相关规律，并为复杂成型条件下的结晶过程提供指导。

流场中的聚合物结晶又被称为流动诱导结晶（flow induced crystallization，FIC）［1-2］。流动诱导结晶的实验研究表明［1］：与静态结晶相比，流场中的结晶发生了实质性变化，不仅提高了结晶速率，而且改变了结晶形态（不同于静态条件下的球晶，流场作用下可获得高度异相的串晶结构）。基于上述实验结果，许多学者提出了不少关于流动诱导结晶的动力学模型，其建立大多基于Nakamura方程［3］和Kolmogorov方程［4］。如，Doufas等［5］、Tanner等［6-7］通过修正Nakamura方程得到了流动诱导结晶动力学模型；Koscher等［8］、Zheng等［9］认为流动提高了晶体的成核数，并将其反映在Kolmogorov方程中，得到了流动诱导结晶动力学模型。该类方法的主要缺点在于不能提供较为详细的微观结构信息。Eder等［10］首次提出了基于结晶形态的数学模型。他们把球晶看成是不断长大的球，串晶看成是不断长大的圆柱体，得到一系列微分方程组。Zuidema等［11］对其进行了改进，用可恢复形变替代Eder模型中流场应变率作为串晶成核的驱动。他们的模型较为成功地反映了串晶的微观信息，但相关研究并没有显式地采用模拟方法给出其成核、生长与碰撞的演化细节。因此，仍然摆脱不了使用结晶动力学模型。Guo等［12］引入了大分子链形变因子，他们认为当形变因子大于某临界值时，结晶按串晶形式生长；反之，按球晶形式生长。他们利用该方法成功预测了iPP注塑制件的皮层厚度，但未得到结晶形态细节。

国内关于流动诱导结晶数值模拟方面的研究也不多见。王锦燕等［13］、荣彦等［14］对剪切流场中的聚合物结晶进行了模拟，定性分析了剪切对结晶过程及流体性质等的影响。他们的研究并未涉及到结晶形态。Zhou等［15］采用Guo等［12］的方法对成型中的结晶形态进行了显示，区分了球晶和串晶，但相关研究并没有将其与结晶动力学建立联系，而只是给出了结晶形态的可能表示。

本文基于Eder模型推导了剪切流场中球晶、串晶的形态演化模型，并采用Monte Carlo法［16］成功模拟了二维剪切流场中聚乙烯的结晶过程，给出了球晶、串晶的形态演化，分析了剪切时间、剪切速率对串晶成核密度、结晶速率、流体黏度、体系应力的影响。

1　模型与算法

1.1结晶动力学模型

Avrami方程［17］是聚合物结晶动力学模型中应用最广的模型，它也可用于描述流场中的聚合物结晶，其具体表达式为

其中，0φ为球晶的“虚幻体积”，0ψ为串晶的“虚幻体积”。Eder等［10］给出了0φ和0ψ的表达式，其中，描述三维球晶生长的方程组为

这里，Ns、Rtot、Stot、Vtot分别为球晶的晶核数、总体直径长度、总体表面积、总体体积；而a为成核速率相关的参数，Gs为球晶的生长速率。三维串晶生长的方程组为

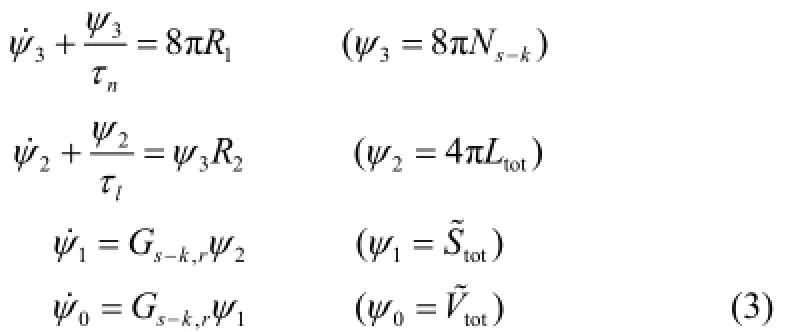
这里，Ns-k、Ltot、S~tot、V~tot分别为串晶的晶核数、总体长度、总体表面积、总体体积；而τn为与温度相关的串晶成核率参数，为串晶成核的驱动参数，γ.为应变率，为拟合参数；τl为与温度相关的串晶轴向生长率参数，为串晶轴向生长率的驱动参数，为拟合参数，Gs-k，r为串晶径向生长速率。

Eder模型中将球晶视为不断长大的球，而串晶视为不断长大的圆柱体。本文研究二维情况下的晶体生长，此时，认为球晶按圆形生长，而串晶按长方形生长。

由式（2）可导出三维球晶的等价微分方程组，将其降为二维，则有

从中可知，球晶的生长由成核数sN及生长速率sG所决定。采用如下的成核密度公式［2］

其中，sN是过冷度TΔ的函数，过冷度TΔ定义为为平衡熔点，0N和ϕ是经验参数。球晶的生长速率用Hoffman-Lauritzen方程表示［18］

其中，G0、Kg为参考因子，U∗为聚合物的分子活化能，Rg为气体常数，T∞=Tg-30，Tg为玻璃化转变温度，

由式（3）可导出三维串晶的等价微分方程组，同样，将其降为二维，有

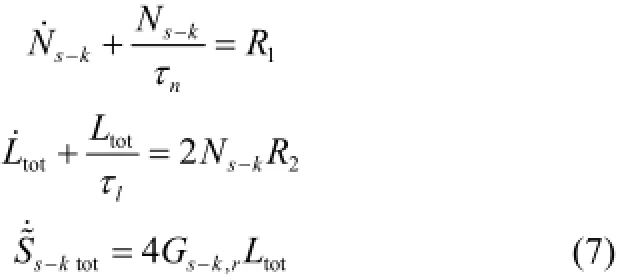
这里，认为参数nτ=∞，lτ=∞［11］，则有

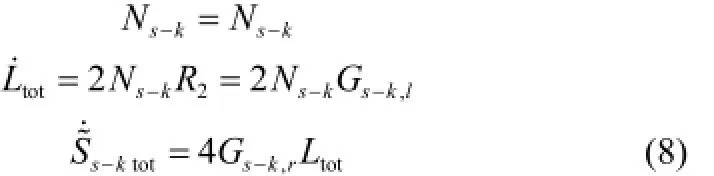
由式（8）可知，串晶的生长由串晶成核密度Ns-k、串晶轴向生长速率Gs-k，l以及串晶径向生长速率Gs-k，r决定。串晶轴向生长速率Gs-k，l，可记为［10］

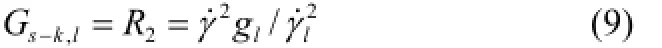
一般情况下，认为串晶径向生长速率Gs-k，r与球晶生长速率Gs一致［11］，即

问题的关键在于求解串晶成核密度。采用如下公式［8］

其中，C为参数，N1为体系的第一法向应力差。

1.2无定形相与半结晶相的模型

式（11）中出现了第一法向应力差，因此，必须对晶体所在体系做一下阐述。这里，采用Zheng等［9］的思想，认为半结晶相悬浮于无定形相之中，无定形相采用FENE-P弹性哑铃模型描述，而半结晶相采用棒状哑铃模型来描述。

无定形相的FENE-P弹性哑铃模型为［19］

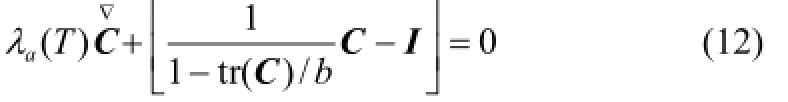
其中，C为大分子链构型张量，λa（T）为分子松弛

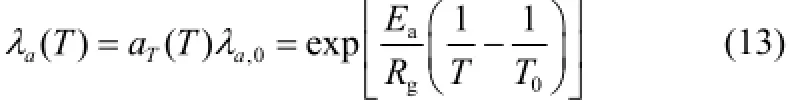
其中，，0aλ为温度为0T时的分子松弛时间，ag/ER为拟合常数。

无定形相对应力的贡献为［9，19］

其中，aτ为无定形相应力，n为分子密度，k为Botzmann常数。

半结晶相中的分子不能拉伸，只能取向，故采用硬棒模型来描述［9］，其动力学方程为

其中，为分子构型张量，γ.为形变率张量，λsc（x，T）为棒状哑铃的松弛时间，采用如下公式［9］α为相对结晶度，A为经验值。式（15）中的四阶张量<>RRRR，采用如下的二次封闭近似［9］半结晶相对体系应力的贡献为［9］

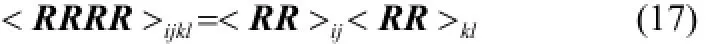
这里，ηsc（x，T）为半结晶相的黏度，与无定形相的黏度间满足如下关系［9］

至此，整个体系就完整描述出来。由式（14）、式（18）可得到体系的整体应力表达式而式（11）中的第一法向应力差N1=τ11-τ22由式（20）计算得到。

1.3算法分析

1.3.1Monte Carlo法本文采用Monte Carlo法［16］来捕捉结晶形态的演化。这里，研究对象设为空间中某块特定区域上［0，1］mm×［0，1］mm的聚合物。给定温度、剪切速率及剪切时间，并按式（5）、式（6）计算球晶成核密度Ns、球晶生长速率Gs；按式（9）～式（11）计算串晶轴向生长速率Gs-k，l、串晶径向生长速率Gs-k，r以及随时间变化的串晶成核密度Ns-k。

实施时，先将区域剖分为Ntot个小单元，这里取Ntot=106，并对每个单元赋底色。在t=0时生成密度为Ns的球晶晶核和密度为Ns-k的串晶晶核，并对晶核赋颜色。在t时刻，计算球晶的半径R=Gst，对于每一个球晶，生成足够多的随机点，若该点的颜色为底色，则判断其坐标是否落入该球晶范围内，若是则认为该点被此球晶覆盖，赋上该球晶的颜色；对于串晶，由于其成核与时间相关，先由式（11）计算串晶的成核密度，随机产生新生核的坐标并赋值，同时，计算串晶的长度l=2Gs-k，l及半径R=Gs-k，r，对于每一个串晶，生成足够多的随机点，判断其是否落入某串晶长度及半径覆盖的长方形中，若是则赋上该串晶的颜色。如此循环，直到所有单元都被晶体覆盖，则结束。需要指出的是，上述t~的计算与串晶的晶核生成时间相关，从晶核生成后开始计时。此外，相对结晶度的计算，这里采用式（21）来表示。

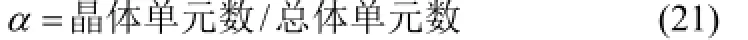
其中，晶体单元数可根据单元颜色来统计，而总体单元数为totN。Monte Carlo法的优势在于可以避开使用结晶动力学模型。常见的结晶动力学模型，如Avrami方程和Kolmogorov方程，在处理球晶、串晶共混体系时遇到困难，很难确定形状因子mC和n。而Monte Carlo法直接从形态演化中统计获得可信的相对结晶度，避免了由结晶动力学模型中参数的不确定而导致的误差。

1.3.2有限差分法无定形相与半结晶相方程的计算采用有限差分法。演化方程式（12）和式（15）采用时间一阶向前进行离散，即

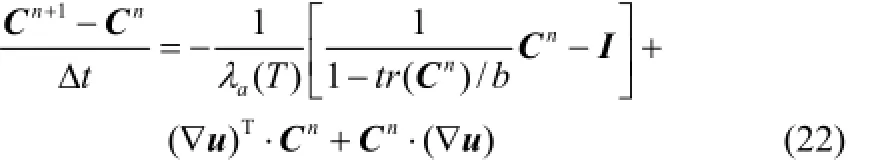
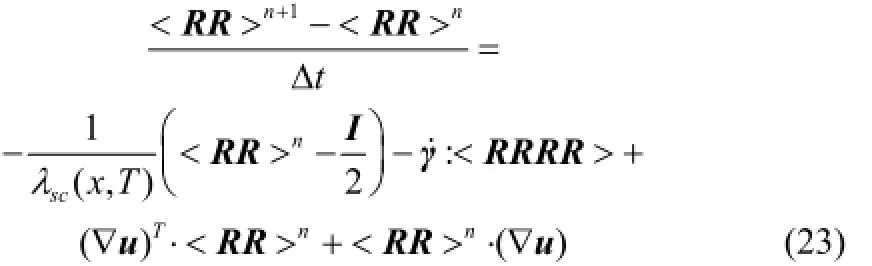
2　结果与讨论

2.1材料参数

本文以聚乙烯为代表，考察结晶过程及流体性质。模拟所用参数为：N0=17.4×106，ϕ=0.155， G0=2.83×102m/s，，Kg=5.5×105K2，Tg=269 K，=2.69×10-7， C=105Pa-1·s-1·m-1，λa，0=4.00×10-2s，T0=476.15 K，Ea/Rg=5.602×103K，b=5，n= 1.26×1026/m3，k=1.38×10-23，β=9.2，β1=0.05，A=0.44。其中，结晶形态参数见文献［8，11］，无定形相及半结晶相参数见文献［9］。

2.2算法有效性验证

为了验证算法的有效性，将模拟结果与Eder模型预测结果进行比较。这里，假定球晶和串晶晶核瞬时产生，且有成核密度Ns=107m-2，Ns-k=107m-2，球晶按生长速率Gs=10-6m·s-1进行生长，串晶按径向生长速率Gs=10-6m·s-1及轴向生长速率Gs-k，l=10-5m·s-1进行生长。图1给出了模拟结果与理论模型预测所得相对结晶度的比较。由图可知，模拟结果与理论预测值吻合得较好。模拟结果主要在结晶后期发生偏离，这可能是由于Eder模型的建立是基于Avrami方程的，而该方程在建模时并未考虑到晶体间的碰撞。这也是Avrami方程的主要局限性。

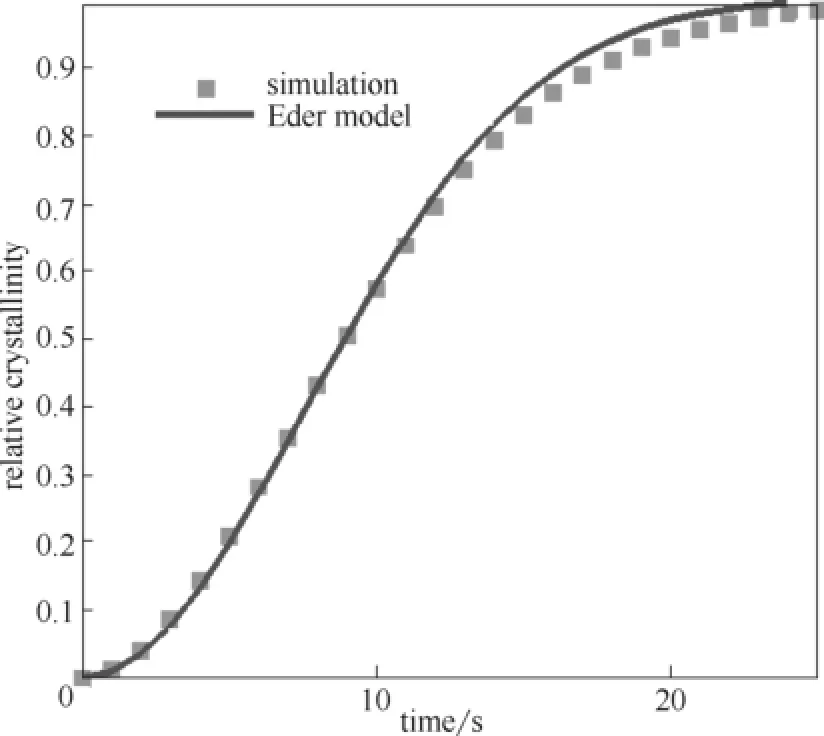
图1　数值解与Eder模型的比较Fig.1　Comparison of simulation result with Eder model

2.3剪切时间的影响本节讨论剪切时间的影响。为了便于分析，这里固定剪切速率γ.=10 s-1，温度T=137℃。

2.3.1结晶速率及形态的变化图2为剪切时间t=0、1、5、10 s时所生成的串晶成核密度。其中，t=0代表不对流体进行剪切，即静态条件。施加剪切后，串晶的成核密度将有所增加；且剪切时间越大，串晶成核密度越大。当剪切停止后，成核密度将不再随时间的变化而变化。

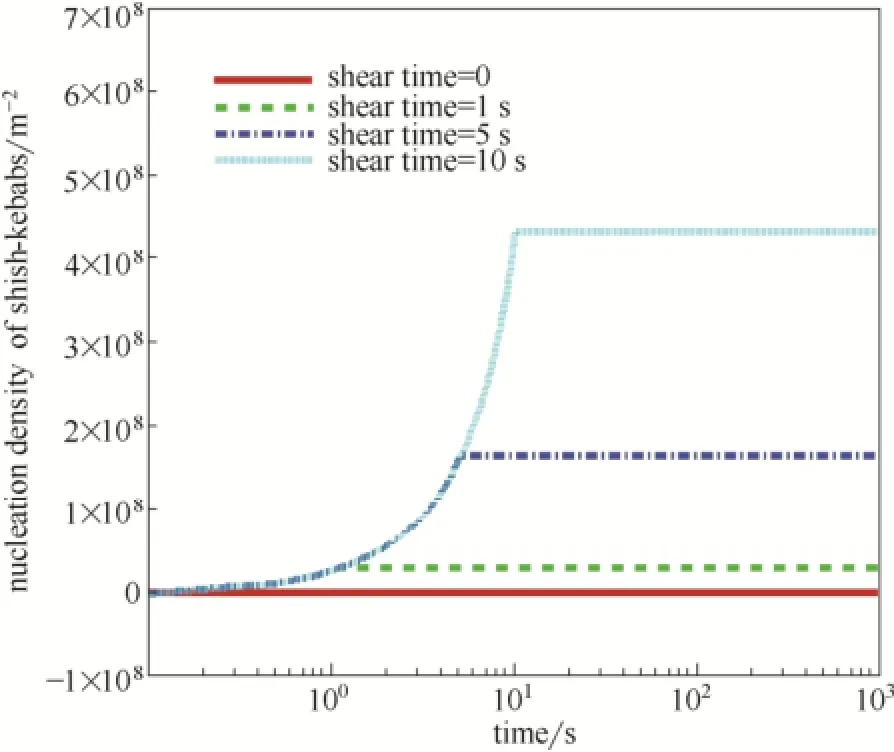
图2　不同剪切时间下的串晶成核密度Fig.2　Nucleation density of shish-kebabs with different shear time

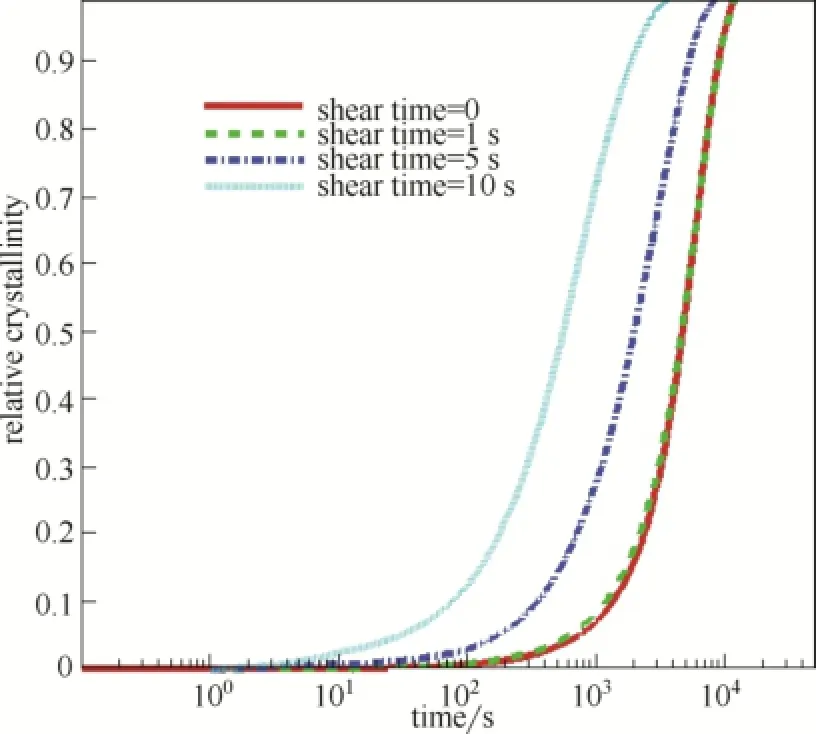
图3　不同剪切时间下的相对结晶度比较Fig.3　Relative crystallinity comparison with different shear time

图3为不同剪切时间下的相对结晶度演化。与静态条件（t=0）相比，剪切时间越大，结晶速率越快。结晶的加速作用主要是由剪切诱导的串晶所贡献的。由于流场的剪切作用，促使串晶晶核的产生，并提供轴向的生长速率，使串晶成长，进而加速结晶过程。在剪切时间较小的情况下，所提供的串晶晶核相对较少，其加速作用不甚明显。文献［9］也报道了大剪切时间对结晶速率的加速作用。一些学者［13-14］认为这种加速不是无限制的，当剪切时间达到某临界值时，加速作用会变得缓慢。

图4给出了剪切时间为0、5、10 s时的结晶形态比较。由图可知，随着剪切时间的增加，结晶形态发生较大变化：不仅提高了串晶成核密度，而且提高了串晶的各向异性。这种变化趋势与Zhou等［15］的实验结果也是一致的。

2.3.2流体黏度及应力的变化图5给出了剪切时间t=0、1、5、10 s时流体黏度的变化。黏度随着时间的增加在某临界值时会发生突增现象。这是由相对结晶度引起的。由式（19）知，ηsc（x，T）=，当α接近常数A时，ηsc将趋向于无穷；故体系黏度急剧变化。此外，剪切时间越大，流体黏度越早发生突增。这与Zheng等［9］的结果一致。

图6为剪切时间t=10 s时的剪切应力和第一法向应力差。应力值在前期变化较为缓慢，而到临界值附近变化剧烈，该临界值对应于相对结晶度。当结晶完成时，这些应力将锁在材料内部，形成残余应力［20］。

2.4剪切速率的影响

本节讨论剪切速率的影响。为了便于分析，这里固定剪切时间t=10 s，温度T=137℃。

2.4.1结晶速率及形态的变化图7给出了剪切速率0γ=.、1、5、10 s-1时串晶成核密度的比较。其中，γ=.0代表不对流体进行剪切，即静态条件。由图可知，剪切速率越大，串晶成核密度越大。当剪切停止后，成核密度将不再随时间的变化而变化。

图8为剪切速率γ=.0、1、5、10 s-1时的相对结晶度发展。由图可知，由于剪切作用的存在，结晶速率将比静态条件下（0γ=.）的结晶速率有所增加，但这种增加在小剪切速率下（γ=.1 s-1）较微弱。同样，结晶的这种加速作用也是由剪切诱导的串晶所贡献的。

结晶形态的演化受剪切速率的影响与受剪切时间的影响类似。随着剪切速率的增加，串晶成核密度将有所增加，并且串晶的各向异性也更为明显。这里将不再作图显示，图形与图4类似。

2.4.2流体黏度的变化图9为不同剪切速率下流体黏度的变化。流体随时间的变化首先较为缓慢，但到某临界值时发生突增，这也是由结晶度所引起的。此外，剪切速率越大，流体黏度突增的时间点越早。这与Zheng等［9］的结果也是一致的。

图4　不同剪切时间下结晶形态的比较Fig.4　Morphology comparison with different shear time

3　结　论

本文给出了一个二维简单剪切流场下聚乙烯结晶过程的建模与模拟。基于Eder模型推导了球晶、串晶的形态演化模型；并用Zheng的两相悬浮模型描述聚合物流体，将体系的第一法向应力差作为串晶成核的驱动；与此同时，构建了模拟球晶、串晶形态演化的Monte Carlo法，分析了剪切时间、剪切速率对结晶速率、结晶形态、体系黏度等的影响。得出如下结论。

（1）本文所建立的Monte Carlo法合理有效，成功区分了晶体生长模式，捕捉了晶体生长前沿，较为直观地给出了晶体的演化发展；同时，统计获得了可信的相对结晶度。该方法的优势在于成功避开了使用结晶动力学模型，避免由结晶动力学模型中参数的不确定而导致预测的失真。

（2）剪切时间对结晶速率、结晶形态影响重大；剪切时间越长结晶速率越快，串晶对结晶形态的影响越明显，各向异性更为显著。剪切时间对流体黏度也有显著影响，这种影响主要体现在对结晶度的依赖上，当结晶度接近于某临界值时，体系黏度将发生突增现象。

（3）剪切速率对结晶速率、结晶形态、体系黏度等的影响与剪切时间的影响类似；增加剪切速率能提高结晶速率、提高串晶的各向异性以及使体系黏度发生突增的时间点提前。

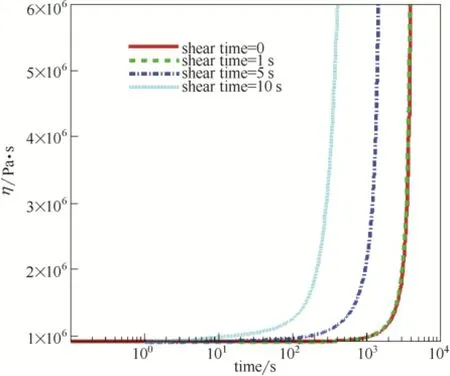
图5　不同剪切时间下流体黏度的变化Fig.5　Evolution of melt viscosity with different shear time

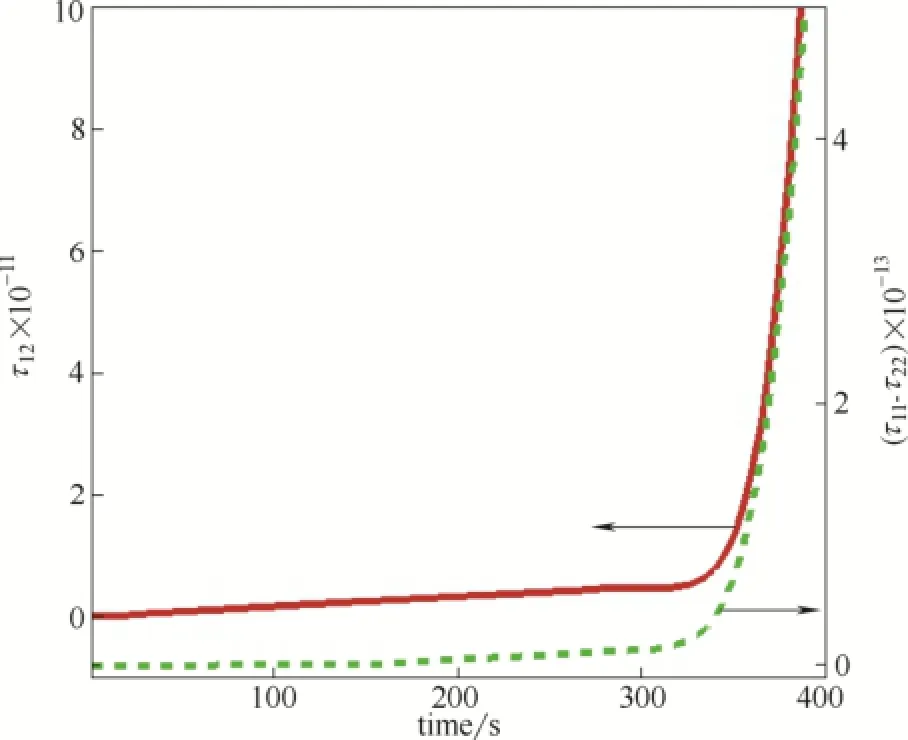
图6　剪切应力和第一法向应力差（剪切时间t=10 s）Fig.6　Shear stress and first normal stress （shear time t=10 s）

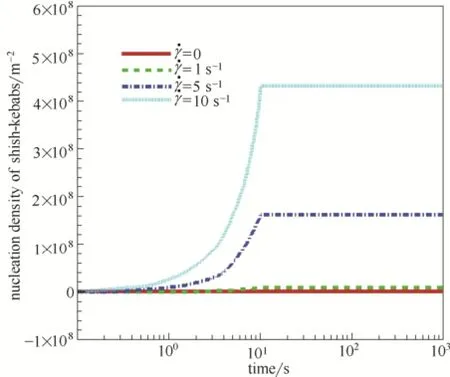
图7　不同剪切速率下的串晶成核密度Fig.7　Nucleation density of shish-kebabs with different shear rate

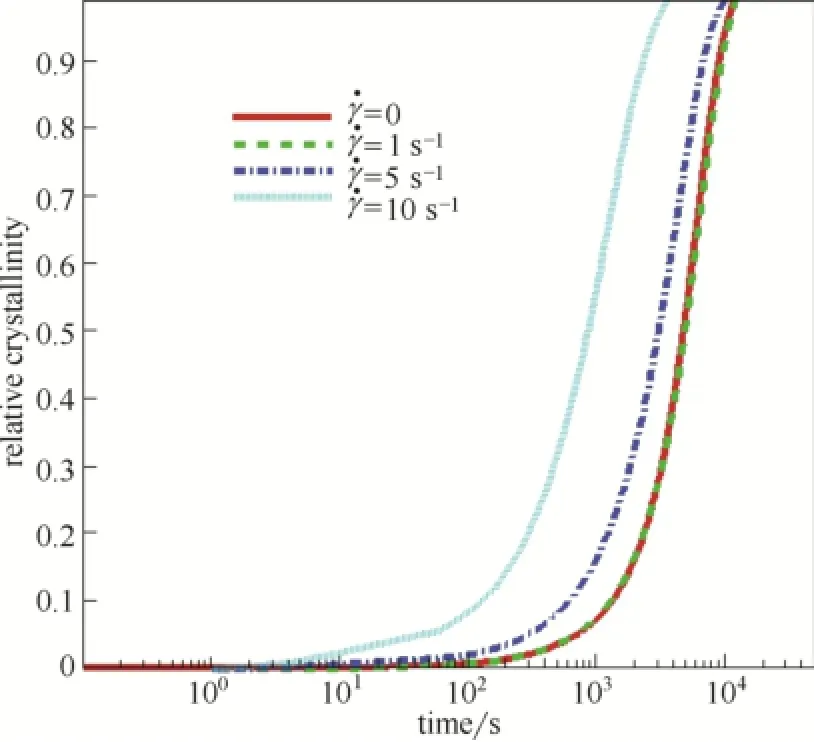
图8　不同剪切速率下的相对结晶度比较Fig.8　Relative crystallinity comparison with different shear rate

图9　不同剪切速率下流体黏度的变化Fig.9　Evolution of melt viscosity with different shear rate

符号说明

b——哑铃的有限拉伸参数

C——弹性哑铃构型张量，m

Gs，Gs-k，l，Gs-k，r——分别为球晶、串晶轴向、串晶径

向生长速率，m·s-1

Ns，Ns-k——分别为球晶、串晶成核密度，m-2

N1——第一法向应力差，N·m-2

R——刚性哑铃取向向量，m

T——热力学温度，K

t——时间，s

Δt——时间步长，s

α——相对结晶度

ηa，ηsc——分别为无定形相、半结晶相黏度，Pa·sa

λ，scλ——分别为无定形相、半结晶相分子

松弛因子时间，s

τ，aτ，scτ——分别为总体、无定形相、半结晶

相应力，N·m-2

∇——梯度算子

〈〉——系综平均

下角标

a ——无定形相

s ——球晶

s-k ——串晶

sc ——半结晶相

References

［1］KENNEDY P， ZHENG R. Crystallization//Flow Analysis of Injection Molds ［M］. Munich： MunichCarl Hanser Verlag， 2013： 141-153.

［2］ZHE M， LUIGI B， GIUSEPPE P， et al. Flow induced crystallization in isotactic polypropylene during and after flow ［J］. Polym.， 2014， 55：6140-6151.

［3］NAKAMURA K， WATANABE T， KATAYAMA K， et al. Some aspects of nonisothermal crystallization of polymers （Ⅰ）：Relationship between crystallization temperature， crystallinity， and cooling conditions ［J］. J. Appl. Polym. Sci.， 1972， 16： 1077-1091.

［4］KOLMOGOROV A N. On the statistic of crystallization development in metals ［J］. Bull. Akad. Sci. USSR， Class Sci.， Math. Nat.， 1937， 1：355-359.

［5］DOUFAS A K， MCHUGH A J， MILLER C. Simulation of melt spinning including flow-induced crystallization （1）： Model development and predictions ［J］. J. Non-Newtonian Fluid Mech.， 2000， 92： 27-66.

［6］TANNER R I， QI F Z. A comparison of some models for describing polymer crystallization at low deformation rates ［J］. J. Non-Newtonian Fluid Mech.， 2005， 127： 131-141.

［7］WO D L， TANNER R I， FLETCHER D F. A numerical treatment of crystallization in tube flow ［J］. Prog. Polym. Sci.， 2012， 56： 1356-1366.

［8］KOSCHER E， FULCHIRON R. Influence of shear on polypropylene crystallization： morphology development and kinetics ［J］. Polym.，2002， 43： 6931-6942.

［9］ZHENG R， KENNEDY P. A model for post-flow induced crystallization： general equations and predictions ［J］. J. Rheol.， 2004， 48： 823-842.

［10］EDER G， JANESCHITZ-KRIEGL H， LIEDAUER S. Crystallization processer in quiescent and moving polymer melts under heat transfer conditions ［J］. Prog. Polym. Sci.， 1990， 15： 629-714.

［11］ZUIDEMA H， PETERS G W M， MEIJER H E H. Development and validation of a recoverable strain-based model for flow induced crystallization of polymers ［J］. Macromol. Theory Simul.， 2001， 10：447-460.

［12］GUO X， ISAYEV A I， GUO L. Crystallinity and microstructure in injection modelings of isotactic polypropylenes （Ⅰ）： a new approach to modeling and model parameters ［J］. Polym. Eng. Sci.， 1999， 39（10）： 2096-2114.

［13］王锦燕， 陈静波， 刘春太， 等. 聚合物流动诱导结晶数值模拟 ［J］.化工学报， 2011， 62 （4）： 1150-1156. WANG J Y， CHEN J B， LIU C T， et al. Numerical simulation of shear-induced crystallization of polymer ［J］. CIESC Journal， 2011， 62（4）： 1150-1156.

［14］荣彦， 贺惠萍， 曹伟， 等. 基于两相模型的聚合物流动诱导结晶数值模拟 ［J］. 化工学报， 2012， 63 （7）： 2252-2257. RONG Y， HE H P， CAO W， et al. Numercial simulation of flow-induced crystallization of polymer based on two-phase model ［J］. CIESC Journal， 2012， 63 （7）： 2252-2257.

［15］ZHOU Y G， TURNG L， SHEN C Y. Modeling and prediction of morphology and crystallinity for cylindrical-shaped crystals during polymer processsing ［J］. Polym. Eng. Sci.， 2010： 1-10.

［16］杨玉良， 张红东. 高分子科学中的Monte Carlo方法 ［M］. 上海：复旦大学出版社， 1993. YANG Y L， ZHANG H D. Monte Carlo Method in Polymer Science［M］. Shanghai： Fudan University Press， 1993.

［17］AVRAMI M. Kinetics of phase change （Ⅰ）： General theory ［J］. J. Chem. Phys.， 1939， 7： 1103-1112.

［18］HOFFMAN J D， MILLER R L. Kinetics of crystallization from the melt and chain folding in polyethylene fractions revisited： theory and experiment ［J］. Polym.， 1997， 38： 3151-3212.

［19］NASIR A， MUHAMMAD A J， MUHAMMAD S. Theoretical analysis of the exiting thickness of sheets in the calendaring of FENE-P fluid ［J］. J. Non-Newtonian Fluid Mech.， 2015， 225： 28-36.

［20］ABOUHAMZEH M， SINKE J， JANSEN K， et al. Closed form expression for residual stresses and warpage during cure of composite laminates ［J］. Compos. Struct.， 2015， 133： 902-910.

Numerical simulation of morphology and kinetics of polyethylene in shear flow

RUAN Chunlei1，2， LIU Chuntai2
（1School of Mathematics and Statistics， Henan University of Science and Technology， Luoyang 471023， Henan， China；2National Engineering Research Center for Advanced Polymer Processing Technology， Zhengzhou 450001， Henan， China）

The mathematical model of morphology evolution of spherulites and shish-kebabs in the shear flow is deduced based on the Eder model. The model considers that the nucleation and growth of spherulites are determined by the static temperature， while the nucleation and growth of shish-kebabs are determined by the flow，which is depended on the first normal stress difference of the system and the shear rate respectively. In order to calculate the nucleation density of the shish-kebabs， the two-phase suspension model of Zheng is introduced. The model treats the stress as the combination of the amorphous phase and semi-crystalline phase. The amorphous phase is described by FENE-P model while the semi-crystalline phase is depicted by a rigid dumbbell model. Based on the mathematical model， the Monte Carlo method and the finite difference method are constructed，respectively. The former is to capture the crystal growth while the latter is to calculate the equation of the system. By using these methods， the 2D crystallization in the shear flow is simulated. The evolution of spherulites and shish-kebabs is given. Also， the effects of shear time and shear rate on the nucleation density of shish-kebabs，crystallization rate， the viscosity of the fluid and the system stress are discussed. Numerical results show that the Monte Carlo method is valid which not only captures the morphology evolution of crystals successfully， but alsopredicts the crystallization rate well. In addition， the increase of the shear time or the shear rate will increase the nucleation density of shish-kebabs and the crystallization rate.

date： 2015-09-21.

RUAN Chunlei， ruanchunlei622@mail.nwpu. edu.cn

supported by the National Natural Science Foundation in China （11402078， 51375148）.

flow induced crystallization； morphology； kinetics； Monte Carlo simulation； crystallization

O631.+3

A

0438—1157（2016）05—2144—08

2015-09-21收到初稿，2016-01-11收到修改稿。

联系人及第一作者：阮春蕾（1983—），女，博士，副教授。

国家自然科学基金项目（11402078，51375148）。