整体出发 事半功倍

薛秋萍



整体出发 事半功倍

薛秋萍

我们常说，在一个集体中一定要有整体观念，其实在数学问题的解决中，整体化的思想也是很重要的.从整体上把握解决问题的方向，往往可以寻找到突破口，避免繁杂的计算，收到事半功倍的效果.整体思想在本章中有广泛的应用，现举例说明.

一、整体思想在整式乘法中的运用

例1计算：（1）（x+y-1）（x+y+1）；

（2）（x-2y+z）（x+2y-z）；

（3）（a-2b+3c）2.

【分析】（1）中是两个三项式相乘，可以用乘法分配律进行运算，但比较麻烦.如将x+y看作一个整体，就可用公式；（2）中若把2y-z视为整体，那么-2y+z=-（2y-z）；在（3）中，只要先将a-2b整体作为一项，就可直接用完全平方公式.

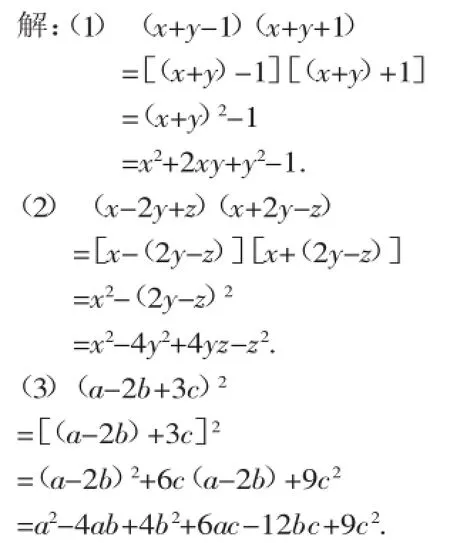
【反思】当相乘的多项式是两个三项式，且除了符号其他都相同时，可以“整体”地把符号相同的看作一“项”，把符号相反的看成另一“项”；应用（3）的方法，很快就能得到一个重要而实用的公式：

（a+b+c）2=a2+b2+c2+2ab+2ac+2bc

二、整体思想在因式分解中的运用

例2分解因式：（x2-2x）（x2-2x+2）+1.

【分析】若把两个二次多项式x2-2x、x2-2x+2相乘，则将得到一个四次多项式，这时再分解因式就十分困难.但若把x2-2x视为一个整体A，原式就变形为关于A的二次多项式，问题就容易解决了.

【反思】本题看似超出了学习的范围，但当把x2-2x看作整体时，就转化成了我们熟悉的二次三项式的简单分解.

同学们可依此法分解：（x+1）（x+2）（x+ 3）（x+4）+1.

【提示】先分别计算（x+1）（x+4）和（x+ 2）（x+3），问题就转变成了本例.

三、整体思想在求代数式值中的运用

例3（1）已知：x2-1=2x，求（x-1）（3x+ 1）-（x+1）2的值.

（2）已知：a+b=7，ab=12.

求：a2+b2，（a-b）2的值.

【分析】对于（1），把式子作适当变形后把x2-2x看作一个整体，求出x2-2x=1，再将其代入化简后的代数式很容易得到结果.

对于（2），要求代数式的值，最基本的思路是先求出a、b的值，但求解困难并使问题复杂化.如果我们对代数式先进行化简或变形，然后把a+b与ab看作一个整体，进行整体代入，则问题就会变得非常简单.

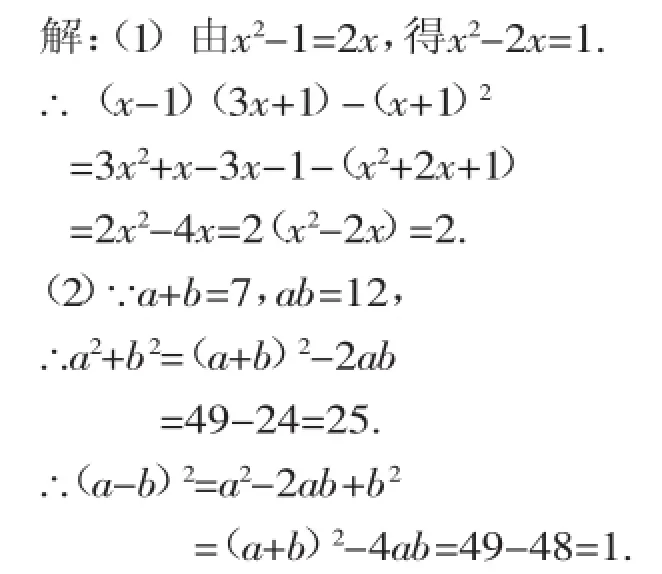
【反思】在（1）中，同样可以运用降次的思想，把x2-1=2x转化为x2=2x+1，再代入2x2-4x，得2（2x+1）-4x=2.

在（2）中，关键是将所给式用整体a+b、ab来表示.

这里用了常见的基本结论：

（a-b）2=（a+b）2-4ab或其变形.

例4（1）设a-b=3，b-c=-2，求代数式3（a-c）2+2（c-a）-5的值.

（2）已知a=2016x+20，b=2016x+19，c= 2016x+21，则a2+b2+c2-ab-bc-ac的值是多少？

【分析】（1）已知条件中有三个字母a，b，c，无法求出它们的具体值，而所求式只与a-c整体有关.故有：由a-b=3，b-c=-2得：

（2）若把a，b，c直接代入式子，计算十分烦琐.但从整体出发，可迅速得到：

a-b=1，a-c=-1，b-c=-2.

而所求式可用完全平方公式改写为：

【反思】两小题我们都是用“整体思想”来审视条件和结论（式子），并找到了它们的“联系点”，才使问题得到快速的解决.

（作者单位：江苏省太仓市第二中学）