源于课本 高于课本

薛秋萍



源于课本 高于课本

薛秋萍

课本中有些例题属于双基性例题，它主要是起巩固基本概念或公式，形成基本技能的作用.它形式简单，内容单一，但适当变式、延展，也会起到整合知识、归纳方法、培养技能、发展思维的作用.下面以“整式乘法与因式分解”中的两道例题为例，说明不少试题都“源于课本”，可以在课本中找到原型，但同时又“高于课本”.

原题1（苏科版教材七下第78页例题5第（1）题）

计算：（x-3）（x+3）（x2+9）.

【说明】这是一道计算题，两次运用平方差公式.

变式1计算：（x-1）（x+1）（x2+1）（x4+ 1）（x8+1）.

【说明】本题把上题的“3”变成“1”主要为了便于表达计算结果，再增加几个因式.经观察，发现规律，由（x-1）（x+1）得（x2-1），再由（x2-1）（x2+1）得x4-1，…根据最后一个因式（x8+1）得结果为x16-1.

变式2计算：（x-1）（x+1）（x2+1）（x4+ 1）…（x2n+1）.

【解析】把最后一个因式中x的指数由具体的数字改为字母，由变式1得结果是（x2n-1）（x2n+1）=x4n-1，渗透了特殊到一般的数学思想.

变式3试求：（2+1）（22+1）（24+1）…（232+1）+1的个位数字.

【说明】本题中把变式2中的字母x换成数字2，并且还不能直接应用平方差公式，需添加第一个因式（2-1），这样才能使用平方差公式计算其结果，最后研究结果的个位数字.

∵21=2，22=4，23=8，24=16，25=32，…

∴2的整数次幂的个位数字每4个数字为一个循环组依次循环.

∵64=16×4，

∴264的个位数字与24的个位数字相同.

∴原式的个位数字为6.

原题2（苏科版教材七下第85页例题5第（1）题）

把下列各式因式分解：x2+10x+25.

【说明】这是一道利用完全平方公式进行因式分解的例题，目的是熟悉关于因式分解的完全平方公式特点，并能熟练运用完全平方公式进行因式分解.

解：x2+10x+25=（x+5）2.

变式1把x2+y2+10x-4y+29写成两个完全平方式的和形式.

【说明】本题要进行适当分组，同时要把常数29拆成25与4的和.

【延展1】如果x2+y2+10x-4y+29=0，求x 和y的值.

【说明】本题根据完全平方式的非负性质，列方程求解.

【延展2】已知正整数a，b，c满足等式a2+ b2+c2+49=4a+6b+12c，试判断三条长分别为a，b，c的线段能否围成一个三角形.若能，请判断该三角形的形状；若不能，请说明理由.

【说明】本题是一个综合题，首先要利用等式性质，把等式左边配成三个完全平方式，再利用平方式的非负性和三角形的三边关系，得出结论.

解：∵a2+b2+c2+49=4a+6b+12c，

∴（a2-4a+4）+（b2-6b+9）+（c2-12c+36）=0.

∴（a-2）2+（b-3）2+（c-6）2=0.

∴a-2=0，b-3=0，c-6=0.

即：a=2，b=3，c=6.

∵2+3＜6，

∴三条长分别为a，b，c的线段不能围成一个三角形.

变式2“a2≥0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式.

例如：x2+4x+5=x2+4x+4+1=（x+2）2+1，

∵（x+2）2≥0，

∴（x+2）2+1≥1，

∴x2+4x+5≥1.

试比较代数式：x2-1与2x-3的大小.

【说明】比较两个代数式值的大小，通常用做差法，即先求出两个代数式的差，再对其配方，最后判断正负性.

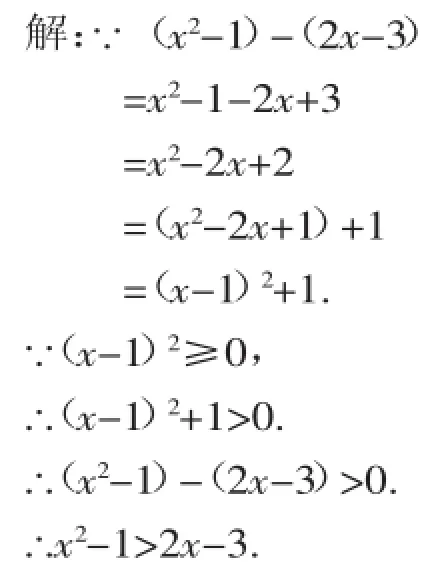
课本上的例题是我们学习的基础.同学们应多加重视，根据基本知识点，触类旁通，一题多变，做到学一题通一类，即使是最基础的计算题，我们也能使它生成新的题型，达到发展思维、培养能力的作用.

（作者单位：江苏省太仓市第二中学）