基于粗糙集理论的隧道围岩安全性影响因子研究

张小露 黄仕元 陈旺明

南华大学城市建设学院

基于粗糙集理论的隧道围岩安全性影响因子研究

张小露 黄仕元 陈旺明

南华大学城市建设学院

本文从文献资料中收集并整理多组隧道围岩分类数据，结合了粗糙集理论的数据挖掘功能和属性约简能力，建立了基于粗糙集理论的隧道围岩稳定性影响因子分析模型。对19组围岩数据系统进行属性约简后，在提取各属性等价类的基础上分别计算了属性重要度和权重，得出影响隧道围岩稳定性的因子的排列顺序，给隧道设计、施工提供了理论的依据和参考。

粗糙集；隧道；围岩；稳定性；权重

我国是一个地形复杂、人口众多的国家，随着经济的迅猛发展，地上空间已不足以满足人们生活需求，隧道的利用开发逐渐受到人们的重视。但是隧道事故的多发带来经济损失的同时还会造成人员伤亡。经专家分析影响围岩稳定性的因子有很多，它们之间关系复杂，相互还有一定的联系。目前，很多学者对隧道围岩的稳定性进行了深入的研究，主要表现为：利用智能方法对隧道围岩的稳定性进行预测，以及不确定理论对隧道围岩的稳定性进行评价［1］。

然而，由于围岩自身结构具有高度的非线性以及极强的不连续性，加之很容易受降雨、地震等自然因素的影响，主观的评价方法和复杂的数学计算往往难以反映出围岩的真实状态。为此，本文在深入研究前人成果的基础上，进一步引入了粗糙集理论，利用其强大的数据挖掘功能对隧道围岩系统中的数据进行规则提取，再计算出其属性的客观权重。

1　粗糙集理论

作为数据分析和数据处理的理论，粗糙集理论是在1982年由波兰科学家Z.Pawlak创立的［7］。粗糙集理论是一种新的处理模糊和不确定性知识的数学工具，其主要思想是保持相同的分类能力，得出分类规则。目前，粗糙集理论已成功地应用于机器学习，决策分析，过程控制，模式识别和数据挖掘等领域［2］。

2　基于粗糙理论的边坡稳定性属性分析

粗糙集理论是不需要提供历史数据以外的任何其它先验信息，即它能对给定的信息系统进行客观的描述，因此可将粗糙集理论作为前端数据处理器，一方面可以减少冗余，提高信息的有效性，另一方面它还能减少噪音的干扰，防止过训练和不收敛的现象［3］。采用粗糙集理论约简的流程，如下图。

图　粗糙集理论评价流程图

3　工程应用实例与分析

隧道围岩的稳定性直接关系到隧道的设计、施工、使用和维护。众多学者通过各种实验证明隧道围岩的稳定性与岩石力学性质、岩体构造及天然应力状态、地下水、开挖方式、支护方式等密切相关，但起到主要影响作用的是岩石完整性、地下水渗水量、岩体天然应力状态、岩石质量指标、地质构造［4-8］。可这五个影响因子的权重还未进行过分析，就不能在设计施工过程中有针对性的加强和巩固。根据《水工隧洞设计规范》及国内外围岩分类的经验，将围岩分为以下五种类别［9-14］，见表1。

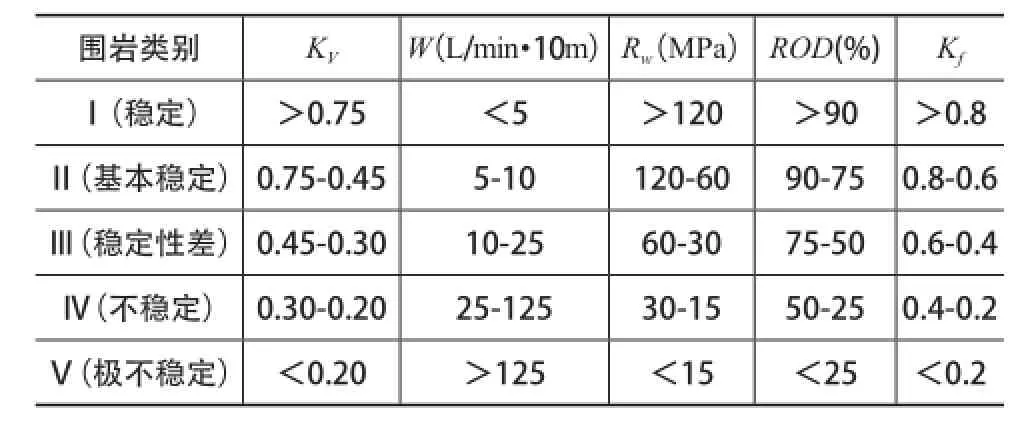
表1　隧道围岩分类

本文从文献中收集并整理了典型的边坡数据实例［11］，详细数据见表2，并列出了影响围岩稳定性的五个主要因素，分别为岩石完整性、地下水渗水量、岩体天然应力状态、岩石质量指标、地质构造，且在后文中分别用C1、C2、C3、C4和C5表示，F表示围岩类别，以此全部数据和信息作为此次粗糙集属性约简的原始数据。

表2　典型实例参数数据

3.1数据的离散化处理

应用粗糙集软件进行属性约简需要对原始数据进行离散化，一般采用等距离法进行处理，计算方法见公式（1），其中step=（max-min）/3表示每一列的步长。由于数据量较大，作者通过Matlab编程进行上述计算，将原始数据经过离散化处理后得到的结果，见表3。

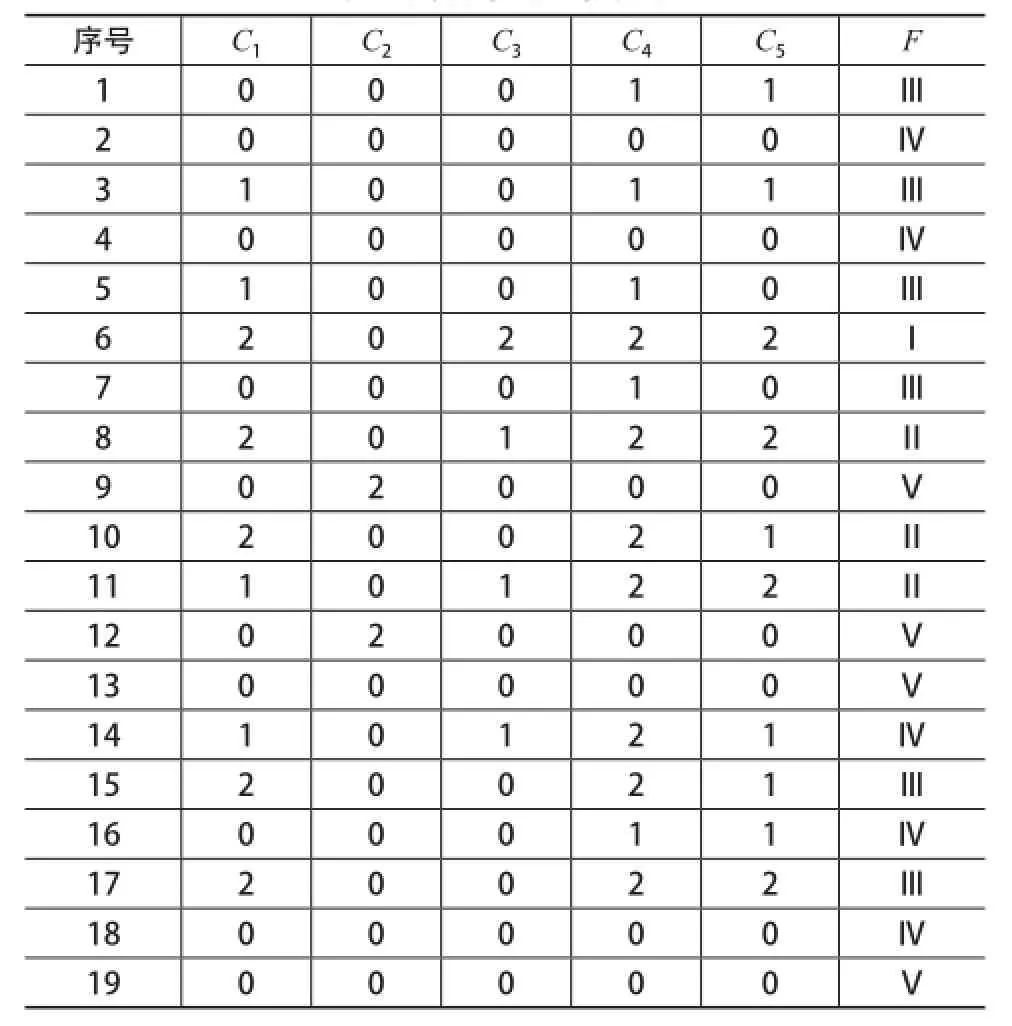
表3　离散化后的数据

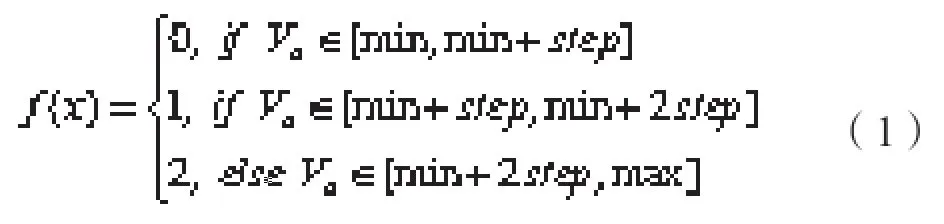
3.2基于粗糙集理论的围岩数据属性约简

属性约简是粗糙集理论研究的核心内容之一，它能保证在知识分类和决策能力不变的前提下，删除冗余信息。

属性约简的算法有很多，其各有优缺点，常用的有常规约简算法、可辨识矩阵约简算法、最大一致性因子约简算法等［2］。在粗糙集理论中的属性约简的方法主要是两种，一种是遗传算法（Genetic Algorithm），一种是穷举算法（Exhaustive Attack method），两种算法分别有它自己的特点和优点。本文分别采用穷举算法和遗传算法对评价指标属性进行约简，两种算法的约简结果，见表4、5。

表4　遗传算法的约简结果

表5　穷举算法的约简结果

由表4、5可知，遗传算法和穷举算法的约简结果一致，五个影响因子都能影响隧道围岩的稳定性，无冗余因素，且支持度都为100%。

3.3属性重要度计算

本组数据共计19组，用U=｛1，2，3…… 19｝表示，条件属性集C=｛ C1、C2、C3、C4、C5｝，决策属性集D=｛F｝=｛｛Ⅰ｝、｛Ⅱ｝、｛Ⅲ｝、｛Ⅳ｝、｛Ⅴ｝｝。

条件属性集的分类情况见表6，可知Card（U/C）=19；其中Card（U/C）表示集合｛U/C｝中元素个数；

决策属性集的分类情况见表7，可得Card（U/C）=19；

表6　条件属性集的等价类

表7　决策属性集的等价类

3.4属性的客观权重计算

上文中已计算出五个影响因子的属性重要度极其排列顺序，将各属性的重要度进行归一化处理即可得到不同属性的客观权重，计算方法如公式（2）所示。

因此，可得：

根据上述计算结果可知，结构面强度对隧道围岩的稳定性影响最大。因为围岩的结构和性质都是由结构面强度决定的，若围岩等级较低，可优先通过提高结构面强度来对围岩进行加固，会起到较好的效果。其次是岩石单轴饱和抗压强度，设法估算这种应力的大小并利用或消除未维护隧道围岩的稳定有着不可估量的作用。

4　结束语

一般情况下，属性权重的确定方法多是由决策者自己的先验知识决定的，如专家打分法等，但这种方法主观性太大。粗糙集理论是利用数据的特性，计算总结出各属性因子的客观权重，所得的结果更加客观。若能在用粗糙集理论计算客观权重的前提下，结合决策者的先验知识，得出属性因子的权重，将会对隧道围岩稳定性的预测提供更好的数据支持，也能在隧道后期的使用、维护、加固时，提供一个切入点和着重点，有利于围岩安全性的提高。

［1］ 赵彦辉，张乐文，邱道宏，等.基于粗糙集理论的隧道围岩模糊综合评价［J］.成都：四川建筑科学研究，2011，37（2）：125-128

［2］ 张文修，吴伟志，梁吉业，等.粗糙集理论与方法［M］.北京：科学出版社，2001

［3］ 曹秀英，梁静国.基于粗集理论的属性权重确定方法［J］.北京：中国管理科学，2002，10（5）：98-100

［4］ 宋笑雪.粗糙集理论及其应用［J］.咸阳师范学院学报，2005，20（2）：29-31

［5］ 李国辉，刘永，招国栋，等.基于RS-BPNN理论的边坡稳定性预测及应用［J］.衡阳［J］.南华大学学报，2015，29（3）：1-7

［6］ 张鹏，陈剑平，邱道宏.基于粗糙集的隧道围岩质量可拓学评价［J］.岩土力学，2009，30（1）：246-250

［7］ 李俊，薛质.一种基于粗糙集的安全评估方法［J］.信息安全与通信保密，2007，10（3）：89-91

［8］ 向仁军.基于粗糙集理论数据挖掘方法在边坡安全评价中的应用［D］.长沙：中南大学，2005

［9］ 刘刚，王国强.基于BP神经网络的隧道围岩稳定性分析［D］.合肥：合肥工业大学，2007，12：14-28

［10］ Polkowski L，Araszkiewicz B L.A Rough Set Approach to Estimating［J］.Elsevier，2009，（82）：32-44

［11］ Shen L，Loh H T.Applying Rough Sets to Market Timing Decisions［J］.Decision Support Systems，2004，（37）：583-597

［12］ Tsang E C，De gang C，Ye ung D S.Approximations and Reducts with Covering Generalized Rough Sets［J］.Computers and Mathematics with Applications，2008，（56）：25-37

［13］ Gaojun L，Yan Z.Credit Assessment of Contractors：A Rough Set Method［D］.Beijing：Tingshua University，2006

［14］ Tay F E，Shen L.Economic and Financial Prediction Using Rough Sets Model［J］.European Journal of Operational Research，2001，（141）：8-10