基于非对称质量损失函数的分段参数设计
卓德保,胥京波,张 浙
(上海师范大学 商学院,上海 200234)
在产品(或系统)质量设计中,产品性能和质量取决于产品各质量参数的组合。当质量参数相互独立时,各参数的最优即是产品整体性能和质量的最优;当质量参数间存在交互作用时,就要寻找各参数的最佳搭配关系,使得产品性能在此搭配关系下整体最优。参数设计是质量设计的重要内容,通过选择产品(或系统)中所有参数值(包括原材料、零件、元件等)的最优搭配水平,使其对随机因素的变化不敏感,从而抑制随机因素对系统输出质量的影响,达到系统输出质量波动小,稳定性好,成本低的目的。质量损失函数是通过描述系统在不同参数值下的损失,来度量系统质量偏离目标值而引起的经济损失。通常情况下,质量损失函数是围绕目标值的对称函数。但在实际中,损失函数并非一定是对称的,如果在规定的容许范围内,实际加工参数偏离目标值的方向不同,或偏离程度不同所造成的质量损失差别很大时,质量损失函数就会在目标值两侧形成非对称性。在电子产品、化学过程、切削工具的磨损过程、许多形状和位置误差的设计等,常常存在非对称现象。例如,在螺母的加工过程中,当实际加工的孔径参数值小于规格下限时,产品会造成返工损失;而孔径参数值大于规格上限时,会造成产品报废损失。这两种损失的不同,使得质量损失函数在目标值两侧是一边较平坦,另一边很陡峭,形成非对称质量损失函数。在电子产品方面,质量特性值高于或低于目标值时,产品散热、零件承受能力等因素会引发电子产品电阻等零件的变化,进而影响产品性能,使目标值两侧损失不同。如在热敏电阻产品中,电流等质量特性值高于目标值时产品产热过多,电阻变化较大,产品损失较大甚至失去功能;而质量特性值低于目标值时产品产热较少,电阻的温度变化较小,电阻变化不明显,产品损失相对较少,造成目标值两侧损失不对称的情况。
在这种情况下,采用对称质量损失函数的方法进行参数设计已经不合适,需要寻找一种非对称损失函数的度量方法,以便更精确的进行参数设计[1]。
实际研究中,许多学者在非对称质量损失函数和参数设计方面进行了研究,并取得了一定成果。非对称质量损失函数方面,陈本晶[2]提出了通过细分非对称质量损失函数的区间,分段求取各个小区间上的质量损失值的方法来解决非对称且不规则的质量损失函数的计算方法,这种方法为不规则的质量损失函数寻找到了解决方法,但其计算过程比较复杂,条件限制较多,且在2个端点质量损失值的确定上存在一定的不准确性;陈湘来等[3]在非对称损失函数的质量特性值优化选择中对不同情况下的质量损失进行分类讨论,并列举了特性指标值在规格界限内和界限外以及产品检验时3种情况的损失,并用MATLAB进行迭代计算,简化了计算难度;余慧敏[4]对一类非对称损失函数进行了最优不变估计,采用现有的非对称函数模型和单调变换群对质量损失进行计算,能精确计算非对称质量损失的值,但此种方法的局限性较大,只能适用于小部分数据。
在非对称损失函数的计算方面,研究最多的是用期望的方法求解。程岩等[5-6]基于非对称损失函数的参数设计中为2个质量损失系数建立损失系数比,将非对称质量损失函数的2个公式整合为1个,建立起一个非对称的质量损失函数式,而后通过求导的方式找到最优的参数,调整质量损失函数的目标值,进而减少产品损失,在非对称损失下威布尔分布的参数设计中用威布尔分布方程,讨论了在位置参数、尺度参数和形状参数3个参数的情况下,利用期望求质量损失的值;胡家喜等[7]在非对称损失函数正态分布总体的参数设计中考虑非对称质量损失函数,分别用一次和二次函数进行计算,而后用期望的方法进行参数设计;张晓勤[8]在n维非对称损失函数的参数设计中将非对称损失函数扩展到n维,讨论了在n维非对称的质量损失函数下,调整参数设计的可行性,求出质量损失的最小解,并以此进行了相关的参数设计;张斌等[9]在基于截尾正态分布的最优过程均值的确定中,讨论了在不对称田口质量损失函数下截尾正态分布的最优过程均值的确定问题,通过灵敏度分析,研究了过程参数对过程均值选择的影响。但非对称损失函数的期望的方法实际上是将非对称的质量损失函数做了一次对称化的变化,将两边的特性值做了一次折中处理,形成一个具有一定近似性质函数模型,这种方法能够非常方便地模拟出质量损失的值,但是获得的数据实际上是一个估计值,并不是一个具体的数值,故准确性偏小;其次,利用期望值进行参数设计时,只是调整了目标值,对产品特性值的均值的波动没有进行讨论,忽略了灵敏性设计时均值的不稳定性;最后,利用期望进行计算时,仅仅考虑了在机械元件中产品的特性值围绕目标值进行波动的情况,而对于电子元件中部分产品的特性值并不围绕目标值波动,需要进行产品特性值的迁移。
在非对称参数设计的研究中,许多学者提出了不同的方法,Wen等[10]讨论了过程受控但不满足规格限时过程均值的优化设计问题,Teeravaraprug等[11]提出运用回归分析的方法确定最优过程均值;Chen等[12]在质量特性分别服从正态、对数正态和指数分布的情况下,讨论了单边规格限的最优均值的确定问题;Lee等[13]讨论了基于田口对称损失函数的过程方差优化模型。
本文利用对质量损失函数分段的方法,解决非对称损失函数的参数设计问题。首先以目标值为分界点将非对称数据分为2个区间,假设每个区间的数据分别对应2个不同正态分布的一半,由此构造这2个不同的对称质量损失函数,再根据不同区间对应的质量损失函数进行参数设计。
1 非对称质量损失函数的构造
1.1 非对称质量损失函数的描述
质量损失函数的非对称性是由于过程输出参数落在目标值的上方和下方造成的质量损失率不同而形成的。故非对称质量损失函数都可用图1刻画。
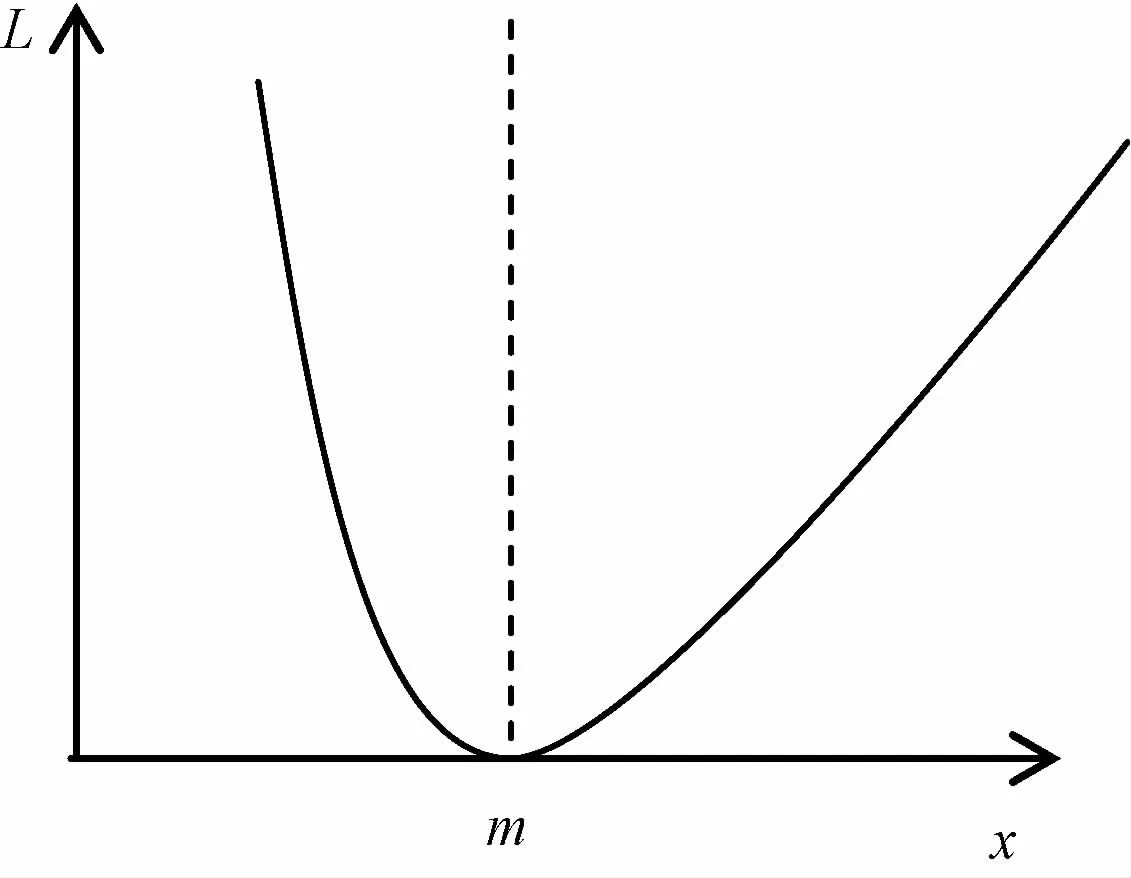
图1 非对称质量损失
图1中的m为目标值,假定质量特性值落在目标值上时,质量损失为0。可将图1分为2个区间:x≤m和x>m,x≤m区间的损失函数可假定为对称损失函数L1的左半部分,x>m区间的损失函数可假定为对称损失函数L2的右半部分,如图2 所示。将L1左半部分与L2的右半部分组合即可得到非对称方程的损失函数。

图2 非对称质量损失的处理分析
1.2 基于正态方法的非对称质量损失度量
在正态假设中,田口[14]认为产品的质量损失可以用质量损失函数来计算,通过泰勒展开,并假设质量目标值上损失为0的前提下,得出二次质量损失函数的计算公式,即

式中:L(x)为产品质量损失;k为质量损失系数;x为质量特性值;m为目标值,通过泰勒公式的变形,不难得出,其中,A0为输出质量特性为某一特定点时的质量损失值,Δ0为特定点的输出质量特性值偏离目标值的大小[14]。
而质量损失函数的期望值[15]为
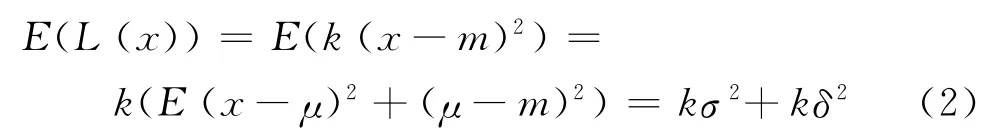
由式(2)可见,产品质量损失由两部分构成:
(1)σ2=E(x-μ)2,由质量特性值围绕均值的波动造成的损失,可通过减少标准差来增加产品的稳定性,即稳健性设计。
根据图2 的处理方法,构造非对称质量损失函数
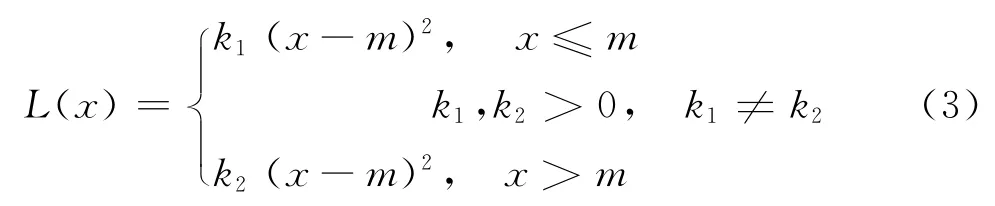
对于非对称损失函数,传统方法是将2个函数用1个损失系数进行整合,形成一个统一的公式,即令r=k2/k1,将其称为损失系数比[15]。则有
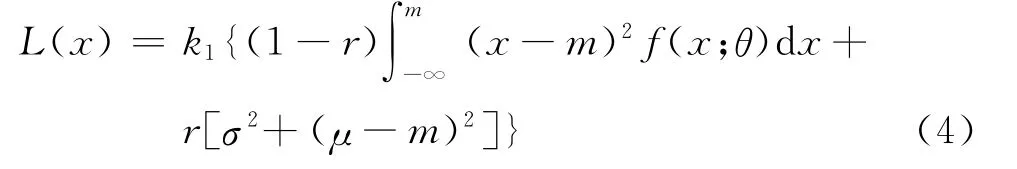
对于正态分布的曲线,其质量损失为
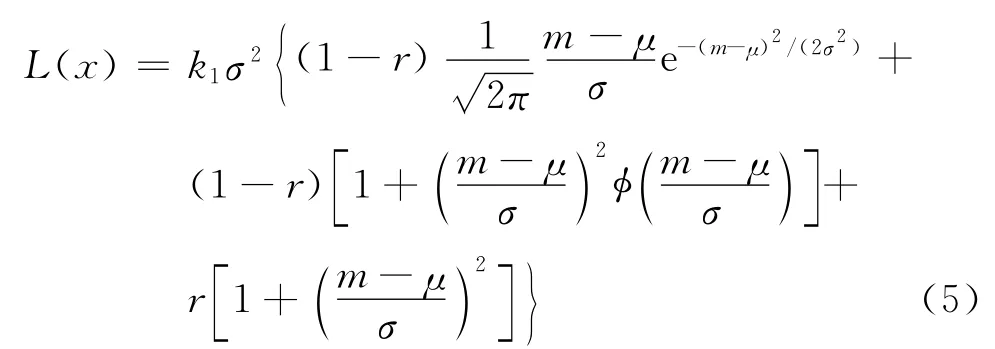
本文通过分段的方法进行质量损失的计算,通过分段质量损失加总的方法得到。其左侧及右侧的质量损失为:
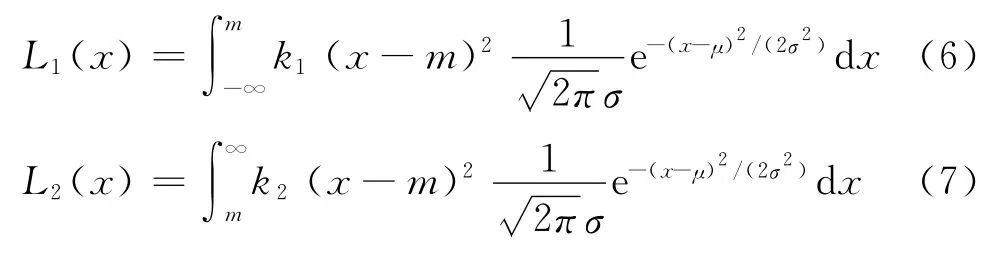
同时,将产品特性值分组,特性值小于m时用L1(x)计算损失,特性值大于m时用L2(x)计算损失,而后再将2个损失加和就是总的损失值,即
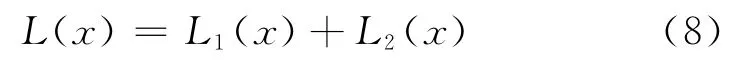
2 非对称情况下的分段参数设计方法
在分段质量损失计算的基础上,本文用分段计算的方法进行参数设计:
在L1(x)=k1(x-m)2的情况下进行参数设计,构造L1(x)=k1(x-m)2的方程保留其左侧并虚拟出方程对称的另一半曲线,将L1(x)=k1(x-m)2的定义域扩展到x∈(-∞,+∞),方程L1(x)=k1(x-m)2成为一个完整的二次曲线,L1(x)关于m对称。
此时,质量特性值x服从均值为μ,标准差为σ的正态分布,其密度函数为
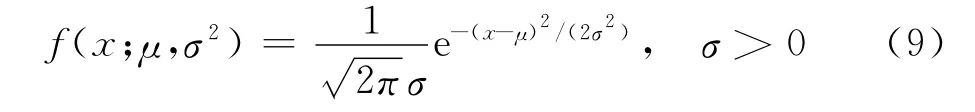
此时存在两种情况:
(1)当均值μ和目标值m重合时,产品的质量特性主要来自质量特性围绕均值的波动(本文称为第1类波动),此时,质量参数的设计主要采用减小此类波动的稳健性设计方法进行。
(2)当均值μ和目标值m不重合时,产品的质量损失一方面来自质量特性值均值偏离目标值的波动(本文称为第2 类波动),另一方面来自质量特性值围绕均值的波动(第1 类波动),质量参数的设计分两步进行:①采用与第1 种情况相同的稳健性设计方法,减小质量特性围绕均值的波动;②进行灵敏性设计,减小均值偏离目标值的波动。第2种情况存在均值左偏离目标值和均值右偏离目标值两种可能,如图3、4所示,此时需要寻找总体质量损失最小的均值点,并根据两种可能判断调整方向和大小。
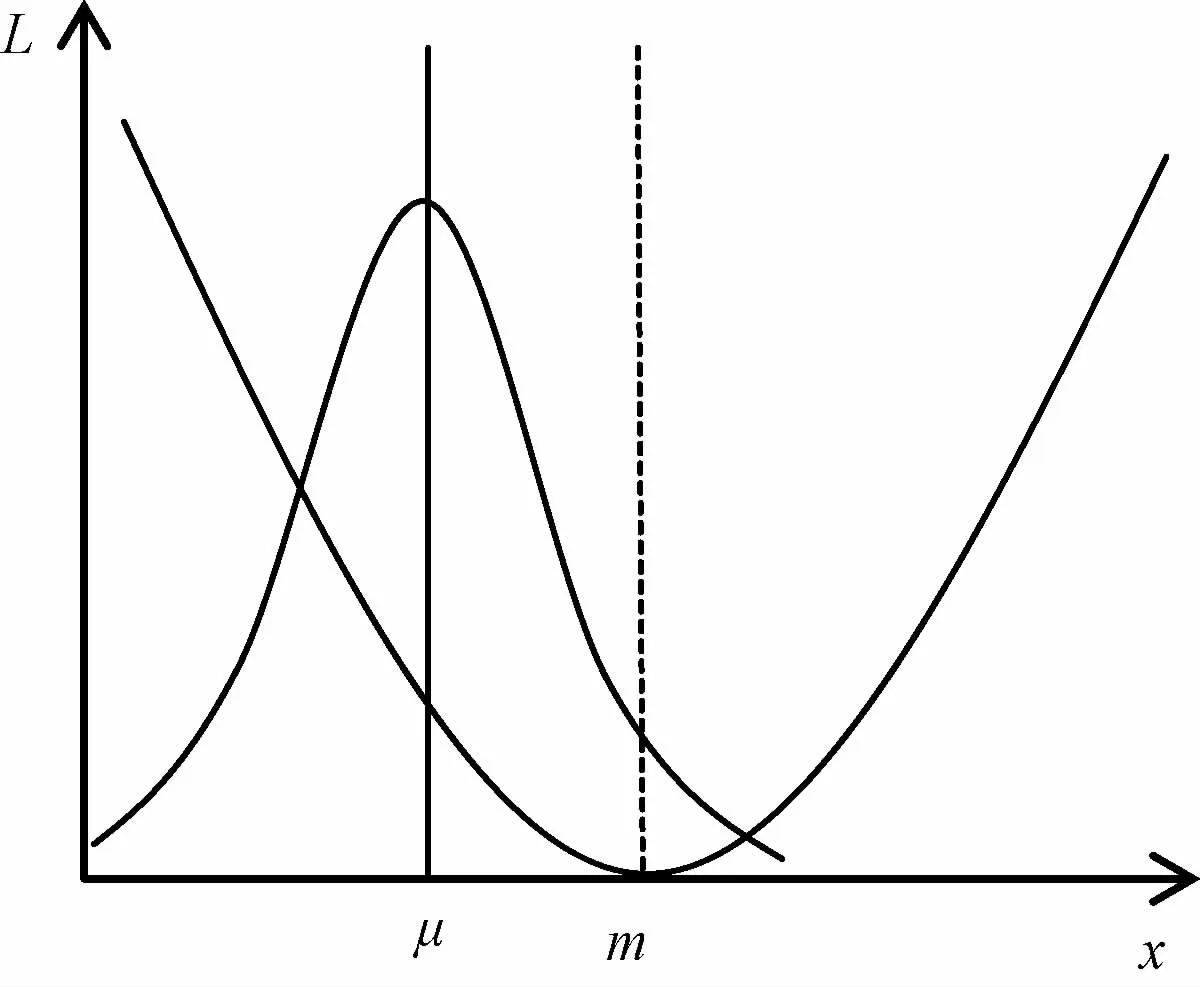
图3 均值向左偏离目标值
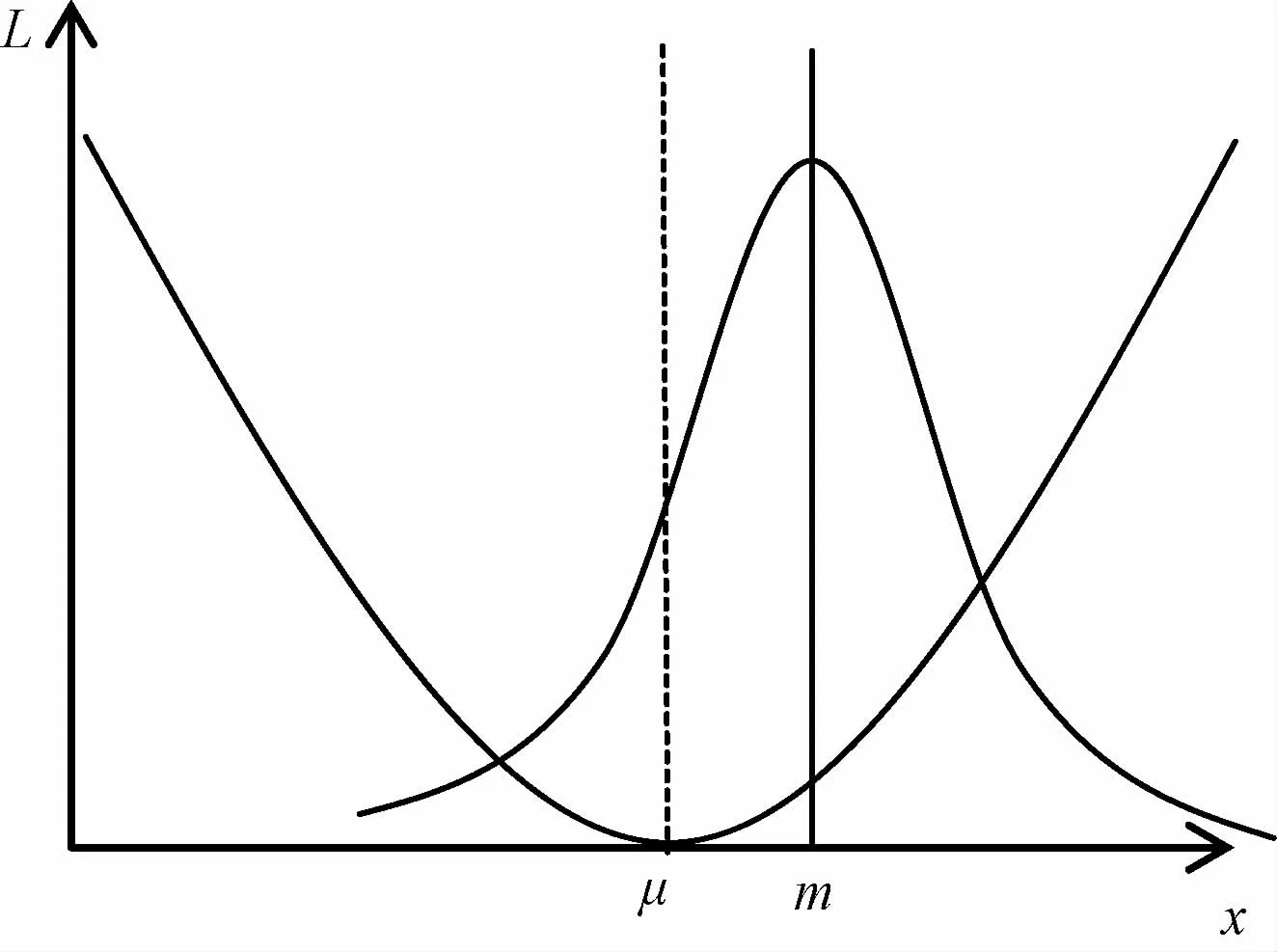
图4 均值向右偏离目标值
同理,运用相同方法进行L2(x)=k2(x-m)2的设计。本文对第2种情况进行设计。在进行参数设计时,判断产品的质量损失都来自于哪些方面的波动,如果两种波动都存在并造成损失,则需要通过稳健性和灵敏性设计减少两种质量损失。
2.1 稳健性设计
在稳健性设计的过程中,通过正交试验寻找质量参数的最优组合,以使输出质量特性值的波动最小。通过对每组参数组合的输出质量特性值进行信噪比计算,确定信噪比最大的参数组合为稳健设计中的最优参数组合。其信噪比计算公式为
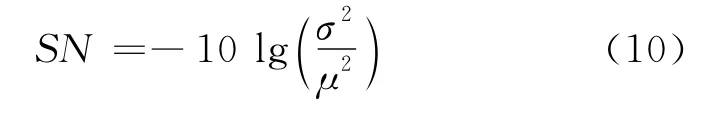
为了验证最优参数设计的合理性,需要对各组参数组合进行质量损失测算。将产品的特性值根据目标值分为目标值左侧的产品特性值以及目标值右侧的产品特性值两部分。对两侧的产品特性值分别计算质量损失,并将每个参数组合左右两侧的质量损失进行加和,如表1所示。求出总的质量损失之后,按照质量损失从小到大的顺序排列参数组合方案。总质量损失最小时对应的参数组合为稳健性设计中的最优参数组合设计。可以验证,在不存在第2类波动的情况下,质量损失最小的参数组合与信噪比最大的参数组合是一致的。

表1 产品特性值的损失计算图表
当存在第2类波动时,质量损失是最小的参数组合与信噪比最大的参数组合可能不一致。
2.2 灵敏性设计
在灵敏性设计中,首先是在稳健性设计的基础上利用环境因子,此处为噪声因子,测定在不同的外界条件下参数组合的敏感程度以及质量特性值均值的调整量δ。调整不同的噪声因子,并进行重复试验,输出不同噪声因子条件下质量特性值的均值。在此基础上,通过实验设计判断均值的稳定性,减少第2类波动造成的质量损失,而后计算总的质量损失,选择总质量损失最小的参数设计为最佳方案。
在非对称质量损失条件下,质量损失最小的均值μ未必就是设计目标值m。在调整输出质量特性均值的过程中,需要确定均值调整目标值μ*及调整方向和大小。
(1)均值调整目标值μ*的确定。根据质量损失的计算公式:
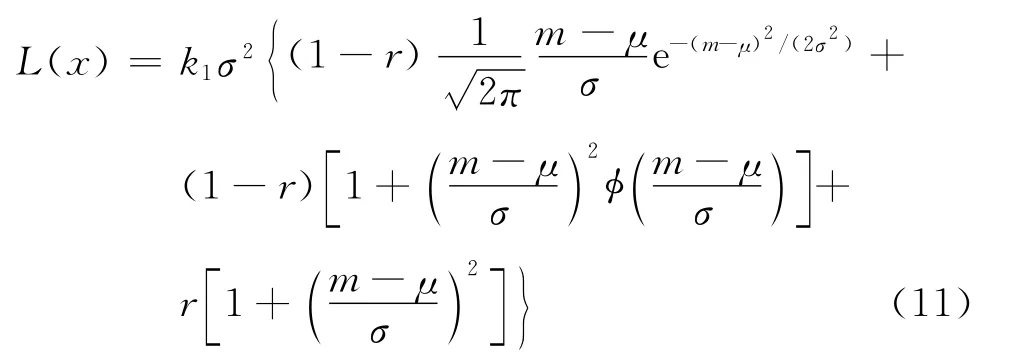
对其关于期望值进行求导,得
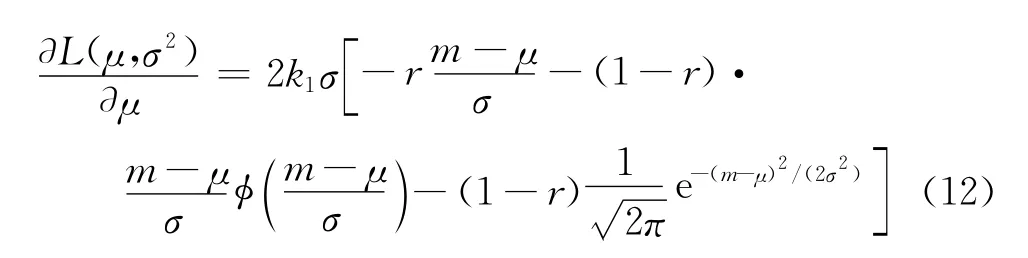
做变换λ=(m-μ)/σ,并称λ为调整参数。将其代入上式,可得
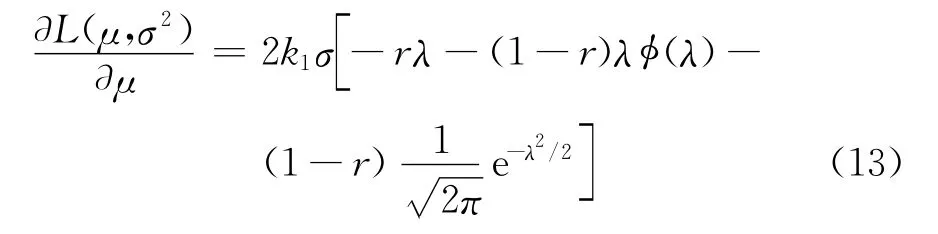
由式(13)可知,求解L(μ,σ2)的最小值,即求解∂L(μ,σ2)/∂μ=0时λ的值,分析可知,∂L(μ,σ2)/∂μ=0的解只与r有关,设质量损失L最小时λ的值为λ*,在质量特性波动最小的σ*下,使质量损失L(μ,σ2)最小的质量特性均值调整目标值为μ*,则满足:
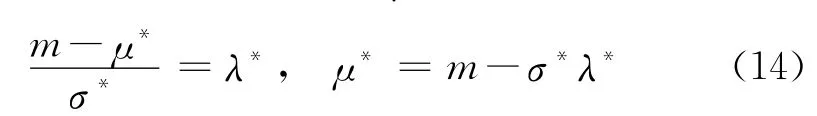
基于以上分析,需要找到损失系数比r与参数λ的函数关系,通过给出不同的r的值,计算∂L(μ,σ2)/∂μ=0,并计算对应参数λ的值。本文运用牛顿迭代法,得到r与λ的对应值,如表2所示。在实际应用中可通过查表直接引用。通过使用Matlab,可得r和λ的关系图,如图5所示。

表2 正态分布下最优调整参数表(r为损失系数比,λ为最优调整参数)
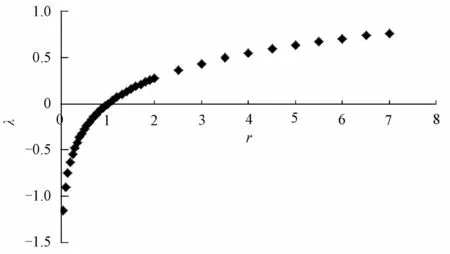
图5 r和λ 的关系
由此可知,如果非对称质量损失函数确定,则质量特性最佳均值调整目标值μ*(第2类波动带来的质量损失最小)就确定了。在非对称质量损失函数下,最佳均值调整目标μ*不等于目标值m,如图6所示。
确定最佳均值调整目标值μ*后,需要讨论在不同的外界环境下参数组合均值的波动问题。
对每种参数组合进行不同噪声因子条件下的试验,并多次重复,得到每种参数组合输出质量特性的均值μ,计算各组参数组合下不同噪声因子均值的均值和均值的方差,如表3所示。
其中,A、B、C、D 为相应的参数组合方案,μij为第i次重复试验下第j个参数组合输出质量特性的均值,为第j组参数组合的方差。
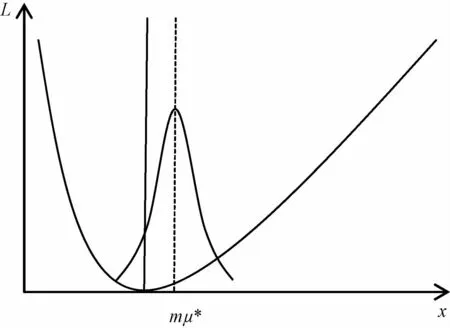
图6 最佳均值的确定
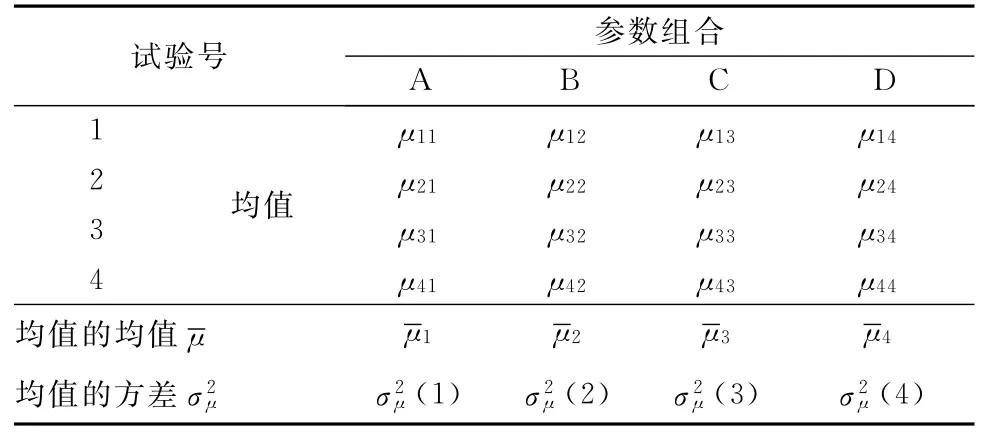
表3 多组试验参数组合的均值
(2)均值调整量Δ和调整方向的确定。当均值的均值与调整目标值μ*不重合时,可通过一定的技术手段找到与μ*的关系,确定调整量Δ的大小和方向,使均值的均值与均值调整目标值μ*重合。根据表3的计算结果。调整量
如表4所示。

4 多组试验参数组合的均值调整表
(3)确定调整后质量损失最小的参数设计方案。计算表4中均值调整后各参数组合下输出质量特性值均值的均值以及均值的方差。然后计算各参数组合下的信噪比。比较各参数组合下信噪比的大小,选取信噪比最大的参数组合,即为最优参数组合方案。
3 案 例
在电子产品的电路设计中,发现电子产品的输出质量特性值与其元器件参数的水平之间存在着非线性关系。质量特性值高于或低于目标值时,产品散热、零件承受能力等因素会引发电子元器件参数的非线性变化,使得参数偏离目标值的程度不同而带来目标值两侧的质量损失不同,形成不对称质量损失函数。现以电感电路的参数设计为案例来验证本文研究的参数设计方法。
电感电路由电阻R、电感L和一个电源组成,电阻R受热情况下电阻值会发生变化,导致电阻性能改变。当输入交流电压u和电源频率f时,输出电流强度
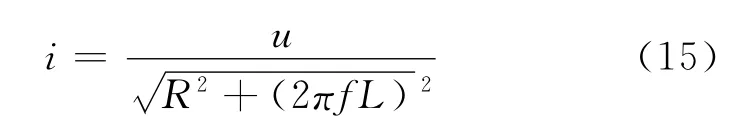
当电流强度围绕目标值上下波动时,电流产热会引发电感电路周边的温度发生变化,进而引发电阻R、晶体管等零件性能改变,使质量特性值在目标值两侧波动时产品的质量损失不对称。
通过分析产品生产过程中的材料损耗以及返厂维修、产品报废等数据,对产品的散热情况进行统计,并确定由于散热不及时导致返厂维修的费用,得出电流强度目标值两侧对应的质量损失函数为
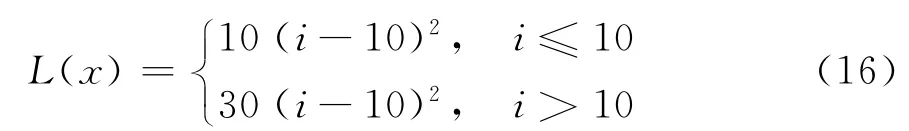
在输入电压u=100±10 V 和频率f=55±5 Hz的条件下,输出电流强度目标值im=10 A,由电流可确定电压u、电阻R、电感L和频率f的因子水平表,如表5所示。
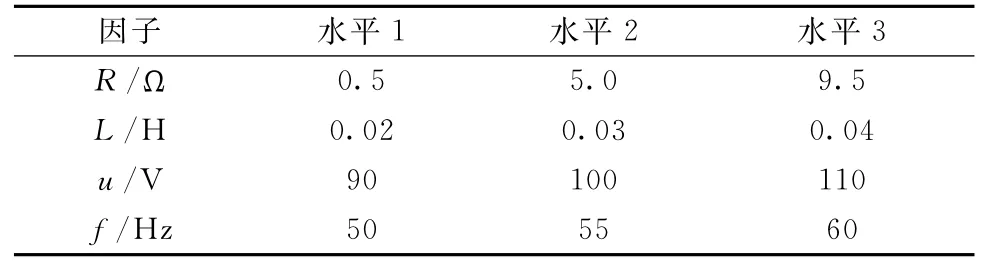
表5 因子水平表
将R和L的每个水平进行组合,而后进行重复试验,并利用数据进行正交实验,选取3水平正交表L9(34)进行试验,而后计算各组合的均值μ、方差σ2、信噪比SN以及质量损失L。并计算目标值im左右两侧的均值和方差,并求其信噪比SN,如表6所示。
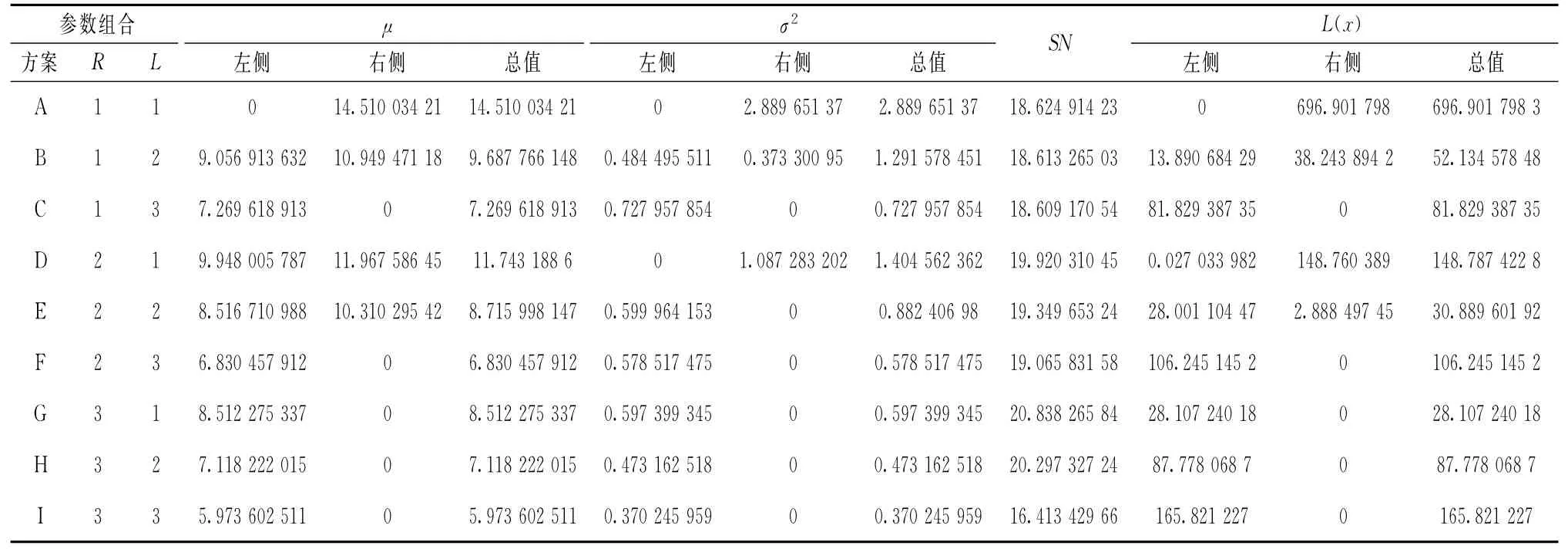
表6 目标值两侧均值、方差、信噪比及质量损失
比较各参数组合的信噪比可知,质量损失最小的参数组合与信噪比最大的参数组合相同,即为第G 组,所以,试验选取第G 组参数组合为最优参数组合。下一步进行灵敏性设计:
在均值调整目标值μ*的确定中,由于r=k1/k2=3,查表2得λ*=0.436 326 6。
选取第G 组参数组合下质量特性值的方差σ2*=0.597 399 345,由μ*=m-σ*λ*得到均值调整目标值μ*=9.739 339。
在均值的波动分析中,将供电电压u和供电频率f作为噪声因子,每组参数组合在不同的噪声因子条件下进行重复实验,得到各参数组合输出质量特性的均值,并计算各组参数组合下均值的均值和均值的方差。
参数R、L因子及噪声因子u、f的水平设置如表7所示。
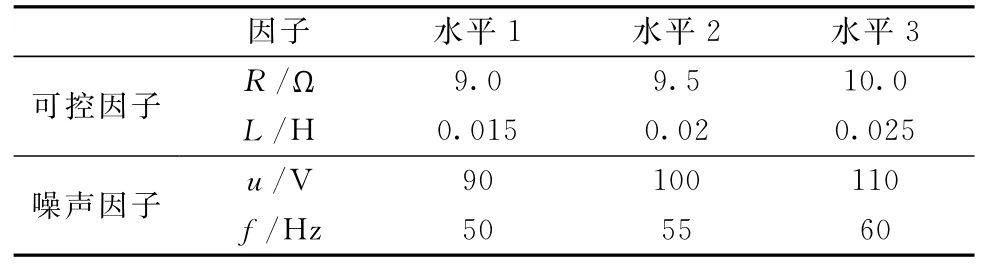
表7 考虑噪声因子的水平设置
可控因子(R,L)有9种组合,在每一种组合下,通过设计噪声因子并进行重复试验,此时,依然使用4因子3水平的正交表进行设计,即L9(34)。一次试验结束后,会得到一个均值μ和方差σ2。然后模拟不同的外界环境,调整不同的噪声因子并进行重复试验,共进行18组,此时可得到每一种参数组合下的一组均值,对其进行均值的均值和均值的方差的计算,具体数据如表8~10所示。由表中数据,传统的方法调整目标值后就完成了参数设计,得出的最优 参 数 组 合 为 第E 组(9.5,0.02),其 损 失L(x)=7.210 964 467。
而本文通过相关产品的电路等的设计,实现产品特性均值的移动,使均值的均值与目标调整值重合,其相应的移动量Δ=μ*-(m-σ*λ*),而后多次试验,通过调整参数,使均值的波动减小,结合上文稳健性和灵敏性设计,产品的质量波动达到最小,使其损失降到最低,同时,由于分段计算质量损失,函数式能准确地度量在电阻R影响下每一段的损失值,比较损失值的大小,判断损失最小的参数组合为第I组,即最优的参数组合为(10,0.025),质量损失L(x)=6.200 069 665。

表8 数据移动调整前的数据
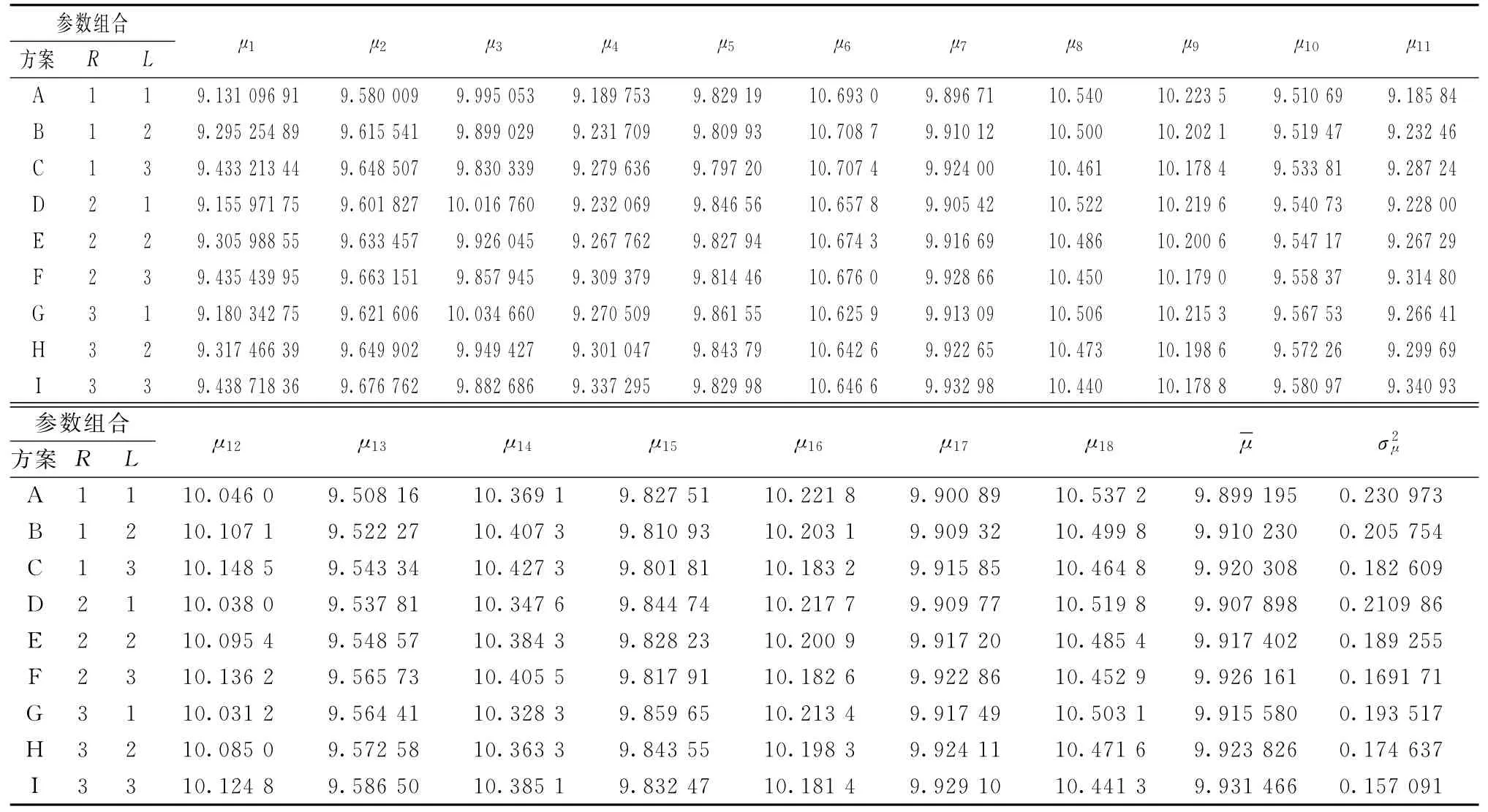
表9 数据移动调整后的数据
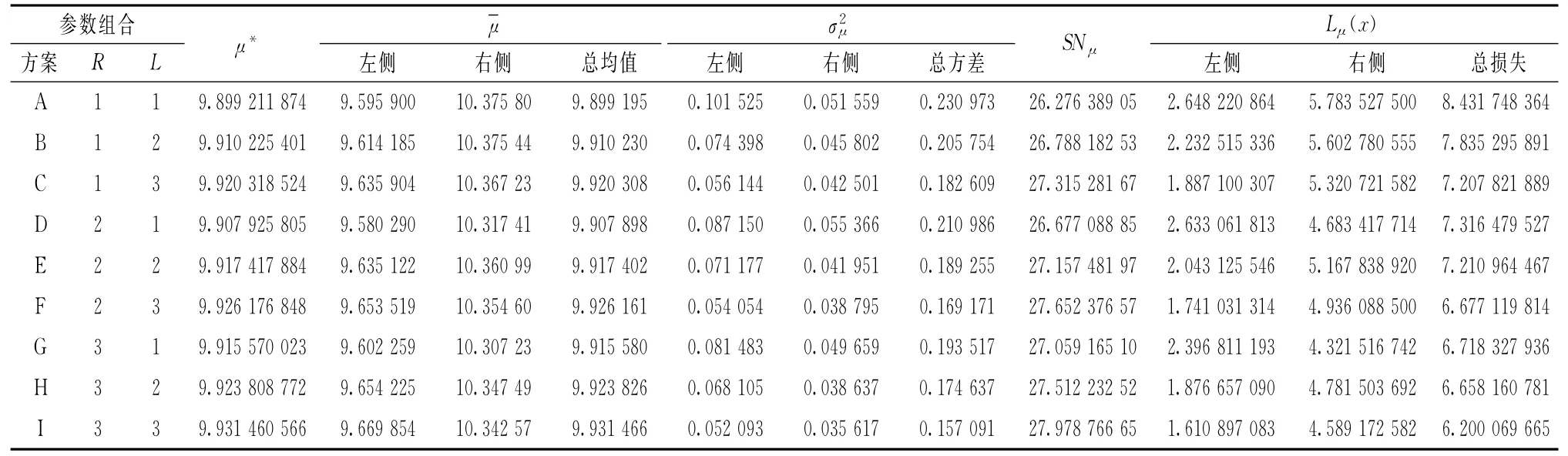
表10 调整后数值的运算列表
4 结语
在实际生活中,大量产品设计过程中质量特性值偏离目标值时,产品造成的损失并不对称,如果参数设计不合理,会给生产者以及社会带来不必要的损失。例如,随着智能手机的普及,其CPU 处理器在生产过程中就不得不考虑采用怎样的电阻及晶体管材料才能避免因散热原因导致的处理器性能下降和损失增加的问题。本文在非对称质量损失情况下,利用分段函数度量波动带来的质量损失,同时用正交试验进行参数设计,讨论了质量特性值对零件性能参数存在影响时,产品波动损失不对称的情况。首先进行稳健性设计,在正交实验设计中,通过信噪比确定稳健设计方案。并在稳健性设计的基础上进行灵敏性设计,以质量损失最小为目标,确定最优均值点,调整均值到最优值,再进行质量损失的分段计算,确定总质量损失最小的参数设计方案。本文在非对称质量损失函数情况下,利用分段函数度量质量损失的参数设计方案,还原了函数原有的形状,最直接的质量损失计算,提高了质量损失度量的精确性,以此为目标进行的质量参数设计方案更符合实际。

