SARAL测高卫星近海域波形重定新方法

李　静,岳建平,宋亚宏,彭刚跃

(河海大学地球科学与工程学院,江苏 南京　210098)



SARAL测高卫星近海域波形重定新方法

李静,岳建平,宋亚宏,彭刚跃

(河海大学地球科学与工程学院,江苏 南京210098)

利用AVISO提供的SARAL卫星浙江近海海域周年的WAVEFORM数据,通过对卫星波形分析,提出一种新的波形重定方法,该方法在顾及波形物理机制的基础上,根据各波形的特征进行重定。通过对重定前后的波形数据进行粗差剔除、共线平均和对比分析,结果表明:当纬度为27°左右时,未进行波形重定数据求得的平均海面高为10.770 m、标准差为4.515 m,而进行波形重定后数据求得的平均海面高为12.601 m、标准差为1.263 9 m;当纬度为30°左右时,未进行波形重定数据求得的平均海面高为12.236 m、标准差为1.877 m,而进行波形重定后数据求得的平均海面高为12.503 m、标准差为0.419 m。通过对波形重定前后卫星测高数据与验潮站数据对比,得到未进行波形重定的卫星测高数据与验潮站数据差值平均值为0.275 m、标准差为0.273 m,进行波形重定后卫星测高数据与验潮站数据差值平均值为0.046 m、标准差为0.049 m。研究结果显示利用本文提出的方法能显著提高卫星测高数据的精度与质量。

卫星波形重定技术;SARAL测高卫星;WAVEFORM数据;波形重定效果分析;浙江近海海域

卫星测高是伴随卫星遥感测量技术发展起来的新型边缘学科。它利用星载微波雷达测高仪,连续地向地面发射雷达脉冲,并接受来自海面返回的回波信号,实时测量卫星到海面的高度、有效波高和后向散射系数等,通过计算得到海面到参考椭球面的高度,进而为大地测量、地球物理学及海洋动力学提供研究资料[1]。SARAL是由法国CNES和印度空间研究所(ISRO)联合研制的测高卫星,于2013年2月25日发射升空,搭载altika测高计,并首次使用Ka波段[2]。其主要任务是执行精密重复的全球海面高、有效波高和风速等的观测,研究中尺度海洋变化、观测近海海域、内陆水域及大陆冰盖表面[3]。但是由于受到测高仪观测条件的限制,卫星测高技术的有效应用主要集中在深海海域。在靠近陆地的近海岸区域,由于测高仪的地面轨迹位于不同测量面交接面(例如海面与陆面、冰面与陆面等),其反射波形会发生变形,致使测高数据不可用,往往在预处理阶段即被剔除,因而在近海区域数据精度低甚至空白,影响了卫星测高数据在近海岸区域的实际使用效果。

本文采用AVISO提供的SARAL卫星浙江近海海域周年的WAVEFORM数据,通过对浙江近海海域SARAL测高卫星典型波形分析,旨在研究适合该区域的波形重定方法,提出一种新的波形重定方法,对近海岸波形进行波形重定。

1　波形重定新方法

测高卫星所观测的距离对应于接收回波脉冲最大振幅的50%,即为上升区的50%,通常称为前缘中点。卫星测高计在设计时通常预先设定某个时间点为波形的前缘中点,该时间点称为预设跟踪门。波形重定方法主要是用来确定波形实际的前缘中点和预设跟踪门之间的偏移量,然后根据公式计算出距离改正根据物理意义的不同,波形重定方法主要包括:β参数法、OCOG算法、Threshold及其改进算法、基于波形分类的重定算法等。β参数法采用适当参数函数对测高计波形进行拟合求得前缘中点位置。OCOG算法基于统计规律得到简单波形重定方法,其基本思路是找到每个返回波形的重心,以数值方式统计出波形振幅、宽度与重心位置,进而求出前缘中点。Threshold算法以OCOG算法作为计算基础,根据OCOG算法计算出的振幅大小,确定门槛值,在与前缘陡峭部分相交门槛的几个临近采样值之间进行线性内插,以确定重定点。基于波形分类的重定算法根据波形相似性进行分类,然后进行波形重定[4-9]。

1.1波形分析

测高雷达回波形状是卫星雷达测高计的基本观测量,是一个双向传播时间的函数,与反射面的散射特性密切相关。海洋面是一个平缓的、均匀展散的水面,对卫星雷达脉冲具有较好的反射特性[10]。在开阔的深海区域,卫星测高波形受陆地、岛屿、水底地形起伏、地球物理和硬件响应等因素影响很小,其波形形状能反映海洋面状况的特征,遵循布朗模型,海洋波形如图1所示[11]。当卫星地面轨迹靠近陆地时,由于其散射特性不同于海洋面,回波发生变形,如图2所示。

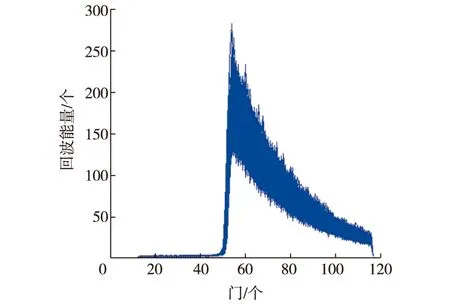
图1　海洋波形Fig. 1　Sea waveform

图2　近海域波形Fig. 2　Offshore waveform

由图1可以看出,典型的海洋测高波形包括热噪声区、前缘和后缘3部分。由图2可以看出,近海区域回波发生明显变形,规律性较差。

对浙江近海海域典型波形分析:图3中,第一类波形,系靠近岛屿下干山附近,距离陆地约13 km,其在上升缘之前有明显的单尖或多尖锥波形,分析其原因是卫星脉冲触及岛屿地面,能量被部分反射所致,但可看出波形具有明显的上升缘,可进行波形重定。第二类波形,系位于120.87°E,27.82°N,该点距离陆地约4 km,其波形虽被污染,但具有明显前缘,可进行波形重定。第三类波形,系位于灵昆岛两侧,可以看出波形已经发生严重污染,分析原因是水域较浅,波形受到陆地与水底影响,不可进行波形重定。第四类波形,系位于杭州湾靠近海黄山验潮站,该点位于陆地,可以看出已经完全没有海洋波形的形状,故不可进行波形重定。

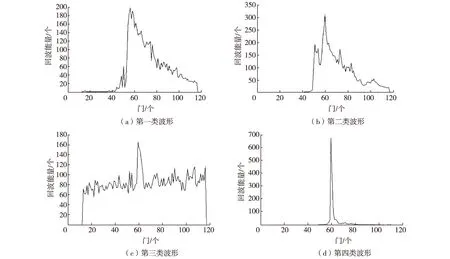
图3　SARAL测高卫星典型波形Fig. 3　SARAL altimetry satellite typical waveforms

1.2波形重定方法

在顾及波形物理机制基础上,根据各波形的特征进行重定。SARAL卫星每个波形有128个门,根据大量波形分析,总结出SARAL卫星的有效回波前缘一般集中在第40～60号门之间,前缘中点一般在52～53号门之间。基于此,若波形在热噪声区域已经发生严重变形(第三类波形),即回波能量值普遍高于所设定阈值,则对此数据进行剔除[12-15]。若波形呈现尖锥状(第四类波形),即回波能量有明显升高,但没有有效后缘,即进行如下判断:在波形能量连续上升的过程中,回波能量大于所设定阈值,且与前面2个门所对应平均能量值的比值和后面2个门所对应平均能量值的比值的和的平均值大于设定阈值时,认为此波形为尖锥状,对此数据进行剔除。如式(1):

(1)

式中:i——门号;P(i)——第i号门对应的回波能量;T1、T2——设定阈值。

针对第一类与第二类波形,进行如下操作求取前缘中点:当波形能量大于设定阈值且连续上升达到最大值时,由此向前寻找前缘中点,即当前波形能量的2倍与其前后波形能量求差值的绝对值,小于当前波形能量时,向前迭代,直到不满足条件,且需找到与最大能量值的1/2最接近的能量值所对应的门,即为前缘中点。如式(2):

(2)

式中：T3——设定阈值。

根据所求前缘中点与预设门求得改正量:

(3)

式中:ΔR——所求改正量;Gr——所求前缘中点;G0——预设门;ΔR0——总阈门间的距离。

2　实际效果分析

对重定前后的波形数据进行粗差剔除、共线平均,并进行对比,结果如图4所示。为便于观察,对图4中未重定数据整体上移1 m。

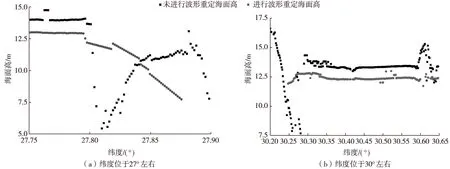
图4　进行波形重定前后数据对比结果Fig. 4　Comparison of data before and after waveform retracking

由图4(a)可以看出,未进行波形重定数据的趋势性不明显,且存在明显粗差,而进行波形重定后的数据在纬度27.8°以后呈现下降趋势,分析原因是随着纬度升高,由海洋向陆地过渡,故海面高呈现下降趋势;由图4(b)可以看出,未进行波形重定数据在纬度30.3°附近,由陆地向海洋过渡时存在明显粗差,在经过岛礁(纬度30.6°附近)时海面高有明显波动,而进行波形重定后的数据趋势性较好,且波动较弱。图4(a)中未进行波形重定的数据求得的平均海面高为10.770 m、标准差为4.515 m,而进行波形重定的数据求得的平均海面高为12.601 m、标准差为1.264 m;图4(b)中未进行波形重定的数据求得的平均海面高为12.236 m、标准差为1.877 m,而进行波形重定的数据求得的平均海面高为12.503 m、标准差为0.419 m,可见进行波形重定后数据质量明显提高。将测高数据与验潮站数据对比,结果如下:下干山、海黄山、滩浒山验潮站进行波形重定后的测高数据与验潮站数据的差值分别为0.111 m、0.003 m、0.025 m,未进行波形重定后的测高数据与验潮站数据的差值分别为0.153 m、0.019 m、0.653 m。可以看出:未重定的测高数据与验潮站数据差值平均值为0.275 m、标准差为0.273 m,进行波形重定后的测高数据与验潮站数据差值的平均值为0.046 m、标准差为0.049 m。以上结果表明进行波形重定后的测高数据更接近验潮站数据,本文的波形重定方法有效。

3　结　　论

利用AVISO提供的SARAL卫星浙江近海海域周年的WAVEFORM数据,通过进行卫星波形分析,探讨一种新的波形重定方法,对近海岸波形进行波形重定。通过对重定前后的波形数据进行粗差剔除、共线平均和对比分析,得到重定后数据质量得到提高。通过对波形重定前后测高数据与验潮站数据对比,得到未进行波形重定的测高数据与验潮站数据差值的平均值为0.275 m、标准差为0.273 m,进行波形重定后的测高数据与验潮站数据差值的平均值为0.046 m、标准差为0.049 m,表明采用波形重定技术能显著提高卫星测高数据精度,本文研究的波形重定方法有效,为提高近海平均海面精度以及深度基准面的精度提供了新的方法。

[1] 翟国君,黄谟涛,谢锡君,等.卫星测高数据处理的理论与方法[M].北京:测绘出版社,2000.

[2] AVISO. AltiKa, a Ka-band altimeter, Technical data[EB/OL].[2015-06-19]. http://www.aviso.altimetry.fr/en/home.html.

[3] AVISO. SARAL/AltiKa products handbook [EB/OL].[2015-06-19]. http://www.aviso.altimetry.fr/en/data.html.

[4] 李静, 岳建平,梁子亮. Jason-2卫星波形重定技术在研究贝加尔湖水位中的应用[J]. 河海大学学报(自然科学版), 2015,43(2): 163-166. (LI Jing, YUE Jianping, LIANG Ziliang. Application of Jason-2 waveform retracking method to investigation of wate level of Lake Baikal[J] Journal of Hohai University(Natural Sciences),2015,43 (2): 163-166. (in Chinese).)

[5] 高永刚,郭金运,岳建平.卫星测高在陆地湖泊湖面高变化监测中的应用[J]. 武汉大学学报(信息科学版),2008,33(6):73-75. (GAO Yonggang,GUO Jinyun,YUE Jianping. Lake level variations measurement with satellite altimetry[J].Geomatics and Information Science of Wuhan University, 2008,33(6):73-75. (in Chinese))

[6] 杨乐,林明森,张有广,等. 基于波形分类和子波形提取的雷达高度计近海波形重构算法[J].中国科学(地球科学), 2011(11): 1706-1713. (YANG Le, LIN Minsen, ZHANG Youguang, et al. A retracking algorithm based on waveform classification and sub-waveform extraction for coastal altimetry[J].Scientia Sinica Terrae, 2011(11): 1706-1713.(in Chinese))

[7] BAO Lifeng, LU Yang, WANG Yong. Improved retracking algorithm for oceanic altimeter waveforms[J]. Progress in Natural Science, 2009(2): 195-203.

[8] 孙佳龙. 近海雷达卫星测高数据质量改善及在南海海潮模型中的应用研究[D].青岛:山东科技大学,2011.

[9] 焦明连,孙佳龙. 基于聚类分析的多子波优化重定算法[J].海洋测绘,2013(6):36-38. (JIAO Minglian,SUN Jialong. A multi-wave optimized retracking method based on cluster analysis[J].Hydrographic Surveying and Charting,2013(6):36-38. (in Chinese))

[10] 郭金运,常晓涛,孙佳龙,等.卫星雷达测高波形重定及应用[M].北京:测绘出版社,2013.

[11] AVISO/Altimetry. AVISO and PODAAC user handbook IWAVEFORM and WAVEFORM Jason products [EB/OL].[2015-06-19]. http://www.aviso.altimetry.fr/en/data.html.

[12] AVISO. The Jason-2 mission [EB/OL].[2015-06-19].http://www.altimetry.info/html/missions/jason2/welcome_en.html.

[13] AVISO. Instruments[EB/OL].[2015-06-20]. http://www.aviso.altimetry.fr/en/missions/present-missions/saral.html.

[14] 浙江省人民政府.浙江[EB/OL].[2014-10-11].http://baike.baidu.com/view/4150.htm?fr=aladdin.

[15] 周浩,汪海洪,罗志才,等.基于动态聚类分析的卫星测高波形分类[J]. 大地测量与地球动力学,2011,31(5): 101-105.(ZHOU Hao,WANG Haihong,LUO Zhicai,et al. Classification of satellite altimeter waveforms based on dynamical cluster analysis[J]. Journal of Geodesy and Geodynamics, 2011,31(5): 101-105. (in Chinese))

A new method of offshore waveform retracking using SARAL altimetry satellite

LI Jing, YUE Jianping, SONG Yahong, PENG Gangyue

(SchoolofEarthScienceandEngineering,HohaiUniversity,Nanjing210098,China)

Using the annual WAVEFORM data of the Zhejiang offshore area from the SARAL satellite provided by AVISO, we analyzed the satellite waveform and proposed a new method of waveform retracking for offshore areas. With this method, a waveform was retracked according to its characteristics based on the physical mechanism. Through gross error elimination, collinear averaging, and comparison analysis of the waveform before and after retracking, we found that at 27° latitude around, the mean sea level drawn from raw data was 10.770 m, and the standard deviation was 4.515 m; the mean sea level drawn from retracked data was 12.601 m, and the standard deviation was 1.263 9 m. Around 30° latitude, the mean sea level drawn from raw data was 12.236 m, and the standard deviation was 1.877 m; the mean sea level drawn from retracked data was 12.503 m, and the standard deviation was 0.419 m. We compared the altimetry data with tidal gauge data, and obtained the following results: the mean difference between the raw data and tidal gauge data was 0.275 m, and the standard deviation was 0.273 m; the mean difference between the retracked data and tidal gauge data was 0.046 m, and the standard deviation was 0.049 m. The results show that the method discussed in this paper can greatly improve the accuracy and quality of satellite altimetry data.

waveform retracking with satellite; SARAL altimetry satellite; WAVEFORM data; waveform retracking effect analysis; Zhejiang offshore area

1000-1980(2016)04-0335-05

10.3876/j.issn.1000-1980.2016.04.009

2015-07-02

李静(1992—),女,山东菏泽人,硕士研究生,主要从事卫星大地测量研究。E-mail: hhu_lj@sina.com

P228

A