制造与装配误差对圆柱滚子轴承接触应力的影响

王秋志，蒋　玮，刘华汉

(大连理工大学机械工程学院，辽宁大连116024)



制造与装配误差对圆柱滚子轴承接触应力的影响

王秋志，蒋玮，刘华汉

(大连理工大学机械工程学院，辽宁大连116024)

在ABAQUS中建立了某型号圆柱滚子轴承在120 kN径向力作用下的静力学有限元模型，并用赫兹弹性接触理论验证了模型的正确性。首先采用有限元方法分析了轴承在无误差时的接触应力分布，接着分析了轴承存在游隙、滚子直径等制造误差和内外圈相对偏转等装配误差时轴承接触应力的分布规律和最大接触应力的变化趋势。分析结果表明，轴承在较小的负游隙时接触应力值较小；滚子直径偏离公称尺寸过大或过小都会引起接触应力异常增大；内外圈不同的相对偏转方式对接触应力产生的影响不同，研究结果对于通过提高制造质量以提升轴承的服役性能具有一定的指导意义。

圆柱滚子轴承接触应力游隙滚子直径偏转

0　引言

风能作为一种可再生的绿色能源越来越受到重视，促进了风力发电技术的商用化。增速箱是风力发电机组故障率最高的部件，而增速箱的故障大多是出现在轴承零件[1]。轴承在制造和装配过程中，由于设备和人为的原因，不可避免地会出现各种各样的误差，如轴承游隙的变化、滚子直径误差、轴承内外圈相对偏转等，这些误差都会对轴承的正常工作造成一定影响。因此分析这些因素对轴承工作状况的影响规律是必要的，可通过总结可控制的误差范围用来指导生产实践。

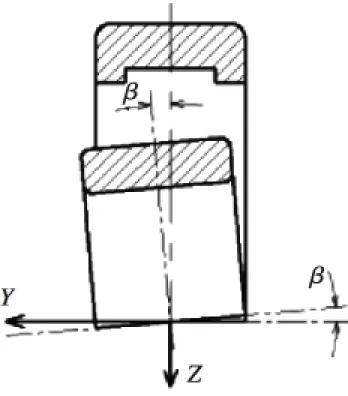
图1　内圈相对外圈绕X轴偏转

轴承游隙是指将轴承内圈或者外圈一方固定，然后使轴承未被固定的一方做径向或者轴向移动时的移动量。根据移动方向，可分为径向游隙和轴向游隙，对于圆柱滚子轴承，本文所指的游隙均特指径向游隙。在制造过程中，每个滚子的直径都或多或少地存在制造误差，为此在装配滚子时需要对滚子按照其实际直径的大小进行有规律的排布。轴承安装时，轴承内圈与轴过盈配合，外圈与轴承座过盈配合，轴与轴承座轴线不平行则会引起轴承内外圈的相对偏转，造成内外圈倾斜，如图1所示。上述制造和装配误差都将对圆柱滚子轴承接触应力的分布乃至服役性能产生影响。

国内外学者已经做了轴承误差方面的大量工作，文献[2]使用ANSYS方法分析了轴承内外圈滚道上的应力和变形分布，文献[3]建立了深沟球轴承的五自由度静力学模型，分析了滚动体的直径误差和数目、径向游隙、内外套圈滚道的圆度误差以及径向和轴向载荷对轴承载荷分布和非重复性跳动的影响，文献[4] 建立了轴承的静态力学模型，分析了单个滚子或多个圆柱滚子的直径过大时的载荷分布，文献[5]将滚子与内外圈的接触用非线性弹簧表示，运用虚功原理建立多组件系统的平衡方程，研究了单个或多个滚子存在直径误差时对载荷分布的影响，文献[6]用非线性弹簧等效滚子与滚道的接触作用建立力学模型，用Newton- Raphson法求解滚子上的接触载荷，在此基础上研究了滚子直径误差和套圈滚道几何形状误差对载荷分布的影响，文献[7]根据弹性接触理论建立了滚针轴承在内外圈倾斜时的力学模型，通过迭代求解得到不同工况下的载荷分布，文献[8]利用切片法分析了轴承的接触问题，并考虑了内外圈倾斜、轴承游隙等对轴承载荷分布的影响。

以上文献大多是采用建立力学模型，得到解析解的方式进行分析，本文旨在通过建立有限元模型进行详细分析，同时将影响轴承寿命的多种制造误差与装配误差纳入到轴承传动分析中，分析各类误差对载荷分布、应力分布等的影响。通过本文方法可以比较全面直观地得到轴承各部分的应力应变分布情况，快速找出轴承传动过程中的薄弱区域以及不同误差对轴承传动性能的影响程度。同时为滚动轴承考虑多种随机误差影响的可靠性优化设计提供有利指导。

1　有限元模型的建立及验证

1.1有限元模型建立

本文选取的某型号圆柱滚子轴承主要参数如表1所示。

该轴承的材料为GCr15SiMn，材料弹性模量为E=2.06e5 MPa，泊松比v=0.3。模型的示意图如图2所示，内圈承受沿Z轴正方向Fr=120 kN的径向力，为便于后续分析，设1号滚动体与Z轴夹角为0°，并按逆时针方向对12个滚子进行编号。

表1　轴承的主要参数

图2　轴承示意图　　　　图3　有限元模型

模型中外圈施加固支约束，限制外圈的全部自由度；内圈的边界条件为U1=0，U2=0；各滚子分别在质心建立局部直角坐标系，分别限制12个滚子相对轴承轴线的周向平移自由度和轴向平移自由度。

有限元模型如图3所示，在滚子与内外圈接触处进行网格细化，共划分63 648个C3D8R单元，79 334个节点。

1.2模型验证

求解后得轴承应力分布如图4所示，滚子下半部分的5个滚子与内外圈的接触处存在应力，其余滚子没有应力。1号滚子与内外圈接触处应力较大，往两侧对称减小，且滚子与内圈的应力均大于与外圈的应力。

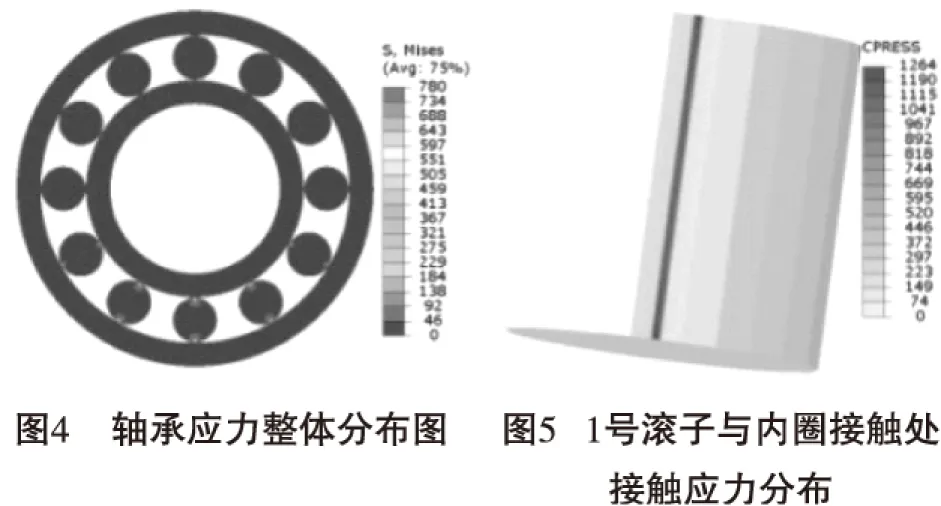
图5为轴承最底端1号滚子与内圈接触处的接触应力，可以看出，应力分布近似为狭长的矩形，且应力沿滚子轴向的分布并不均匀，端部出现了明显的应力集中。轴承最大接触应力出现在1号滚子端部与内圈接触处，为1 264 MPa。

下面利用赫兹接触理论计算接触应力[9]，最大接触应力σmax为：

式中：Q—滚子上的载荷(N)；b—接触半宽(mm)。

接触半宽b为：

式中：μ1，μ2—滚子和套圈的泊松比；E1，E2—滚子和套圈的弹性模量(MPa)；∑ρ—轴承的主曲率和(mm-1)。

计算得σmax=1 222MPa

由表2知通过有限元法计算的结果与赫兹理论计算的结果相差3.4%，说明建立的该有限元模型是可行的。

表2Hertz接触理论和有限元方法分析结果对比

Hertz理论有限元法误差轴承最大接触应力1222MPa1264MPa3.4%

2　无误差时的接触应力分析

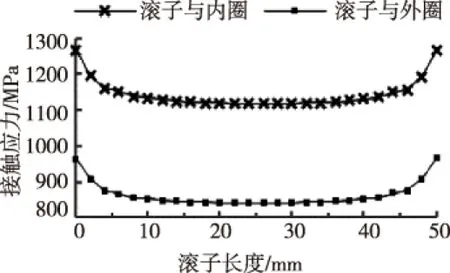
图6　1号滚子与内外圈　　　　沿轴向的接触应力

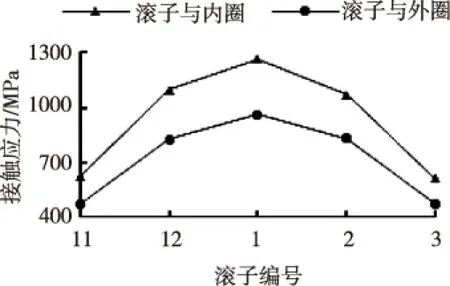
图7　各滚子与内外圈接触　　　区域最大接触应力

如图6所示为1号滚子与内外圈矩形接触区域中心处沿轴向的接触应力分布情况，从图中可以看出滚子与内圈的接触应力大于滚子与外圈的接触应力。两接触区域中部应力分布都比较均匀，两侧端部应力增加都较大，这种现象称之为“边缘效应”。

图7所示为各滚子与内外圈接触区域的最大接触应力，可以看出位于径向载荷作用线上的1号滚子接触应力最大，随着与径向载荷作用线夹角的增大，各滚子上的接触应力逐渐减小，且对称于该作用线。各滚子与内圈的接触应力均大于与外圈的接触应力。

3　制造误差对接触应力的影响

3.1游隙对应力的影响

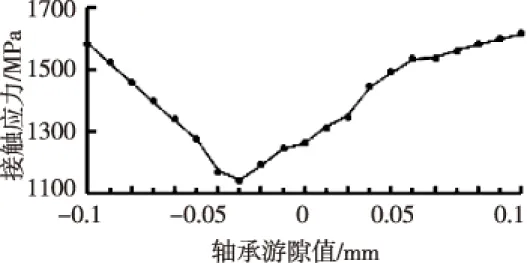
图8　安装游隙对轴承最大　　接触应力的影响

图8所示为游隙值由-0.10 mm至0.10 mm变化时轴承的最大接触应力变化情况，图9所示为游隙值由-0.05 mm至0.05 mm变化时各滚子与内圈接触处的最大接触应力。从中可以看出：

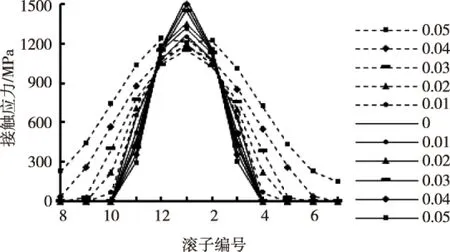
图9　不同游隙值时各滚子与内圈的最大接触应力

1)轴承安装游隙为正(即滚动体与内外圈间是间隙配合)时，随着游隙值的增大，轴承最大接触应力一直增大。原因是与径向载荷作用线夹角较小的1、2、12号滚子承受的载荷分量变大，使径向载荷更加集中地分布于少数滚子，引起最大接触应力的增大，当游隙值为0.05 mm时，增大21.5%，而与径向载荷作用线夹角较大的3、11号滚子承受的载荷分量变小，导致其上的接触应力减小。可以看出轴承游隙较大时将加剧载荷分布的不均性，并使最大接触应力值增大。

2)轴承安装游隙为负(即滚动体与内外圈间是过盈配合)时，随着负游隙的增大，受载滚子逐渐增多直至所有滚子均受载，而轴承最大接触应力则先减小后增大。第一个阶段，游隙从0 mm到-0.03 mm变化时，受载后轴承工作游隙为正值，受载滚子逐渐增多，径向载荷越来越均匀的分布在下半圈的5个滚子上，使整个轴承的最大接触应力逐渐减小，在游隙值为-0.03 mm附近时接触应力最小，为1 143 MPa，减小9.6%。第二个阶段：游隙超过-0.03 mm以后，受载后轴承工作游隙仍为负值，此时虽受载，但所有滚子均与内外圈接触，轴承最大接触应力逐渐增大，此时轴承内部的接触应力是径向载荷和过盈接触综合作用的结果。

3.2滚子直径误差对接触应力的影响

3.2.11号滚子存在直径误差

图10所示为1号滚子的直径存在不同误差值时轴承的最大接触应力。当1号滚子直径误差为正时，轴承内部最大接触应力随误差值的增大而增大；而当1号滚子直径误差为负值时，随着误差的增大，轴承内部最大接触应力先减小后增大，当误差值在-0.01 mm时达到最小值1 221 MPa，减小3.4%。

图11所示为1号滚子的直径存在不同误差值时各滚子与内圈接触处的最大接触应力。从中可以看出：

1)1号滚子直径误差为正时，只有1号滚子的接触应力逐渐增大，其余滚子的接触应力均逐渐减小，原因是1号滚子直径逐渐增大，其上的载荷分量也逐渐增大，导致该滚子上的接触应力越来越大，而其余滚子上的载荷分量则逐渐减小，导致其余滚子上接触应力逐渐减小。

2)1号滚子直径误差为负值时，比较承载的各滚子应力，发现1号滚子的接触应力一直减小，且下降趋势较为明显，其余滚子的接触应力则一直增大，原因是1号滚子直径减小，使得其上的载荷分量减小，使该滚子上的接触应力减小，而其余滚子上的载荷分量持续增大，导致其余滚子上接触应力增大。

3.2.22号、3号、4号滚子存在直径误差

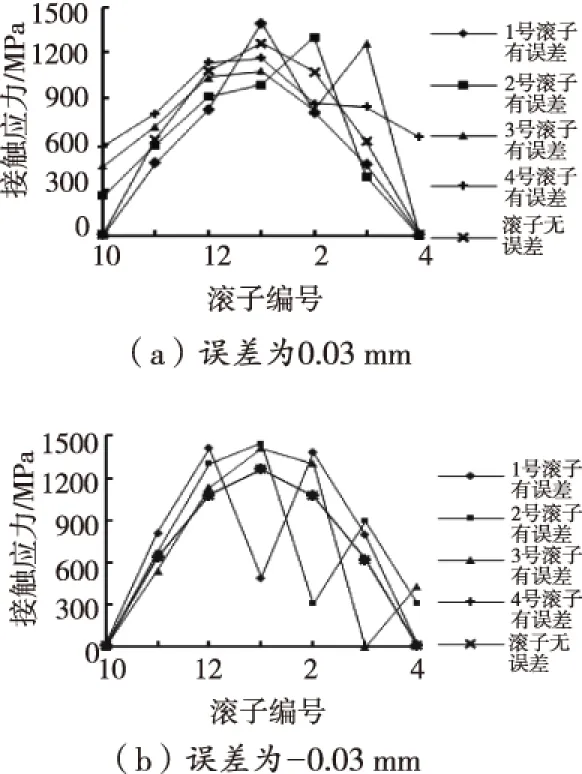
图12　2号、3号、4号滚子存在直径误差时各滚子与内圈的最大接触应力

本节分析了2号、3号、4号滚子分别存在直径误差时，轴承最大接触应力以及各滚子接触应力变化情况。图12为2号、3号、4号滚子存在直径误差时各滚子与内圈的最大接触应力变化情况。当某滚子直径误差值为正时，该滚子上的接触应力比无误差时要大，并使该滚子两侧附近的滚子上的接触应力减小；当1-3号滚子直径误差为负时，该滚子上的接触应力比无误差时要小，并使该滚子两侧附近的滚子上的接触应力增大，4号滚子直径误差为负时，所有滚子上接触应力无变化。

表3(a)是不同滚子存在正直径误差时各滚子上的接触应力变化情况。当1号滚子存在正误差时，只有1号一个滚子接触应力增大；2号滚子存在正误差时，2号和10号两个滚子接触应力增大；3号滚子存在正误差时，3号、10号和11号三个滚子接触应力增大；4号滚子存在正误差时，4号、10号、11号和12号四个滚子接触应力增大。可知存在误差的滚子越靠近两侧，会引起另一侧更多滚子上接触应力增大。

表3(b)是不同滚子存在负直径误差时各滚子上的接触应力变化情况。1号和2号滚子存在负的直径误差时，其余滚子接触应力均增大；3号滚子存在负的直径误差时，使另一侧的11号滚子接触应力也减小；4号滚子存在负的直径误差对接触应力无影响。

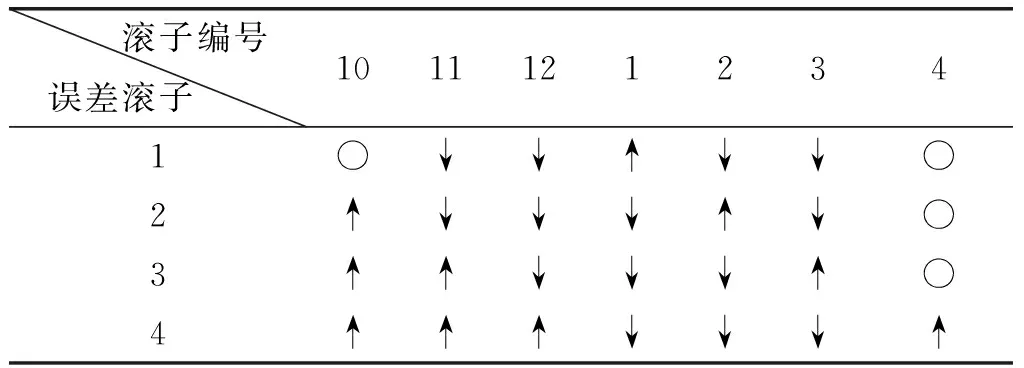
表3　1-4号滚子存在直径误差时各滚子上的接触应力变化情况　(a)误差值为0.03 mm

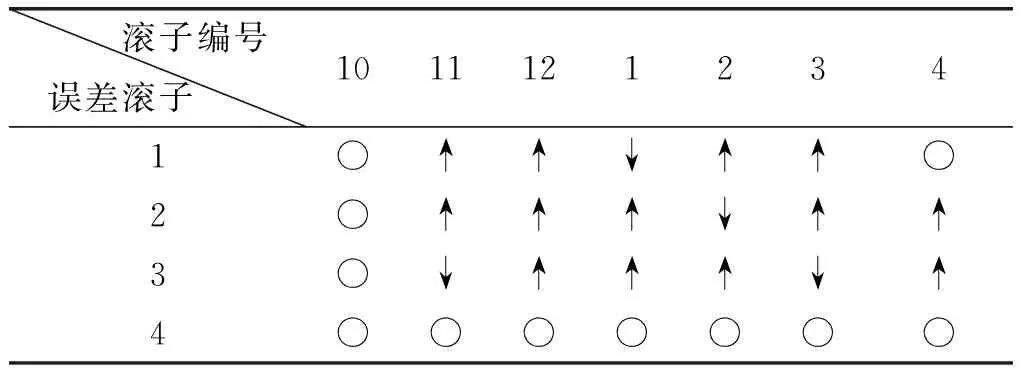
(b)误差值为-0.03 mm

注：○表示无变化，↑表示增大，↓表示减小

4　装配误差对接触应力的影响

4.1内圈相对外圈绕X轴偏转

图13为内圈相对外圈绕X轴偏转时(偏转角设为β)各滚子与内圈的最大接触应力，从图中可以看出各受力滚子上的最大接触应力都随偏转角β的增大而增大。内外圈的相对偏转会使各滚子与套圈的接触区域受力不均匀性加剧，使接触区域一侧应力增大，另一侧应力减小，图14以1号滚子与内圈沿轴向的接触应力为例。

4.2内圈相对外圈绕Z轴偏转

图15　内圈相对外圈绕Z轴偏转时　各滚子与内圈的最大接触应力

图15所示为内圈相对外圈绕Z轴偏转时(偏转角设为γ)各滚子与内圈的最大接触应力，除1号滚子外其余各滚子与套圈的接触区域受力不均匀性加剧，使接触区域一侧应力增大，另一侧应力减小。1号滚子上的最大接触应力基本保持不变，其余各受力滚子上的最大接触应力都随偏转角γ的增大而增大。

4.3不同偏转方式的对比

图16表示不同偏转角对轴承最大接触应力的影响，从图16可以看出：

1)当偏转角β从0°到0.008°时，轴承的最大接触应力从1 264 MPa变为1 511 MPa, 增大了19.5%，在此范围斜率为30 857 MPa/deg(MPa/deg表示偏转角变化1°时接触应力的变化量)。

2)当偏转角γ从0°到0.01°时，最大接触应力基本不变，但从0.01°到0.03°时，最大接触应力从1 267 MPa变为1 498 MPa, 增大了18.2%，此范围内的斜率为11 550 MPa/deg。

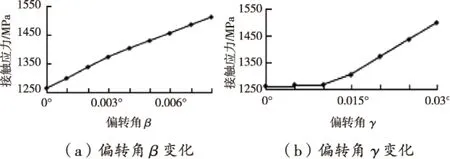
图16　不同偏转角对轴承最大接触应力的影响

由此可以看出，当径向载荷沿Z轴时，偏转角β比偏转角γ对接触应力影响更大。

5　结论

1)无误差时，滚子端部存在边缘效应，滚子与内圈的接触应力均大于滚子与外圈的接触应力。

2)轴承游隙过大或过小都会使轴承接触应力异常增大，在小负游隙时接触应力较小。

3)单个滚子的直径存在正误差时该滚子上接触应力变大，而邻近滚子上接触应力减小，负误差时该滚子上接触应力变小，而邻近滚子上接触应力增大，应尽量避免1号滚子的直径出现正误差。

4)内外圈相对偏转时会使滚子一侧接触应力变大，另一侧接触应力变小；绕X轴的偏转角β比绕Z轴的偏转角γ对轴承接触应力的影响大。故装配时应控制偏转角的范围，特别是偏转角β。

[1]陈龙，杜宏武，武建柯，王玲. 风力发电机用轴承简述[J].轴承， 2008(12)：45-50.

[2]Demirhan N, Kanber B. Stress and displacement distributions on cylindrical roller bearing rings using FEM[J]. Mechanics Based Design of Structures and Machines,2008, 36(1): 86-102.

[3]李传顺. 深沟球轴承元件几何误差对轴承性能的影响[D].大连理工大学,2013.

[4]Chen G C, Mao F H, Wang B K. Effects of off-sized cylindrical rollers on the static load distribution in a cylinder roller bearing[J]. Journal of Engineering Tribology, 2012, 226(8): 687-696.

[5]Yu S D, Wang D L, Dong H M, et al. A new method for determining load distributions among rollers of bearing with manufacturing errors[J]. Journal of Mechanical Engineering Science, 2013, 227(11): 2402-2415.

[6]王宝坤，毛范海，孙守林，王德伦. 圆柱滚子轴承零件几何误差对载荷分布的影响[J].轴承，2014(2)：30-35.

[7]白晓波，吉晓民，郭磊. 内外圈轴线相对倾斜时的滚针轴承载荷分布研究[J].机械强度,2014(2)：216-221.

[8]燕晓慧，李继庆，袁茹. 内外圈相对倾斜对圆柱滚子轴承承载能力的影响分析[J].机械科学与技术,1996, 15(1): 101-104.

[9]Harris T A. Rolling bearing analysis[M].New York: Wiley, 1984.

Effects of manufacture and assembly errors on contact stress on the cylindrical roller bearing

WANG Qiuzhi, JIANG Wei, LIU Huahan

We established the static finite element model of a cylindrical roller bearing under 120 kN radial force in ABAQUS, and verified the model by Hertz elastic contact theory. With finite element method, we analyzed the distribution of contact stress on the bearing under error-free conditions, then we analyzed the distribution of contact stress and the change of the maximum contact stress when there were clearance, roller diameter error or relative deflection of inner ring and outer ring. The results showed that the contact stress was relatively low when there were small negative clearance, that the contact stress would increase when the roller diameter was too large or too small, and that different deflection conditions of inner ring and outer ring had different effects on the contact stress. This study can provide guidelines for the improvement of the quality and service performance of the bearing.

cylindrical roller bearing，contact stress，clearance，roller diameter，deflection

TH133.33

A

1002-6886(2016)04-0032-06

王秋志(1990-)，男，硕士研究生，主要研究方向：有限元仿真及结构优化。

2015-12-25