考虑轴头驱动和侧倾力矩的轮胎接地性态建模

汪　晨　黄海波　刘金朋　李洪宇

宁波大学，宁波，315211



考虑轴头驱动和侧倾力矩的轮胎接地性态建模

汪晨黄海波刘金朋李洪宇

宁波大学，宁波，315211

采用欧拉梁和侧向分片的方法模拟轮胎侧向变形特性，利用二元傅里叶级数构造带束层单元的位移场，胎面横截面外轮廓设定为二次函数，建立了基于驱动力矩和侧倾力矩的轮胎三维接地性态解析计算模型。结合轮胎刷子模型计算了轮胎的纵向力和侧向力，并进行了验证。结果表明，模型具有较高的精度和效率。研究结果可为研究轮胎磨损和轮胎力学特性提供更为精确的三维接地压力分布解析模型，并为轮胎物理模型的解析研究提供新的思路和方法。

轮胎；弹性薄壁模型；接地性态；欧拉梁；侧向分片

0　引言

接地界面是轮胎与地面的唯一接触界面，其力学特性是影响轮胎磨损和车辆操稳性、平顺性的重要因素。轮胎接地界面性态包括接地压力及其分布、接地印迹形态等因素。由于数据的特殊性，接地界面性态较难获得连续的动态时域数据，但是可以利用现代测试技术较为容易地采集轮胎与车辆连接处的轴头力[1]。因此，通过轴头力预测轮胎接地界面特性对研究轮胎力学特性具有十分重要的意义。

鉴于接地性态的重要性，很多学者采用有限元方法[2-3]、理论解析方法[4-5]和试验方法[6-7]对轮胎滚动过程中的接地性态进行了建模、验证和预测。为了实现直接由轮胎的结构、材料参数预测轮胎的接地性态和瞬态特性，获得各变量、参数间的内在联系，理论解析法大量应用到轮胎接地性态的模拟中。国内外学者最早假设接地压力均匀分布或抛物线分布，使用刷子模型计算轮胎六分力，分析轮胎的侧偏、回正等现象[8]。在现代动力学模型中，Guo等[9]提出的UniTire模型使用了拟合的接地压力经验公式；由环模型发展而来的SWIFT模型[10]需要包容模型来提供等效路形以处理轮胎-地面接触问题；FTire模型[11]则由有限元模型来提供计算时需要的接地压力数据。同时，接地界面性态是描述轮胎接地面力学行为特性的重要指标，可以描述轮胎与路面间作用力及其分布等指标的关键信息，而轮胎磨损发生在轮胎的接地界面内[12-13]，故接地界面性态也是决定轮胎磨损量及胎面磨损形态的重要因素。因此，轮胎接地界面性态模型对发展轮胎动力学及轮胎磨损预测模型至关重要[14-15]。

驱动力矩和侧倾力矩是轴头六分力中两个非常重要的力矩，对车辆稳态运动、转向以及轮胎定位参数的合理选择都有重要影响[16]。鉴于这一重要性，本文建立了一种基于轴头驱动力矩和侧倾力矩的轮胎三维接地性态解析预测模型，该模型考虑了轮胎沿侧向弹性变形的影响，可以给出轮胎接地界面的三维压力分布和接地印迹形态；分析了驱动力矩和侧倾力矩对轮胎接地压力分布的影响规律。

1　轮胎计算模型

1.1建模思路

本文利用梁模型对二维轮胎模型进行侧向扩展来构建三维轮胎物理模型，运用哈密尔顿原理和拉格朗日方程，建立了驱动力矩和侧倾力矩共同作用下的轮胎运动微分方程；借助二元傅里叶级数构造带束层位移函数对高阶微分方程进行降阶，结合驱动力矩和侧倾力矩的初始条件求解轮胎接地压力分布。模型的输入和输出关系如图1所示。

图 1　模型输入与输出的关系

1.2弹性薄壁模型

图 2　轮胎弹性薄壁模型

如图2所示，轮胎简化为四部分：轮毂、胎侧、带束层和胎面。模型中视轮毂为刚体，轴头力均施加于轮毂中心，带束层简化为弹性薄壁圆筒。轮毂与带束层之间均匀分布着三个方向的弹簧和阻尼，表示气压与胎侧材料产生的黏弹性。带束层外侧连接代表胎面弹性的径向弹簧。另外，模型胎面外轮廓参照轮胎真实形貌，设为曲率较小的二次函数，一方面更接近于实际，另一方面也可以使微分方程组变为非齐次线性方程组，利于方程求解并提高解算速度。

如图3所示，由于带束层侧向的曲率半径比周向半径大得多，故假定带束层侧向曲率半径为无穷大，视为放置于黏弹性基上的欧拉梁。该建模方法与Gim等[17]提出的方法类似，区别在于后者侧重于研究轮胎接地压力沿侧向的分布规律，没有系统地考虑到轮胎纵向和侧向弹性变形的联系。

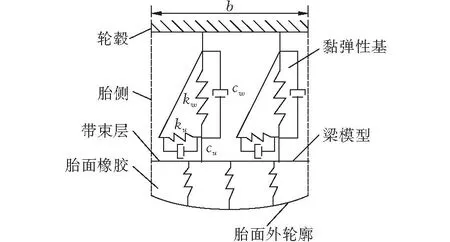
图 3　有黏弹性基的梁模型

1.3轮胎运动微分方程

如图2所示，本文建立了直角坐标系xyz和x*yz*，分别用于描述固定坐标系和旋转坐标系下的驱动力矩和侧倾力矩。为辅助模型分析与计算，另建立了相互耦合的旋转柱坐标系rθy和固定柱坐标系rφy描述带束层单元的空间坐标。旋转坐标系与轮胎保持相对静止，在该坐标系下分析轮胎运动可以忽略轮胎的转动，便于建立运动微分方程，但在解算后期为方便表达轮胎接地性态，需将方程转换至固定坐标系。

由于轮胎结构的复杂性，直接对带束层单元进行受力分析，建立完整的轮胎振动方程有一定难度，故本文从能量的角度建模并考虑到轮胎侧向扩展，改进了文献[18]中的相关方程，建立拉格朗日方程如下：

(1)

(2)

(3)

(4)

(5)

式中，L为拉格朗日函数；“·”代表对时间求偏导；θ为带束层单元在旋转坐标系内的角度坐标；“′”代表对θ求偏导；w、v、u、θr、γM为轮胎振动系统的广义坐标(广义坐标是用于描述带束层单元的空间位移量)，其中，w、v、u分别为带束层单元沿轮胎径向、切向、侧向的位移量，θr、γM分别为考虑轮胎转动角度与侧倾角的波动；Q1、Q2、Q3分别为三个方向的路面激励; Q4、Q5分别为驱动力矩和侧倾力矩。

基于拉格朗日方程得到的轮胎多自由度连续系统运动微分方程组为

(6)

1.4驱动力矩的振动方程

(7)

Tθ=-2πbkvR3θr

(8)

(9)

1.5侧倾力矩的振动方程

(10)

Mr=-πR3bkuγM

(11)

(12)

1.6轮胎运动方程求解

假设带束层单元侧向位移u与切向位移v成线性关系，根据高拉伸刚度的子午线轮胎周向不可扩展假设，可以得到w、v、u之间的关系：

(13)

u=ηv

(14)

式中，η为侧向位移u与切向位移v的相关系数。

由于式(6)为高阶偏微分方程，为求解方程，本文结合二元傅里叶级数与待定系数法构造带束层切向位移函数,借此对高阶方程进行降阶。设

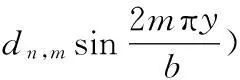
(15)

式中，an,m、bn,m、cn,m、dn,m为系数。

将式(13)～式(15)代入式(6)并转换至固定坐标系下，得到以下线性方程组：

(16)

(17)

m11=ρh(n2+1+η)

g12=2nΩρh(n2-1)

1.7初始条件

轮胎做稳态运动时，变量θr、γM恒为0。将式(14)、式(15)代入式(7)、式(10)中，求解可得系数a0,0和a1,0，具体计算公式如下：

(18)

(19)

1.8轮胎接地压力分布

由式(16)、式(17)可见，求解线性方程组须代入地面作用反力qw、qv、qu，本文利用胎面橡胶变形量建立地面作用反力函数从而对方程组进行求解。由于带束层外侧仅连接了胎面径向弹簧，本模型仅考虑沿轮胎径向的地面反力qw，故qv和qu恒为0。如图4所示，轮胎受载后的总变形量为带束层径向位移w(φ,y)与胎面橡胶径向弹性变形量κ(φ,y)之和，故轮胎受到地面作用时的径向力qw(φ,y)为

qw(φ,y)=k1κ(φ,y)

(20)

(21)

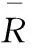
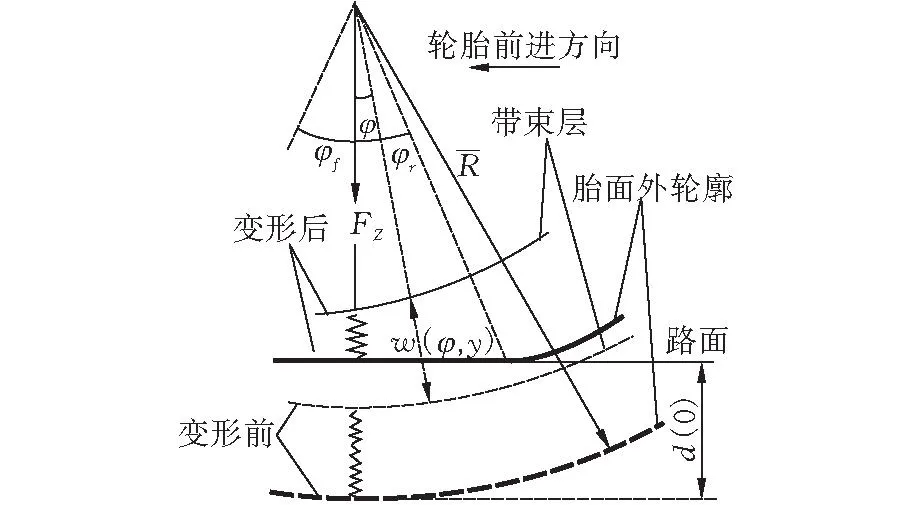
图 4　胎冠中心带束层变形几何图

求解φf(y)和φr(y)时，需对轮胎沿y轴进行分片处理，即将轮胎分为n片较窄圆环。第i片内圆环的接地前角φf和后角φr不随y坐标变化，通过计算机程序的反复迭代求得误差范围内的近似解。

图5所示为侧倾轮胎的变形示意图，侧倾角γ的正负符号仅代表轮胎倾斜方向，本文取沿轮胎滚动方向看轮胎顶部相对于接地印迹中心向右侧移动为正，反之为负。由图5可知，下沉量d(y)与侧倾角γ的关系为

(22)

式中，d0为胎冠中心处轮胎下沉量。

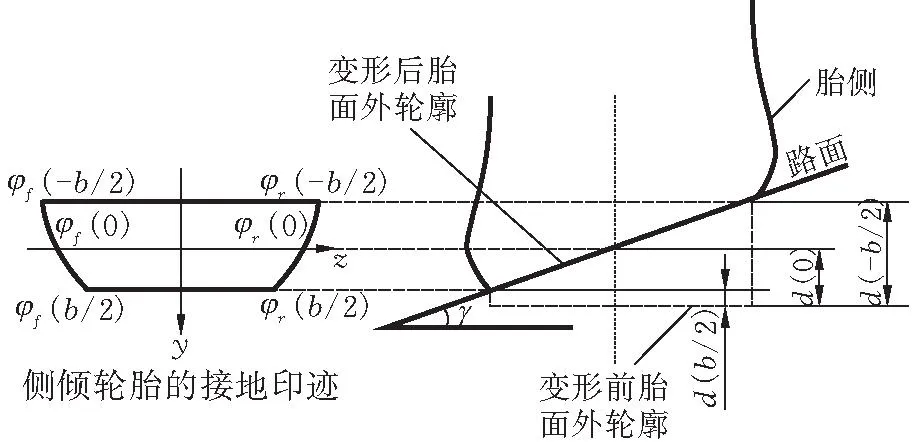
图 5　侧倾轮胎变形图

将式(20)代入线性方程组式(16)、式(17)中，解得系数an,m、bn,m、cn,m、dn,m，重新代回式(20)中通过反复迭代满足边界条件，即接地印迹边界处接地压力为0，从而将φf和φr收敛至误差范围内，得到地面的径向作用反力qw(φ,y)，解得轮胎接地界面垂直压力分布函数qz(φ,y)，接地印迹内任意点的接地压力qz(φ,y)为

qz(φ,y)=qwcosφcosγ

(23)

2　侧倾力矩和驱动力矩对轮胎接地压力分布的影响

本文计算了侧倾力矩分别为0、15 N·m、30 N·m时以及驱动力矩分别为0、15 N·m、30 N·m时的接地压力分布，并讨论了侧倾力矩和驱动力矩对接地印迹形状和接地应力分布的影响规律。各工况的计算时间在280～310 s之间。

2.1侧倾力矩对接地压力分布的影响

初始工况如下：垂向载荷为4 kN，对应的胎冠中心处下沉量为0.02 m，驱动力矩为30 N·m。计算结果如图6～图11所示，侧倾力矩为0时，轮胎接地印迹大致呈矩形。随着侧倾力矩的增大，接地印迹逐渐呈现为梯形，且梯形两腰为曲线分布，斜率逐渐增大，该现象与诸多有限元分析结果[19]一致。

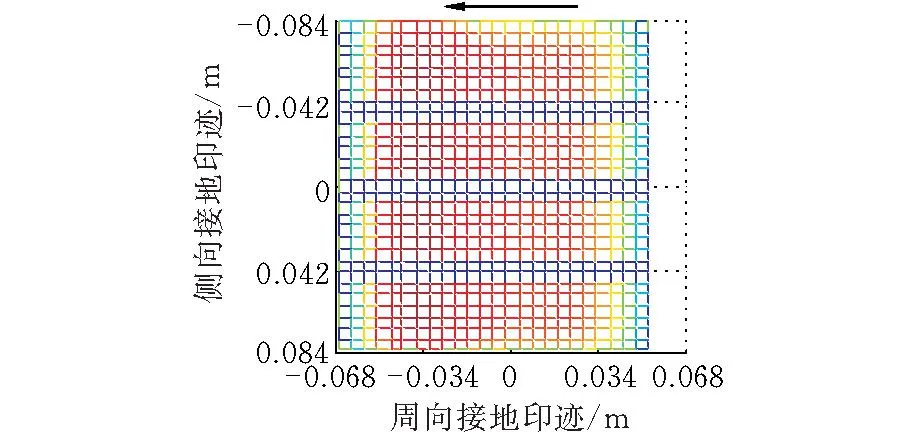
图 6　接地印迹(M=0)

图 7　接地印迹(M=15 N·m)

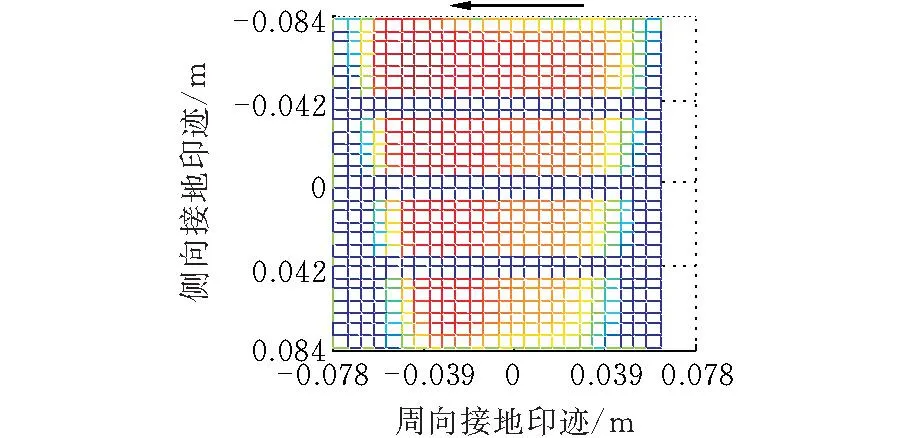
图 8　接地印迹(M=30 N·m)

图 9　接地压力分布(M=0)

图 10　接地压力分布(M=15 N·m)

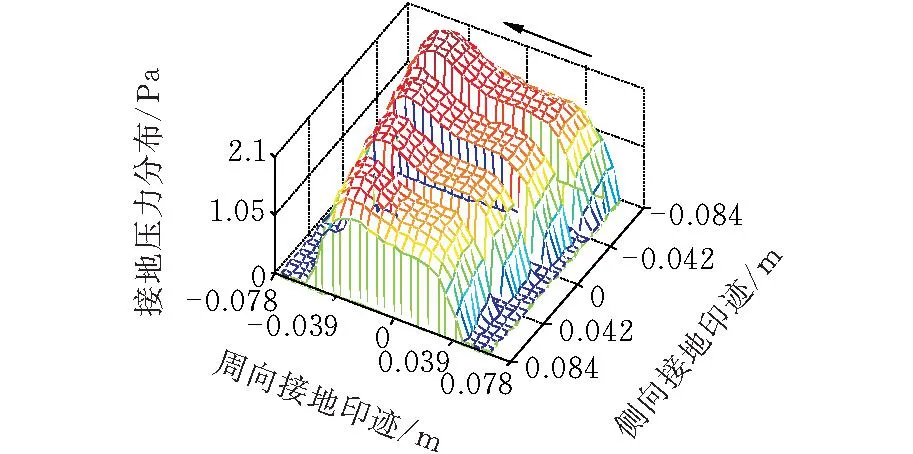
图 11　接地压力分布(M=30 N·m)

2.2驱动力矩对接地压力分布的影响

初始工况如下：垂向载荷为4 kN，对应的胎冠中心处下沉量为0.02 m，侧倾力矩为30 N·m，轮胎接地压力的计算结果如图12～图17所示，驱动力矩由0增加至30 N·m，轮胎接地印迹前部的长度由0.07 m伸长为0.078 m，后部由0.07 m缩短为0.059 m，接地压力分布的纵向不对称性更加明显。这是因为驱动力矩的增大会引起轮胎转速提高,离心力和弹性变形增大，轮胎材料的变形迟滞导致高压力区向轮胎前进方向移动。这与文献[20]的研究结果一致。

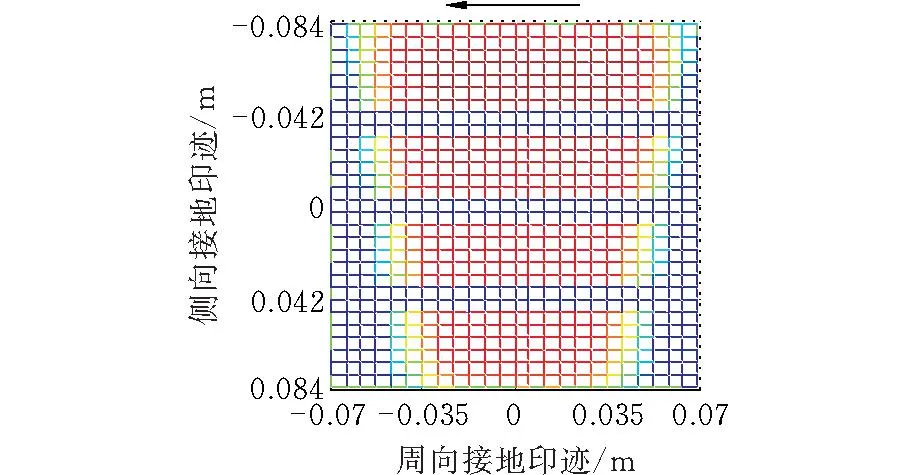
图 12　接地印迹(T=0)

图 13　接地印迹(T=15 N·m)

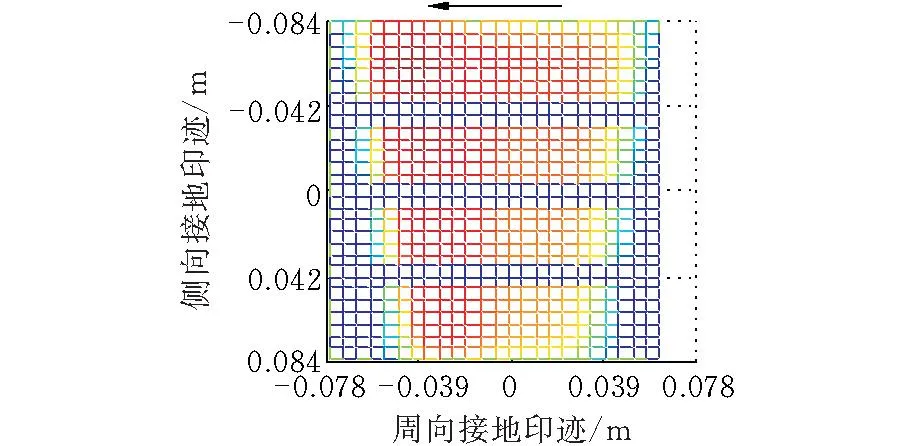
图 14　接地印迹(T=30 N·m)

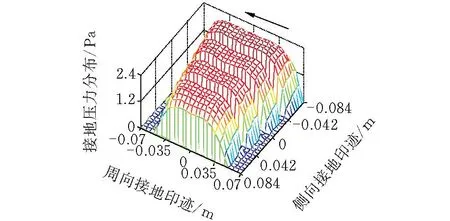
图 15　接地压力分布(T=0)

图 16　接地压力分布(T=15 N·m)

图 17　接地压力分布(T=30 N·m)

3　结果验证和讨论

利用本文模型的计算结果，结合刷子模型计算了轮胎的纵向力、侧向力，并与Kim等[21]的计算和实验结果进行对比。轮胎初始工况如下：垂向载荷为4.5 kN，对应的胎冠中心处下沉量为0.0204 m，轮胎运动速度为100 km/h，计算结果如图18、图19所示。比较后发现，当滑移率小于0.25时，本文纵向力、侧向力的相对误差绝对值总体上更接近于实验结果并小于文献[21]的计算误差，尤其此时侧向力相对误差的最大值仅为3.25%，远小于文献[21]的误差最大值10.04%。这说明小滑移率下本文的计算结果比文献[21]的计算结果更贴近实验结果。当滑移率大于0.25时，本文纵向力、侧向力的相对误差会略大于文献[21]的计算误差，但与实验结果偏差不大，分别不超过5.6%和4.7%。因此，本文构建的轮胎三维接地压力模型计算得出的二维接地压力分布具有较高的精度，能够较为准确地预测轮胎的纵向力、侧向力，且小滑移率时的计算精度更好。

图 18　纵向力曲线

图 19　侧向力曲线

4　结论

(1)结合欧拉梁、侧向分片的方法和接地印迹边界条件，可以实现侧倾力矩下轮胎轴向的压力分配。

(2)考虑轮胎切向和侧向弹性变形时，运用二元傅里叶级数来构造带束层单元的位移函数，对连续系统运动微分方程组进行降阶和简化，可以方便方程求解。

(3)将胎面轴向截面轮廓设定为二次函数，可以使运动微分方程组变为非齐次线性方程组，利于方程求解并提高解算速度。

(4)本文用轴头力预测轮胎三维接地压力分布，实现了轴头“点”力学特性到轮胎接地界面“面”力学特性的计算。模型的计算时间短，具有较好的精度，可用于轮胎动力学模型和轮胎磨损模型进行轮胎动力学特性和磨损的预测和解析计算。

[1]靳畅，周鋐，慕乐.基于频响函数法的路面激励下车轮轴头力的估计[J].汽车工程，2014, 36(4): 469-474.

Jin Chang, Zhou Hong, Mu Le. Estimation of Wheel Spindle Loads under Road Excitation Based on Frequency Response Function Method[J]. Automotive Engineering,2014, 36(4): 469-474.

[2]邱恩超，郭孔辉.基于环模型的轮胎有限元建模与仿真研究[J].汽车技术，2009(7):4-8.

Qiu Enchao, Guo Konghui. Tire FE Modeling Based on Circle Model and Simulation Study[J]. Automobile Technology, 2009(7): 4-8.

[3]Ghoreishy M H R. Finite Element Modeling of the Steady Rolling of a Radial Tyre with Detailed Tread Pattern[J]. Iranian Polymer Journal, 2009, 18(8):641-650.

[4]Kim S J, Savkoor A R.Contact Problem of In-plane Rolling of Tires on a Flat Road[J].International Journal of Vehicle Mechanics and Mobility,1997, 27(S1): 189-206.

[5]Wei Yintao, Fan Chengjian, Guan Dihua.Ring Model for Pneumatic Tires[J].Tsinghua Science and Technology, 2002,7(5): 496-501.

[6]Anghelache G,Moisescu R,Sorohan S, et al.Measuring System for Investigation of Tri-axial Stress Distribution across the Tyre-road Contact Patch[J]. Measurement, 2011, 44(3): 559-568.

[7]Mohsenimanesh A, Ward S M. Estimation of a Three-dimensional Tyre Footprint Using Dynamic Soil-tyre Contact Pressures[J]. Journal of Terramechanics, 2010, 47(6): 415-421.

[8]Gäfvert M, Svendenius J.Construction of Novel Semi-empirical Tire Models for Combined Braking and Cornering[R]. Lund:Departement of Automatic Control,Lund Institute of Technology, 2003.

[9]Guo K, Lu D, Chen S, et al. The UniTire Model: A Nonlinear and Non-steady State Tyre Model for Vehicle Dynamics Simulation[J].Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 2005, 43(S1): 341-358.

[10]Schmeitz A J C, Besselink T J M, Jansen S T H.TNO MF-SWIFT[J]. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 2007, 45(S1): 121-137.

[11]Gipser M. Flexible Ring Tire Model Documentation and User’s Guide[EB/OL]. (2013-03-01).http://www.ftire.com.

[12]董保利，左曙光，吴旭东.轮胎均匀磨损建模与仿真[J].计算机仿真，2009(2):274-277.

Dong Baoli，Zuo Shuguang，Wu Xudong.Modeling and Simulation of Even Tire Wear[J].Computer Simulation，2009(2): 274-277.

[13]王吉忠，庄继德，李日春.轮胎胎面橡胶块与刚性路面摩擦接触数值分析[J].农业工程学报，1998,14(2) :104-108.

Wang Jizhong，Zhuang Jide，Li Richun. Analysis of Tire Tread Rubber Friction and Rigid Pavement Contact Numerical [J].Transactions of the CSAE,1998,14(2) :104-108.

[14]Huang Haibo, Chiu Yijui, Wang Chen, et al.Three-dimensional Global Pattern Prediction for Tyre Tread Wear[J]. Proceedings of the Institution of Mechanical Engineers Part D-Journal of Automobile Engineering, 2014,229(2):197-213.

[15]候臣元. 轿车轮胎磨损有限元仿真与分析[D].上海：同济大学, 2011.

[16]郭孔辉，杨杰.大侧倾角下UniTire稳态侧倾侧偏工况侧向力模型[J].机械工程学报，2014，50(8): 95-101.

Guo Konghui,Yang Jie.Steady-state UniTire Lateral Force Model under Sideslip Combined with Large Camber Condition[J]. Journal of Mechanical Engineering，2014，50(8): 95-101.

[17]Gim G, Nikravesh P. A Three Dimensional Tire Model for Steady-state Simulations of Vehicles[J]. SAE Technical Paper 931913, 1993.

[18]Gong S. A Study of In-plane Dynamics of Tires[D]. Delft:Delft University of Technology, 1993.

[19]Cheng Gang, Wang Weidong, Zhao Guoqun, et al. Influence of Camber Angle on Rolling Radial Tire under Braking State[J]. Procedia Engineering 2011,15(1): 4310-4315.

[20]路永婕，杨绍普，李韶华.载重子午线轮胎与路面相互作用的分析[J].公路交通科技，2009,26(12): 12-16.

Lu Yongjie, Yang Shaopu, Li Shaohua. Analysis of Interaction between Truck Radial-ply Tire of Heavy Duty Vehicle and Road Surface[J]. Journal of Highway and Transportation Research and Development,2009,26(12): 12-16.

[21]Kim S, Nikravesh P E, Gim G. A Two-dimensional Tire Model on Uneven Roads for Vehicle Dynamic Simulation[J].Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 2008, 46(10):913-930.

(编辑陈勇)

A Tire Model for Contact Ground State Considering Driving and Overturning Torques at Axle Head

Wang ChenHuang HaiboLiu JinpengLi Hongyu

Ningbo University，Ningbo，Zhejiang，315211

The lateral deformation was considered utilizing Euler beam and divided tire into slices in lateral direction. The displacements of belt elements were computed with two-variables Fourier series. The profile of tire cross-section was described as quadratic function. The model was verified by comparing longitudinal and lateral forces with tests. The results show that the model is more precision and efficiency. The methodology for building tire 3D contact model can be provided to explore the tire wear and mechanics behaviors.

tire; thin elastic ring model; contact ground state; Euler beam; lateral slice

2015-04-08

国家自然科学基金资助项目(51205213)

U463.341DOI：10.3969/j.issn.1004-132X.2016.07.021

汪晨，男，1991年生。宁波大学机械工程与力学学院硕士研究生。主要研究方向为滚动体摩擦磨损。黄海波(通信作者)，男，1978年生。宁波大学机械工程与力学学院副教授。刘金朋，男，1993年生。宁波大学机械与力学学院硕士研究生。李洪宇，男，1990年生。宁波大学机械工程与力学学院硕士研究生。