一种消防六足机器人及其腿部机构运动学分析

金振林　 张金柱　高　峰

1.燕山大学,秦皇岛,0660042.上海交通大学机械系统与振动国家重点实验室,上海,200240



一种消防六足机器人及其腿部机构运动学分析

金振林1,2张金柱1高峰2

1.燕山大学,秦皇岛,0660042.上海交通大学机械系统与振动国家重点实验室,上海,200240

提出了一种六足并联消防机器人，并进行了整机概念设计；经过对2UPS+UP机构进行变异,提出了一种新型三自由度易防护腿部机构；对该腿部机构进行了运动学分析，推导了位置反解方程和速度映射关系，分析了工作空间，绘制了工作空间三维图，揭示了其驱动机构几何参数对该机器人越障能力和行走速度的影响规律，设计了一组合理的几何参数。所提出的六足机器人防护性好，在消防、核电泄漏及地震等救灾场合有很好的应用前景。

三自由度；六足机器人；运动学；工作空间

0　引言

从20世纪60年代开始，多足机器人就成为学者们争相研究的重要课题[1-2],然而用于消防、核电等恶劣环境下的多足机器人至今鲜有报道。据中国国家安监总局统计，大部分火灾发生现场地势狭窄、地形复杂、环境恶劣使得传统的消防及救援车难以到达和通过[3]。在核电消防领域，由于辐射和易燃易爆等环境特点,工作人员的生命安全受到了极大的威胁,多足消防机器人在这方面具有得天独厚的优势,但由于应用环境特殊，故对机器人的防护也有更加严格的要求。在消防及核电领域，美国、德国、法国、日本等发达国家取得了长足的进步[4-5],最具代表的是德国研制的OLE机器人[6]、美国研制的FFR-1[7-8]和Warrior机器人[9]。然而,这些机器人有的为了实现结构紧凑易防护目的而导致机体或腿部脆弱单薄，有的为实现大承载而体积庞大,这大大地限制了其在消防及核电领域的应用范围。2012年日本福岛核电站爆炸事故和2015年哈尔滨火灾事故表明，现有机器人在消防及核电方面的实际应用效果不佳。并联结构腿作为多足机器人腿的一种，具有承载能力强、驱动电机靠近基座或可在基座上等特点，使得其可防护性较高。上海交通大学高峰团队在2013年上海工业博览会展出的“章鱼机器人”采用并联结构腿，该机器人承载能力强、刚度大，但其电机随腿部实时地运动，很难进行腿部防护。

腿部设计作为多足机器人设计的关键环节,其设计的好坏直接关系到机器人的性能。本文根据多足生物的腿部运动特点和机器人防护要求，对2UPS+UP机构进行变异,提出了满足运动及防护要求的三自由度2RUS+RU+FD腿部机构(其中FD表示平行四边形放大机构,起到放大工作空间的作用),并基于该机构设计了一种并联六足机器人，推导了该机器人腿部机构的反解方程和速度映射关系，分析了工作空间，给出了一组较优的结构参数。

1　六足机器人整机概念设计与腿部机构介绍

1.1六足机器人整机概念设计

根据对六足动物整体布局[10]的研究,提出了并联六足机器人3-3面对称布局结构,如图1所示,在机架1上对称布置六条结构相同的机械腿3～8。在该布局形式下，上述六条腿自身所处运动平面平行或对称，能够使机器人控制系统简单，控制策略易于实施。此外，机架上还设有轴孔，以便于电机动力通过驱动轴9传到机器人腿部。机器人的腿部与地面的接触形式采用点接触的形式，从而可提高其对地面的适应能力。电气单元2整体布置于密闭机箱内，主要包括通信控制模块、传感器、主控制模块等。

1.机架　2.电气单元　3～8.机械腿　9.驱动轴图1　六足机器人结构示意图

综上所述,该机器人的电机部分和控制系统布置在密闭的机体内部,便于集中防护;裸露在外的机械腿为金属或特殊材料制备元件，对外部环境具有极高的适应性,从而使该机器人能够满足在消防、核电等恶劣环境下的消防特种作业要求。

1.2腿部机构介绍

1.2.1腿部机构构型介绍

地球上所有动物的行走过程本质上是动物足端实现的空间三维移动。对多足动物腿部自由度的分析表明,2转1移为最常见腿部自由度组合。文献[11]对常见2转1移机构优缺点进行了对比分析，结果表明2UPS+UP机构适合作为多足动物腿部机构。为了满足腿部电机及控制系统的防护要求，最大限度地减少驱动器或电机与机架的相对运动，本文根据约束螺旋综合法[12]对2UPS+UP机构进行运动副顺序重构，将上述机构演变为2PUS+PU机构。由于腿部的主要运动(前进、后退、下蹲、起立)及腿部在载重和快速奔跑时的主要承载力都分布在腿部的矢状面，腿部冠状面的运动主要为平衡、转弯、受冲击时的左右移动[13]，因此，结合螺旋理论使机构满足确定运动条件，将2PUS+PU机构的移动副竖直布置，获得含有一条主运动支链PU和两条对称布置的辅运动支链PUS的三自由度并联机构，再将该2PUS+PU机构作为腿部机构的驱动机构。为了降低机器人的高度和满足防护要求，利用杠杆传动将直线移动副转化为转动副，由此获得2RUS+RU机构，经过平行四边形放大机构FD，最终使腿部足端实现3个方向的移动，腿部机构简图如图2所示。

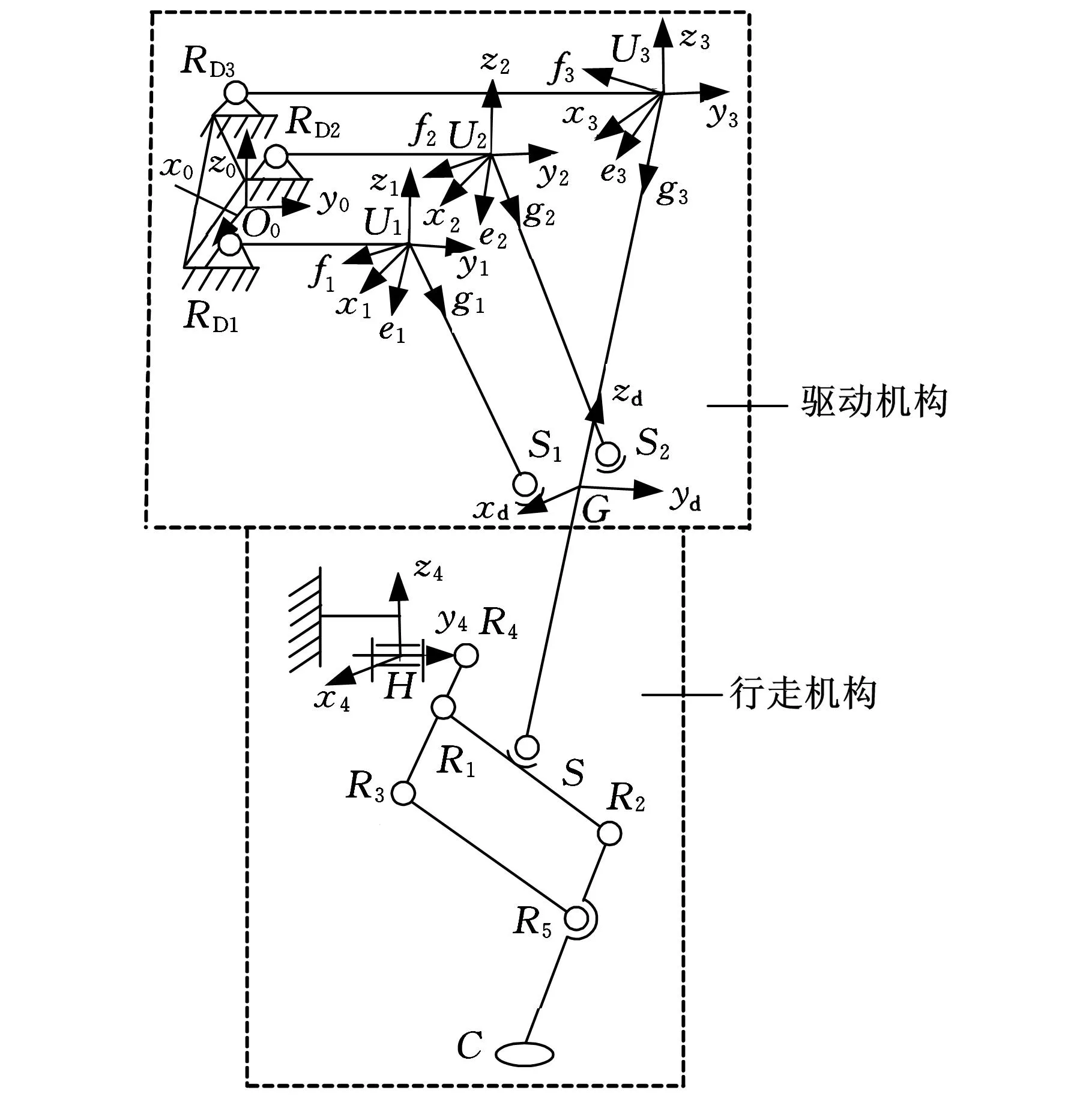
图2　腿部机构简图

1.2.2腿部机构组成及各部分连接方式

图3所示的机械腿由驱动机构和行走机构组成，其中驱动机构由一条主驱动支链和两条结构完全相同且关于主驱动支链所在的平面对称分布的辅驱动支链组成，其中主、辅支链分别通过电机33和3驱动，三个电机布置在竖直平面内的三角形的三个顶点上，其中两个辅驱动电机分别布置于三角形底边的两个顶点上，主驱动电机布置于三角形的另一顶点上；行走机构为被动机构,由FD机构组成，通过并联驱动机构驱动其运动。

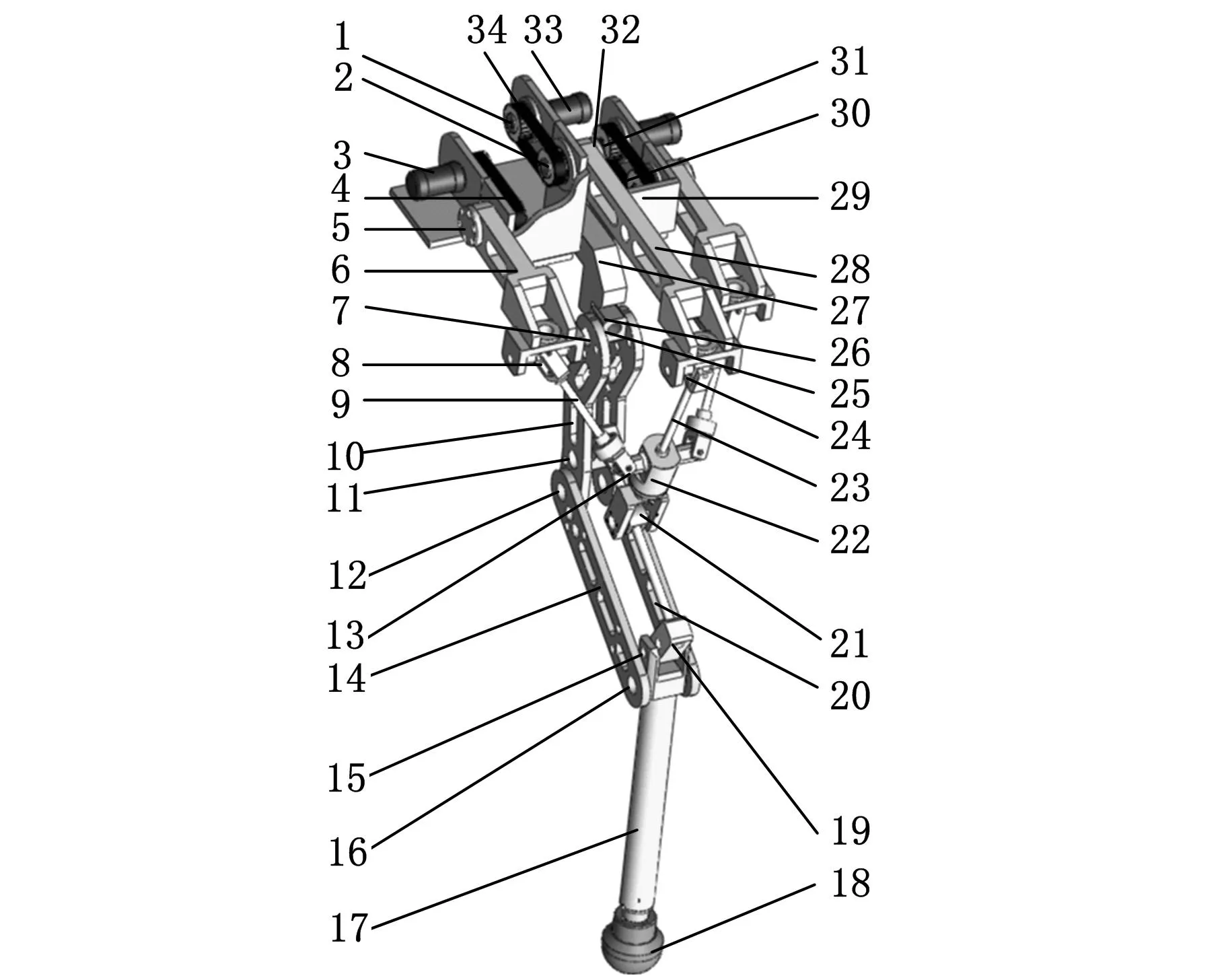
1.主输入带轮　2.主输出带轮　3.辅驱动电机　4.辅支链同步带　5.辅驱动轴　6.辅支链杠杆　7，11，12，15，16，25.转动副　8. 辅支链虎克铰　9.第一连杆　10.第二连杆　13.球副　14.第三连杆　17.小腿　18.足　19.第四连杆　20.第五连杆　21.等效球副　22.动平台　23.第六连杆　24.主支链虎克铰　26.转动块　27.连接座　28.主支链杠杆　29.机架　30.辅支链输出带轮　31.辅支链输入带轮　32.主驱动轴　33.主驱动电机　34.主支链同步带图3　腿部结构示意图

在腿部各构件连接方面，辅驱动电机3通过法兰与机架29固接，其轴端依次通过辅支链输入带轮31、同步带4和辅支链输出带轮30与辅驱动轴5的一端连接。辅驱动轴5的另一端通过螺栓与辅支链杠杆6连接；辅支链杠杆通过辅支链虎克铰8与第一连杆9相连；第一连杆通过球副13与动平台22相连；动平台与第六连杆23固接；第六连杆通过主支链虎克铰24 与主支链杠杆28相连；主支链杠杆与主驱动轴32一端螺栓连接。主驱动轴的另一端依次通过主输出带轮2、主支链同步带34和主输入带轮1与主驱动电机33的轴端连接。主驱动电机和机架29法兰连接；机架29与连接座27末端螺栓连接。

连接座的另一端通过转动副25与转动块26连接;转动块通过转动副7与第二连杆10连接；第二连杆通过转动副12与第三连杆14相连；第三连杆通过转动副16与小腿17相连。小腿末端与半球形足18固接，另一端通过转动副15与第四连杆19相连。第四连杆与第五连杆20固接，并通过转动副11与第二连杆10相连。第五连杆通过等效球副21与动平台22相连。其中第三连杆14、小腿17、第四连杆19与第五连杆20构成平行四边形机构。

2　腿部机构运动学分析

2.1坐标系的建立与动平台姿态描述

在图2中,RDi(i=1,2,3)表示转动副中心点,Ui(i=1,2,3)表示虎克铰中心点,Si(i=1,2)表示球副中心点,G表示RU支链与动平台的固接点,S表示等效球副中心点,即FD机构的运动输入点,Ri(i=1,2,3,4,5)表示FD机构的各杆件之间的转动副中心，H表示FD机构与机架连接转动副中心点,C表示足端点。设机构的主要几何参数为UiSi=li(i=1,2),U3G=l3,R4R1=l4,R1R3=l5,R1R2=l6,R5C=l7,GS=l8,SiG=a,RD1RD3=b,R1S=c。

建立基础坐标系O0x0y0z0,其中O0位于RD1和RD2连线的中点，x0轴沿RD1和RD2中心的连线,方向由RD2指向RD1,z0轴方向竖直向上,y0轴由右手定则确定,如图2所示。动坐标系Gxdydzd的坐标原点固接于S1S2的中点G上,zd沿着杆GU3轴线方向向上，xd轴方向由S2指向S1，yd轴由右手定则确定。为方便各支链连杆姿态描述，建立各支链参考坐标系Uixiyizi(i=1,2,3)，其中xi轴与相应支链虎克铰靠近杠杆的转动轴线重合，yi轴与RDi和Ui连线平行，方向由RDi指向Ui的方向，zi轴由右手定则确定；同时建立各支链连杆连体坐标系Uieifigi(i=1,2,3)，如图2所示，其中fi轴与相应支链虎克铰远离杠杆的转动轴线重合，gi轴与相应支链连杆轴线重合且方向向下，ei轴由右手定则确定。建立参考坐标系Hx4y4z4，坐标原点固接于H转动副的中心，其中y4轴的方向和y0轴方向相同,x4轴的方向为垂直于平形四边形机构所在平面向外，z4轴方向由右手法则确定。

根据机构分析和坐标系的建立,参考坐标系Uixiyizi的姿态相对于基础坐标系的姿态为绕x0轴旋转θpi(i=1,2,3)，连体坐标系Uieifigi相对于参考坐标系Uixiyizi的姿态为经过两次旋转得到,即绕xi轴旋转αti，绕fi轴旋转βi,用Rot函数表示，由此得i支链连杆的姿态矩阵为

Ri=Rot(x0,θpi)Rot(xi,αti)Rot(fi,βi)=

[eifigi]

(1)

gi=(gix，giy，giz)Ti=1,2,3

(2)

式中,ei、fi和gi分别为ei、fi和gi的3×1型单位矢量；gix、giy、giz为单位矢量gi在x、y、z方向的分量。

由此得第i支链连杆姿态角为

(3)

由以上姿态角分析得,RU支链连杆的末端和动平台固接,为了便于分析,最终选取G作为动平台参考点。

设三个转动副分别为RDi(i=1,2,3),且将其作为驱动输入点，设ni(i=1,2,3)为驱动杠杆的单位方向矢量，mi(i=9,10,11)分别表示杠杆RDiUi的杆长，则有

(4)

其中，ni=(0，cosθpi，sinθpi)T；θpi表示驱动副的角位移；lRDiUi表示杠杆RDiUi在固定坐标系下的长度矢量。

2.2位置反解分析

位置反解即已知足端点在基础坐标系中的位置矢量C=(xC，yC，zC)T,求解各个转动副的角位移。对于并联驱动机构,在基础坐标系O0x0y0z0中,设动平台参考点位置矢量G=(x0，y0，z0)T,根据机构几何条件，得矢量方程为

G=u3+L3=m3n3+RD3+l3g3

(5)

G=ui+Li-ai=mini+RDi+ligi-R3a0i

(6)

i=1,2

式中,ui、Li(i=1,2,3)分别为支链i在基础坐标系O0x0y0z0中的虎克铰中心点的位置矢量和连杆矢量;li为i支链连杆杆长;a0i为球副中心点Si在动坐标中的位置矢量;ai为球副中心点Si在固定坐标系中的位置矢量;RD3、RDi分别为RD3和RDi点在固定坐标系下的位置矢量。

对式(5)两边同时取范数得

l3=‖G-u3‖

(7)

g3=(G-u3)/l3

(8)

然后对式(6)两端同时取范数得

li=‖G-ui+ai‖i=1,2

(9)

gi=(G-ui+ai)/li

(10)

最终联合式(1)～式(10)得矢量G和转动副的角位移(θp1，θp2，θp3)T之间的关系。

对于串联执行机构,在参考坐标系Hx4y4z4中,设足端点C和输入点S的位置矢量分别为C0=(xC0，yC0，zC0)T和S0=(xr0，yr0，zr0)T,根据平面机构几何关系得

(11)

式中,θ1、θ2分别为杆l4、l6相对x4轴转过的角度。

参考坐标系Hx4y4z4相对于基础坐标系O0x0y0z0的姿态为绕y4轴经过一次旋转,其姿态矩阵为

R4=Rot(y3,θ3)

(12)

由上述坐标变换关系得,C0和S0在基础坐标系中的关系式为

C=R4C0+H

(13)

S=R4S0+H

(14)

式中,S、C、H分别为S、C、H在基础坐标系中的位置矢量。

由式(11)得

S0=f(C0)

(15)

f表示C0和S0之间的位置映射关系,篇幅所限不作展开。

由式(12)～式(15)得,点S和点C位置矢量关系为

(16)

其中，θ3和位置矢量C的x分量一一对应，可以通过式(13)求得。

建立两机构之间的关系为

S=L8+G=R3SG+G

(17)

式中,SG为输入点S在动坐标系中的矢量表示；L8为向量GS在基础坐标系中的矢量表示。

由式(16)、式(17)得足端点位置矢量C和参考点位置矢量G之间的关系,再结合上述矢量G和转动副的角位移(θp1，θp2，θp3)T之间的关系，从而确定3个转动副的角位移(θp1，θp2，θp3)T。

2.3速度映射分析

速度映射是指足端点C的速度与各支链转动角速度之间的映射关系，速度映射分析的目的在于得出速度雅可比矩阵，从而进行运动学传递性能分析[14-15]。

在式(5)和式(6)两端同时对时间求导得

(18)

(19)

(20)

(21)

(22)

由式(20)～式(22)得并联驱动机构转动副的角速度和动平台参考点速度的映射关系，写成矩阵形式为

(23)

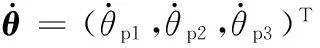
对于FD机构,式(13)两边同时对时间求导得

vC=w4×R4C0=w4×(C-H)

(24)

式中,w4为FD机构绕y3轴转动的角速度；vC为足端点在基础坐标系中的速度。

引入向量(C-H)的叉乘反对称阵A,由式(24)得

w4=-A-1vC

(25)

对式(16)和式(17)两端分别对时间求导，合并，得

(26)

式中,J0为位置映射f对应的速度映射关系。

3　2RUS+RU+FD机构工作空间分析

2RUS+RU+FD机构的工作空间为足端点C在实际运动过程中扫过的所有空间点的集合[16-18]。

3.1结构约束分析

对于该机构,转动副摆角约束,虎克铰与球铰的转角约束,三条支链连杆之间的干涉约束共同决定了工作空间的大小及形状。

转动副摆角约束为

θimin≤θi≤θimaxi=1,2,3

(27)

其中，θimin和θimax分别为第i条支链转动副摆角的最大、最小边界。

虎克铰转动时受到一定的限制，虎克铰允许连杆摆动的最大摆角为ψmax，ψmax由虎克铰的结构决定，当处于特定位姿时，杆向量与支座轴线之间的夹角ψi应满足条件：

ψi≤ψmax

(28)

球铰由于其自身的结构特点,转角范围受到一定的限制,nSi(i=1,2)表示球铰的基座在基础坐标系中的单位姿态向量,LSi表示连杆在基础坐标系中的单位姿态向量,设球铰的最大转角为θSmax，球铰链的结构转角

θSi=arccos(nSi·LSi)i=1,2

(29)

设初始姿态时球铰链的转角为0°,球铰的转动条件为

0°≤θSi≤θSmax

(30)

式中,θSmax为球副的最大转角。

腿部在运动过程中，机构中的各支链杆件会发生相互干涉，设各杆件直径均为D,杆件之间的最小距离为Dzxi(i=1,2,3)，则杆件之间不发生干涉的条件为

Dzxi≤Di=1,2,3

(31)

3.2工作空间形状分析

根据机器人整体平衡性能要求，设主辅支链杠杆之间竖直距离为h1,H点到O0点的竖直距离为h2,腿部机构的初始主要几何参数为l1=l2=195 mm,l3=245 mm,m1=m2=200 mm,m3=370 mm,a=55 mm,l4=200 mm,l5=50 mm,l6=300 mm,l7=450 mm,l8=160 mm,b=276 mm,c=110 mm,θSmax=45°,ψmax=60°,h1=70 mm,h2=55 mm。

根据以上几何参数,综合式(5)～式(17),在满足机构约束条件的情况下，利用极坐标搜索法绘制了该2RUS+RU+FD机构的足端点位置工作空间,如图4所示(图中色条表示高度方向的变化)。其中机器人在工作空间内腿部越障和跨步姿态如图5所示，图中L为步距，H为越障高度。

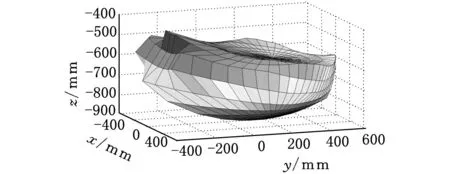
图4　腿部足端位置工作空间三维图

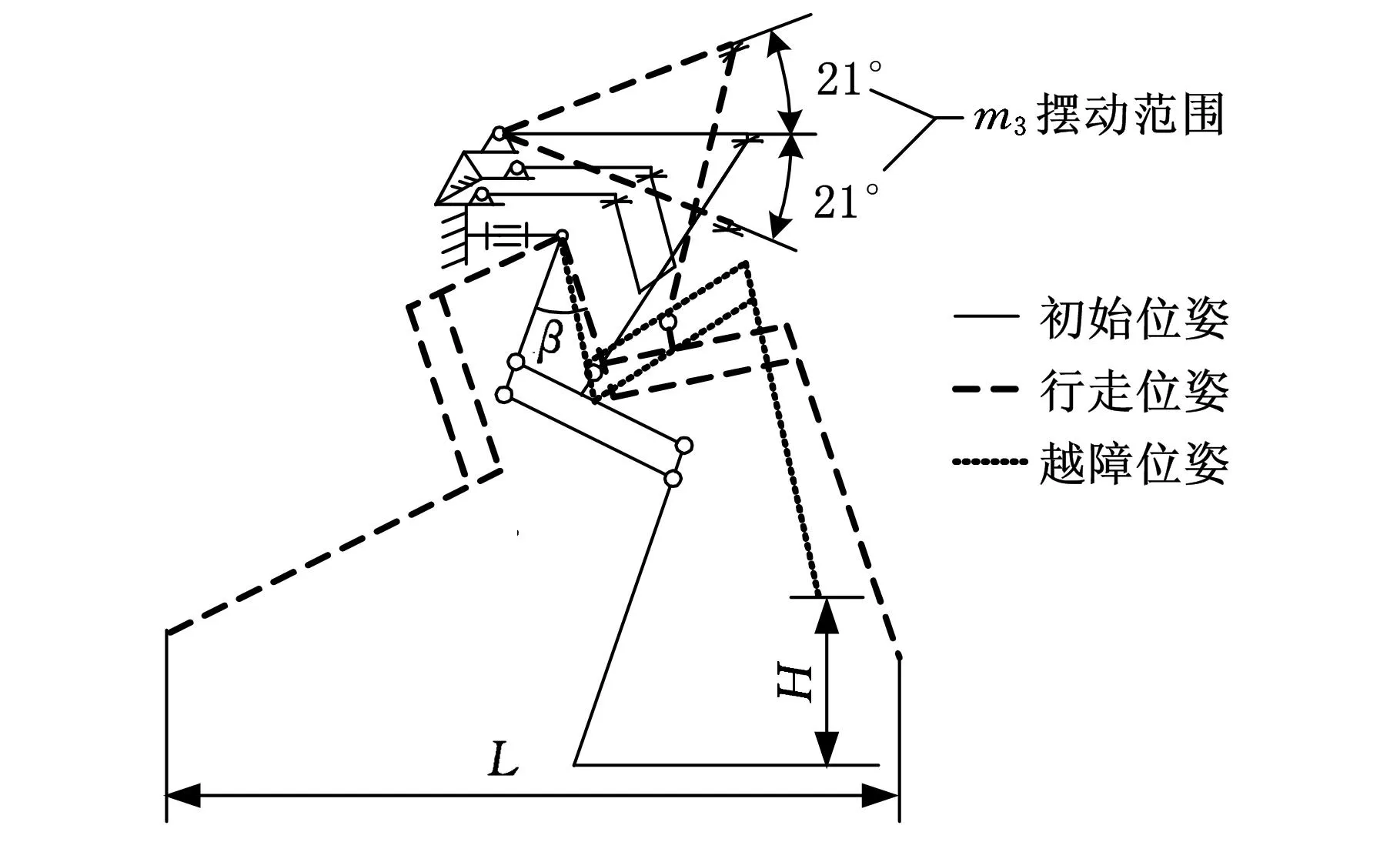
图5　跨步、越障腿部姿态示意图

从图4可知,足端工作空间在x轴方向(即腿部冠状面)对称分布；工作空间在y轴(即腿部矢状面) 正方向较大,且分布合理，基本满足机械腿步态要求。

为了进一步明确FD机构对工作空间形状的影响，定义标志量kV=V/Vb,其中V表示足端工作空间的体积，Vb表示并联驱动机构动平台的工作空间体积,基于上述几何参数得

kV=(3.7492×108)/(1.0017×107)=37.492

由此可知FD机构对工作空间的放大效果明显，有效提高了腿部机构的运动范围。

3.32RUS+RU驱动机构几何参数调整

工作空间的大小和分布又是衡量机器人运动能力的重要指标之一，一般用工作空间的最大高度Ht衡量机器人的越障能力，工作空间的最大长度Lt衡量机器人的步距和行走速度。然而，对该机构而言，驱动机构作为其核心部件，其几何参数设计的好坏对机器人运动性能有决定性的影响。 因此，本文将Ht、Lt作为2RUS+RU驱动机构主要几何参数的函数,得运动性能评价函数为

(32)

其中，Ht、Lt分别为越障能力、步距评价函数。

分析机构结构特点得θi和mi与腿部足端工作空间体积呈正相关,结合机器人整体尺寸设计要求,将其作为设计基准参数，因此，这里仅对工作空间影响较大的几何参数a、li(i=1,2,3)进行分析调整，利用单因素分析法，逐一分析其与Ht、Lt之间的关系，如图6所示。

然而对于消防机器人而言,其作业路况的复杂性往往成为其性能发挥的主要制约因素之一,这就对机器人的越障能力提出了极大的考验。因此,将工作空间最大高度作为调整的目标函数,根据图6所示关系,按l1→a→l3的次序,逐一调整逐一替代,得调整后工作空间如图7所示。

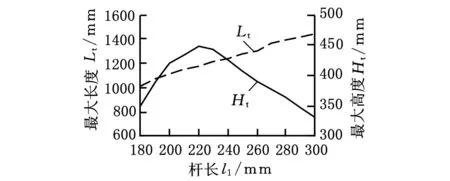
(a)杆长l1的影响

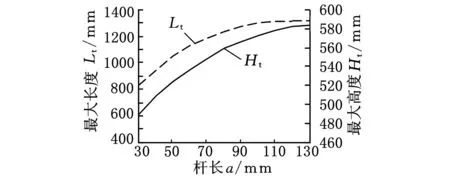
(b)杆长a的影响

(c)杆长l3的影响图6　几何参数对Ht、Lt的影响曲线

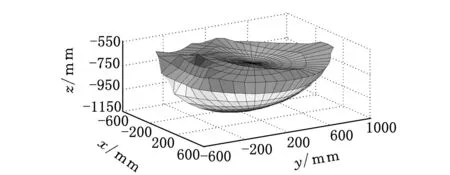
图7　参数调整后的工作空间

对比参数调整前后工作空间可得,工作空间的最大高度提高明显，同时,通过图5姿态分析表明,参数调整后,m3在同样摆动范围内摆动时,β角增大,越障高度增大,从而进一步提高了机器人的越障能力和对复杂环境的适应性,为机器人顺利完成消防任务提供了保障。

通过分析图6中几何参数a对Ht的影响曲线可知：a>130 mm时曲线变化减缓，并逐渐趋于水平,对工作空间的高度Ht影响不明显，因此,进一步考虑机器人整体尺寸与重量的要求，最终取a=55 mm；对于li(i=1,2,3)，根据图6中li对Ht的影响曲线,选取使Ht接近最大时对应的值，最终选取l1=l2=220 mm,l3=250 mm,其余几何参数按初选几何参数赋值，由此得参数调整后腿部主要技术参数如表1所示。

表1　腿部机构主要技术参数

4　结束语

本文提出的一种基于并联结构腿的新型六足机器人可防护性好，能应用于消防、核电、地震等诸多领域。提出了一种2RUS+RU+FD并联腿部机构,分析了该机构的运动学和工作空间，并针对消防机器人越障能力要求高的特性，给出了一组性能较优的机构几何参数。分析结果表明：2RUS+RU+FD机构运动学特性好，工作空间大，连续性好，满足腿部主体运动要求，适合作为消防机器人腿部机构。本文研究的成果为该机器人的实用化奠定了理论基础，为进一步开拓并联机构的研究领域和扩大并联六足机器人的应用范围提供了参考。

[1]刘静,赵晓光,谭民.腿式机器人的研究综述[J].机器人,2006,28(1):81-88.

Liu Jing,Zhao Xiaoguang,Tan Min.Legged Robots a Review[J].Robot,2006,28(1):81-88.

[2]陈学东. 多足步行机器人运动规划与控制[M].武汉:华中科技大学出版社,2006.

[3]张明路,彭平,张小俊.特殊环境下服役机器人发展现状及其关键技术研究[J].河北工业大学学报,2013,42(1):70-75.

Zhang Minglu,Peng Ping,Zhang Xiaojun.A Study of the Recent Development and Key Technologies of Advanced Robots Served in Special Circumstances[J].Journal of Hebei University of Technology,2013,42(1):70-75.

[4]Humphrey C M,Adams J A.Robotic Tasks for Chemical Biological,Radiological,Nuclear and Explosive Incident Response[J].Advanced Robotics,2009,23(9):1217-1232.

[5]Bogue R.Robots in the Nuclear Industry:a Review of Technologies and Applications[J].Industrial Robot,2011,38(2):113-118.

[6]张涛.基于改进粒子群算法的灭火机器人路径规划研究[D].西安:西安科技大学, 2011.

[7]卢超.一种基于粒子群算法的避障消防自动化小车[D].长沙:中南大学,2012.

[8]徐文福,毛志刚.核电站机器人研究现状与发展趋势[J].机器人,2011,33(6):758-767.

Xu Wenfu,Mao Zhigang.Research Status and Development Trend of Nuclear Power Plant Robots[J].Robot,2011,33(6):758-767.

[9]刘吉兆,刘轩昂,陈丰峰,等.仿生越障探测车的研制[J].中国机械工程,2012,23(14):1663-1666.

Liu Jizhao, Liu Xuanang, Chen Fengfeng, et al. Development of Bionic Obstacle-surmounting Rover[J].Chinese Journal of Mechanical Engineering, 2012, 23(14): 1663-1666.

[10]尹文英, 宋大祥, 杨星科, 等. 六足动物(昆虫)系统发生的研究[M].北京:科学出版社,2008.

[11]荣誉,金振林,崔冰艳.六足农业机器人并联腿构型分析与结构参数设计[J].农业工程学报,2012(15):9-13.

Rong Yu,Jin Zhenlin,Cui Bingyan.Configuration Analysis and Structure Parameter Design of Six-leg Agricultural-robot with Parallel-leg Mechanisms[J].Transactions of the Chinese Society of Agricultural Engineering,2012(15):9-13.

[12]黄真, 赵永生, 赵铁石. 高等空间机构学[M].北京：高等教育出版社，2006.

[13]田兴华, 高峰, 陈先宝, 等. 四足仿生机器人混联腿构型设计及比较[J].机械工程学报,2013,49(6):81-88.

Tian Xinghua, Gao Feng, Chen Xianbao, et al. Mechanism Design and Comparison for Quadruped Robot with Parallel-serial Leg [J].Journal of Mechanical Engineering, 2013, 49(6): 81-88.

[14]Yan C,Gao F,Zhang Y.Kinematic Modeling of a Serial-parallel Forging Manipulator with Application to Heavy Duty Manipulations[J].Mechanics Based Design of Structures and Machines,2010,38(1):105-129.

[15]齐明,刘海涛,梅江平,等.3-PUS/PU 3自由并联机构运动学优化设计[J].天津大学学报,2007,40(6):649-654.

Qi Ming,Liu Haitao,Mei Jiangping，et al.Kinenatics Optimum Design of a 3 DOF Parallel Mechanism with 3-PUS/PU Architecture[J].2007,40(6):649-654.

[16]Ma J,Huang Q,Xiong H,et al.Analysis and Application of the Singularity Locus of the Stewart Platform[J].Chinese Journal of Mechanical Engineering,2011,24(1):133-140.

[17]赵铁石, 陈江, 王家春,等. 4-UPU并联机器人机构及其运动学[J]. 中国机械工程,2005,16(22):2034-2037.

Zhao Tieshi,Chen Jiang,Wang Jiachun,et al.4-UPU Parallel Manipulator Mechanism and Kinematics[J].Chinese Journal of Mechanical Engineering,2005,16(22):2034-2037.

[18]熊有伦,丁汉,刘恩沧.机器人学[M].北京：机械工业出版社,1993.

(编辑王旻玥)

A Firefighting Six-legged Robot and Its Kinematics Analysis of Leg Mechanisms

Jin Zhenlin1,2Zhang Jinzhu1Gao Feng2

1.Yanshan University,Qinhuangdao,Hebei,066004 2.State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University,Shanghai,200240

Firstly,a six-foot parallel firefighting robot was proposed and the whole conceptual design was accomplished.Secondly,based on the evolution of 2UPS+UP parallel mechanism,a novel three degrees of freedom leg mechanism with self-protection function was proposed.Then,leg mechanism kinematics was analyzed and the equation for inverse position and velocity mapping relationship were presented. The workspace of manipulator was analyzed and its three-dimensional graphic was drawn.At last,the influences of drive mechanism geometrical parameters on obstacle ability and walking speed were revealed,and a reasonable set of graphical parameters was designed.The hexapod robot proposed herein has good protective properties and broad application prospects especially in fire, nuclear plant leak,earthquake and other disaster relief.

three degrees of freedom;hexagon robot;kinematics;workspace

2015-05-05

国家重点基础研究发展计划(973计划)资助项目(2013CB035501);机械系统与振动国家重点实验室重点实验室开放课题资助项目(MSV201506)

TP242DOI：10.3969/j.issn.1004-132X.2016.07.003

金振林,男,1962年生。燕山大学机械工程学院教授、博士研究生导师,上海交通大学机械系统与振动国家重点实验室教授。主要研究方向为并联机器人技术及应用。发表论文80余篇。张金柱,男,1989年生。燕山大学机械工程学院博士研究生。高峰,男,1956年生。上海交通大学机械与动力工程学院教授、博士研究生导师。