新型并联柔性铰链微动精密平台的研究

李仕华　韩雪艳　马琦翔　李富娟

燕山大学河北省并联机器人与机电系统实验室，秦皇岛，066004



新型并联柔性铰链微动精密平台的研究

李仕华韩雪艳马琦翔李富娟

燕山大学河北省并联机器人与机电系统实验室，秦皇岛，066004

基于3-PRC并联机构提出一种由压电陶瓷驱动的新型3-PRC并联微动平台，并进行了构型优化设计；采用矢量法对该平台的位置进行分析，并给出了该平台的理论耦合性误差；采用有限元对其运动解耦性进行了研究。最后制作了实验样机，并进行了实验测试。研究结果表明，该并联微动平台可以实现微米级三维移动，具有较高的精度和良好的运动解耦特性。

3-PRC；并联微动平台；解耦；三维移动

0　引言

随着计算机科技的迅速发展，设备微型化、微芯片高度集成化、操作精密微小化，使得微纳米技术成为国内外重点研究的方向，这就对高精度微操作系统提出了迫切的要求。而由微定位技术与并联机器人技术结合而产生的微动并联机器人技术成为新的发展方向[1]。

近年来，许多并联结构的微动机器人样机相继诞生。张旭辉[2]提出一种新型2-2-2正交6-RSS微动机器人模型；杨启志等[3]设计了一种非对称全柔性3-RRRP微动并联激振台机构；贾晓辉等[4]基于Delta机构设计并制造出了可以实现三维移动的3-RRPR精密定位平台，利用矢量闭环法建立了其速度、加速度方程，并采用虚功原理进行了动力学分析；李仕华等[5]提出了一种新型3-RRRRR并联微动机构，能够实现三维解耦纳米级的移动。新加坡南洋理工大学的Vahid等[6]研制出一种由压电陶瓷驱动的三自由度锥形并联微动机构，三个压电陶瓷分别装在空间对称分布呈120°角度的分支连杆上，可以实现空间三维移动。

为了丰富并联微动机构的构型，本文基于3-PRC并联机构，通过柔性铰链代替传统运动副消除机械摩擦和间隙方法，设计出一种由压电陶瓷驱动的新型3-PRC并联微动平台，该平台采用桥式位移放大机构，可实现较大微米级的三维移动，具有结构紧凑、精度较高、良好输入-输出线性关系和运动解耦优点，便于控制，具有非常好的应用前景。

1　平台的构型

1.1初始构型设计

3-PRC微动平台初始构型如图1所示。将3-PRC并联机构[7]的三条分支中圆柱副C等效为转动副R和移动副P，并分别用平行四杆式柔性移动副P、柔性转动副R进行等效替换；第一个移动副P由直推式结构的柔性移动副P进行替换，并将三条分支在空间正交布置。

图1　微动平台初始构型

1.2构型的优化设计

为使其结构更加紧凑、工作空间更大和具有良好解耦特性，对初始构型进行优化，主要的优化过程如下：

(1)主动输入移动P副优化。为了克服压电陶瓷输入位移小的缺点，采用桥式位移放大机构[8-9]替代薄片弹簧式移动副，如图2a和图2b所示，以便增大整个微动平台的工作空间；其中，桥式位移放大机构一端固定，另一端输出，通过柔性铰链变形使得横向输入位移转换成纵向输出位移，并且输出位移大于输入位移，起到位移放大作用。

(2)转动R副和圆柱C副优化。由于C副等效为一个R副和一个P副，这样在初始构型中的两个R副连接处的应力比较大，容易发生断裂，所以将其置换成R-R复合转动副，通过有限元仿真结果可知，两个支链较单支链的强度有所提高，不易断裂，如图2b所示。

(3)重新组合优化。将被动移动副P与R-R复合转动副进行合并，组成一个含8个R副的柔顺机构，如图2c所示。这个机构的优点就是可以实现两个伴随运动方向上的被动移动，有利于实现整个微动平台的解耦。最后，将桥式位移放大器放到柔顺机构的内部，结构就更加紧凑，刚度更大。图2中，PZT代表压电陶瓷。

(a) (b)(c)图2　微动平台分支优化

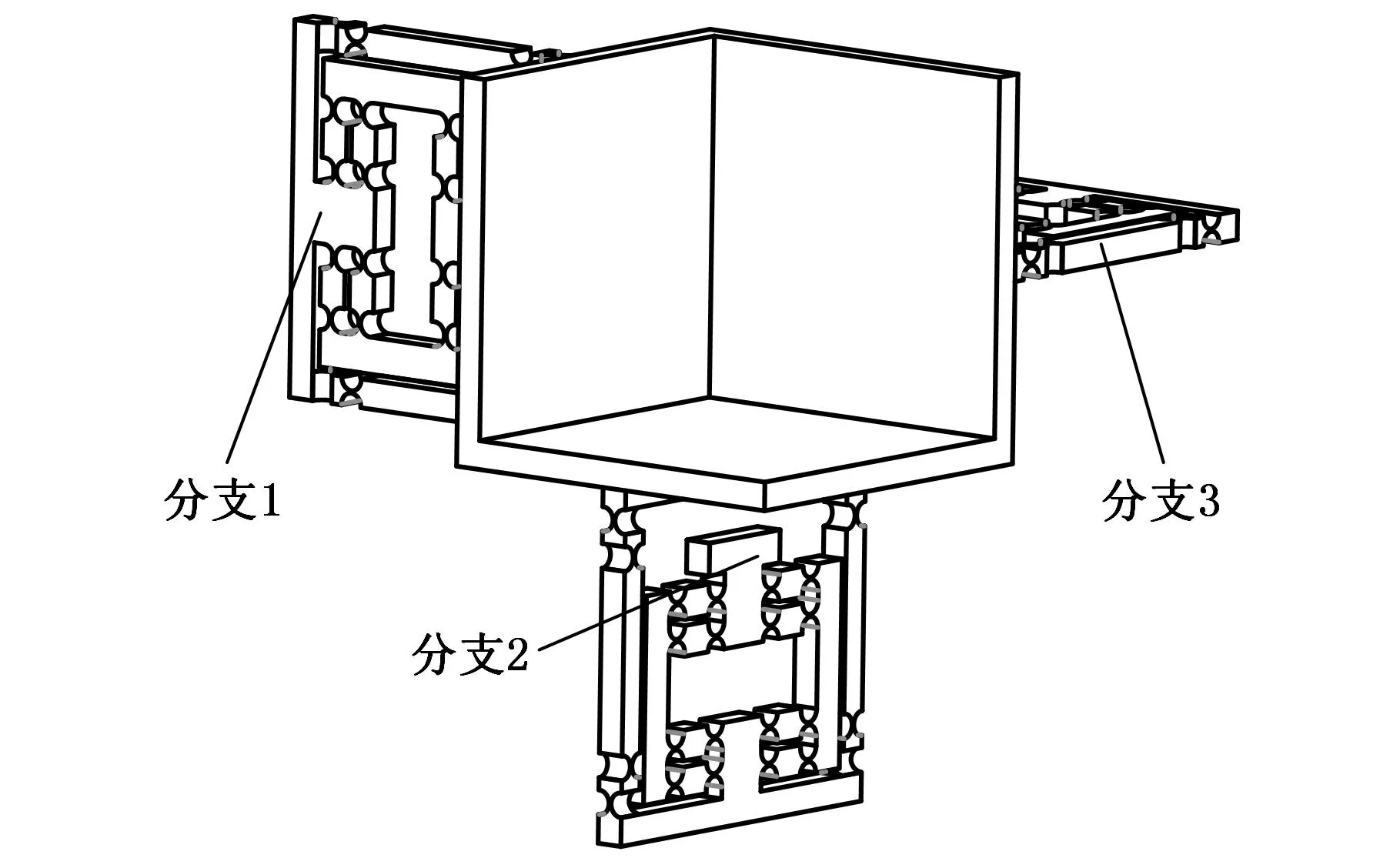
图3　微动平台最终构型

图3所示为3-PRC并联微动平台优化后的三维构型。整个微动平台的材料采用超硬铝，弹性模量E=74 GPa，屈服强度σ=550 MPa，泊松比μ=0.33。以获取更大的放大机构的放大比为优化目标，考虑加工装配能力，确定柔性铰链的半径R=3 mm，最薄处厚度t=0.6 mm，整个微动平台的外形尺寸为200 mm×200 mm×200 mm。平台的固有频率为72 Hz，能够避免共振(压电陶瓷的工作频率不大于20 Hz)，保证其稳定位移输出。

2　运动学位置分析

2.1平台的位置反解

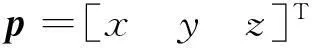
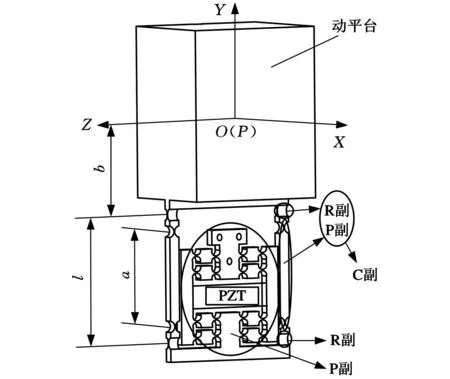
图4　微动平台分支i结构

根据图5所示的位置矢量关系，可以得到第i条分支的矢量方程：

lli0=Li-didi0

(1)

Li=p+bi-ai

其中，l为沿着向量CiBi方向的长度，li0为向量CiBi方向上的单位向量，di为第i条分支移动副输出位移量，di0为第i条分支移动副输出位移方向上的单位向量，ai和bi分别为点Ai和点Bi在相对初始位置下的位置矢量。另外，Ai为第i条分支的在初始位置下移动副输出端，Bi为第i条分支的R副轴线中心点，Ci为位置发生变化后第i条分支的移动副输出端的位置。

图5　矢量示意图

根据式(1)，可以得到

(2)

将式(2)展开为如下形式：

(3)

由于x、y、z和di远小于l，这样就可以将式(3)推导为

(4)

式(4)可写为d=-Ip，根据d=Aq，反解为

(5)

由此可见，该微动平台可以实现近似解耦的三维平移运动。

2.2平台的位置正解

对式(5)两边都乘以转换矩阵I的逆矩阵，运动学正解方程为

p=-AIq

(6)

其中，桥式位移放大机构的放大比A=4。

2.3平台的耦合性误差分析

平台在三维移动方向是近似解耦的，存在耦合性误差。以对分支2进行加载输入位移为例，对其耦合误差进行理论分析。

假设对分支2由压电陶瓷驱动的移动副P输出位移为d2，其他分支输入位移为0，在分支1上就会产生沿-X方向的伴随位移e11，而在分支3上会产生沿-Z方向的伴随位移e32，如图6所示，可计算出由分支1、3的耦合误差:

(7)

其中，β1=arcsin(d2/l)≈d2/l，α3=arcsin(d2/a)≈d2/a。可进一步得到

(8)

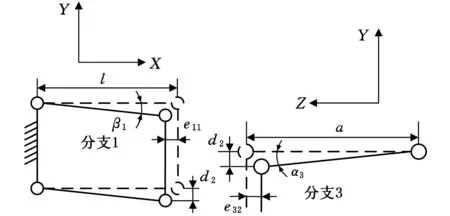
图6　耦合误差示意图

2.4平台的有限元分析

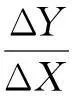
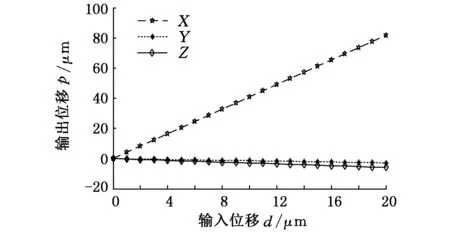
图7　分支1仿真位移曲线

(2)三个分支同时加载，设同时输入位移为0～20μm，动平台的三个平面中心点处沿X、Y、Z轴的位移量如图8所示。由图8可知，当三个分支同时加载位移时，平台在X、Y、Z轴方向上都有位移输出，且输出位移与输入位移成线性关系，说明该平台是近似解耦的，与理论分析结果一致。其中最大位移量分别为82.530μm、90.435μm和83.759μm；分支1、分支2、分支3斜率的平均值分别为4.019、4.396、4.188。X、Z轴方向输出位移近似一致，而Y轴方向输出位移与X、Z轴有差异，这种差异的出现与分支2沿重力方向布置有关。

图8　3个分支仿真位移曲线

3　并联微动平台的实验研究

根据上文选定的机构参数，制作3-PRC微动平台实验样机，如图9所示。在每个分支的第一个柔性移动副处安装了德国进口封装式压电陶瓷驱动器(型号为Pst150/7/ 20VS12，最大推力为1800 N，标称位移为20μm)；选用精度为满量程0.1%的闭环压电陶瓷控制器和最大量程为-500～500μm、线性度为满量程±0.25%、精度小于10 nm的LVDT测微仪测量平台输出位移。

图9　实验样机

实验时，如图10所示，将测微仪测头与动平台X、Y、Z轴三个方向平面的中心位置相接触，利用压电陶瓷控制器加载位移，并通过测微仪记录输出端的位移量，每次重复做三组实验。

图10　微动平台实验

(1)分支1加载。在0～20μm范围内对分支1进行加载，测量动平台沿X、Y、Z轴方向的输出位移，并绘制了位移输出曲线，如图11所示。

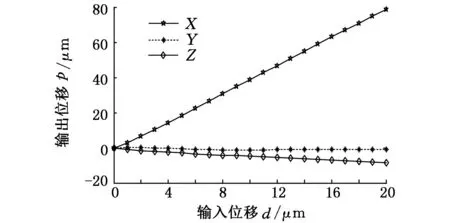
图11　分支1实验位移曲线

(2)三个分支加载。在0～20μm范围内对3个分支同时进行加载，测量动平台沿X、Y、Z轴方向的输出位移，并绘制了位移输出曲线，如图12所示。

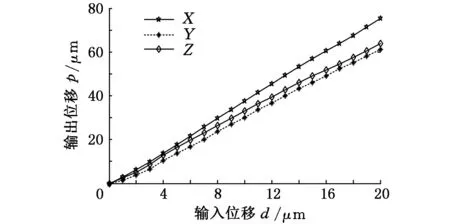
图12　3个分支实验位移曲线

由图12可知，当三个分支同时加载位移时，平台在X、Y、Z轴方向上都有位移输出，且输出位移与输入位移成线性关系，说明该平台是近似解耦的。其中最大位移量分别为75.213μm、61.000μm和63.733μm；分支1、分支2、分支3位移曲线的斜率的平均值分别为3.761、3.050、3.187。图12的结果与图8的仿真结果有一定差距，这是由实验样机加工对表面氧化发黑处理，使放大机构的放大比有所降低，以及在理论建模时进行近似简化而产生的原理误差，柔性铰链的圆弧半径、宽度、杆件厚度等加工以及装配时产生的误差，外界环境和测量产生的误差等原因造成的。

实验时分支1加载后，平台沿X轴方向输出位移(图11)与理论输出位移(式(6))的偏差角φ1为0.35798″，如图13所示；三个分支加载后，将图12中X、Y、Z轴方向的输出位移合成后，再与理论输出位移(式(6))进行比较，其偏差角φ2为331.56″(0.0921°)，如图14所示；在三个分支随机性加载情况下的平均值与三个分支输出位移最大值的偏差为0.98μm，如图15所示，微动平台的重复精度可以达到1μm。这说明平台的精度较好。

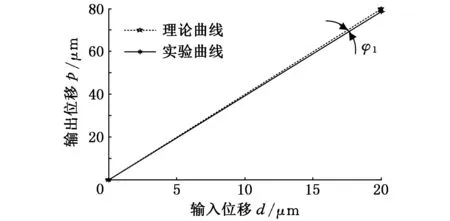
图13　分支1加载误差曲线

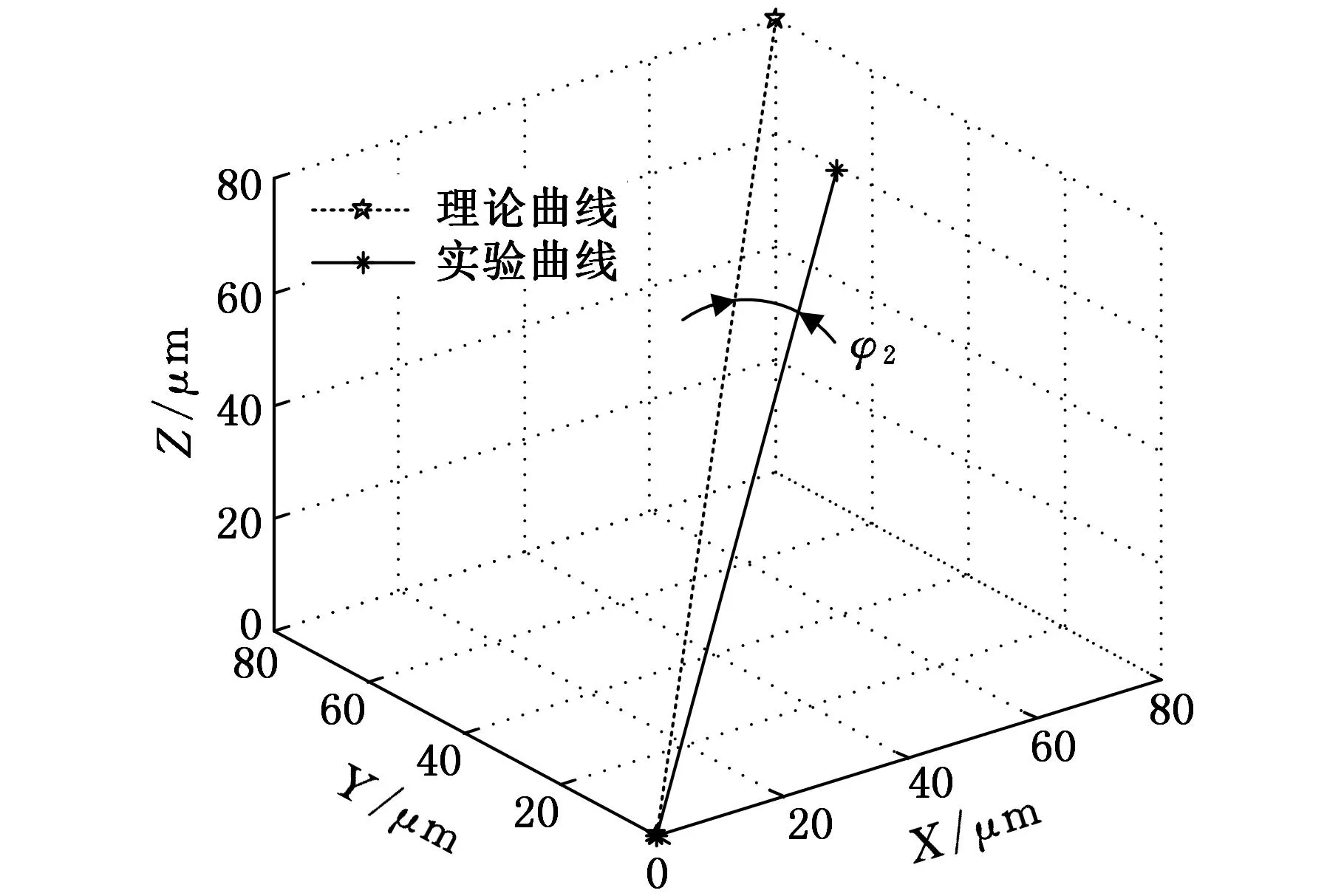
图14　三个分支加载误差曲线

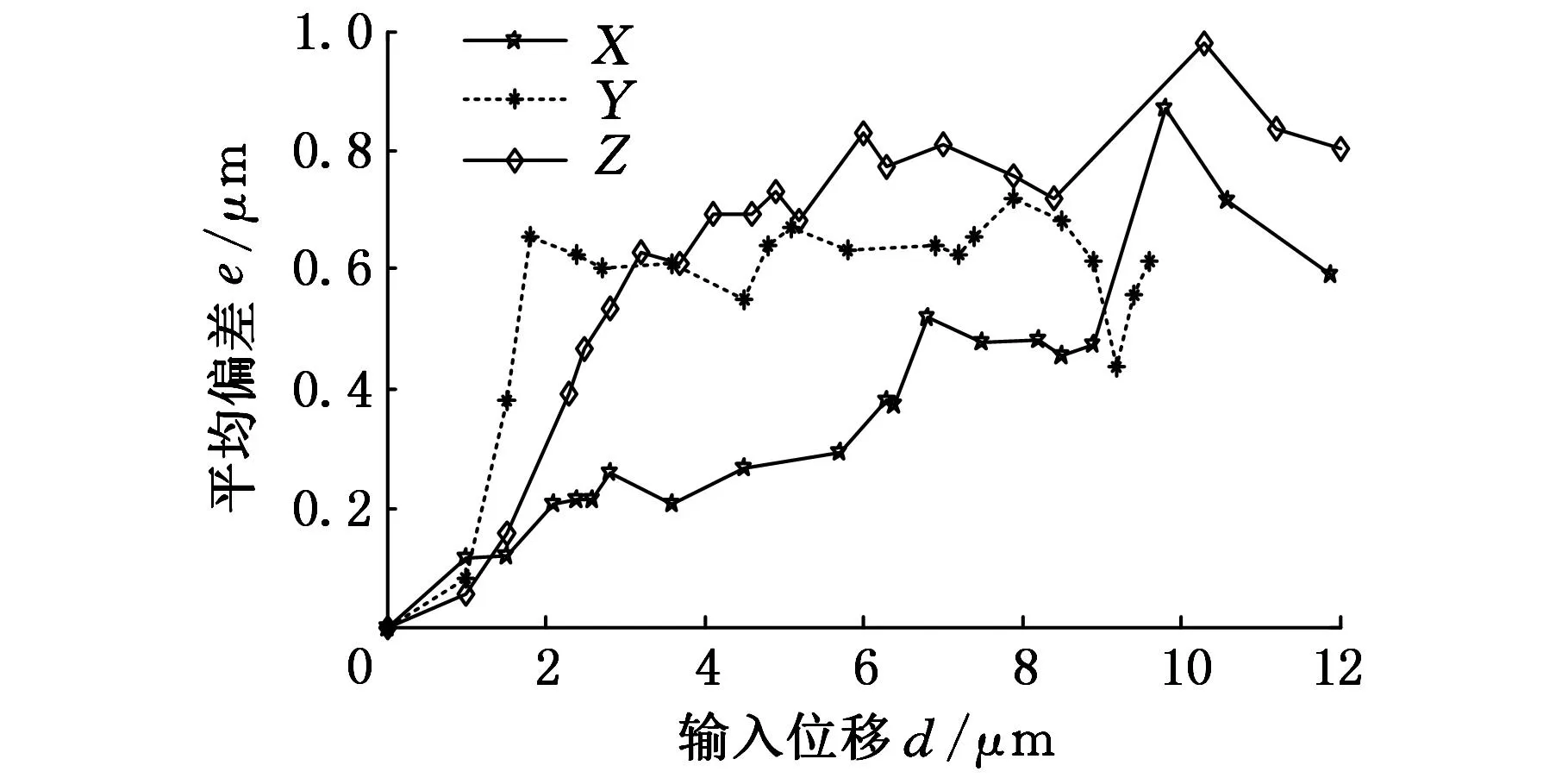
图15　随机性加载情况误差曲线

因此，实验结果与理论结果和有限元分析结果一致。该微动平台便于实现控制，具有较高的精度。

4　结束语

本文提出并设计了一种新型由压电陶瓷驱动的3-PRC并联精密微动平台；建立了该平台的位置正反解表达式和理论耦合性位移误差结果，并进行了有限元分析。最后制作了实验样机，并进行了实验测试。研究结果表明该并联微动平台可以实现较大的微米级三维移动，具有较高的精度、良好的线性输入-输出关系和运动解耦特性，具有非常好的应用前景。

[1]李杨民，汤晖，徐青松，等.面向生物医学应用的微操作机器人技术发展态势[J].机械工程学报，2011，47(23): 1-13.

Li Yangmin, Tang Hui, Xu Qingsong, et al. Development Status of Micromanipulator Technology for Biomedical Applications[J]. Journal of Mechanical Engineering, 2011, 47(23):1-13.

[2]张旭辉.新型六自由度并联微动机器人的分析、设计与加工[D].秦皇岛：燕山大学，2012.

[3]杨启志，庄佳奇，尹小琴，等.一种三自由度全柔性并联微动激振台的设计[J].机械设计与研究，2011，27(4): 23-27.

Yang Qizhi, Zhuang Jiaqi, Yin Xiaoqin, et al. Study on a Fully Compliant 3-DOF Parallel Micro-displacement Vibration Actuator[J]. Machine Design & Research, 2011, 27(4):23-27.

[4]贾晓辉，田延岭，张大卫，等.基于虚功原理的3-RRPR柔性精密定位工作台的动力学分析[J].机械工程学报，2011，47(1): 68-73.

Jia Xiaohui, Tian Yanling, Zhang Dawei, et al. Inverse Dynamics of 3-RRPR Compliant Precision Positioning Stage Based on the Principle of Virtue Work[J]. Journal of Mechanical Engineering, 2011, 47(1):68-74.

[5]李仕华，句彦儒，王志松，等.一种新构型3-RRRRR并联微动机构的研究[J].中国机械工程，2011，22(22): 2662-2666.

Li Shihua, Ju Yanru, Wang Zhisong, et al. Research on a Kind of New Structured 3-RRRRR Parallel Micromanipulator[J]. China Mechanical Engineering, 2011，22(22): 2662-2666.

[6]Vahid H, Tegoeh T. Dynamic Modeling of 3-DOF Pyramidal-shaped Piezo-driven Mechanism[J]. Mechanism and Machine Theory, 2013,70: 225-245.

[7]许佩霞.3-PRC并联机构运动学分析[J].机械设计，2009,1(26): 14-16.

Xu Peixia. Kinematics Analysis of 3-PRC Parallel Mechanism[J]. Journal of Machine Design, 2009, 26(1):14-16.

[8]叶果，李威，王禹桥，等.柔性桥式微位移机构位移放大比特性研究[J].机器人，2011，33(1): 252-254.

Ye Guo, Li Wei, Wang Yuqiao, et al. Analysis on Displacement Amplification Ratio of a Flexible Bridge-type Micro-displacement Mechanism[J]. Jiqiren/Robot, 2011, 33(2):251-256.

[9]Xu Q S, Li Y M. Analytical Modeling, Optimization and Testing of a Compound Bridge-type Compliant Displacement Amplifier[J]. Mechanism and Machine Theory, 2011(46): 183-200.

[10]毕树生，宗光华.Delta并联微操作手运动学的矢量法分析[J].北京航空航天大学学报，2003，29(4): 339-341.

Bi Shusheng, Zong Guanghua. Analysis of Kinematics of Delta Parallel Micromanipulator with Vector Space Method[J]. Journal of Beijing University of Aeronautics & Astronautics, 2003, 29(4):339-341.

[11]Li Yangmin，Xu Qingsong. Design and Optimization of an XYZ Parallel Micromanipulator with Flexure Hinges[J]. J. Intell. Robot Syst.， 2009， (55): 377-402.

(编辑郭伟)

Research on Novel Parallel Micro-motion Precision Platform with Flexible Hinge

Li ShihuaHan XueyanMa QixiangLi Fujuan

Parallel Robot and Mechatronic System Laboratory of Hebei Province, Yanshan University,Qinhuangdao,Hebei,066004

Based on 3-RPC parallel mechanism, a new 3-PRC parallel micro-motion platform driven by piezoelectric ceramic transducer was put forward and its structure was optimized. The position of the platform was analyzed by using vector method and the theoretical coupling errors of the platform were put out. The motion decoupling characteristics of the platform were researched and analyzed by using the finite element analysis method. At last the prototype was produced and tested. The results show that the parallel micro-platform can achieve three-dimensional movement with high precision and good motion decoupling characteristics in the micron scale.

3-PRC; parallel micro-motion platform; decoupling; three-dimensional movement

2015-05-19

河北省自然科学基金资助项目(E2013203293)

TP24DOI：10.3969/j.issn.1004-132X.2016.07.007

李仕华，男，1966年生。燕山大学教务处教授、博士研究生导师。主要研究方向为并联机器人技术及理论。发表论文70余篇。韩雪艳，男，1978年生。燕山大学机械工程学院博士研究生。马琦翔，男，1987年生。燕山大学机械工程学院硕士研究生。李富娟，女，1985年生。燕山大学机械工程学院实验员。