基于持续屈服节理模型的节理直剪数值试验

高艳华，吴顺川，王贺，肖术

（1. 北京科技大学 土木与环境工程学院，北京，100083；2. 北京矿冶研究总院，北京，100070；3. 长江三峡勘测研究院有限公司，湖南 武汉，430074）

基于持续屈服节理模型的节理直剪数值试验

高艳华1，吴顺川1，王贺2，肖术3

（1. 北京科技大学 土木与环境工程学院，北京，100083；2. 北京矿冶研究总院，北京，100070；
3. 长江三峡勘测研究院有限公司，湖南 武汉，430074）

根据山西平朔露天煤矿砂岩岩石及节理室内试验确定力学参数，采用块体离散元软件3DEC内置FISH语言编制程序，实现基于持续屈服节理模型的节理直剪数值试验，研究节理粗糙度、初始摩擦角和基本摩擦角差值对剪切强度的影响。研究表明：采用持续屈服节理模型的节理面数值剪切试验能反映节理剪切应力随剪切位移变化的4个阶段，即曲线上升—峰值—软化—残余应力阶段；与室内试验结果相比，持续屈服节理模型能较好地表征节理剪切峰值强度及峰值强度前剪切应力与剪切变形的非线性关系，且能较好地反映峰值强度后应变软化及残余强度等节理面力学性质；随粗糙度增大，剪切峰值强度按幂函数增大；随摩擦角差值增大，节理剪切峰值强度线性增大。

持续屈服节理模型；节理法向刚度；节理切向刚度；粗糙度；摩擦角；节理直剪试验

岩体是地质体，其力学性质由组成岩体的岩石、结构面和赋存条件决定［1］。节理作为一种重要的结构面，其力学性质对岩体力学性质以及岩体工程稳定性起重要作用。节理力学性质主要包括法向变形、剪切变形和抗剪强度［1］。国内外许多学者对节理力学性质进行了研究。GOODMAN等［2-3］提出采用“法向刚度”和“切向刚度”分别描述节理面法向应力和法向位移、剪切应力和剪切位移之间的关系，并通过节理法向力学试验得出法向应力与法向位移的非线性关系；BARTON等［4-5］由节理剪切试验得到节理剪切强度与节理面粗糙因子、抗压强度以及残余摩擦角等关系的经验公式；KULHAWAY［6］提出采用双曲线方程表征剪切峰值强度之前剪切应力与剪切位移非线性关系；BANDIS等［7］在板岩、玄武岩、石灰岩、粉砂岩及砂岩等不同岩性中的节理面法向加载试验和剪切试验基础上，研究了节理法向变形和剪切变形的特征，得出了法向应力-位移双曲线本构方程；赵坚［8］提出了节理吻合系数概念，并研究了其对节理力学性质的影响；杜时贵等［9-10］针对节理抗剪强度参数确定及综合评价进行了试验研究。此外，近年来，循环荷载下节理力学性质研究得到了较快发展。BANDIS等［7， 11］采用天然岩石节理进行法向循环加卸载试验，研究了节理法向循环加卸载力学性质；HOMAND等［12-15］采用天然节理或不同形态人工节理，进行节理循环剪切试验，研究了不同节理表面节理循环剪切力学性质；夏才初等［16］采用水泥砂浆人工节理进行不同法向应力下反复剪切试验，给出了考虑反复剪切次数对节理剪切强度公式。基于节理力学性质的研究，节理本构模型也得到了发展。目前，在岩体工程计算中，单向剪切加载下节理本构模型主要有2类，如图1所示。类型Ⅰ模型表征节理理想弹塑性力学行为，广泛用于岩体工程计算中［17-18］。块体离散元软件3DEC中库仑滑移节理模型（Coulomb slip joint model）属于类型Ⅰ。类型Ⅱ模型更能真实反映节理弹塑性力学行为，但因其力学参数多、计算复杂，在岩体工程中应用较少。类型Ⅱ模型目前已有几种数学表达式：CUNDALL等［19］根据玄武岩节理试件剪切试验结果提出持续屈服节理模型（continuously yielding joint model）；肖卫国等［20］提出剪胀和破坏耦合的节理岩体本构模型；唐志成等［21］提出硬化-软化全剪切本构模型。库仑滑移节理模型基于库仑摩擦准则，具有以下几个特点：1） 节理的法向、切向刚度为定值，节理刚度不随节理塑性位移累积而退化；2） 剪切峰值强度前节理剪切应力与剪切位移线性相关，节理表现为弹性力学行为；3） 在节理达到剪切峰值强度后，节理本构模型曲线维持剪切强度峰值，即残余强度与峰值强度相同。因此，库仑滑移节理模型不能表征节理刚度退化、剪切应力与剪切位移非线性关系以及节理剪切应力峰后力学行为。持续屈服节理模型将节理剪切应力随剪切位移的变化过程分为曲线上升—峰值—应变软化—残余强度4个阶段，如图1类型Ⅱ曲线所示，其能够表征节理剪切应力峰值前非线性力学行为及峰值后应变软化、残余强度等力学行为。此外，持续屈服节理模型还可实现循环加载，适用于解决爆破、地震等动力作用下节理动力响应问题。因此，持续屈服节理模型可更真实地反映节理力学性质，但未见国内应用文献。国外文献中，CUNDALL等［22］运用此模型进行了因开挖扰动引发不连续面不稳定滑移的数值模拟；MA 等［23］运用此模型分析了地震作用下节理岩体地下开挖工程的动力响应问题。本文根据山西平朔露天煤矿砂岩岩芯节理面直剪力学试验、磨光面剪切试验、单轴压缩试验等室内试验，获取力学参数，采用块体离散元软件3DEC内置FISH语言编制程序，进行基于持续屈服节理模型的节理直剪数值试验，并研究节理粗糙度、初始摩擦角和基本摩擦角差值对节理剪切强度的影响。

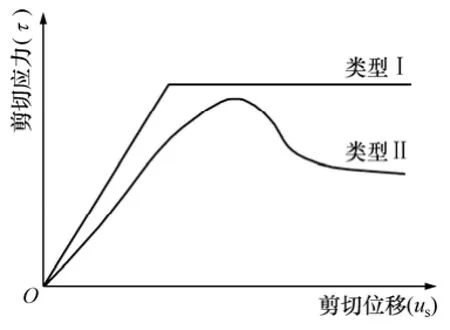
图1　节理剪切应力-位移本构模型Fig. 1　Shear stress-displacement curves of joint

1　持续屈服节理模型

在实际工程中，节理力学性质和加载路径均较复杂。在剪切荷载作用下，节理表现出渐进破坏、节理刚度与法向应力有关、随塑性剪切位移增加剪胀角降低等非线性力学特性。在工程扰动以及动力荷载（爆破荷载、地震作用等）作用下，节理受循环加卸载作用。持续屈服节理模型可较真实地反映节理非线性力学性质以及在复杂加卸载路径下的力学行为。用增量方式表示持续屈服节理模型的方程如下［24］：

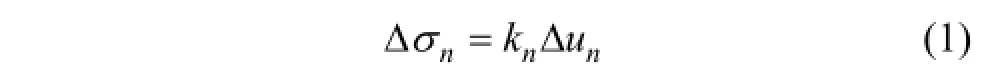
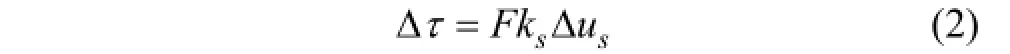
式中：Δσn和 Δτ分别为法向应力增量和剪切应力增量；kn和ks分别为节理法向刚度和切向刚度；F为切向刚度因子；Δun和Δus分别为法向位移增量和剪切位移增量。试验表明节理法向刚度、切向刚度与法向应力有关［6-7］，关系式可表示为：

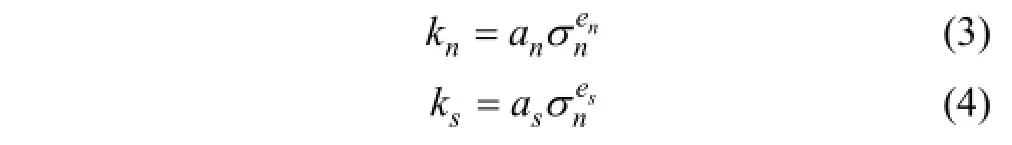
式中：an和as分别为节理法向刚度系数和切向刚度系数；en和es分别为节理法向刚度指数和切向刚度指数。在剪切荷载下，节理面磨损导致切向刚度随剪切位移增加非线性变化，持续屈服节理模型中采用节理切向刚度因子来表征刚度的非线性变化。切向刚度因子取决于图 2所示的剪切应力-位移曲线与剪切强度限值曲线［24］的距离，由下式求得：

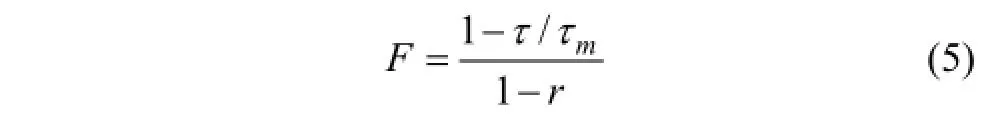
式中：τ为剪切应力；τm为节理剪切强度限值，即节理最大剪切强度；r为反向加载时弹性刚度恢复因子。r初始值为0，当反向加载时，r=τ/τm（此时F=1）；当剪切应力接近最大剪切强度时，为了避免数值噪专长，r≤0.75。剪切应力峰值前，F为小于1的正数，节理切向刚度退化；当剪切应力达到峰值即节理剪切强度达到剪切强度限值时，F为0；峰值后F变为负数，节理进入软化阶段，节理切向刚度绝对值随剪切位移增加而减小。

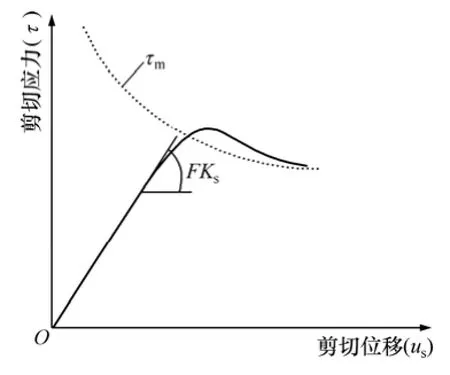
图2　剪切应力-位移曲线和剪切强度限值曲线［25］Fig. 2　Shear stress-displacement curve and bounding shear strength curves［25］

剪切强度限值随着剪切塑性位移累积呈非线性下降，且与节理粗糙度相关，能较真实地模拟节理渐进屈服。

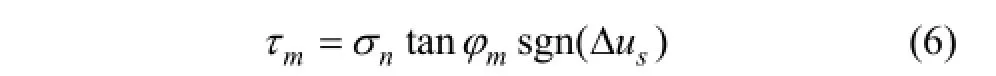
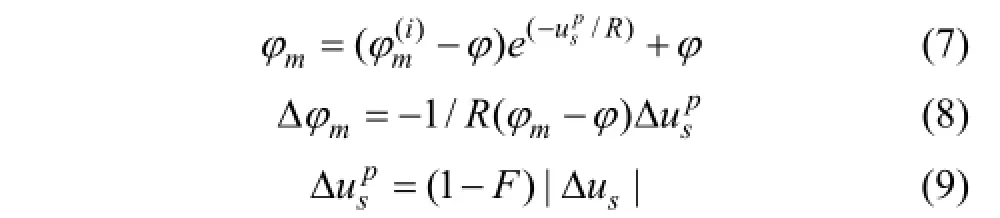
式中：σn为法向应力；φm为峰值摩擦角，即节理未损坏时的摩擦角或节理最大剪胀角时的摩擦角；为节理初始摩擦角，即峰值摩擦角φm的初始值，表征节理原位状态的摩擦角；φ为节理基本摩擦角；sgn（ ）为符号函数，表示取括号内变量的正负号，如在循环剪切中，当Δus为正数时，为1，反之为-1；为塑性剪切位移；R为采用长度单位表示的节理粗糙度。剪切强度限值 τm由式（6）确定，式（6）中峰值摩擦角 φm可由式（7）求得。式（7）表示节理峰值摩擦角在剪切过程中的磨损。式（7）的增量表达式为式（8），式（8）中塑性位移增量由式（9）定义。由式（8）可知，随节理塑性变形累积，峰值摩擦角逐渐减小。

在法向荷载、剪切荷载共同作用下，由于节理面微凸体的爬坡和啃断作用，节理产生一定程度的剪胀与磨损。节理的剪胀现象可由剪胀角表征，持续屈服节理模型中剪胀角i为节理剪切过程中摩擦角与基本摩擦角之差，由下式计算：

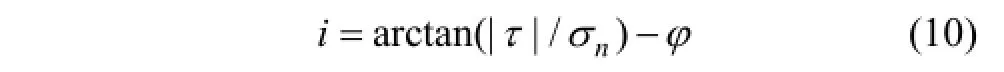
其中：i为节理剪胀角。在节理直剪试验中应用持续屈服节理模型可按以下步骤进行：

1） 由室内节理力学试验确定节理法向、切向刚度、节理初始摩擦角、基本摩擦角以及粗糙度等节理力学参数。

2） 计算剪切强度限值和切向刚度因子。在剪切应力峰值前，切向刚度因子为小于1的正值，节理刚度减小，剪切应力呈非线性增加。

3） 随着剪切位移增加，剪切应力逐渐接近剪切强度限值，如图2所示；当剪切应力大于等于剪切强度限值时，剪切应力达到峰值。

4） 剪切应力达到峰值后，节理切向刚度因子变为负值，剪切应力-位移曲线下降，进入应变软化阶段。

5） 随着剪切位移继续增加，剪切应力最终达到残余应力。

2　节理直剪试验

2.1节理直剪室内试验

节理直剪试验含1个节理面的岩芯试件，试件直径×高为60 mm×120 mm。该岩芯取自山西平朔露天煤矿，并通过蜡封保留天然状态下的节理面状态。采用岩石弱面直剪仪测定节理面剪切力学性质。试验前将节理面两侧岩芯试件分别放于直角边长为150 mm、高为130 mm的直三棱柱型模具中，采用C30混凝土浇筑成直三棱柱直剪试件，将两侧直三棱柱按照节理面原状对接成1个边长为150 mm的立方体试件。试件养护28 d后进行剪切试验。本次试验分10组进行，每组试件3个，共浇筑30个试件。在节理直剪试验过程中，施加法向荷载至预定值并保持常值，逐级增加剪力，测量相应位移。本实验依次施加0.2，0.4，0.6 和0.8 MPa法向荷载，分别测量相应位移，根据测量结果绘制节理剪切应力-位移曲线。取其中 1组节理剪切应力-位移曲线，如图3所示。

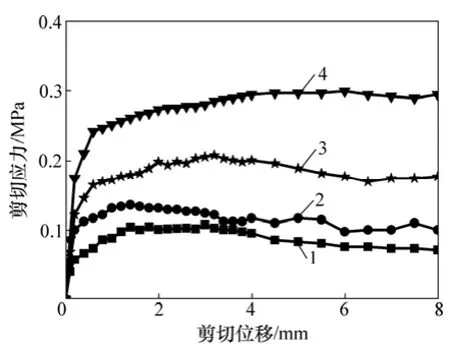
图3　节理直剪试验剪切应力-位移曲线Fig. 3　Shear stress-displacement curves of joint from direct shear test

2.2持续屈服节理模型力学参数确定方法

持续屈服节理模型力学参数包括节理切向刚度系数及其指数、节理法向刚度系数及其指数、节理初始摩擦角、基本摩擦角以及节理粗糙度等力学参数。

2.2.1节理刚度参数

在常法向应力下，节理剪切试验主要分为2步：1） 施加法向荷载至预定值；2） 施加水平荷载直至节理面滑动达到预定剪切位移。节理法向刚度表征步骤1）中节理抵抗法向变形的能力；节理剪切刚度表征步骤2）中节理抵抗剪切变形的能力。在常法向应力下，节理剪切试验中，节理法向刚度对剪切应力-位移曲线没有影响，下面重点介绍节理切向刚度的获取方法。

1） 节理切向刚度。节理切向刚度为节理在剪切应力作用下抵抗剪切变形的能力，可以从节理剪切试验结果中获取。因节理表面凹凸不平，几乎在剪切实验开始就伴随着节理面微凸体的磨损破坏，且实验数据为离散数据，较难直接从剪切应力-位移曲线获取准确的节理刚度。本文根据KULHAWAY［6］提出的表征剪切应力-位移曲线的双曲线方程式

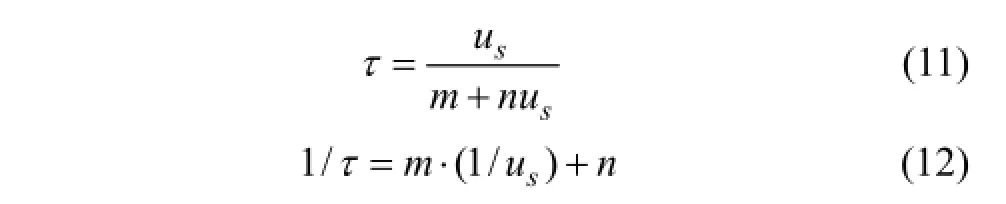
并结合试验数据，拟合1/τ-1/us曲线，确定 m，进而确定节理切向刚度。式中：τ为剪切应力；us为剪切位移；m和n为常数，m=1/ks，n=1/τult；τult为双曲线水平渐近值。

图4所示为根据本文砂岩岩芯节理直剪试验剪切应力峰值前数据拟合的 1/τ-1/us曲线。由拟合方程得出对应法向应力0.2，0.4，0.6和0.8 MPa时m分别为1.57，1.25，0.97和0.72 mm/MPa，进而由ks=1/m求得ks分别为0.64，0.80，1.00和1.32 MPa/mm。

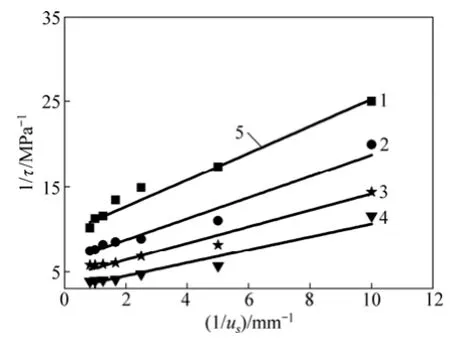
图4　节理1/τ-1/us拟合曲线Fig. 4　1/τ-1/usfitting curves of joint

节理剪切试验结果表明：节理剪切刚度和法向应力之间为非线性曲线关系，KULHAWAY等［6-7］采用指数方程可较好地拟合此关系曲线。图5所示为节理剪切刚度ks和法向应力σn的指数拟合曲线，其拟合方程为

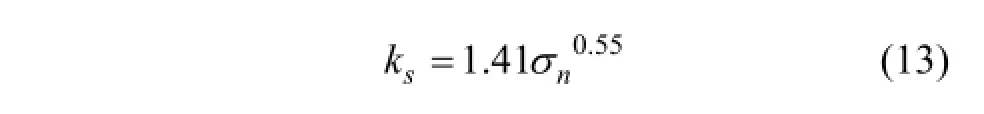
从式（13）可知：节理切向刚度系数as为1.41，切向刚度指数es为0.55。

2） 节理法向刚度。节理法向刚度是节理在法向应力作用下抵抗法向变形的能力，由节理法向应力-位移曲线确定。法向应力与法向位移关系的拟合方程可表示为

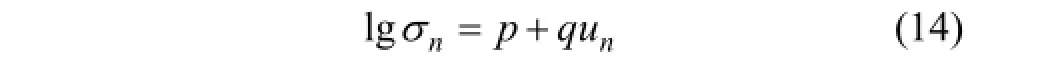
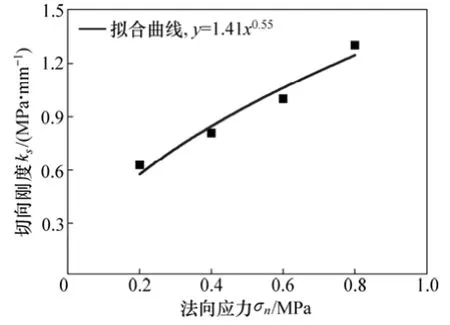
图5　节理剪切刚度-法向应力拟合曲线Fig. 5　Shear stiffness-normal stress fitting curve of joint

由此得法向刚度表达式为

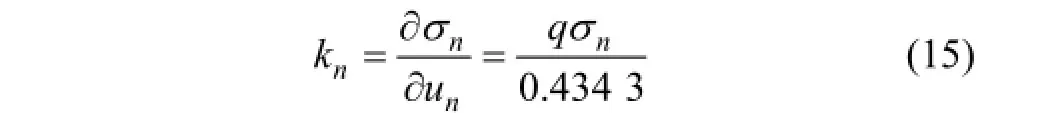
根据节理法向加载试验法向应力与法向位移关系，拟合lgσn-un曲线，得节理法向刚度表达式为

式中：p和q分别为lgσn-un拟合曲线的截距和斜率。从式（16）可知法向刚度系数an为14.48，法向刚度指数en为1.00。

2.2.2节理摩擦角参数

持续屈服节理模型力学参数中的节理摩擦角包括节理初始摩擦角和节理基本摩擦角φ。

基本摩擦角φ由节理磨光面剪切试验残余摩擦角确定。磨光面剪切试验是将试样的不连续面磨光后进行试验，试验过程及试验结果与节理面直剪试验的相同。

2.2.3节理粗糙度参数

节理粗糙度的表征是一个复杂问题。BARTON［4］采用粗糙度因子 JRC来表征节理面的粗糙度，由此确定的节理剪切强度公式为

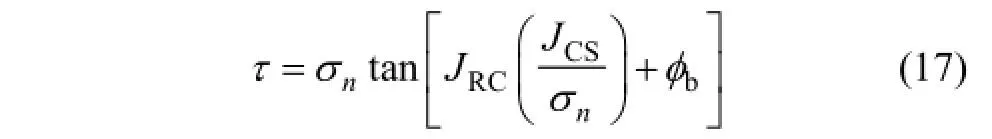
式中：JRC为节理面粗糙度因子；JCS为节理面的抗压强度； φb为节理面基本摩擦角。JRC常采用对照 JRC典型剖面目测确定。

在持续屈服节理模型中，节理面剪切强度的计算公式为式（6）和式（7）。节理面粗糙度参数R采用具有一维长度单位的节理面凸起高度幅值来表征。文献［7］用JRA表示节理面凸起高度幅值，即本文中的R，并且给出了不同风化程度砂岩 JRA范围。文献［25］根据BARTON［4］绘制的 JRC估算和尺寸效应图表得到拟合方程（18）。JRC和JRA关系式为

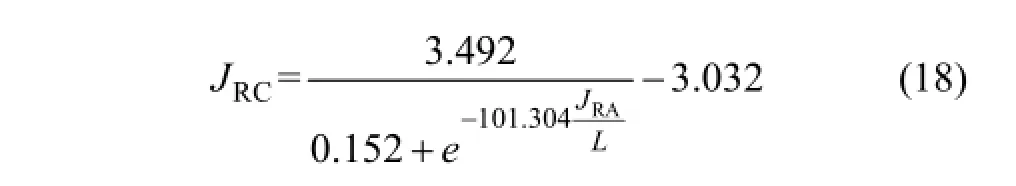
式中：JRA为节理面凸起高度幅值；L为与典型JRC剖面对比时节理剖面长度。本文采用式（18）计算并经测量检验，确定该组试件节理面粗糙度R为0.003 5 m。

2.3数值试验

2.3.1试验模型

采用块体离散元软件3DEC，建立含1个水平节理面、直径×高为60 mm×120 mm的圆柱形砂岩芯数值试验模型，该模型及模型边界条件如图 6所示。图 6中：σn为法向应力；v为切向加载速度，v=0.005 m/s。

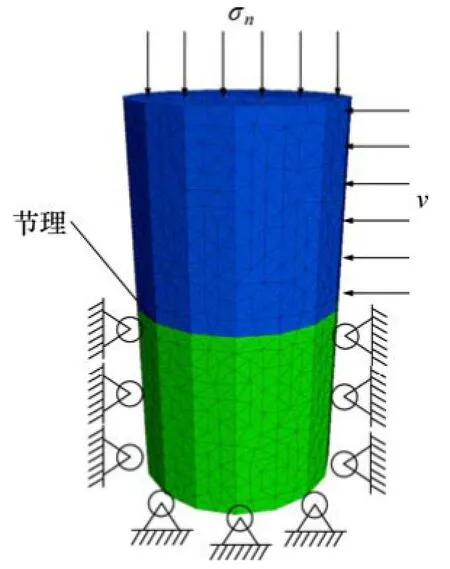
图6　数值试验模型Fig. 6　Numerical experiment model

2.3.2数值模型力学参数

数值模型包括岩石块体和节理2部分。岩石块体采用弹性、各向同性模型模拟，其力学参数通过岩石单轴压缩等室内试验确定，见表 1。节理采用持续屈服节理模型模拟，其力学参数见表2。

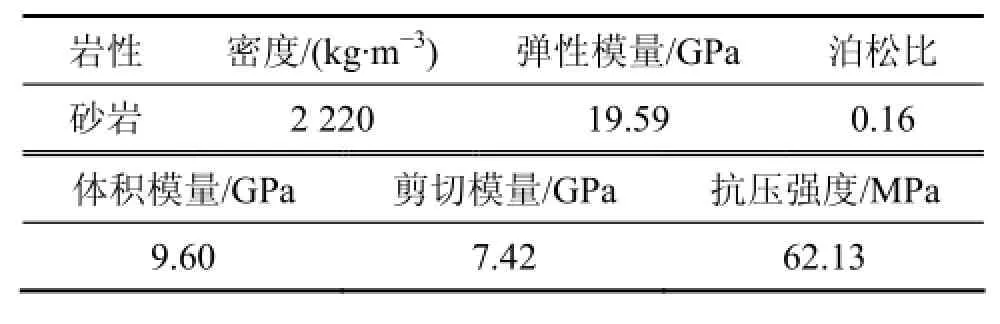
表1　岩石力学参数Table 1 Mechanics parameters of rock

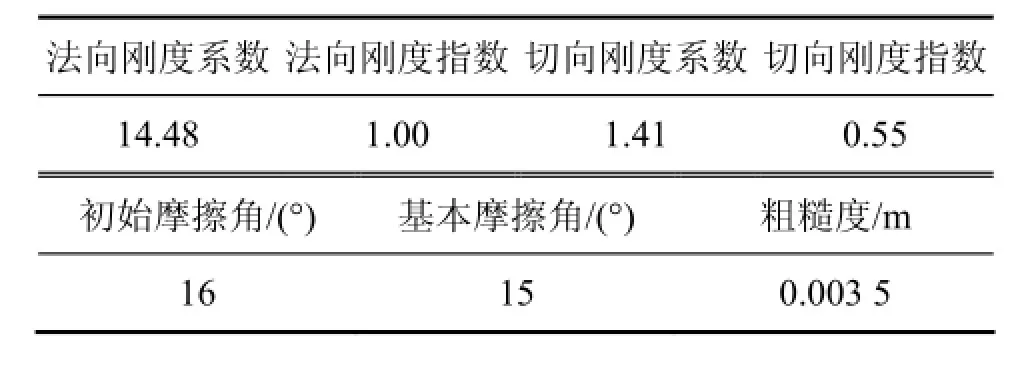
表2　持续屈服节理模型力学参数Table 2 Mechanics parameters of continuously yielding joint model

3　试验结果分析、对比及参数影响研究

3.1数值试验剪切应力-位移曲线

图7所示为节理数值试验中剪切应力-位移曲线。图7表明：节理剪切应力随剪切位移变化分为4个阶段，即曲线上升阶段—峰值阶段—软化阶段—残余应力阶段；在曲线上升阶段，节理面的切向刚度随节理位移增加逐渐非线性降低，剪切应力-位移曲线表现出双曲线特征；节理面达到峰值强度后进入软化阶段。由于本文实验中砂岩的节理初始摩擦角与节理基本摩擦角接近，因此，软化阶段曲线下降十分缓慢；剪切应力最后达到残余应力。

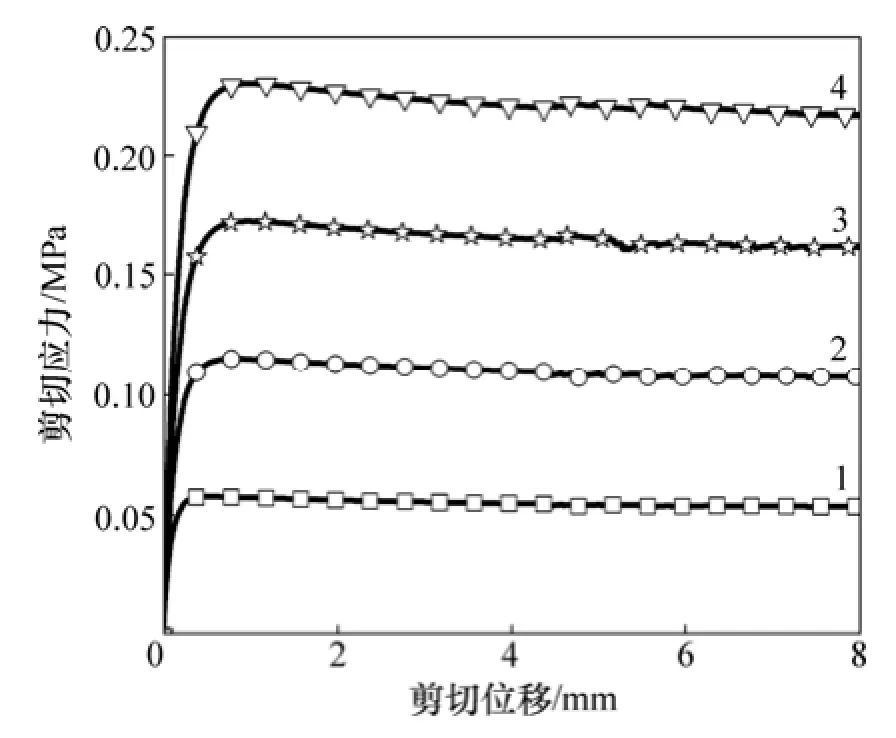
图7　节理数值直剪试验剪切应力-位移曲线Fig. 7　Shear stress-displacement curves of joint from numerical experiment

3.2节理面子接触及剪切应力

在节理数值计算模型中，节理面作为2个块体间的接触面，由多个子接触构成。剪切之初，同一几何位置处的上、下2个子接触点重合，随着剪切位移增加，2点逐渐滑移。在法向应力为0.4 MPa的数值剪切试验过程中，对应剪切曲线不同阶段的4种剪切位移（曲线上升阶段0.11 mm、峰值阶段0.40 mm、软化阶段2.30 mm、残余应力阶段7.30 mm），节理面子接触滑移及其相应的剪切应力云图如图8所示。从图8可见：当剪切位移很小时，子接触2点重合（见图8（a）），相应剪切应力较小（见图 8（b））；随剪切位移增加，剪切应力增大，子接触2点分离（见图8（c），节理破坏，剪切应力达到峰值（见图8（d））；峰值后子接触逐渐滑移（见图8（e）），节理面发生变形（见图8（g）），剪切应力逐渐在节理面Y方向两端应力集中（见图8（f）和图8（h）），最终节理面达到残余强度（见图8（h）。

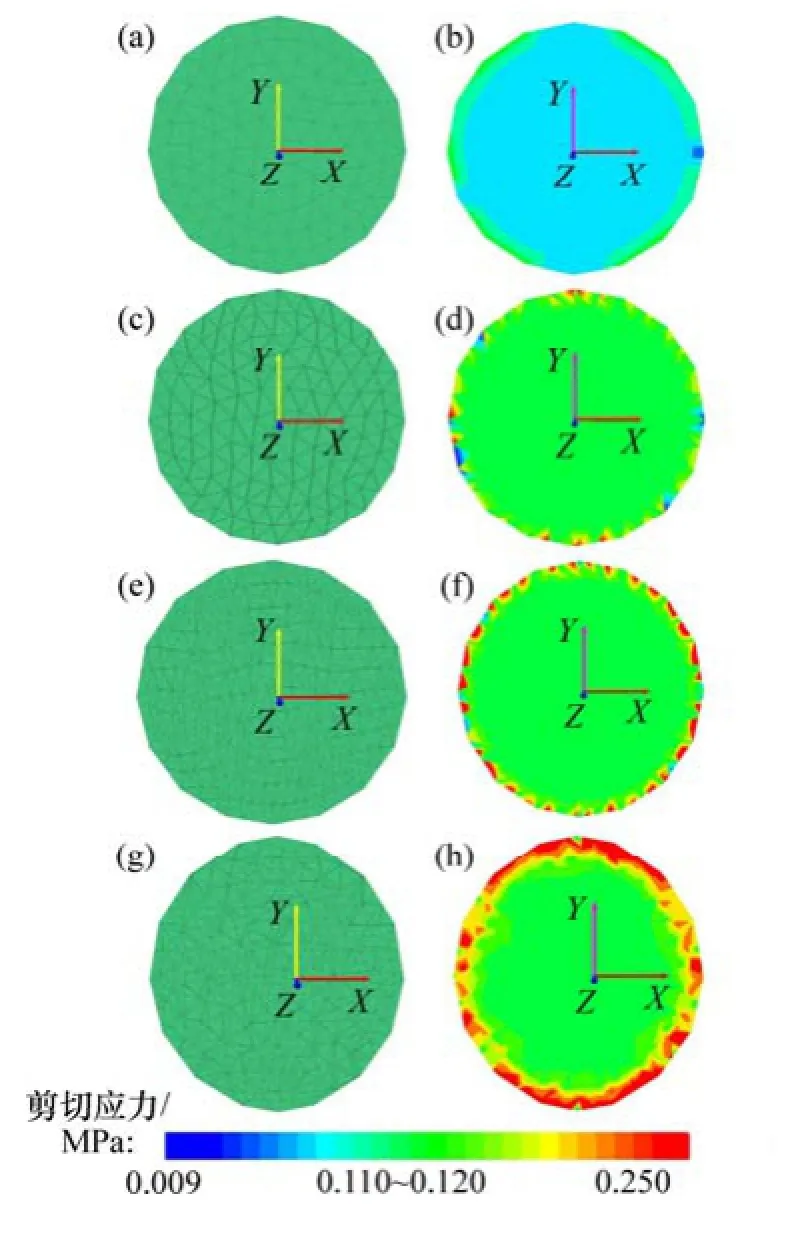
图8　节理面子接触滑移及剪切应力变化Fig. 8　Subcontact sliding of joint and change of shear stress

3.3数值和室内试验结果对比

图 9所示为数值及室内节理直剪试验的剪切应力-位移对比曲线。其中，图9（a）所示为节理剪切全过程试验结果对比。为清晰表示剪切初期试验结果对比，将图9（a）中剪切位移0～1 mm之间曲线表示在图9（b）中。图9表明：

1） 剪切峰值强度前，随着剪切位移增加，数值和室内剪切试验中节理剪切应力曲线均上升，表明节理从开始剪切时就存在损伤，伴随着少量塑性变形；随损伤累积，塑性变形增大，剪切强度达到峰值强度；在剪切峰值强度前，数值试验曲线和剪切试验曲线吻合较好，尤其是在峰值强度时两者趋于一致，表明持续屈服节理本构模型可较好地反映节理剪切峰值强度及之前的切向变形。

2） 剪切峰值强度后，室内试验曲线出现了强度硬化—强度软化—残余强度3个阶段；数值试验曲线出现了强度软化—残余强度2个阶段。二者出现偏差，但除0.8 MPa试验曲线较晚进入残余强度阶段外，其余3条曲线室内与数值试验残余强度趋于一致。

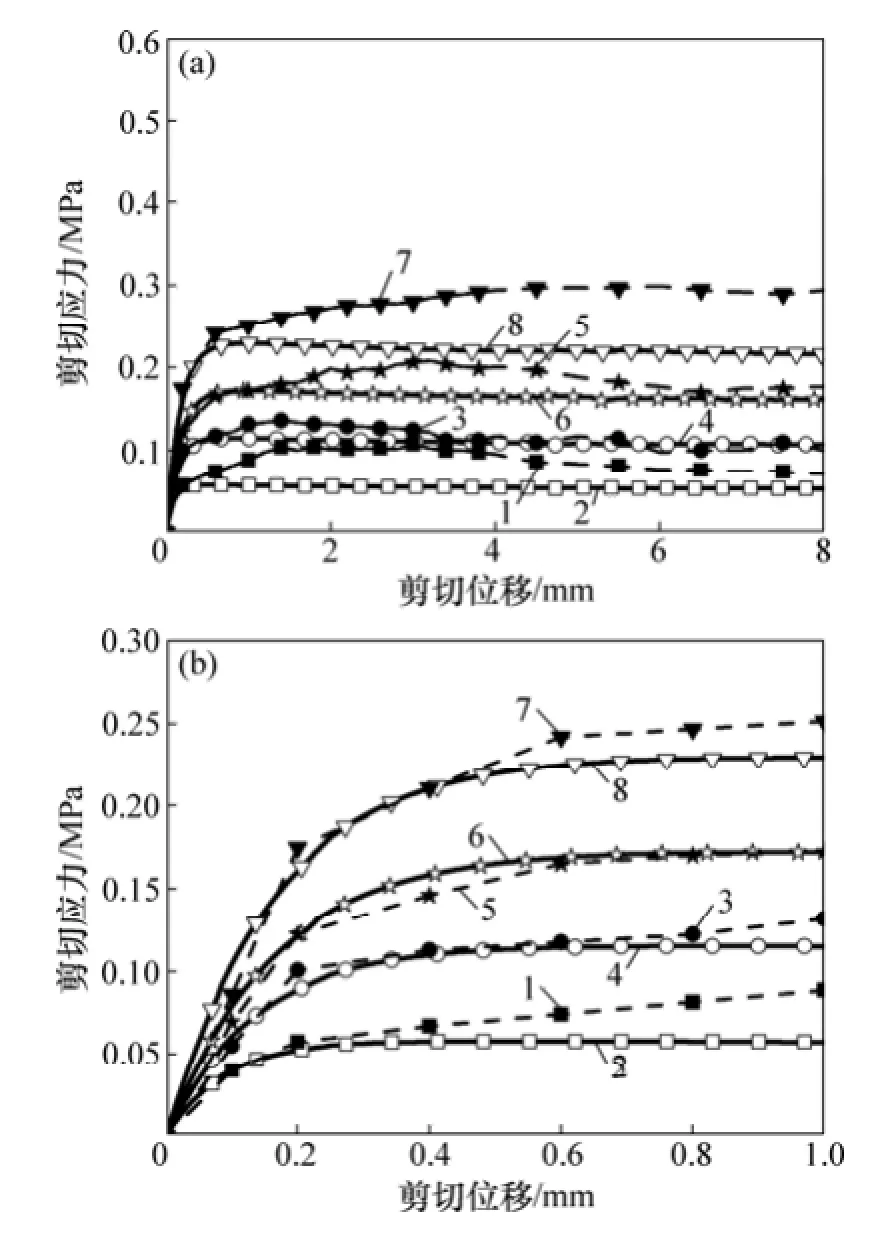
图9　节理数值与室内直剪试验结果对比曲线Fig. 9　Comparison of shear stress-displacement curves between indoor test and numerical experiment of joint

室内试验出现剪切强度硬化现象，其主要原因是：节理面凸起岩石颗粒分布不均匀，不规则，在剪切过程中凸台被剪断、碾碎，产生磨损破坏。此磨损破坏过程是极为复杂的物理过程，碾碎的凸体颗粒充填在接触面的凹槽内部，逐渐堆积，甚至有时会卡在凹槽处，导致剪切强度上升，出现强度硬化现象。

3.4参数影响规律

3.4.1粗糙度对节理剪切强度的影响规律

粗糙度是节理面重要力学参数之一，影响节理剪切强度。以法向应力0.4 MPa为例，在其他力学参数相同时，研究不同粗糙度对节理剪切强度的影响。图10（a）所示为不同粗糙度时剪切应力-位移曲线，图10（b）所示为粗糙度与节理剪切强度的拟合曲线。图10表明：

1） 在切向刚度相同条件下，粗糙度对剪切应力的影响主要集中在峰值强度—应变软化—残余强度阶段。

2） 随粗糙度增加，剪切峰值强度按幂函数式（19）增大，针对本例拟合方程为式（20）。

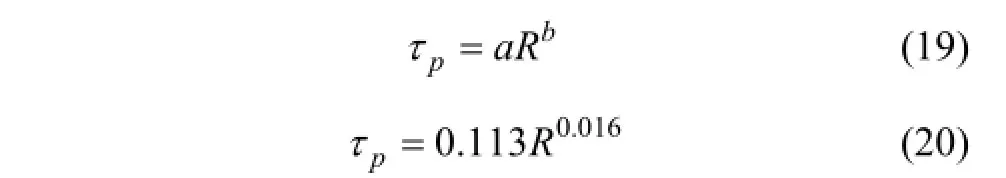
式中：τp为剪切峰值强度；R为粗糙度；a和b为拟合参数。

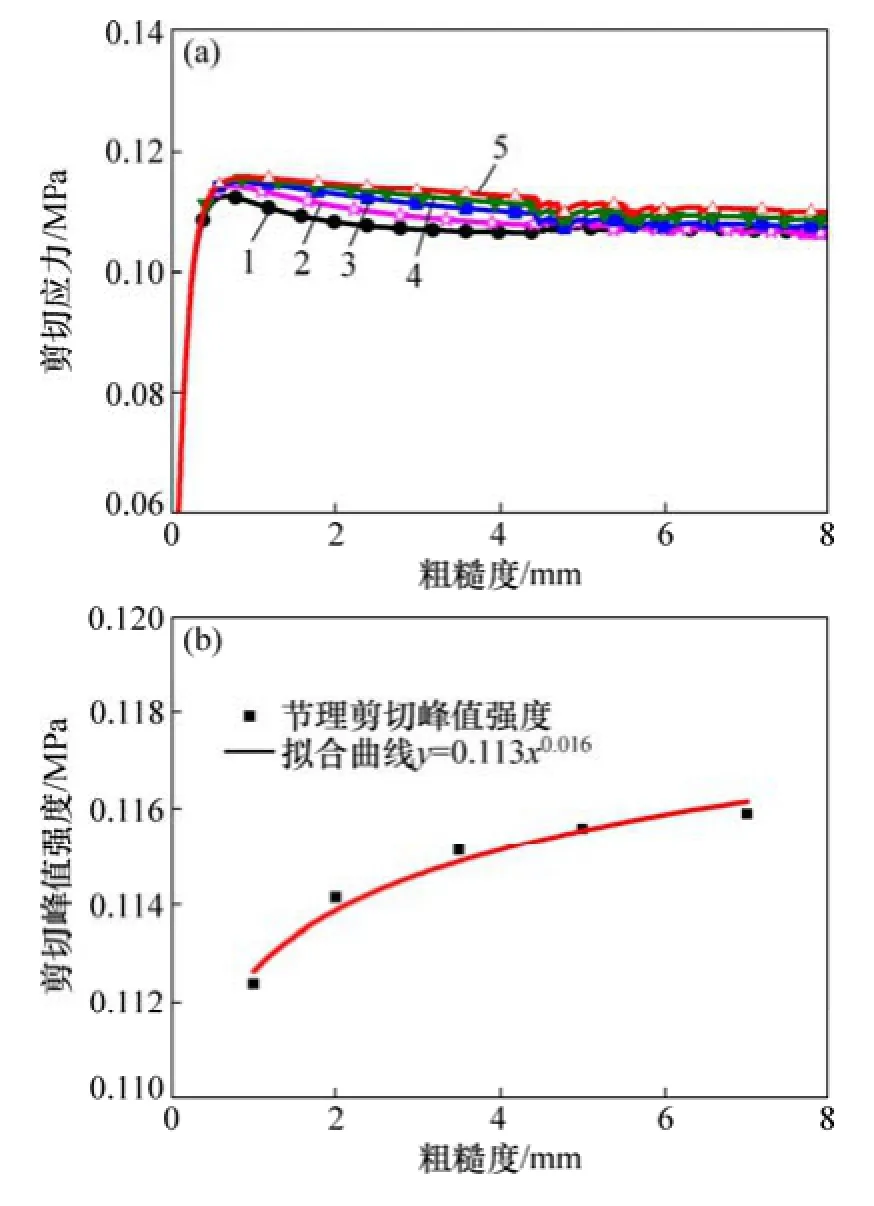
图10　节理粗糙度对剪切强度的影响Fig. 10 Effect of joints roughness on shear strength

3） 在应变软化阶段，随粗糙度增加，剪切应力-剪切位移曲线下降速度变缓慢。

4） 在残余强度阶段，随粗糙度增加，节理残余强度增大。

3.4.2初始摩擦角与基本摩擦角差值对节理剪切强度的影响规律

初始摩擦角与基本摩擦角差值显著影响节理剪切峰值强度及剪切应变软化。以法向应力0.4 MPa为例，在其他力学参数相同条件下，研究节理初始摩擦角不同取值（16°，20°，25°，30°，35°和40°）与基本摩擦角φ=15°的差值对节理剪切强度的影响。

图11（a）所示为节理不同摩擦角差值下剪切应力-位移曲线，图11（b）所示为该差值与剪切峰值强度的拟合曲线。图11表明：

1） 随初始摩擦角与基本摩擦角差值增大，节理剪切强度按式（21）呈线性增大，针对本例，拟合方程为式（22）。

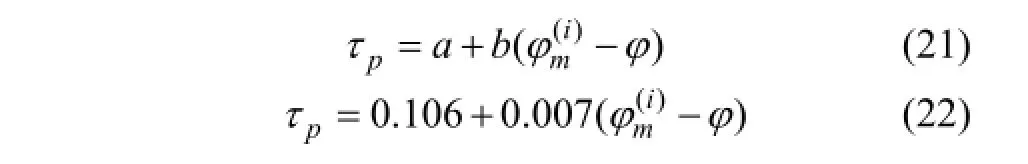
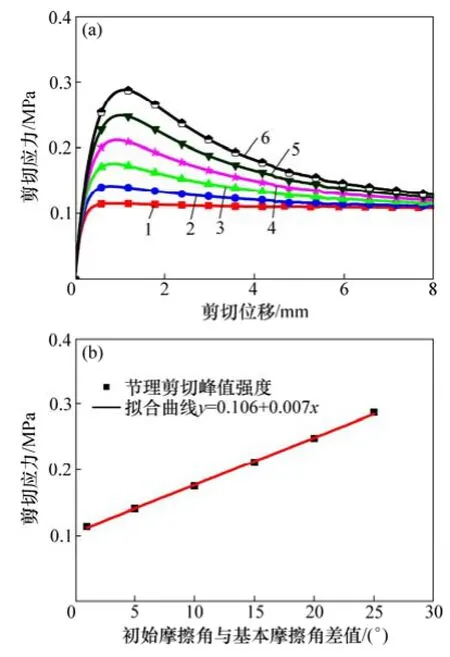
图11　节理初始摩擦角与基本摩擦角差值对剪切强度的影响Fig. 11 Effect of initial friction angle and basic friction of joint on shear strength

式中：a和b分别为线性拟合的截距和斜率。

2） 随初始摩擦角与基本摩擦角差值增大，节理残余强度增大，但增大幅度远小于剪切峰值强度增大幅度，因此，曲线应变软化阶段坡度变大。

4　结论

1） 由于节理面直剪试验开始就伴随着节理面微凸体的磨损破坏以及试验结果数据的离散性，故难以直接确定节理剪切刚度。本文通过试验数据拟合求得节理刚度系数和刚度指数，不失为一种有效的方法。

2） 持续屈服节理模型可以实现节理刚度随法向应力、塑性位移累积而变化。法向应力越大，节理刚度越大；当法向应力不变时，节理剪切刚度随节理塑性位移累积而减小。

3） 基于持续屈服节理本构模型，节理剪切应力随剪切位移的变化分4个阶段，即曲线上升阶段—峰值阶段—软化阶段—残余应力阶段。

4） 持续屈服节理本构模型能较好地反映节理剪切峰值强度及峰值强度前剪切应力与剪切变形的非线性关系，且能较好地反映峰值强度后节理应变软化及残余强度等节理力学性质。

5） 持续屈服节理本构模型引入了节理面粗糙度参数。在切向刚度相同的条件下，粗糙度对剪切应力的影响主要集中在峰值强度—应变软化—残余强度阶段。随粗糙度增大，剪切峰值强度按幂函数增大，应变软化阶段剪切应力-剪切位移曲线下降变缓慢，节理残余强度增大。

6） 节理剪切峰值强度与初始摩擦角、基本摩擦角的差值线性相关；随摩擦角差值增大，节理剪切峰值强度及残余强度均增大，但剪切峰值强度增大幅度远大于残余强度增大幅度，因此，剪切应力-位移曲线应变软化阶段坡度变大。

［1］ 蔡美峰， 何满潮， 刘冬燕. 岩石力学与工程［M］. 北京： 科学出版社， 2002： 75-95. CAI Meifeng， HE Manchao， LIU Dongyan. Rock mechanics and engineering［M］. Beijing： Science Press， 2002： 75-95.

［2］ GOODMAN R E， TAYLOR R L， BREKKE T. A model for the mechanics of jointed rock［J］. J Soil Mech Fdns： Div Proc Am Soc Civ Engrs， 1968， 94（SM3）： 637-659.

［3］ GOODMAN R E. The mechanical properties of joints［C］//Proc 3rd Congr ISRM. Denver， 1974， IA： 127-140.

［4］ BARTON N. Review of a new shear strength criterion for rock joints［J］. Engineering Geology， 1973， 7（4）： 287-332.

［5］ BARTON N， CHOUBEY V. The shear strength of rock joints in theory and practice［J］. Rock Mechanics and Rock Engineering，1977， 10（1）： 1-54.

［6］ KULHAWAY F H. Stress-deformation properties of rock and rock discontinuities［J］. Engineering Geology， 1975， 9（4）：327-350.

［7］ BANDIS S C， LUMSDEN A C， BARTON N R. Fundamentals of rock joint deformation［J］. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts，1983， 20（6）： 249-268.

［8］ 赵坚. 岩石节理吻合系数及其对节理特性的影响［J］. 岩石力学与工程学报， 1997， 16（6）： 514-521. ZHAO Jian. Joint matching coefficient and effects to behaviour of rock joint［J］. Chinese Journal of Rock Mechanics and Engineering， 1997， 16（6）： 514-521.

［9］ 杜时贵， 胡晓飞， 郭霄， 等. JRC-JCS模型与直剪试验对比研究［J］. 岩石力学与工程学报， 2008， 27（增1）： 2747-2753. DU Shigui， HU Xiaofei， GUO Xiao， et al. Comparison study of JRC-JCS model and direct shear test［J］. Chinese Journal of Rock Mechanics and Engineering， 2008， 27（Supp.1）： 2747-2753.

［10］ 杜时贵， 胡晓飞， 罗战友， 等. 节理抗剪强度综合评价的试验研究［J］. 工程地质学报， 2008， 16（1）： 89-97. DU Shigui， HU Xiaofei， LUO Zhanyou， et al. A comprehensive experimental evaluation of rock joint shear strength［J］. Chinese Journal of Engineering Geology， 2008， 16（1）： 89-97.

［11］ MAKURAT A， AHOLA M， KHAIR K， et al. The DECOVALEX test-case one［J］. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts， 1995， 32（5）：399-408.

［12］ HOMAND F， BELEM T， SOULEY M. Friction and degradation of rock joint surfaces under shear loads［J］. International Journal for Numerical and Analytical Methods in Geomechanics， 2001，25（10）： 973-999.

［13］ 朱小明， 李海波， 刘博， 等. 含二阶起伏体的模拟岩体节理试样剪切特性试验研究［J］. 岩土力学， 2012， 33（2）： 354-360. ZHU Xiaoming， LI Haibo， LIU Bo， et al. Experimental study of shear characteristics by simulating rock mass joints sample with second-order asperities［J］. Rock and Soil Mechanics， 2012，33（2）： 354-360.

［14］ MIRZAGHORBANALI A， NEMCIK J， AZIZ N. Effects of shear rate on cyclic loading shear behaviour of rock joints under constant normal stiffness conditions［J］. Rock Mechanics and Rock Engineering， 2014， 47（5）： 1931-1938.

［15］ MIRZAGHORBANALI A， NEMCIK J， AZIZ N. Effects of cyclic loading on the shear behaviour of in filled rock joints under constant normal stiffness conditions［J］. Rock Mechanics and Rock Engineering， 2014， 47（4）： 1373-1391.

［16］ 夏才初， 宋英龙， 唐志成， 等. 反复直剪试验节理强度与粗糙度变化的研究［J］. 中南大学学报（自然科学版）， 2012， 43（9）：3589-3594. XIA Caichu， SONG Yinglong， TANG Zhicheng， et al. Shear strength and morphology characteristic evolution of joint surface under cyclic loads［J］. Journal of Central South University （Science and Technology）， 2012， 43（9）： 3589-3594.

［17］ 吴顺川， 高艳华， 高永涛， 等. 等效节理岩体表征单元体研究［J］. 中国矿业大学学报， 2014， 43（6）： 1120-1126. WU Sunchuan， GAO Yanhua， GAO Yongtao， et al. Research on representative elemental volume of equivalent joint rock mass［J］. Journal of China University of Mining & Technology， 2014，43（6）： 1120-1126.

［18］ 王贺， 高永涛， 金爱兵， 等. 节理岩体刚度参数选取与三维离散元模拟［J］. 岩石力学与工程学报， 2014， 33（增 1）：2894-2900. WANG He， GAO Yongtao， JIN Aibing， et al. Determination of stiffness parameters of jointed rock masses with 3DEC simulations［J］. Chinese Journal of Rock Mechanics and Engineering， 2014， 33（Suppl 1）： 2894-2900.

［19］ CUNDALL P A， HART R D. Analysis of block test no. 1 inelastic rock mass behavior： phase 2-a characterization of joint behavior （final report）［R］. Itasca Conculting Group， Rockwell Hanford Operations， 1984： Subcontract SA-957.

［20］ 肖卫国， 兑关锁， 陈铁林， 等. 剪胀和破坏耦合的节理岩体本构模型的研究［J］. 岩石力学与工程学报， 2009， 28（12）：2535-2543. XIAO Weiguo， DUI Guansuo， CHEN Tielin， et al. A study of constitutive model coupling dilatancy and degradation for jointed rock［J］. Chinese Journal of Rock Mechanics and Engineering， 2009， 28（12）： 2535-2543.

［21］ 唐志成， 夏才初， 肖素光. 节理剪切应力-位移本构模型及剪胀现象分析［J］. 岩石力学与工程学报， 2011， 30（5）： 917-925. TANG Zhicheng， XIA Caichu， XIAO Suguang. Constitutive model for joint shear stress-displacement and analysis of dilation［J］. Chinese Journal of Rock Mechanics and Engineering，2011， 30（5）： 917-925.

［22］ CUNDALL P A， LEMOS J V. Numerical simulation of fault instabilities with a continuously yielding joint model［C］//FAIRHURST C， ed. Rock bursts and Seismicity in Mines. Rotterdam： A A Balkema， 1990： 147-152.

［23］ MA Mingjun， BRADY B H. Analysis of the dynamic performance of an underground excavation in jointed rock under repeated seismic loading［J］. Geotechnical and Geological Engineering， 1999， 17（1）： 1-20.

［24］ Itasca Consulting Group. 3DEC （3 dimensional distinct element code） theory and background［M］. Itasca： Itasca Consulting Group， 2007， Theory and Background 3： 1-5.

［25］ ZHANG Guangcheng， KARAKUS M， TANG Huiming， et al. A new method estimating the 2D joint roughness coefficient for discontinuity surfaces in rock masses［J］. International Journal of Rock Mechanics & Mining Sciences， 2014， 72： 191-198.

（编辑 陈灿华）

Numerical simulation of joint direct shear test based on continuously yielding joint model

GAO Yanhua1， WU Shunchuan1， WANG He2， XIAO Shu3

（1. School of Civil & Environmental Engineering， University of Science and Technology Beijing， Beijing 100083， China；2. Beijing General Research Institute of Mining and Metallurgy， Beijing 100070， China；3. Three Gorges Geotechnical Consultants Co.，Ltd， Wuhan 430074， China）

According to laboratory experiments of standstone from Pingshuo open-pit coal mine in Shanxi Province， the mechanical parameters of rock and joint were determined. Based on continuously yielding joint model， joint direct shear numerical test was conducted by using FISH programs embedded within 3DEC software. The effects of joint roughness，the difference between initial friction angle and basic friction angle on the shear strength were studied. The results show that shear stress-displacement curves of joint obtained from numerical experiments can reflect four stages of joint shearing stress， i.e. increasing—peak—strain softening—residual strength. Compared with the results of indoor test，continuously yielding joint model incorporates irreversible non-linear behaviour from the onset of shear loading， and can effectively reflect the mechanical behaviour of joint strain-softening and residual strength after peak strength. With the increase of roughness， shear strength of joint increases with the power function， and it increases with the increase of the friction angle difference.

continuously yielding joint model； joint normal stiffness； joint shear stiffness； roughness； friction angle；direct shear test

TU45

A

1672-7207（2016）04-1253-09

10.11817/j.issn.1672-7207.2016.04.023

2015-06-11；

2015-07-20

国家自然科学基金资助项目（51074014，51174014）；科技北京百名领军人才培养工程项目（Z151100000315014）；中国博士后科学基金资助项目（2015M570037）（Projects （51074014， 51174014） supported by the National Natural Science Foundation of China；Project （Z151100000315014） supported by Beijing Training Project for the Leading Talents in Science and Technology； Project （2015M570037）supported by China Postdoctoral Science Foundation of China）

吴顺川，博士，教授，博士生导师，从事岩土工程、采矿工程等研究；E-mail：wushunchuan@ustb.edu.cn