适用于多种物料的圆锥破碎机腔型时变磨损预测
马彦军,范秀敏,何其昌
(上海交通大学 机械与动力工程学院,机械系统与振动国家重点实验室,上海,200240)
适用于多种物料的圆锥破碎机腔型时变磨损预测
马彦军,范秀敏,何其昌
(上海交通大学 机械与动力工程学院,机械系统与振动国家重点实验室,上海,200240)
为动态分析计算圆锥破碎机物料质量以支持产品的优化设计,利用 RMT-150B岩石力学实验系统对圆锥破碎机层压破碎过程进行模拟实验,以此建立1个基于物料抗压强度、压缩比和粒度分布系数的多种物料破碎力求解模型。基于层压破碎理论和物料运动学特性,并结合物料破碎生产线的圆锥破碎机腔型磨损量,得到关于破碎腔表面磨损的时变磨损模型。采集分析破碎腔磨损的实验结果,并与时变磨损模型的求解结果进行对比分析。研究结果表明:利用所建立的时变磨损模型可以对破碎腔磨损量进行求解,其求解结果与实验结果相符,可实现生产线中对圆锥破碎机腔型表面磨损量的预测。
圆锥破碎机;破碎力;磨损;粒度分布;破碎流程
圆锥破碎机广泛地用于矿山、水利、冶炼和建筑等工业部门,是脆性物料中细碎的主要设备。在其工作过程中,破碎壁随着动锥围绕破碎轴线作偏心运动,物料在破碎腔内受到挤压而破碎成小颗粒产品,破碎腔内物料挤压破碎使得破碎壁表面承受相应的破碎力,随着工作时间的增加,不可避免地导致破碎腔的磨损量越来越大,其破碎产品的产量、粒度分布和针片率将出现较大改变,大大降低了圆锥破碎机的性能[1-4],因此,需要研究圆锥破碎机的物料破碎力和破碎腔磨损模型,以对圆锥破碎机工作过程中的磨损进行补偿,提高其工作性能。在实际工程应用中,圆锥破碎机会对各种不同的抗压强度物料进行破碎,其产生的挤压破碎力也不相同,并且物料会磨损圆锥破碎机整个破碎腔,而破碎腔的磨损将对破碎产品质量产生较大的影响,因此,从理论上研究多种物料破碎力模型和时变磨损模型十分重要。LINDQVIS等[5-6]提出圆锥破碎机的破碎腔的磨损量与最大破碎力成正比。LINDQVIST等[7]经研究认为挤压破碎力的特性与物料挤压破碎过程中的压缩比和物料颗粒的粒度分布系数相关。LINDQVIST等[8]提出了压缩比和每个破碎层破碎力分布角度的计算方法。董钢等[9-12]建立了较精确的单种物料破碎力模型。然而,破碎现场的矿石种类繁多,单种物料模型不能够满足理论计算的需求,因此,对多物料破碎力模型和圆锥破碎机破碎腔的时变磨损模型进行系统研究有重要意义。鉴于此,本文作者设计并进行多种物料的挤压破碎力实验,利用RMT-150B岩石力学实验系统模拟不同物料在圆锥破碎机中的层压破碎过程,并以此建立较精确的多种物料破碎力模型,并在此基础上建立适用于多种物料的破碎腔时变磨损模型,从而为实际生产过程中圆锥破碎机排料口的磨损补偿提供依据。
1 适用于多种物料的破碎力建模
1.1实验装置和材料
物料挤压破碎设备为 RMT-150B岩石力学实验系统,利用该系统对散体物料进行挤压破碎,该过程的应力应变可以通过传感器测定,并可以得到载荷位移关系图和应力应变关系图。图1所示为压缩比定义简图,层压破碎实验前的散体物料高度为 b,对物料施加压力p,进给压缩量s,石子压碎仪内的散体物料发生层压破碎,施加不同位移以实现不同压缩比的实验工况,之后利用新型标准筛对层压破碎的破碎产品进行筛分分析,得到一系列的破碎产品粒度。

图1 压缩比定义简图Fig. 1 Diagram of compression ratio
实验散体物料为四川成都某矿业股份有限公司提供的玄武岩矿石、花岗岩矿石和来自内蒙包头某采石场的铁矿石,另外是来自江苏镇江的石灰石矿石。岩石物料由鄂式破碎机破碎得到。对散体物料进行筛分和挤压破碎后再次筛分,将散体物料粒度分为9.5~16.0,16.0~19.0,19.0~26.5,26.5~31.5 mm共 4个粒级范围,每种散体物料的总质量约为150 kg,作为挤压破碎实验的散体物料。并对每种散体物料的抗压强度进行测定,依据岩石抗压强度测试的相关标准,切割成长×宽×高为5 cm×5 cm×5 cm的标准试样。将试样放置在RMT-150B实验平台上,并进行缓慢加载,直至物料样本发生破坏,记录最大载荷,物料的抗压强度测试结果见表1。
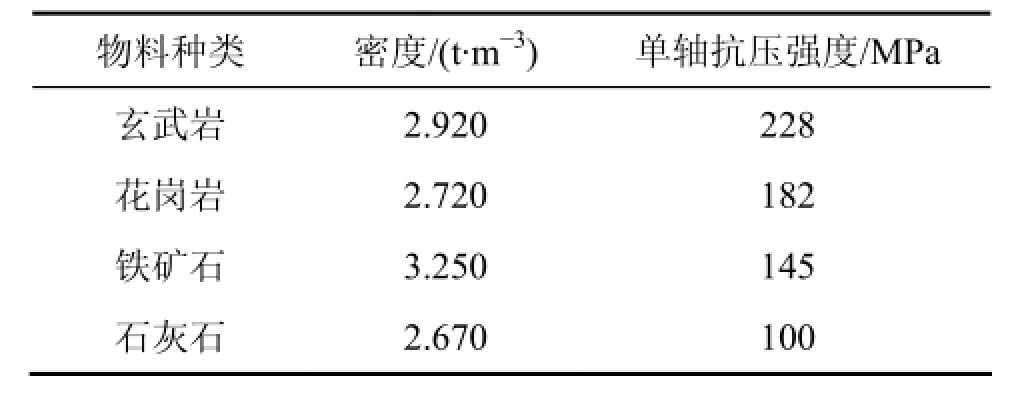
表1 物料的单轴抗压强度测试结果Table 1 Experimental results of rock material uniaxial compressive strength
1.2实验方案
挤压破碎力与层压破碎过程中的压缩比、物料的粒度分布系数和物料的抗压强度系数有关[13-15]。压缩比反映物料受到的压缩程度,可由式(1)计算得到;粒度分布系数反映物料颗粒粒径分布情况,可以通过式(2)和式(3)计算得到。
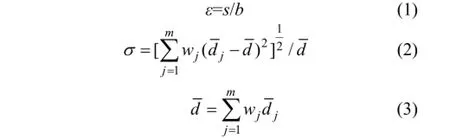
式中:ε为压缩比,表示物料受到压缩的程度,压缩比越大,说明物料的体积被压缩得越大;σ为粒度分布系数;wj为粒级j内散体物料所占质量分数;为粒级j内散体物料的平均粒度为各粒级平均粒度。基于对层压破碎过程相关影响参数的分析和研究,选取物料粒度分布系数、压缩比和抗压强度作为主要实验参数,基于破碎装备工作过程中参数的大致范围,选取实验水平值,并进行实验设计。利用RMT-150B岩石力学实验系统对石子压碎仪中的散体物料进行层压破碎实验,模拟圆锥破碎机破碎腔中各破碎层散体物料的层压破碎过程,从而得到一系列挤压破碎力的实验结果。实验流程如图2所示,将散体物料放入石子压碎仪中并对压柱施加压力FN,破碎实验中的进给量分别为s1,s2,…,sN,并利用标准筛进行筛分,从而利用一系列层压破碎实验模拟圆锥破碎机整个破碎腔对物料的层压破碎过程,记录实验数据并对破碎成品进行筛分,得到实验结果如表2所示。

图2 散体物料挤压破碎实验流程Fig. 2 Experimental processes of rock material interpartical breakage
1.3破碎力数学模型
基于物料的层压破碎实验参数,采用多项式拟合分析各个参数对破碎力的影响,其中压缩比对挤压破碎力的影响如图3所示。
在层压破碎实验中,4种物料的破碎力均随着压缩比的增大而增大。比较图3中的轴向应力拟合曲线可见:在压缩比一定时,散体物料为玄武岩时所受的挤压破碎力最大,其次是花岗岩、铁矿石和石灰石。在常用的矿石物料中,花岗长英岩的抗压强度最高,为350 MPa,现用物料的抗压系数表示物料抗压特性,用于破碎力模型建模。

式中:K为物料的抗压强度;λ为物料的抗压系数。基于获得的实验数据,观察抗压系数、粒度分布系数和压缩比对破碎力的影响,然后作出各个参数和物料破碎力的散点图,得出预测多物料破碎力的数学模型。由于这些参数之间呈现非线性相关关系,考虑用非线性多因素拟合回归分析确定多物料破碎模型系数。另外,考虑到在层压破碎实验过程中,每次都需要对石子压碎仪进行振动夯实,并且岩石物料本身可能会有裂痕,所以,在实验中可能有异常的实验数据出现,若用普通最小二乘法估计模型中的参数,则参数的估计值受异常值的影响较大,而采用加权最小二乘法估计模型中的参数,受异常值的影响较小。最终利用非线性拟合回归得到关于物料抗压系数、压缩比和粒度分布系数的多物料破碎力模型:

式中:a1=1.037 8;a2=0.307 1;a3=7.875 2;a4=0.889 1;a5=1.111 7。根据多物料破碎力数学模型,分别绘制石灰石、铁矿石、花岗岩和玄武岩的模型曲面,如图 4所示。从图4可见:物料破碎力随着粒度分布系数增大而增大。这是由于当物料粒度分布范围较大时,小颗粒物料会进入大颗粒物料之间的空隙,并在挤压破碎过程中对大颗粒物料起保护作用;随着物料抗压强度系数的增加,其模型曲面的曲率越大,即在同样的压缩比和粒度分布条件下,抗压强度系数越大,其破碎力也越大。
1.4破碎力模型实验验证
为检验多种物料碎力模型的可靠性与实用性,利用以下几组数据作为检测样本,对多种物料在不同的压缩比和粒度分布情况下进行实验测试,并将每组实验所得的压缩比和粒度代入式(5)得到破碎力的预测值,然后将实验实测结果与模型计算预测值进行比较,如表3所示。
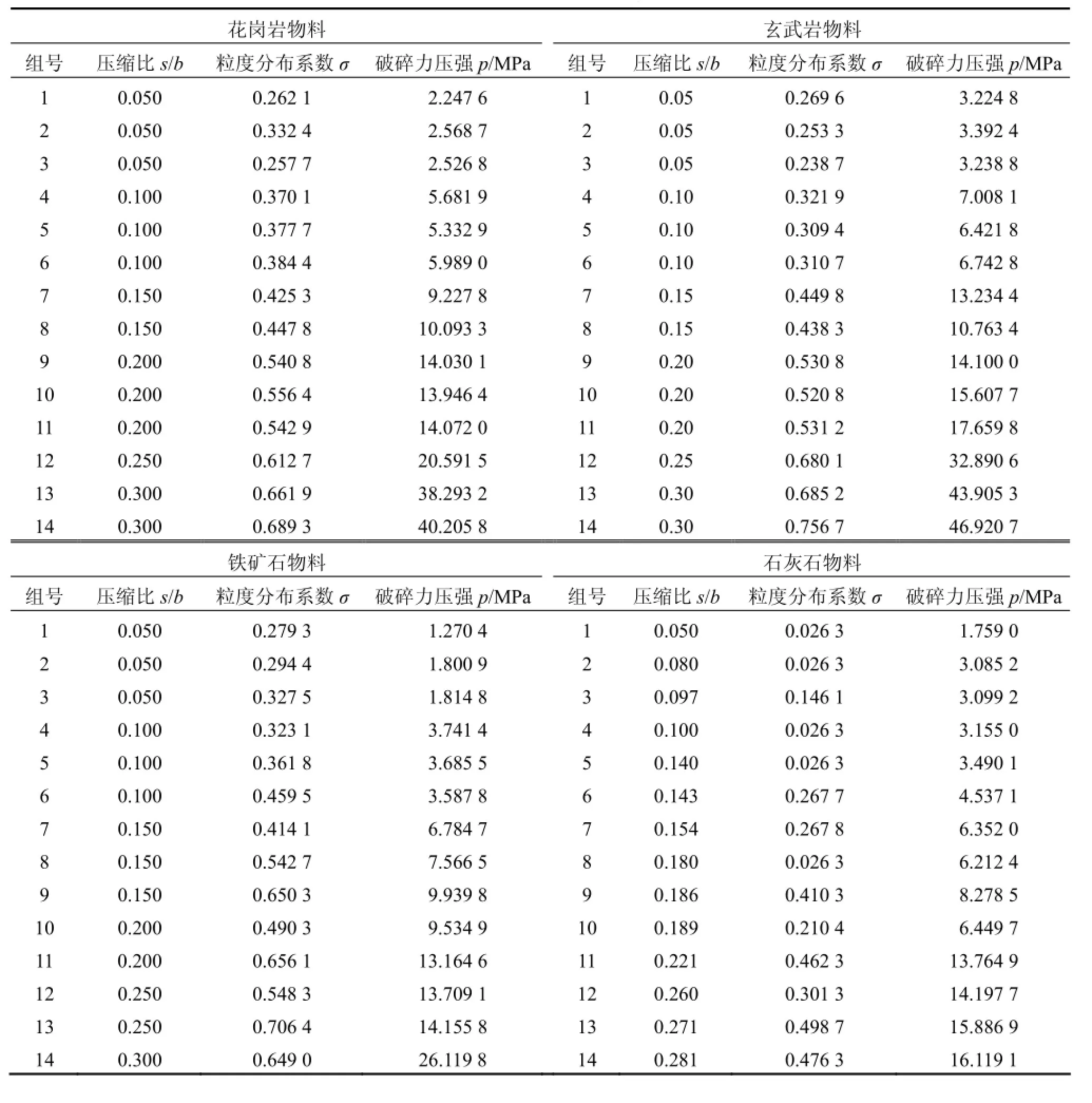
表2 挤压破碎实验结果Table 2 Results of crushing experiment
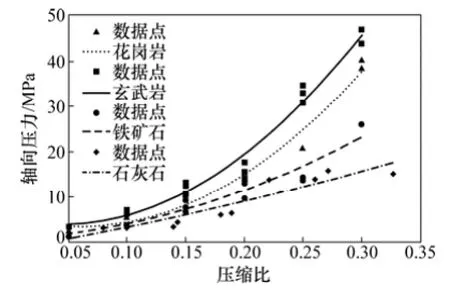
图3 单因素的多物料轴向压力与压缩比的关系Fig. 3 Relationship between pressures of single factor multi-material crushing and compressive ratio

图4 多物料破碎力模型Fig. 4 Multi-material crushing pressure model
从表3可以看出:4种矿石的实验误差最大值分别为2.280,-2.659,2.391和1.792 MPa,建立的多物料挤压破碎力模型预测的破碎力压强与实测压强基本吻合,能够满足实际工程的需求。产生误差的原因是实验过程中部分岩石物料内部可能存在较大的裂痕,或者个别颗粒风化严重而造成压强实验值和预测值之间存在稍大偏差。总体上,所建立的多物料破碎力模型可以用于实际物料挤压破碎过程中对破碎力压强进行预测计算。

表3 物料破碎力压强预测值和实测值对比Table 3 Comparison of crushing pressure between prediction and measurement MPa
2 破碎腔时变磨损模型建模
破碎机在工作过程中,破碎腔表面的破碎衬板将随工作时间的增大和物料处理量的累积而发生磨损,其主要与破碎腔衬板、物料的种类及破碎腔表面破碎力的分布有关,其中,破碎腔表面沿高度方向的磨损趋势与挤压破碎力的分布有关[10-11, 16-22]。破碎腔上物料破碎力可以分解为法向分量和切向分量,破碎腔任意位置的磨损量与破碎力合力呈正比关系。为了建立整个破碎腔的时变磨损模型,首先研究破碎腔平行区部分的磨损量与时间的经验模型[23]。该模型与单位时间内的产量相关,并呈现正比关系,因此,可以推导出假定的时变磨损模型形式,即破碎腔的第i层在工作一段时间后的磨损量为其中:Pn,i为第 i层挤压破碎力压强的法向分量;Ps,i为第i层挤压破碎力压强的切向分量;W为切向力修正系数,表示切向力在破碎衬板在磨损过程中所起的作用,由破碎装备工作参数和结构参数决定,也可由实际数据拟合获得;Pn,p为圆锥破碎机平行区内挤压破碎力压强的法向分量;Ps,p为圆锥破碎机平行区内挤压破碎力压强的切向分量;μ为衡量圆锥破碎机破碎腔磨损系数。将式(5)所示多物料破碎力模型和破碎力分量代入式(6),得到破碎腔的时变磨损模型表达式:
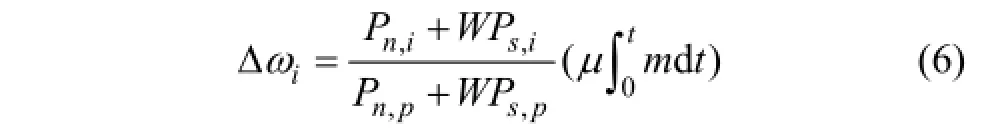
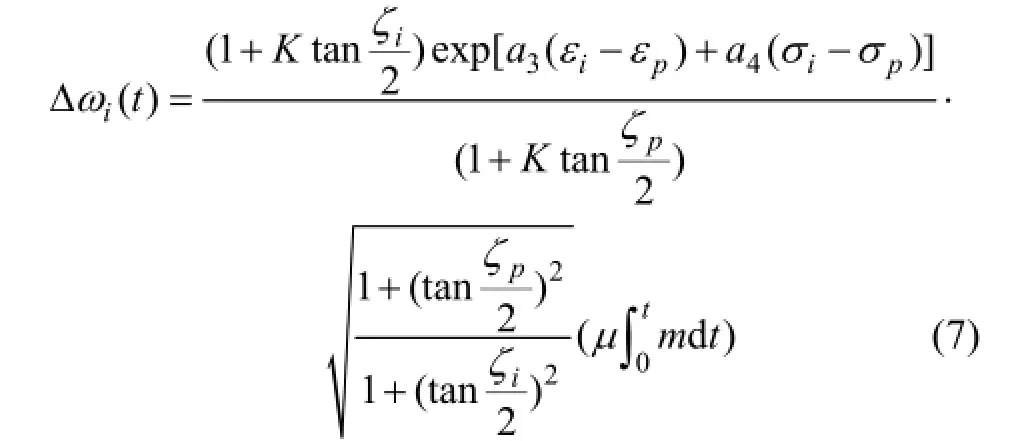
其中:ζi为圆锥破碎机第i层的拟合角;ζp为圆锥破碎机平行区的啮合角;
为t时刻破碎腔第i层的磨损量。为获得所建立模型系数 μ,在马鞍山矿石破碎现场对某型号的圆锥破碎机进行物料破碎实验。基于实测数据确定该模型的系数,该矿石破碎厂每天工作时间为15 h,对圆锥破碎机的闭边排料口3 d调整1次,磨损的实验数据如表4所示。
采用表4中圆锥破碎机的实验条件进行实验,可以得到破碎腔随工作时间增加时的磨损量、闭边排料口宽和总产量等实验结果,利用回归分析计算式(7)中磨损量模型系数μ,μ=0.361 8 kt/h,该磨损系数与圆锥破碎机的结构和破碎衬板的材料相关。
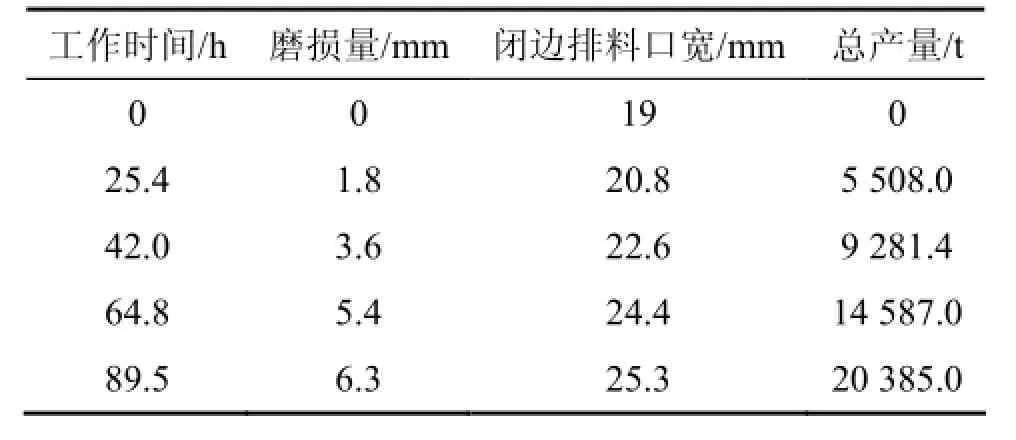
表4 破碎腔闭边排料口处磨损量Table 4 Wear of near point of closed edge of crusher
3 时变磨损模型的应用
为了验证模型的有效性,在安徽马鞍山某采石场的安山岩加工生产线进行实验验证。该采石厂采用鄂式破碎机和圆锥破碎机对安山岩物料进行生产加工,其中二破和回笼分别采用2种不同型号圆锥破碎机,该型号破碎机为上海某破碎机公司制造。本文计算的相关参数与设备的工作参数一致。实验是以回笼的圆锥破碎机为实验对象,破碎物料为安山岩,其抗压强度为110~140 MPa,该生产线的生产时间为每天18 h左右,将中间停机及空转时间除去,实际生产时间大约为15 h。实验步骤如下。
1) 将圆锥破碎机排料口调整到16 mm,启动安山岩破碎生产线的各个设备,开始进行破碎作业。
2) 破碎生产线上各个设备正常工作0.5 h以上,开始对圆锥破碎机的性能参数进行记录。对该设备的排料产品取定量样品约15 kg,每隔1 h取1次,并对该时间内的破碎产品进行筛分分析,记录标定排列粒度。
3) 在破碎生产线各个设备运行正常情况下,连续记录破碎机工作22.5 h时的生产性能数据,然后调整排料口直径。
4) 破碎机闭边排料口直径减少1.8 mm,重复实验步骤1)~3)。
5) 记录各次破碎腔磨损量实验值并进行整理,利用磨损量对磨损模型进行验证。实验结果如表6所示。
根据生产线中圆锥破碎机的结构参数和层压破碎理论,对其破碎腔型进行分层划分,并将结构参数和实验测试数据代入式(7)进行求解,得到预测的磨损量如表5所示。
从表5可以看出破碎腔模型预测的磨损量和实测的磨损量基本吻合,相对误差最大为 7.64%。存在误差的原因比较复杂,如在实际生产中,喂料过程持续波动造成破碎机并不一定满负荷生产,岩石的抗压强度也很不均匀。在模型中未考虑到喂料的波动和岩石抗压强度不均对破碎腔磨损的影响,因此,模型计算值存在一定的误差。但总体而言,实际测量结果在一定程度上证实了破碎腔时变磨损模型的有效性。

表5 圆锥破碎机磨损量预测与实验结果对比Table 5 Wear data comparison between prediction data and teat data
4 结论
1) 利用 RMT-150B岩石力学实验系统对圆锥破碎机层压破碎过程进行实验模拟,并分析影响破碎力的参数,建立了关于抗压强度、压缩比和粒度分布系数的多种物料破碎力模型;以实验采集数据为基础,运用非线性多因素回归分析确定模型中系数。
2) 基于多种物料破碎力模型,提出了圆锥破碎机腔型的时变磨损模型形式,并利用现场实验数据确定了该模型的相关系数。
3) 针对现场矿石破碎生产线中某型号圆锥破碎机,实现了对破碎腔磨损量的预测。所建立的多物料破碎力模型和腔型时变磨损模型为圆锥破碎机的磨损补偿提供了一种有效的方法,也为矿石加工生产线的动态仿真提供了理论模型。
[1] ATTA K T, JOHANSSON A, GUSTAFSSON T. Control oriented modeling of flow and size distribution in cone crushers[J]. Minerals Engineering, 2014, 56(1): 81-90.
[2] ASBJÖRNSSON G, HULTHÉN E, EVERTSSON M. Modelling and simulation of dynamic crushing plant behavior with MATLAB/Simulink[J]. Minerals Engineering, 2013, 43/44(1):112-120.
[3] ITÄVUO P, VILKKO M, JAATINEN A, et al. Dynamic modeling and simulation of cone crushing circuits[J]. Minerals Engineering, 2013, 43/44(1): 29-35.
[4] LEE E, EVERTSSON M. Implementation of optimized compressive crushing in full scale experiments[J]. Minerals Engineering, 2013, 43/44(1): 135-147.
[5] NUMBI B P, XIA X. Optimal energy control of a crushing process based on vertical shaft impactor[J]. Applied Energy,2016, 162(1): 1653-1661.
[6] MAGNUS B, ERIK H, MAGNUS E C. Size and shape simulation in a tertiary crushing stage, a multi objective perspective[J]. Minerals Engineering, 2015, 77(1): 72-77.
[7] LINDQVIS M, EVERTSSON C M. Prediction of worn geometry in cone crushers[J]. Minerals Engineering, 2003, 16(12):1355-1361.
[8] LINDQVIST M, EVERTSSON C M. Liner wear in jaw crushers[J]. Minerals Engineering, 2003, 16(1): 1-12.
[9] LINDQVIST M, EVERTSSON C M. Improved flow- and pressure model for cone crushers[J]. Minerals Engineering, 2004,17(11/12): 1217-1225.
[10] LINDQVIST M, EVERTSSON C M. Development of wear model for cone crushers[J]. Wear, 2006, 261(3/4): 435-442.
[11] 董钢, 范秀敏, JOHANNES N. 圆锥破碎机挤压破碎力建模与衬板磨损预测[J]. 上海交通大学学报, 2011, 45(1): 45-49. DONG Gang, FAN Xiumin, JOHANNES N. Modeling crushing pressure and liner wear of cone crusher[J]. Journal of Shanghai Jiao Tong University, 2011, 45(1): 45-49.
[12] 董钢, 范秀敏, 黄东明. 基于产品质量控制预测机制的圆锥破碎机优化方法[J]. 机械工程学报, 2010, 46(3): 152-157. DONG Gang, HUANG Dongming, FAN Xiumin. Cone crusher optimization based on quality control and prediction[J]. Journal of Mechanical Engineering, 2010, 46(3): 152-157.
[13] 黄冬明. 挤压类破碎机工作机理和工作性能优化研究[D]. 上海: 上海交通大学机械与动力工程学院, 2007. HUANG Dongming. Research on working mechanism and working performance optimization of compressive crusher[D]. Shanghai: School of Mechanical and Power Engineering Shanghai Jiao Tong University, 2007.
[14] DONG Gang, HUANG Dongming, FAN Xiumin. Cone crusher chamber optimization using multiple constraints[J]. International Journal of Mineral Processing, 2009, 93(2): 204-208.
[15] DONG Gang, FAN Xiumin, HUANG Dongming. Analysis and optimization of cone crusher performance[J]. Minerals Engineering, 2009, 22(12): 1091-1093.
[16] JOHANNES Q, MAGNUS E C. Cone crusher modelling and simulation using DEM[J]. Minerals Engineering, 2016, 85(1):92-105.
[17] DELANEY G W, MORRISON R D, SINNOTT M D, et al. DEM modelling of non-spherical particle breakage and flow in an industrial scale cone crusher[J]. Minerals Engineering, 2015, 74(1): 112-122.
[18] CLEARY P W, SINNOTT M D. Simulation of particle flows and breakage in crushers using DEM.Part 1:compression crushers[J]. Minerals Engineering, 2015, 74(1): 178-197.
[19] SINNOTT M D, CLEARY P W. Simulation of particle flows and breakage in crushers using DEM. Part 2: impact crushers[J]. Minerals Engineering, 2015, 74(1): 163-177.
[20] 马彦军, 范秀敏, 何其昌, 等. 圆锥破碎机破碎质量的粒度和粒形数学建模[J]. 机械工程学报, 2013, 49(6): 95-102. MA Yanjun, FAN Xiumin, HE Qichang, et al. Mathematical modeling of particle size and particle shape of crushing quality for cone crusher[J]. Journal of Mechanical Engineering, 2013,49(6): 95-102.
[21] 董钢, 范秀敏, 张曦, 等. 基于层压破碎理论的圆锥破碎机破碎力分析及运动学研究[J]. 机械工程学报, 2010, 46(17):159-164. DONG Gang, FAN Xiumin, ZHANG Xi, et al. Crushing force and kinematics analysis of cone crusher based on interparticle breakage[J]. Journal of Mechanical Engineering, 2010, 46(17):159-164.
[22] 黄冬明, 武殿梁, 范秀敏, 等. 圆锥破碎机的多目标规划设计[J]. 机械工程学报, 2007, 43(3): 204-211. HONG Dongming, WU Dianliang, FAN Xiumin, et al. Design for multiobjective planning of cone crusher[J]. Journal of Mechanical Engineering, 2007, 43(3): 204-211.
[23] ASBJÖRNSSON G, HULTHÉN E, EVERTSSON M. Modelling and dynamic simulation of gradual performance deterioration of a crushing circuit including time dependence and wear[J]. Minerals Engineering, 2012, 33(1): 13-19.
(编辑 陈灿华)
Wear prediction of multi-material time-varying chamber of cone crusher
MA Yanjun, FAN Xiumin, HE Qichang
(State Key Laboratory of Mechanical System and Vibration, School of Mechanical Engineering,Shanghai Jiao Tong University, Shanghai 200240, China)
In order to analyze and calculate crushing quality and support for cone crusher optimization design,RMT-150B rock mechanics test system was used to simulate the interparticle breakage process of cone crusher. A multi-material crushing model was built by experimental research based on the compressive strength, compressive ratio and size distribution index. The kinematics of rock material in the crushing chamber was analyzed by the inter-particle breakage theory. A time-varying chamber wear model was obtained by studying the chamber wear of a crushing circuit. Experimental results of chamber wear and solving results of time-varying chamber wear model were comparatively analyzed. The results show that the model can be used to solve wear cone crusher, the wear of the model is consistent with the research results, and the prediction of wear can be realized.
cone crusher; crushing pressure; wear; size distribution; crushing circuits
TD451
A
1672-7207(2016)04-1121-07
10.11817/j.issn.1672-7207.2016.04.006
2015-04-10;
2015-06-21
上海市科学技术委员会资助项目(12DZ1125302)(Project (12DZ1125302) supported by the Science and Technology Committee of Shanghai City)
马彦军,博士研究生,从事机械系统最优化设计及虚拟样机技术研究;E-mail:kfmyj@sjtu.edu.cn

