BR1500HS 超高强度钢本构模型的建立及验证
夏玉峰,纪帅,张严东
(重庆大学 材料科学与工程学院, 重庆,400044)
BR1500HS 超高强度钢本构模型的建立及验证
夏玉峰,纪帅,张严东
(重庆大学 材料科学与工程学院, 重庆,400044)
在Gleeble3500热模拟实验机上,采用等温热拉伸实验对BR1500HS超高强度钢在变形温度为1 023,1 073,1 123和1 173 K,应变速率为0.01,0.10和1.00 s-1条件下的热流变行为进行研究。根据蠕变理论及实验流动应力曲线确定材料变形激活能、硬化指数等相关材料常数并引入 Zener-Hollomon参数。通过位错密度演化模型描述加工硬化和动态回复对流动应力的影响,并建立包含稳态应力σss、屈服应力σ0和动态回复速率系数r这3个参数的本构模型。研究结果表明:由建立的本构模型所绘制的流动应力曲线与实验曲线具有高度一致性,所建立的本构模型能够应用于BR1500HS超高强度钢热拉伸过程的数值模拟及热成形工艺分析。通过回归分析法建立模型参数关于Z参数的表达式,获得流变应力与变形条件的关系。
BR1500HS超高强度钢;动态回复;Z参数;本构模型
近年来,随着世界汽车保有量与日俱增,随之而来的能源短缺、环境污染等一系列问题也日益突出,提高汽车安全性、车身轻量化、降低油耗成为世界汽车工业界的共同目标。在此形势下,超高强度钢板以其质量轻、强度高、成本低的特点在汽车业中受到广泛的关注,采用超高强度钢板代替传统钢板材料来制造车身结构件已成为实现车身轻量化和提高汽车安全性的主要途径。但超高强度钢板在常温下的成形性很差,采用传统的冷冲压成形方法会出现易拉裂、成形载荷过大、回弹严重等问题[1-3]。针对这些问题,热冲压作为一项新的专门应用于成形超高强度冲压件的制造技术有效地解决了上述问题,可生产出高精度、高强度的汽车构件。目前,国内外关于热冲压的研究主要集中于变形温度、压边力、润滑系数、冷却速度等工艺参数对热冲压件微观组织和力学性能的影响[4-7],关于化学成分对超高强度钢板成形性和力学性能的影响也有大量的报道[8-12],而关于热成形的基础研究却鲜有报道。在热冲压成形过程中,板料的热流变应力在加工硬化和动态回复及动态再结晶软化的共同影响下发生复杂的变化,板料的热变形行为将直接影响板料的成形性能及成形件最终强度。本构关系以函数的形式揭示了材料流变应力与变形温度、应变速率以及真应变等变形条件之间的关系。热变形过程中应力决定了材料在变形中所需要负荷和消耗能量,是进行塑性加工工艺设计的基础,也是设备选取的重要依据,且合理的本构模型是有限元数值模拟具有实际指导意义的必要条件。因此,对BR1500HS超高强度钢的热流变行为展开研究并建立合理的本构模型,对确定BR1500HS超高强度钢的加工工艺规范及进行有限元数值模拟均具有重要的意义。国内外已有大量关于其他金属材料本构关系的研究。李瑞卿等[13]采用等温压缩实验研究了 Cu-Cr-Zr-Ce合金在变形温度为 873~1 073 K、应变速率为0.01~5.00 s-1条件下流变应力与变形温度和应变速率之间关系的本构方程,并提出动态回复是其变形过程中主要的软化机制。张雪敏等[14]通过对TC11钛合金进行等温恒应变速率压缩实验获得了合金的真应力真应变曲线,在Arrheninus双曲正弦方程的基础上建立了适用于TC11钛合金热变形的本构方程。只悦胜等[15]针对20GrMnTiH钢,建立了Z参数与峰值应力、峰值应变之间的表达式,并通过引入应变软化指数,对整个应变区间上的应变与软化指数进行非线性拟合,建立了应力与应变之间的关系,推导出基于应变软化的本构方程。张新明等[16]分析了幂函数、指数函数和双曲正弦函数半经验本构方程对Mg-6Gd-3Y-0.5Zr合金变形行为的适用性,并指出由于合金中高温耐热相提高了合金高温下的强度,指数函数的拟合精度高于幂函数和双曲正弦函数。包军等[17]利用 Gleeble3800热模拟试验机对热冲压硼钢板进行热拉伸实验,获得了该材料的真应力-真应变曲线,并建立了考虑温度和应变速率影响的热流变方程。当前关于本构模型的研究大多是基于连续介质力学和不可逆热力学理论的宏观唯相法,而从位错密度、晶粒粒径等微观结构入手,基于变形机理的微观力学方法的研究较少,且两者结合的方法也较少。在本项研究中,以 BR1500HS超高强度钢为研究对象,在Gleeble3500热模拟试验机上进行热拉伸实验,获得超高强度钢在不同变形条件下的真应力-真应变曲线,分析了材料在高温下的热流变特点。利用宏观唯相法求解出相关的材料常数及Z参数,从位错密度演化模型入手揭示了不同条件下材料流变应力的变化特点,并建立了包含3个未知参数的材料本构模型。通过回归分析的方法求解出模型中未知参数与Z参数的函数关系,进而建立了仅包含温度、应变、应变速率3个变量而不包含其他未知参数的本构方程。
1 实验材料及方法

图1 高温条件下的热拉伸试样Fig. 1 Tensile test specimen used in uniaxial tensile testing at elevated temperature
实验采用由宝钢生产的BR1500HS热轧钢板。根据金属材料高温拉伸国家标准GB/T 4338—2006[18],制备如图1所示的方形热拉伸试样。为避免加工硬化对材料拉伸性能的影响,所有试样均采用线切割的方法进行加工。此外,在试样两端各钻一个直径为8 mm的定位孔以避免热拉伸时试样滑动。用细砂纸打磨掉试样表面的加工纹路,以免拉伸时出现应力集中。在试样表面中心部位焊接与热模拟试验机相连的热电偶以实现温度实时监测与控制。拉伸实验在一台Gleeble3500热模拟试验机上进行,Gleeble3500采用独特的电阻加热系统可实现快速加热和保温,高热导率的夹具可以实现高速冷却,采用热电偶为试样温度反馈控制提供数据,热拉伸过程具体的温度控制和实验流程如下:1) 试样以5 K/s的速度加热到1 173 K。2) 在1 173 K保温300 s使组织充分奥氏体化。3) 试样以15 K/s的速度分别冷却至成形温度1 173,1 123,1 073和1 023 K并保温10 s以消除内部温度梯度。4) 在不同变形温度下(1 173,1 123,1 073和1 023 K)分别以0.01,0.10和1.00 s-1的应变速率进行恒温等应变速率拉伸,直至拉断。
在实验过程中,由 Gleeble3500热模拟试验机的微机处理系统自动采集应力应变数据,图2所示为实验的工艺路线。

图2 实验工艺路线Fig. 2 Test project
2 实验结果与分析
2.1流变行为的特征描述

图3 不同变形条件下的真应力-真应变曲线Fig. 3 True stress-strain curves at different deformation conditions
图3所示为BR1500HS超高强度钢板在不同变形温度和应变速率下的真应力-真应变曲线。由图 3可知:所有曲线中的应力均随着应变的增加而增加,并最终几乎保持在一个稳定的水平,是典型的以动态回复为主要软化机制的应力-应变曲线[17]。此外,变形温度和应变速率对BR1500HS钢的流变应力都有显著的影响。对比以上应力-应变曲线很容易发现:在较低温度及较高应变速率下,钢的峰值应力较高;应变速率的减小或变形温度的升高均会使峰值应力降低;在恒定的变形温度下,相同应变对应的流变应力随着应变速率的增加而增加,这是因为应变速率的增加会增大位错的生成速度,增加位错密度,提高材料的硬化特性;与之相反,在恒定的应变速率下,相同应变所对应的流变应力会随着温度的升高而显著降低,这是因为温度升高会增加原子动能,激活更多位错的滑移和攀移,增加动态回复速率,更大程度上抵消加工硬化的影响。且流变应力随着应变的增加可以分为 3个阶段:第1阶段,加工硬化占主导作用,应力随着应变的增加近似线性地增加到一个临界值;第2阶段,动态回复及动态再结晶等软化机制发挥越来越重要的作用,应力增加的速率越来越小,最后由于加工硬化和动态回复等引起的软化达到动态平衡,流变应力保持在一个稳定的水平;第3阶段,试样缩颈引起局部变形,流变应力随着应变的增加快速下降直到材料断裂如图4所示。

图4 拉伸试样的缩颈及断裂示意图Fig. 4 Schematic diagram of necking and fracture of tensile test specimen
2.2BR1500HS超高强度钢材料常数的求解
金属材料的热变形与高温蠕变相似,存在热激活过程,其变形机制是不同应力水平下蠕变机制的扩展。变形温度和应变速率对变形的影响可通过下式包含变形激活能的蠕变方程来表达[20]:
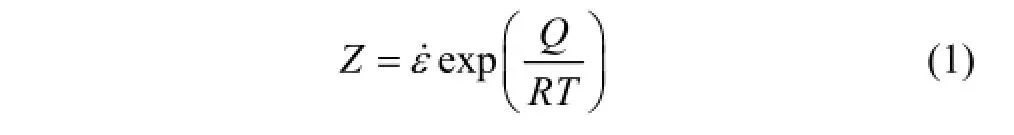
由图3可知:金属热拉伸过程中的稳态应力值取决于变形温度和应变速率。如以下所示的 Arrhenius方程被广泛地用来描述他们之间的关系[21]:

式中:Z为Zener-Hollomon参数,其物理意义是温度补偿的应变速率因子;ε˙为应变速率;R为气体摩尔常数;T为热力学温度;Q为反映材料变形难易程度的变形激活能;σss为稳态应力;A,α,n和m为与温度无关的材料常数,α=β/n。通常式(2)适用于低应力水平,式(3)适用于高应力水平,而如式(4)和式(5)所示的双曲正弦方程适用于描述各种应力状态下Z与稳态应力的关系。

同时对式(2)~(4)两端取自然对数分别得:


图5 与lnσss,σss的关系Fig. 5 Relationships betweenand lnσss, σss


图6 ln(sinh(ασss˙))与
2.3表征动态回复行为的本构模型
以动态回复为主要软化机制的金属在进行热拉伸等变形时, 金属材料的热变形性能取决于材料的位错堆积、亚晶生成及亚晶多边形化等微观组织演变。随着应变的增加,材料的位错密度会在加工硬化和动态回复的影响下而相应地增加和减小。因此,材料位错密度的变化可表示为加工硬化和动态回复软化所对应的位错密度变化之和,即



如果把塑性变形之前的材料位错密度定义为ρ0,则c可通过计算获得,故

根据LIN等[23]关于黏塑性理论的研究, 流变应力和位错密度具有如下关系:

或

因此,屈服应力σ0可表示为

式中:α为材料结构系数;μ为剪切模量;b为伯格矢量的级数;ρ0为初始位错密度。
以动态回复为主要软化机制的材料,在进行恒温等应变速率热拉伸过程中,随着应变的增加,加工硬化和动态回复软化将达到动态平衡,与之相应材料的流变应力也会达到一个稳态值 σrec。结合式(12)和式(14),可求解稳态值σrec,即

综合以上分析,由式(13)~(16)可得以动态回复为主要软化机制的材料的本构方程为

式中:σ0和 σrec分别为屈服应力和饱和应力,可通过实验曲线分别求解。
2.4模型参数的确定及验证
由式(18)可知:要求解上述表征动态回复和加工硬化行为的本构模型,需要确定σ0,σrec和r这3个参数,对式(18)进行微分可得

由式(18)和式(19)可得

即

取σθ和σ2的数值分别为y3和x4,图7所示为当变形温度为1 023,1 073,1 123和1 173 K时的σθ-σ2曲线,其中θ=dσ/dε。由式(21)可知:-0.5r和分别与直线部分的斜率和截距相对应,因此,r和可通过对σθ-σ2进行线性回归求解。表1和表2所示分别为r和
的值。由于r和σrec已经确定,通过待定系数法对应力应变数据进行回归分析即可得屈服应力σ0,表3所示为不同变形条件下σ0的值。将r,σ0和 σrec分别代入式(18)即可求得能够表征 BR1500HS超高强度钢板动态回复和加工硬化行为的本构模型,并可绘制相应的模型曲线,图8所示为实验曲线和模型曲线的对比。由图8可知:在变形的前2个阶段,模型曲线与实验曲线具有高度的一致性;随着应变的增加,模型曲线和实验曲线开始分离。这是因为热拉伸过程出现了缩颈及断裂,使应力迅速下降。以上分析表明所建立的本构模型能准确地反映材料在不同变形情况下应力的变化情况。
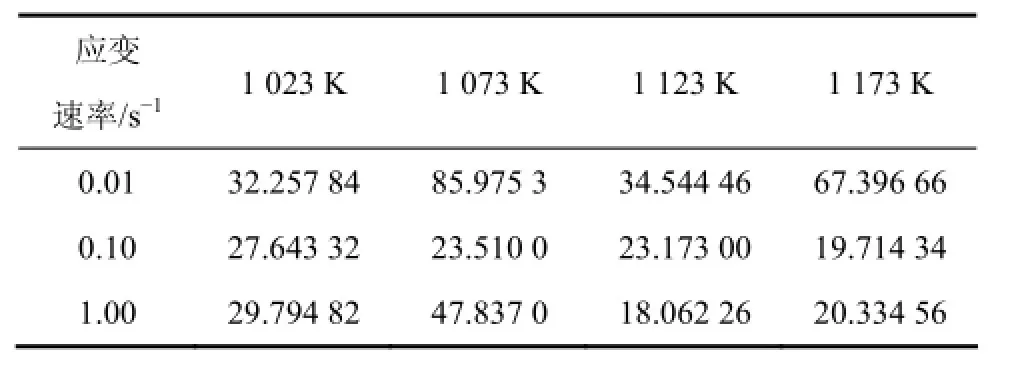
表1 动态回复系数r的值Table 1 Values of dynamic recovery coefficient r
Table 2
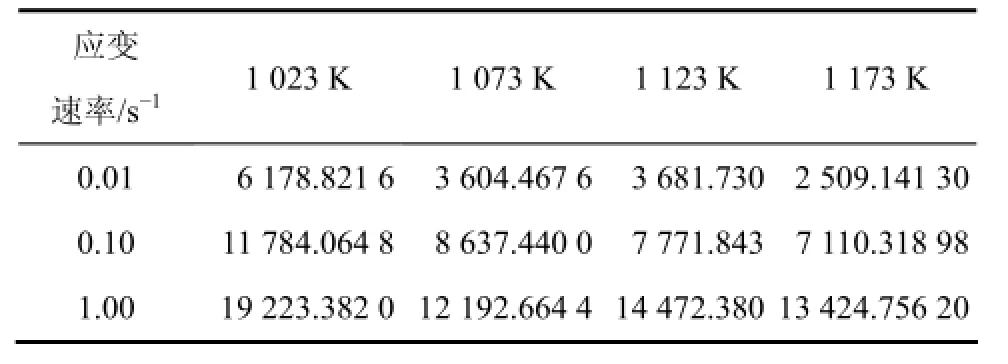
Table 2
应变速率/s-1 1 023 K 1 073 K 1 123 K 1 173 K 0.01 6 178.821 6 3 604.467 6 3 681.730 2 509.141 30 0.10 11 784.064 8 8 637.440 0 7 771.843 7 110.318 98 1.00 19 223.382 0 12 192.664 4 14 472.380 13 424.756 20

图7 不同变形条件下的σθ-σ2曲线Fig. 7 σθ-σ2curves under different deformation conditions

图8 不同变形条件下实验曲线与模型曲线的对比Fig. 8 Comparisons of experimental curves with model ones under different deformation conditions

表3 σ0的值Table 3 Values of σ0MPa
2.5模型参数与变形条件的关系
温度补偿系数Z是应变速率和变形温度的函数,可表征温度和应变速率对材料变形性能的综合影响。由式(1)可知:应变速率越大,变形温度越低,Z越大。图9(a)所示为动态回复系数r与温度补偿参数Z的关系。由图9(a)可知:r随着Z的升高而降低,这可归结于以下3个原因:1) 大的应变速率会增加位错的增殖速度,增大材料强化特性,降低回复软化效果;2) 增加应变速率会减少变形所需的时间,动态回复没有足够的时间表现;3) 动态回复是位错交滑移、攀移而导致的亚晶生成、亚晶多边形化的结果,而位错的滑移、攀移是热激活、热扩散的过程,低的成形温度显然不利于位错的运动。图9(a)表明lnr与lnZ为线性相关,通过线性回归可得r与Z具有如下的关系:

根据式(1)即可建立动态回复系数与变形条件的关系。图10(a)以三维图的形式表明了变形温度和应变速率对动态回复系数r的综合影响。
屈服应力是材料发生塑性变形的临界应力,在达到临界应力之前材料发生弹性变形,应力随着应变的增加而线性地增加。图9(b)所示为屈服应力σ0与Z的关系。由图9(b)可知:屈服应力σ0随着Z的增加而增加。这是因为材料的塑性变形机制主要是位错的滑移,而低温高应变速率即较大的β会造成位错大量堆积,增加位错密度,增大位错开动所需要的应力。通过线性回归可得σ0与Z具有如下的关系:

根据Z的定义可取得屈服应力与变形条件间的关系,图10(b)以三维图的形式表明了变形温度和应变速率对屈服应力σ0的综合影响。

图9 lnZ与lnr,σ0的关系Fig. 9 Relationships between lnZ and lnr, σ0

图10 变形条件与r,σ0的关系Fig. 10 Relationships between deformation conditions and r, σ0
因动态回复是超高强度钢的主要软化机制,由图8可知:σss与 σrec差别很小,所以可以用σss近似代替σrec,由式(1)和式(8)可建立σss和Z的关系,即

图11所示为lnZ和ln(sinh(ασss))之间的线性关系,通过线性回归分析可得 m和 A2分别为 5.322 55和4 017 193 115。由式(24)和双曲正弦函数的定义式可以将稳态应力σss表示为温度补偿参数Z的函数,即

将α,m和A2代入式(25),稳态应力σss可写为

图11 lnZ与ln(sinh(ασss) )的关系Fig. 11 Relationship between lnZ and ln(sinh(ασss))
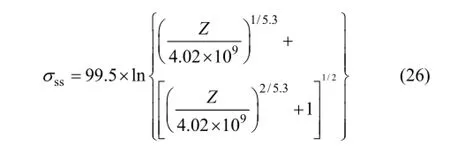
由以上的分析可知,本构模型中的未知参数均可以通过Z而建立与变形条件之间的函数关系,因此,由式(17),式(21),式(22)与式(25)可建立 BR1500HS超高强度钢在应变速率为 0.01~1.00 s-1、变形温度为1 023~1 173 K条件下的仅含变形温度,应变速率和应变3个参数的本构模型为

3 结论
1) 在温度为1 023~1 173 K、应变速率为0.01~1.00 s-1下,BR1500HS超高强度钢的热变形行为表现为应变硬化加动态回复机制,变形温度和应变速率对其热流变行为均有显著影响。
2) BR1500HS超高强度钢的平均热变形激活能为221.87 kJ/mol。
3) 建立BR1500HS超高强度钢的本构模型,将模型结果与实验结果进行了比较,证实了该模型能够较好地描述不同变形条件下钢的热流变行为。
4) 建立稳态应力、屈服应力、动态回复系数与Z的关系,并分析了变形条件对这些参数的影响,将本构模型与变形条件建立直接的联系。
[1] 李辉平, 赵国群, 张雷, 等. 超高强度钢板热冲压及模内淬火工艺的发展现状[J]. 山东大学学报, 2010, 40(3): 69-74.
LI Huiping, ZHAO Guoqun, ZHANG Lei, et al. The development status of hot stamping and quenching of ultra high-strength steel[J]. Journal of Shandong University, 2010,40(3): 69-74.
[2] 邢忠文, 包军, 杨玉英, 等. 可淬火硼钢板热冲压成形实验研究[J]. 材料科学与工艺, 2008, 16(2): 172-175. XING Zhongwen, BAO Jun, YANG Yuying, et al. Hot stamping processing experiments of quenchable boron steel[J]. Materials Science and Technology, 2008, 16(2): 172-175.
[3] 胡平, 马宁. 高强度钢板热成形技术及力学问题研究进展[J].力学进展, 2011, 41(3): 310-334. HU Ping, MA Ning. Development of hot forming technology for ultra-high strength steel and its mechanical problem[J]. Advances in Mechanics, 2011, 41(3): 310-334.
[4] YANAGIDA A, AZUSHIMA A. Evaluation of coefficients of friction in hot stamping by hot flat drawing test[J]. CIRP Annals-Manufacturing Technology, 2009, 58(1): 247-250.
[5] HOFFMANN H, SO H, STEINBESISS H. Design of hot stamping tools with cooling system[J]. CIRP Annals-Manufacturing Technology, 2007, 56(1): 269-272.
[6] LIU Wei, LIU Hongsheng, XING Zhongwen, et al. Effect of temperature and punch speed on hot stamping of ultra-high strength steel[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2): 534-541.
[7] KATSUYOSHI L, JUN Y. Valuation method for effects of hot stamping process parameters on product properties using hot forming simulator[J]. Journal of Materials Processing Technology, 2011, 211(8): 1441-1447.
[8] MEJIA I, BEDOLLA-JACUINDE A, MALDONADO C, et al. Hot ductility behavior of a low carbon advanced high strength steel (AHSS) microalloyed with boron[J]. Materials Science and Engineering A, 2011, 528(13/14): 4468-4474.
[9] JIMENEZ J A, FROMMEYER G, ACOSTA P, et al. Mechanical properties of two ultrahigh carbon-boron tool steels[J]. Materials Science and Engineering A, 1995, 202(1/2): 94-102.
[10] JAE B S, GIL H G, NAM S L, et al. Atomic scale investigation on the distribution of boron in medium carbon steels by atom probe tomography and EELS[J]. Ultramicroscopy, 2010, 110(7):783-788.
[11] ZHANG Z W, LIU C T, GUO S, et al. Boron effects on the ductility of a nano-cluster-strengthened ferritic steel[J]. Materials Science and Engineering A, 2011, 528(3): 855-859.
[12] ZHANG Shiqi, HUANG Yunhua, SUN Bintang, et al. Effect of Nb on hydrogen-induced delayed fracture in high strength hot stamping steels[J]. Materials Science and Engineering A, 2015,626(25): 136-143.
[13] 李瑞卿, 田保红, 张毅, 等. Cu-Cr-Zr-Ce合金高温热变形行为研究[J]. 功能材料, 2013, 44(14): 2036-2046. LI Ruiqing, TIAN Baohong, ZHANG Yi, et al. Hot deformation behavior of Cu-Cr-Zr-Ce alloy at elevated temperature[J]. Journal of Functional Materials, 2013, 44(14): 2036-2046.
[14] 张雪敏, 曹福洋, 岳红彦, 等. TC11钛合金热变形本构方程的建立[J]. 稀有金属材料与工程, 2013, 42(5): 937-941. ZHANG Xuemin, CAO Fuyang, YUE Hongyan, et al.Establishment of constitutive equations of TC11 alloy during hot deformation[J]. Rare Metal Materials and Engineering, 2013,42(5): 937-941.
[15] 只悦胜, 胡成亮, 赵震, 等. 20CrMnTiH 本构模型的建立及验证[J]. 上海交通大学学报, 2013, 47(11): 1697-1701. ZHI Yuesheng, HU Chengliang, ZHAO Zhen, et al. A constitutive model of 20CrMnTiH steel and its validation[J]. Journal of Shanghai Jiaotong University, 2013, 47(11):1697-1701.
[16] 张新明, 吴懿萍, 邓运来, 等. Mg-Gd-Y-Zr合金热变形本构方程[J]. 中国有色金属学报, 2011, 21(12): 2987-2994. ZHANG Xinming, WU Yiping, DENG Yunlai, et al. Constitutive equation during hot compression deformation of Mg-Gd-Y-Zr alloy[J]. The Chinese Journal of Nonferrous Metals, 2011,21(12): 2987-2994.
[17] 包军, 刘红生, 邢忠文, 等. 热冲压硼钢高温下热流变特性[J].材料科学与工艺, 2010, 18(增1): 48-51. BAO Jun, LIU Hongsheng, XING Zhongwen, et al. Flow behavior of boron steel for hot stamping at elevated temperature[J]. Materials Science and Technology, 2010,18(Suppl 1): 48-51.
[18] GB/T 4338—2006, 金属材料: 高温拉伸试验方法[S]. GB/T 4338—2006, Metallic materials: tensile testing at elevated temperature[S].
[19] LIU Juan, CUI Zhengshan, LI Congxing. Modelling of flow stress characterizing dynamic recrystallization for magnesium alloy AZ31B[J]. Computational Materials Science, 2008, 41(3):375-382.
[20] MOMENI A, DEHGHANI K. Hot working behavior of 2205 austenite-ferrite duplex stainless steel characterized by constitutive equations and processing maps[J]. Materials Science and Engineering A, 2011, 528(3): 1448-1454.
[21] JONAS J, SELLARS, MGGW J. Strength and structure under hot working condition[J]. International Materials Reviews, 1969,14(14): 1-24.
[22] CABRERA J M, PONCE J, PRADO M. Modeling thermomechanical processing of austenite[J]. Journal of Materials Processing Technology, 2003, 143/144: 403-409.
[23] LIN Yongcheng, CHEN Xiaomin. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working[J]. Materials and Design, 2011, 32(4):1733-1759.
(编辑 刘锦伟)
A constitutive model for ultrahigh strength steel BR1500HS and its validation
XIA Yufeng, JI Shuai, ZHANG Yandong
(School of Material Science and Engineering, Chongqing University, Chongqing 400044, China)
The deformation behaviors of ultrahigh strength steel BR1500HS at elevated temperature were studied by performing hot tension tests at temperatures of 1 023, 1 073, 1 123 and 1 173 K and strain rates of 0.01, 0.10 and 1.00 s-1on a Gleeble3500 thermo-mechanical simulator. The activation energy, hardening exponent and other material constants were determined by the basic theory of creep and experimental curves, and the Zener-Hollomon parameter was also introduced. The effects of work hardening and dynamic recovery on the flow stress were described through the dislocation evolution model, and the constitutive model containing parameters such as saturated stress (σss), yield stress (σ0) and dynamic recovery coefficient (r) was established. The results show that the model curves are highly in accord with the experimental ones, which shows that the constitutive model is accurate enough to be applied for numerical simulation and provide guide for hot forming process. The relationships between the parameters in constitutive model and Zener-Hollomon parameter can be established by regression analysis, and thus the relationship between flow stress and deformation conditions can be achieved.
ultrahigh strength steel BR1500HS; dynamic recovery; parameter Z; constitutive model
TG142
A
1672-7207(2016)04-1111-10
10.11817/j.issn.1672-7207.2016.04.005
2015-04-15;
2015-06-10
中央高校基本科研业务费专项资金资助项目(CDJZR13130082)(Project (CDJZR13130082) supported by the Fundamental Research Funds for the Central Universities)
夏玉峰,副教授,硕士生导师,从事塑性成形及模具设计研究;E-mail:xyfeng@cqu.edu.cn

