计算多介质电场节点场强的有限元-边界元法

谢裕清，李　琳

(华北电力大学 新能源电力系统国家重点实验室，北京 102206)



计算多介质电场节点场强的有限元-边界元法

谢裕清，李琳

(华北电力大学 新能源电力系统国家重点实验室，北京 102206)

为了解决节点有限元法在多介质电场计算中场域边界及介质分界面处场强计算精度不高的问题，提出了一种有限元-边界元混合算法。该算法首先应用节点有限元法计算多介质场域中的节点电位，然后将场域划分成多个单一介质的子域，子域边界处的电位通过有限元法计算的节点电位映射插值得到。接下来对各个子域分别采用边界元法计算边界处的法向场强，子域内部任意位置的场强则通过边界积分方程计算得到。数值计算结果表明该方法在场域边界以及分界面处节点场强的计算精度比传统的面积加权平均算法高，场域内部节点场强的计算误差也较低。所提方法不仅适合于静电场的计算问题，也适合于其它场强在介质分界面处不连续的矢量场计算问题。

有限元-边界元法；多介质；介质分界面；边界场强

0　引　言

在电磁场数值计算领域中，通过节点有限元方法求解电位函数的理论及技术已经非常成熟，电位的计算精度也较高。然而，怎样通过节点位函数获得较高精度的节点场强一直是学者较为关注的问题。文献[1]从互补变分原理出发得到了求解全域节点场强的有限元离散公式。文献[2]基于面矢基函数，应用加权余量法对电位的梯度函数进行有限元离散，通过散度定理对电位梯度进行转换，避免了直接对电位进行数值微分，提高了计算精度。文献[3-5]基于超收敛理论求得单元内精度最高点的场强，然后利用该点的场强通过插值理论得到网格的节点场强。上述方法对于单一介质模型能够获得较高的计算精度，但是对于多介质模型在分界面处的节点场强的计算效果较差。

在实际工程问题中，静电场场域的边界以及介质交界面处的法向场强是研究介质绝缘问题的重要参数。为了解决节点有限元法不能很好地计算介质分界面处的场强的问题，棱边有限元法得到迅速发展。该方法直接选用场矢量作为求解变量，采用棱单元插值保证场强切向方向连续，而不强制法向方向连续，可以避免通过位函数求解场量而引起的微分误差等问题[6-8]。该方法计算精度较高，但是与节点有限元相比，棱边有限元法计算代价较高。

对于场域边界及内部的场强，边界元法可以得到比较高精度的计算结果。该方法将静电场的边值问题转换成边界积分方程问题，利用有限元离散技术对场域边界进行离散,结合边界积分方程将静电场边值问题转换成代数方程问题求解。该方法仅仅需要对边界单元进行网格剖分，其求解问题的空间维数比有限元低，计算精度高，易处理开域问题等特点[9-13]。然而，边界元法对于多介质模型处理起来也较为困难。

结合有限元以及边界元法的计算优势，本文提出求解多介质静电场节点场强的有限元-边界元混合算法。首先以节点有限元法求解场域节点电位，再以边界元法计算从场域提取的单一介质子域的节点场强。由于子域是由单一介质组成，场域分界面同时也是两个不同子域的交界面，因此可以避免由于介质分界面法向场强不连续而需要在分界面处额外布置节点的困难，从而可以提高介质分界面处的电场强度的计算精度。此外，场域边界处的节点场强也比传统的节点有限元法的计算精度高。

1　有限元-边界元法计算节点场强流程

图1为多介质静电场模型示意图，其包含n种介质，场域边界Γ1满足第一类边界条件，边界Γ2满足第二类边界条件。在静电场数值计算中，电位在场域内处处连续，场域中的电位可以通过节点有限元法得到精度较高的数值解。在介质交界面处，电场强度仅仅切向连续，切向电场强度可以通过电位微分方程计算得到，而法向场强在交界面处不连续，采用电位微分法的方式求得的场强误差较大。

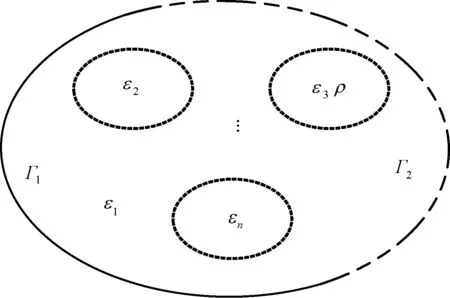
图1　多介质静电场模型Fig.1　Multi-medium static electrical field model

本文结合有限元法与边界元法的特点，提出有限元边界元混合算法计算场域中的节点场强，其计算流程图如图2所示。首先对于整体静电场模型采用有限元网格离散，建立基于电位的节点有限元方程，得到整体场域的节点电位。然后，将场域划分成多个由单一介质构成的子域，提取子域的几何信息。使用边界单元离散子域边界，子域的边界节点电位则通过有限元法求得的场域节点电位映射插值得到。最后，采用边界元法建立关于子域法向场强的边界元方程，求得子域的边界法向场强。由于在介质分界面上电场的切向分量连续，仍然可以通过节点电位的微分进行计算并得到较高精度的解。子域内部任意位置的场强则可以结合子域边界上的节点电位以及节点法向场强通过边界积分方程计算得到。

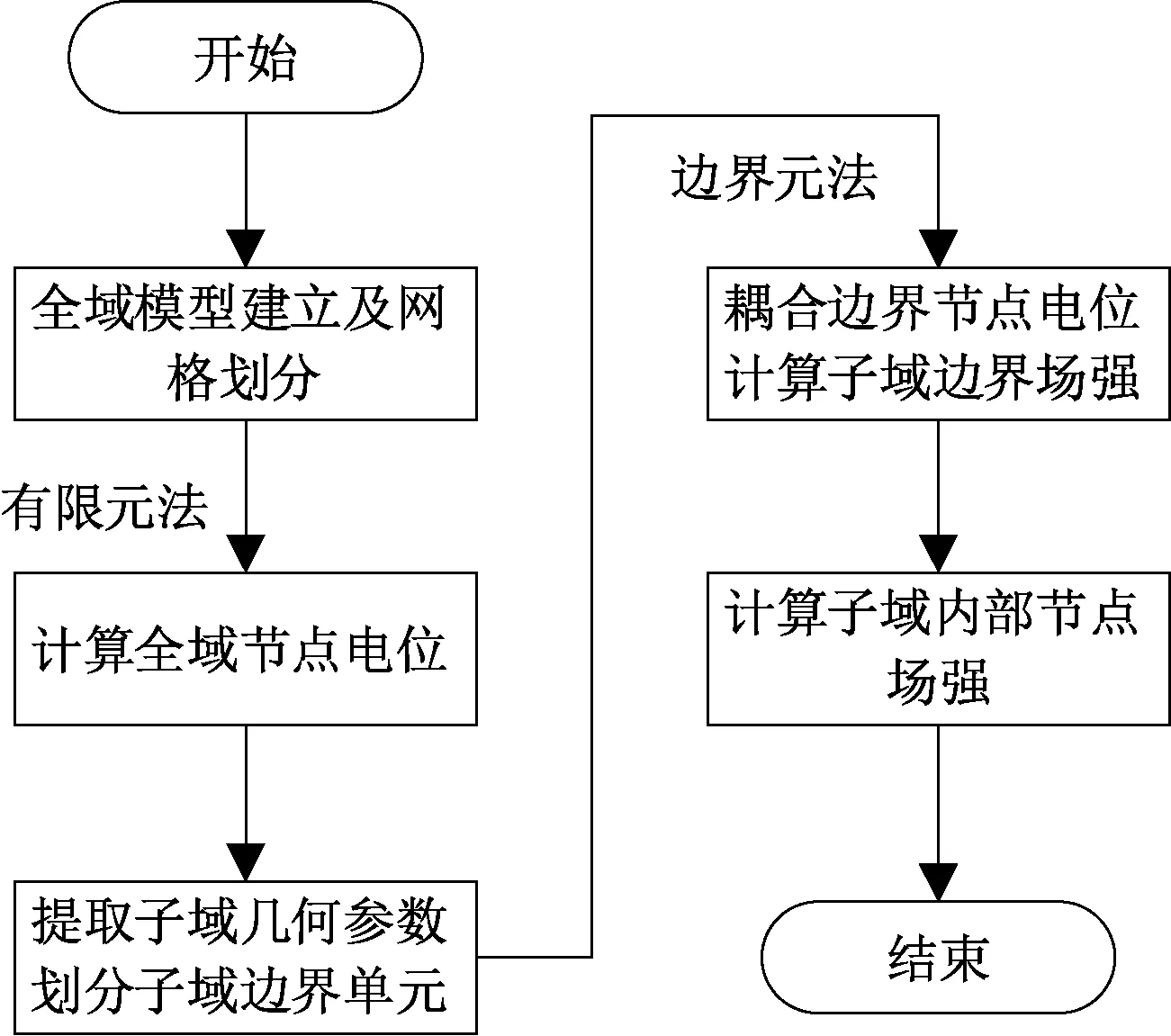
图2　有限元-边界元计算节点场强流程图Fig.2　Flowchart of finite element and boundary element mixed method for solving node electrical field intensity

实际计算过程中，子域的选取可以根据实际计算需要选择，仅需要满足单一介质条件即可。如果仅关注整体场域中某一小部分区域的电场强度情况，可以围绕这部分区域构造子域，此时该子域的计算规模比整体场域的计算规模要小得多，节约了计算资源。

2　有限元法计算全域节点电位

图1所示的多介质电场计算模型，标量电位满足的基本方程及边界条件为

(1)

运用变分原理，将静电场边值问题的微分方程式(1)转化为泛函求极值问题。式(1)所对应的等效极值泛函为[14]

(2)

上式泛函取得极值的解也即偏微分方程(1)式的解，第一类边界条件为变分约束条件。应用有限元单元剖分场域，选取合适的插值函数，构造电位φ的近似函数为

(3)

式中：n为场域离散网格节点总数；Nj为节点电位φj对应的插值基函数。将式(3)带入式(2)，并根据泛函极值条件∂J(φ)/∂φi=0(i=1,2,…,n)，可以得到以节点电位φ1,φ2, …,φn为变量的有限元代数方程组：

(4)

第一类边界条件采用强加边界条件法带入上式的有限元方程组式[15]，应用高斯消去法或者迭代法求解该方程组可得到场域各个离散网格点处的节点电位。

3　边界元法计算子域边界场强及内部节点场强

如图3所示的单介质子域是全场域的部分求解区域，该子域的介电常数εi为一定值，子域内部的电荷密度为ρi，子域边界Γi上的节点电位φi可从全域节点有限元法所计算的子域边界上的节点电位映射得到。

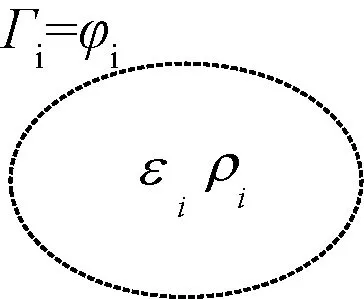
图3　单介质子域Fig.3　Single-medium subdomain

该子域的电位控制方程及边界条件如下所示：

(5)

根据格林定理：

(6)

式中:G为自有空间中的格林函数，满足2G=-δ，式中δ=δ(P,Q)为狄拉克函数；P，Q分别为场域中的场点及源点。在二维自由空间中的格林函数[16]为

(7)

式中：r为从源点到场点之间的距离。在三维自由空间中，格林函数为[16]

(8)

令ρi/εi=f，将子域电位控制方程式(3)带入格林公式式(4)中，结合格林函数的基本性质可以得到子域电位的边界积分方程为[17]

(9)

式中：在光滑边界上ci=1/2，场域内部ci=1，场域外部ci=0。φi为空间任意位置的电位，而式(9)右边的电位φ则表示子域边界上的电位。

对于子域边界上，式(9)中的φi以及φ均已给定，而∂φ/∂n为待求量。根据场强与电位的梯度关系，子域边界的法向场强为En=-∂φ/∂n，将其带入边界积分方程式(9)，此时将形成待求量为子域边界法向场强的边界积分方程。应用边界单元将子域边界离散成一系列的边界元单元，使用单元插值函数构造边界上电位φ以及边界法向场强En的近似值为

(10)

式中：n为子域边界节点总数；φj，En,j分别为节点电位以及节点表面法向场强。

将式(10)带入式(9)结合子域的边界电位通过配点的方式可以得到求解子域边界场强的离散代数方程组。

(11)

式中：e为离散边界单元编号；ne为离散边界单元的总数量；Gi为场点固定于第i个边界节点时的格林函数；δij为克罗内克函数(当场点i与源点j重合时其值为1，其余为0)，区域D为子域中含有电荷密度的区域。

将式(11)写成矩阵形式为

(12)

该式即为求解电位边界法向场强的矩阵方程。式中En为边界节点法向场强组成的向量，φ为边界节点电位组成的向量，A和B为与式(11)对应的系数矩阵。通过求解矩阵方程式(12)即可得到子域边界处的节点法向场强。对于子域边界处的切向节点场强可以通过边界电位的微分得到。子域内部任意位置的电位与节点场强可通过边界积分方程计算得到。

子域内部任意位置的节点电位可以通过全域有限元计算的节点电位映射插值得到，也可以通过式(9)的边界积分方程计算得到。子域内部求解电位的边界积分方程为

(13)

式中：φi为子域内部待求的节点电位。

根据电场强度与电位的梯度关系E=-φ，结合式(13)，可以得到求解子域内部节点场强分量的边界积分方程为

式中：ξ为空间坐标x，y，z的一个方向，即Eξ,i为内部节点i在ξ方向的电场强度的分量。

比较式(14)及式(15)可以看到采用边界元法计算的场域电位与场强具有相同的计算精度。使用边界单元离散子域边界，将边界电位及法向场强的插值公式(10)式带入(14)式可以得到计算子域内点的电场强度分量Eξ,i的计算方程式为

(15)

从上式可以看出计算子域内部任意位置的电场强度仅需要对子域的边界以及带有电荷源的区域进行网格剖分，并不需要对全部场域进行离散。计算子域某个内点的电场强度仅需要将该内点的空间坐标带入式(15)即可。与节点有限元法计算节点场强的方法相比，该方法灵活方便，而且计算效率更快。

4　算例分析

4.1计算模型及面积加权平均算法简介

本文采用一个场强具有解析解的双层介质同轴电缆模型，比较本文所提出的有限元―边界元混合算法与传统的面积加权平均算法求解节点场强的计算精度。同轴电缆的模型示意图如图4所示。

图4　双层介质同轴电缆模型Fig.4　Two-layer medium coaxial-cable model

图中所示的同轴电缆模型内半径R1=1 mm，介质分界面处的半径R2=2 mm，外半径R3=4 mm。介电常数ε1=ε0，ε2=5ε0。所加外电压为U0=100 V。该计算模型轴向场强的解析解为

(16)

式中：r为场域任意点与坐标原点的距离。

传统的求取场域节点场强的方法是对单元位函数直接进行数值微分，该方法不仅精度低而且由于一个节点与多个单元相连接使得连续介质中计算的节点场强也是多值的，这与实际物理规律相悖。面积加权平均算法计算节点场强的基本思路是对位函数进行数值微分取得单元重心处的场强，而节点场强则是与该节点相关联的单元重心处的场强的面积加权平均，其具体计算式为[18]

(17)

式中：Ek,i表示第i个节点k(k可为空间坐标方向x，y，z任一方向)方向的场强分量；Ne表示与节点i相关联的单元个数；Ek,eij表示与节点i相关联的第j个单元eij重心处k方向的场强分量；Seij为单元eij的面积。

4.2场域边界及介质分界面节点场强精度比较

首先，对图4所示的同轴电缆模型进行有限元网格划分求取节点电位以及运用面积加权平均法求取节点场强。网格划分单元采用四边形一次单元，场域网格数为7 200，节点数为7 320。接着，将场域按照介质类型划分成两个子域，然后对子域进行边界元计算子域的边界法向场强及子域内部节点场强。使用一次线性单元对子域边界进行边界网格划分，两个子域的网格数及节点数均为120。

在本模型的计算中，场强的大小仅与节点处的半径有关。应用有限元-边界元法(FBM)与面积加权平均法(AWA)计算模型边界及分界面处场强的大小以及误差分析结果如表1所示。表中位置r=1.00 mm处表示场域内表面边界处，r=2.00(-)表示分界面处偏向内表面一侧的位置，r=2.00(+)表示分界面处偏向外表面一侧的位置，r=4.00 mm处表示场域外表面边界处。从表中的计算结果可以看出，本文所提出的有限元―边界元混合算法计算场域边界及分界面处的场强大小误差均小于1%，计算精度较高。而面积加权平均算法在场域边界处的计算精度要比本文所提出的算法计算精度低，而在介质分界面处的计算结果与解析解相差很大，其主要原因是由于介质分界面处的法向场强不连续所导致的。

表1　场域边界及介质分界面处场强大小及误差分析

4.3场域内部节点场强精度分析

应用有限元-边界元法与面积加权平均法计算场域内部区域的节点场强，选取场域一条沿半径方向上的节点场强进行分析，选取的节点位置为距原点半径分别为r=1.20，1.50，1.80，2.50，3.00，3.50 mm的位置。选取节点所计算的场强大小及误差分析如表2所示。

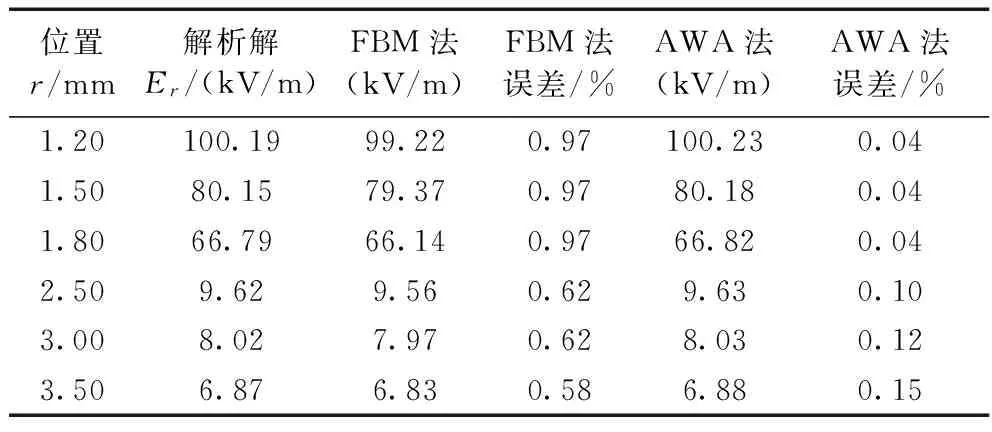
表2　沿半径方向场强大小及误差分析

表2中显示的计算结果表明对于子域内部节点场强的计算，传统的面积加权平均法与有限元-边界元计算误差均比较小，但是传统的面积加权平均法计算误差更小。实质上，这两种算法子域内部的计算误差可比性不大，原因在于面积加权平均法计算节点场强的精度与子域内部网格的剖分的密度有很大的关系。而有限元-边界元法计算子域内部的节点场强不需要对子域进行网格剖分，其计算精度与子域表面的节点法向场强和电位的计算精度以及数值积分的计算误差有关。

有限元-边界元法与面积加权平均法计算的节点场强沿半径方向的计算结果曲线图如图5所示。从这两种算法求解的电缆沿着半径方向场强大小的计算结果可以看出面积加权算法计算的场强大小在分界面处与解析解相差很大，计算值是介质分界面两边单元场强的面积加权平均，无法反映场强在介质分界面处不连续的特点。与此相比，有限元-边界元法求解场强的结算结果在场域边界、内部以及分界面处均与解析解一致，具有较高的计算精度。

图5　沿半径方向电场强度分布图Fig.5　Electrical field intensity along cable radius

5　结　论

本文提出了一种有限元边界元混合算法求解多介质静电场电场强度的计算方法。对一具有解析解的双层介质同轴电缆模型的电场进行了计算分析，可以得出以下结论：

(1)有限元边界元混合算法计算多介质节点场强可以很好地解决节点场强在分界面处法向场强不连续所引起的计算困难。算法在介质分界面及场域边界处的节点场强计算精度要比传统的面积加权平均算法高。

(2)应用边界元法计算子域内部场强，不需要再对子域内部进行网格划分。仅需要输入所计算点的空间坐标然后运用边界积分方程即可计算得到，比有限元法需要通过网格节点场强进行插值计算方便。

(3)本方法子域的划分仅需要满足单一介质的闭合区域条件即可。实际计算过程中可以仅对部分需要计算场强的区域提取子域信息，并不一定需要以介质分界面作为子域的边界，也可在单一介质内部划分子域，从而提高计算效率。

(4)本文仅对二维模型进行了算法验证，对于三维模型也可以利用本文所提出的算法进行计算。此外，对于其它类似的问题，例如多介质磁场问题也可以通过本文提出的算法进行计算。

[1] 崔翔, 谢羲. 计算电磁场量 E 和 B 的互补变分方法 [J]. 中国电机工程学报, 1988, 8(2): 22-32.

[2] 左鹏, 邹军, 袁建生. 三维有限元中提高由已知节点电位求场强计算精度的全域节点场强法 [J]. 中国电机工程学报, 2015, 35(5): 1243-1249.

[3] CAO W, ZHANG Z, ZOU Q. Superconvergence of discontinuous Galerkin methods for linear hyperbolic equations [J]. SIAM Journal on Numerical Analysis, 2014, 52(5): 2555-2573.

[4] SHI D Y, LI M H. Superconvergence analysis of the stable conforming rectangular mixed finite elements for the linear elasticity problem[J]. Journal of Computational Mathematics, 2014, 32(2): 205-214.

[5] ZHANG Z, NAGA A. A new finite element gradient recovery method: Superconvergence property [J]. SIAM Journal on Scientific Computing, 2005, 26(4): 1192-213.

[6] 张秀敏, 苑津莎, 徐永生, 等. 基于工程损耗模型的棱边有限元与节点有限元的算法比较 [J]. 电工技术学报, 2003, 18(3): 41-47.

[7] MUR G. Edge elements, their advantages and their disadvantages [J]. IEEE Transactions on Magnetics, 1994, 30(5): 3552-3557.

[8] 苑津莎, 张秀敏, 王志明. 棱边有限元法在工程涡流问题中的应用研究[J]. 华北电力大学学报, 2004, 31(3): 1-7.

[9] SIMPSON R N, BORDAS S P A, TREVELYAN J, et al. A two-dimensional isogeometric boundary element method for elastostatic analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 209: 87-100.

[10] LIU Y J, MUKHERJEE S, NISHIMURA N, et al. Recent advances and emerging applications of the boundary element method [J]. Applied Mechanics Reviews, 2011, 64(3): 1-38.

[11] 王泽忠, 赵良, 刘之方. 二维开域静电场有限元与边界元迭代解法的研究[J]. 华北电力大学学报, 2002, 29(z1): 36-40.

[12] 潘晓彤, 王泽忠, 方舟, 等. 直流输电换流阀系统表面电场分析与均压环设计[J]. 现代电力, 2014, 31(1): 68-73.

[13] REN Z, KALSCHEUER T, GREENHALGH S, et al. A hybrid boundary element-finite element approach to modeling plane wave 3D electromagnetic induction responses in the Earth[J]. Journal of Computational Physics, 2014, 258: 705-717.

[14] 倪成, 冯慈璋, 倪光正. 电磁能量和参数计算的互补和互补—对偶能量法[J]. 西安交通大学学报, 1986, 20(3): 91-101.

[15] 王泽忠. 简明电磁场数值计算 [M]. 北京：机械工业出版社, 2011:107-116.

[16] AIELLO G, ALFONZETTI S, BORZG, et al. Comparing FEM-BEM and FEM-DBCI for open-boundary electrostatic field problems [J]. The European Physical Journal Applied Physics, 2007, 39(2): 143-148.

[17] 吴洪潭. 边界元法在传热学中的应用 [M]. 北京：国防工业出版社, 2008:14-17.

[18] 倪光正, 杨仕友, 邱捷. 工程电磁场数值计算 [M]. 北京：机械工业出版社, 2010:140-148.

Finite Element Method-boundary Element Method for Calculation of Nodal Electric Field Intensity in Multi-medium Electric Field

XIE Yuqing, LI Lin

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206, China)

A finite element-boundary element hybrid method is proposed in this paper to solve the problem of inaccuracy when calculating the electric field intensity of field boundary and dielectric interface in the multi-medium electric field with nodal finite element method. Finite element method is firstly used to calculate the node electric potential of the field domain. Then, the whole domain is divided into several single-medium subdomains in which the boundary electric potential can be calculated by the mapping interpolation of node electric potential from the result of finite element method. Next, the boundary element method is used to calculate the normal field intensity at the boundaries in subdomains, and the interior electric field intensity will be calculated by boundary integral equation. The results show that such calculation method yields more accurate results when calculating the nodal electric field intensity of the field boundary and the interface than the traditional area-weighted average method, and the calculation error of the node intensity in the interior field is also of low level. The presented method could not only be used in the static electric field, but also can be used to solve calculation problems in other vector field with discontinuous field intensity in the dielectric interface.Key words：finite element method-boundary element method; multi-medium; dielectric interface; boundary electric field intensity

10.3969/j.ISSN.1007-2691.2016.04.04

2015-10-11.

国家自然科学基金资助项目(51277064)；中央高校基本科研业务费专项资金资助项目(JB2015131).

谢裕清(1991-)，男，博士研究生，主要研究方为电磁场数值计算及多物理场耦合计算；李琳(1962-)，男，教授，博士生导师，主要研究方向为电磁场理论及其应用和电力系统电磁兼容。

TM151

A

1007-2691(2016)04-0021-06