基于回热加热器变工况的机组热经济性通用数学模型
谭良红,胡三高,曹晟磊
(华北电力大学 能源动力与机械工程学院,北京 102206)
基于回热加热器变工况的机组热经济性通用数学模型
谭良红,胡三高,曹晟磊
(华北电力大学 能源动力与机械工程学院,北京 102206)
针对火电厂的回热系统,考虑外部热量引入时回热加热器变工况运行的影响,以汽轮机的功率方程、热力系统的热平衡方程、锅炉循环吸热方程为基础,经过严格的数学推导,导出纯热量引入回热系统时功率变化和吸热量变化的通用计算公式。以N300-16.5/550/550机组为例,计算在各级加热器引入1 kJ/kg纯热量的机组经济性变化,并与详细计算和等效焓降法计算的结果相比较,结果表明:和等效焓降法相比,在做功增量方面,除了一号加热器和除氧器,本方法计算的结果相对偏大,在吸热量方面也存在不同;而与详细计算的结果几乎一致,验证了本方法的正确性。
加热器;热经济性;热力系统;等效焓降法
0 引 言
汽轮机的回热系统是火电厂的主要组成部分,其参数的变化将对焓升分配造成影响,使得各段抽汽量发生变化,进而影响整个机组的经济性。为了阐释回热系统参数变化对机组经济性的影响,众多学者对回热系统进行了许多研究,研究的主要内容可以分为4类。第一类是等效焓降法,在主蒸汽流量不变的前提下,进行热力系统局部和全局的分析[1]。第二类矩阵分析法,文献[2-3]将热力系统中的变化视为扰动,建立了小扰动的分析理论;文献[4]在定功率的条件下,得出了热(汽)耗变换系数的分析方法;文献[5-6]完善了火电机组热经济性分析的物理模型和数学模型,并通过矩阵微分的理论,建立了多元扰动下的热力系统能效分析模型;第一类和第二类的基础均是热力学第一定律,而第三类的基础是热力学第二定律,文献[7]建立了热力系统的火用损分布的数学模型。第四类是针对具体参数变化的研究,文献[8-9],在回热加热器上、下端差变化时,对机组的热经济性进行了分析并建立了有关的数学模型;文献[10],利用微分的方法,求得了辅助汽水流量与机组煤耗的数学关系;文献[11]对高压加热器切除的情况进行了详细的分析并建立了热经济性变化的计算模型。以上理论分析都是在忽略了回热加热器变工况影响的前提下进行的,然而在较多外部热量引入回热系统时,采用以上方法研究时将存在误差,文献[12]考虑回热加热器变工况的影响,以137 MW机组为例,采用迭代的方法计算低温省煤器热量引入时的经济性变化,计算的结果和等效焓降计算的结果存在一定的误差。
针对外部热量并入回热系统,现有研究方法的结果不真实,本文为了准确计算外部热量引入对机组经济性的影响,在考虑外部热量引入对回热加热器变工况影响的前提下,以国产N300-16.5/550/550机组的热力系统为研究对象,利用严谨的数学方法,对外部热量对于热经济性影响的数学模型进行了推导,得到通用的数学计算模型。
1 热力系统热经济性的基本方程
N300-16.5/550/550回热系统如图1所示。
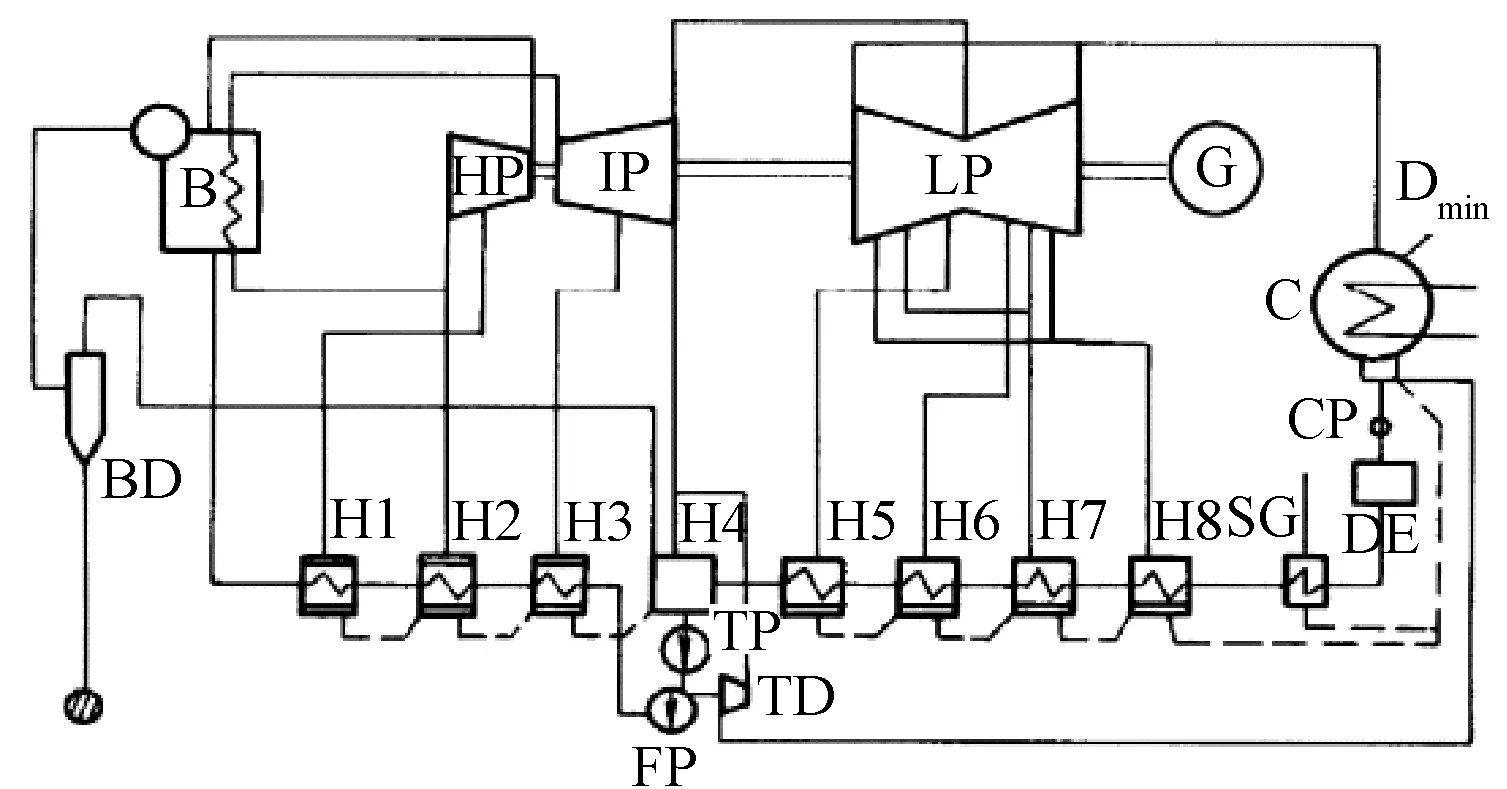
图1 N300-16.5/550/550回热系统Fig.1 Regenerative system of N300-16.5/550/550
1.1回热加热器的变工况
回热加热器主要的参数有:入口温度、出口温度、疏水温度和凝结水流量,各参数具有一定的相关性。外部热量的引入将会在一定程度上影响回热加热器的参数,例如:当外部热量通过并联的方式并入回热系统,将减少在该级回热加热器中的凝结水流量,而凝结水的出口温度将升高;当外部热量采用串联的方式并入回热系统,回热加热器的入口水温将会升高,出口温度也将升高。
回热加热器可以分为高压加热器、低压加热器以及除氧器,高压加热器换热面可以分为蒸汽冷却段、凝结段和疏水冷却段,如图2所示,而低压加热器可分为凝结段和疏水冷却段。通过各换热面变工况的分析,可得到回热加热器变工况的情况。

图2 三段式回热换热器示意图Fig.2 Schematic plot of three-stage regenerative heat exchanger
(1)疏水冷却段
疏水冷却段是利用进入回热加热器的凝结水冷却疏水,减少本级蒸汽的消耗增加了下一级蒸汽的利用。疏水冷却段正常运行时,其传热关系如下:
效能的关系式:
(1)
传热单元数的关系式:
(2)
凝结水和疏水采用的是逆流布置,效能和传热单元数有如下关系:
(3)

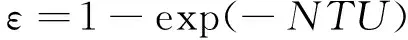
根据文献[14],疏水段的整体换热系数为
(4)
式中:εc为清洁系数;βm为管材修正系数;βt为给水温度修正系数;qm为凝结水流量。
变工况下整体换热系数为
式中:qm0为设计的凝结水流量。
其中给水温度修正系数[14]:
由以上分析可得变工况下传热单元数为
(5)
式中:NTU0为设计工况下的传热单元数。
由效能的定义式可得,疏水冷却段的凝结水出口温度为
(6)
根据疏水冷却段的能量守恒,疏水温度为
(7)
其中
(2)蒸汽凝结段
效仿HEI凝汽器的换热系数,蒸汽凝结段的整体换热系数为[13]
(8)
由于蒸汽凝结段有相变换热,因此效能的表达式为
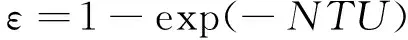
(9)
传热单元数为
(10)
凝结段凝结水出口温度:
(11)
(3)蒸汽冷却段
蒸汽冷却段的整体换热系数为[13]
(12)
传热单元数:
(13)
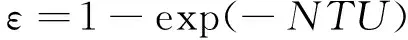
蒸汽冷却段的凝结水出口温度:
(14)
对于高压回热加热器,可由疏水冷却段、蒸汽凝结段以及蒸汽冷却段的变工况计算得到各参数的变化;对于低压加热器,则可由疏水冷却段和蒸汽凝结段的变工况计算得到各参数的变化。
1.2热平衡方程、功率方程和吸热量方程
根据文献[15],图(1)所示的热力系统,其热平衡方程可以写成如下:
(15)
式中:A为回热系统的结构矩阵;Af是轴封漏汽的结构矩阵;Aτ代表辅助水的结构矩阵;αj是回热抽汽系数;αfj代表轴封漏汽流量系数;ατj是辅助水的流量系数;Δqj代表进出加热器的纯热量;τj代表加热器的给水焓升。
文献[15],功率方程如下:
(16)
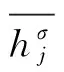
文献[15],锅炉的循环吸热量:
(17)
式中:αzr为再热蒸汽的份额。
1.3补充方程
由于考虑外部热量对于回热参数的影响,需要补充一些方程,以低温省煤器串联回热系统为例,如图(3)所示,外部纯热量串联于i+1级加热器的出口,补充方程如下:
i+1级加热器出口焓值:
(18)

对于i级加热器,由于凝结水的入口焓值提高,凝结水的出口焓值和疏水焓值也将提高。由回热加热器变工况的分析,可知出口焓值和疏水焓值是凝结水水量和入口焓值的函数。
(19)
(20)
对于除氧器,因为其是汇集式加热器,出口温度只和抽汽的压力有关。
(21)

图3 外部热量串联于回热系统示意图Fig.3 Schematic plot of the series of external heat and regenerative system
2 外部热量对汽轮机热经济影响的计算模型
2.1抽汽量的变化
对机组经济性的研究,主要分为两种,定流量和定功率,本文计算模型的推导是以定流量的情况为例进行推导的。
对热平衡方程进行求偏导:
忽略辅助水和轴封漏汽的变化,则
原式简化为
对各级加热器焓升求偏导:
(22)
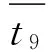
对于各级加热器出口焓值进行求偏导,分3种情况:
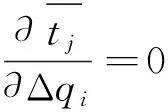
由于除氧器是汇集式加热器,其出口温度只和抽汽压力有关,所以低压加热器出口焓值的变化不会对除氧器出口焓值产生影响。
对外部纯热量向量求偏导,当且仅当j=i+1时,偏导数为1,其他的偏导数为0。
对于结构矩阵进行求偏导:
(23)
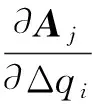
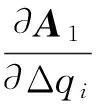

对于各级回热加热器的疏水焓值求偏导,同样也存在3种情况:
由以上分析可得,在i级回热加热器入口串联部分纯热量,其抽汽量的变化:
(24)
2.2做功量和吸热量的变化
本文主要考虑在外部热量引入时,回热系统参数变化所造成的经济性变化,忽略主蒸汽焓值、排汽焓值、再热吸热量和轴封漏汽做功量的变化,则功率变化量为
(25)
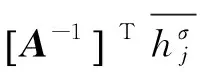
则在i级加热器入口处以串联方式引入纯热量,所造成机组功率的增量为
(26)
若忽略外部热量的引入对回热加热器变工况的影响,右式中的第一项和第二项为零,则上式与等效焓降的计算公式相同,可见等效焓降是通用计算模型中的特殊情况。
在有外部热量引入时,锅炉的循环吸热量变量为
(27)
将式(24)代入上式,得到循环吸热量的变化。
2.3机组热经济性的变化
机组的热效率:
(28)
外部热量引入之后,热效率为
(29)
热效率的绝对变化:
(30)
热效率的相对变化为
(31)
采用以上的计算方法,对任意的热力系统,可以计算回热加热器变工况所造成的做功量和吸热量的变化,进而求得机组经济性的变化。
2.4不同外部热量引入方式
以上分析都是针对外部热量采用串联的方式并入回热系统,但是在实际工程中,电厂有采用并联的方式并入回热系统。对于此种情况应该将其转化为串联的方式来计算其经济性。下面以低温省煤器并联6号和7号回热加热器的情况进行分析,如图4、图5所示。
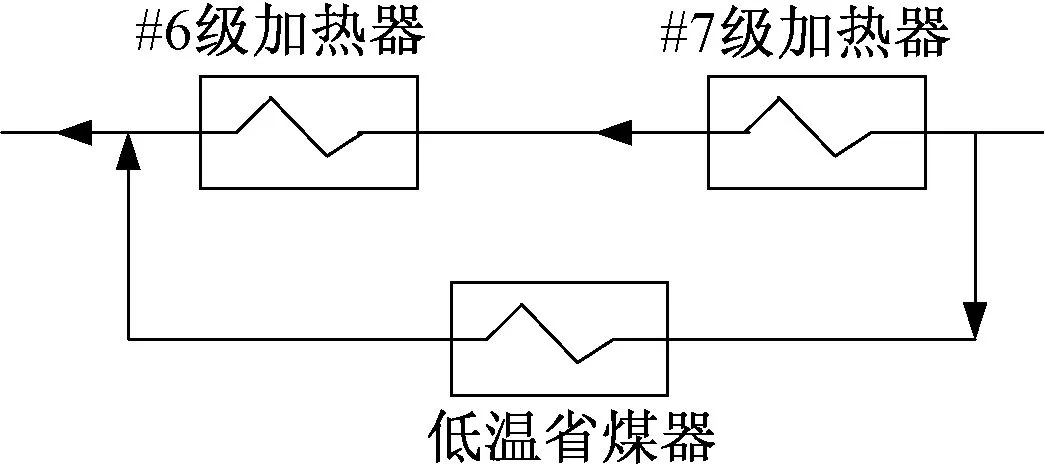
图4 外部热量并联入回热系统示意图Fig.4 Schematic plot of parallel of external heat and regenerative system
当从回热系统引出一部分凝结水用于吸收外部热量,回热加热器中的凝结水流量减少,通过回热加热器变工况的分析,可以计算回热加热器的出口焓值。
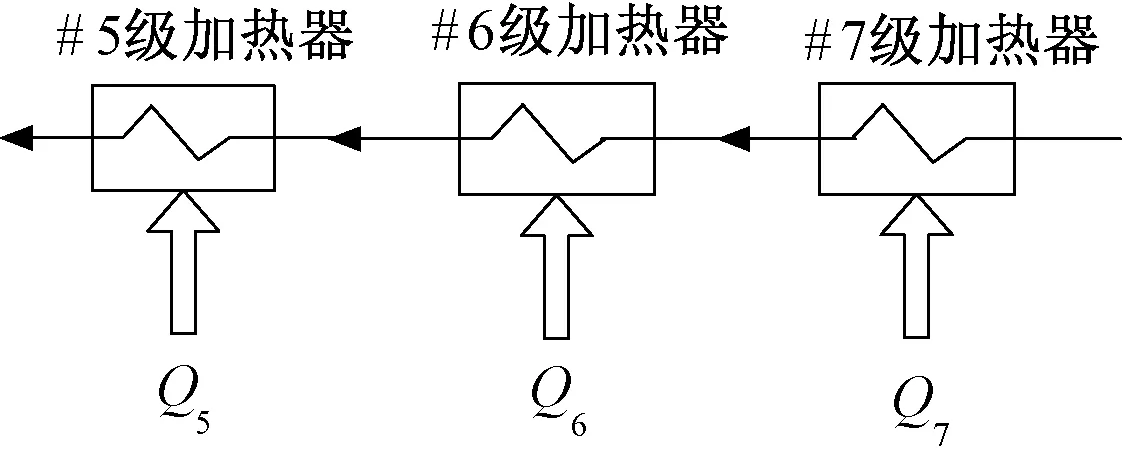
图5 并联连接方式示意图Fig.5 Schematic plot of parallel connection
7号加热器的所吸收的外部热量为
6号器所吸收的外部热量为
5号加热器所吸收的外部热量为
根据如上分析,将并联方式转化为串联方式,清楚的显示各级加热器的吸热量,根据串联方式热经济性的计算各级热量的热经济性变化。
做功量的变化值:ΔN=ΔN7+ΔN6+ΔN5
循环吸热量的变化值:Δq=q7+q6+q5。
3 实例计算
以图1所示的N300-16.5/550/550的机组为例,在各级加热器入口分别引入纯热量1 kJ/kg,则这部分热量将造成回热加热器变工况,根据回热加热器变工况的分析,以一阶偏导在设计参数时的导数近似的表示各参数的相对变化量,计算的结果如表1所示。

表1 各参数的在设计参数下的偏导数
由表1可知入口焓值、疏水焓值以及出口焓值的相对变化,对于入口焓值,由于1号、2号以及3号加热器中的凝结水流量和新蒸汽流量相同,因此相对变化量为1 kJ/kJ,而除氧器、5号至8号加热器中入口的凝结水流量只为总流量的76%,因此相对变化量为1.32 kJ/kJ;对于疏水焓值,除了除氧器,其他加热器的疏水焓值随着入口焓值的提高均有较大的提高;对于出口焓值,除氧器的出口焓值只与抽汽压力有关,因此不发生变化,而其他加热器的出口焓值随着入口焓值有小范围的提高,其中高压加热器出口焓值受入口焓值的影响较小;外部所引入的热量主要分为三部分,大部分的热量在本级被利用,还有一部分热量由于出口焓值的升高在高一级得到利用,剩下的热量伴随着疏水在下一级加热器中得到利用。
分别利用本方法、等效焓降法以及详细算法计算在各回热加热器入口引入1 kJ/kg纯热量时机组热经济性的变化,计算的结果如表2所示。
对于本方法和等效焓降法,由于本方法考虑了回热加热器变工况的影响,故两种方法在做功增量和吸热量增量方面存在一定的差别。在做功增量方面,考虑引入外部热量后加热器进口焓值、疏水焓值和出口焓值的变化,除了1号加热器和除氧器,本方法计算的结果相对偏大;对于1号加热器,由于出口焓值的提高,在1号加热器中被利用的热量减少,相比于等效焓降法,第一段抽汽的排挤相对减少,做功增量偏小;对于除氧器,出口焓值和疏水焓值是抽汽压力的单值函数,因此两种方法计算的做功增量相同;对于8号加热器,由于疏水流量较大并且疏水的热量在凝汽器中释放没有产生功,在一定程度上抵消了做功的增量,因此两种方法计算的结果相差很小;对于其他回热加热器,随着疏水量的增加,被下一级加热器利用的热量增多,抵消了部分高一级加热器的做功增量,因此随着疏水量的增多,两种方法的差异也在减小,如表2所示,在高压段,差值由2号加热器的0.010 8 kJ/kg降低到3号加热器的0.005 6 kJ/kg,而在低压段,差值由5号加热器的0.011 6 kJ/kg逐步降低到8号加热器的0.001 0 kJ/kg。在循环吸热量方面,对于在3号加热器入口引入外部热量的情况,3号加热器出口焓值升高导致第二段抽汽减少,再热份额增加,因此相比于等效焓降法,循环吸热量增量大于零;对于2号加热器,2号加热器出口焓值升高减少了第一段的抽汽,但是第一段抽汽的放热量大于第二段抽汽,总的再热份额增大,因此循环吸热量增量大于等效焓降法的结果;对于1号加热器,引入外部热量也会提高出口焓值,相比于等效焓降法,第一段抽汽量将增多,同时给水温度升高,因此减少了锅炉的吸热量。
对于本方法和详细计算,不管是在做功增量还是循环吸热量方面,两种方法计算的结果几乎一致,证明了本方法证明本方法计算的正确性,因此对于外部热量以串联方式并入回热系统的情况,可以采用本方法更为准确的计算机组的经济性变化。
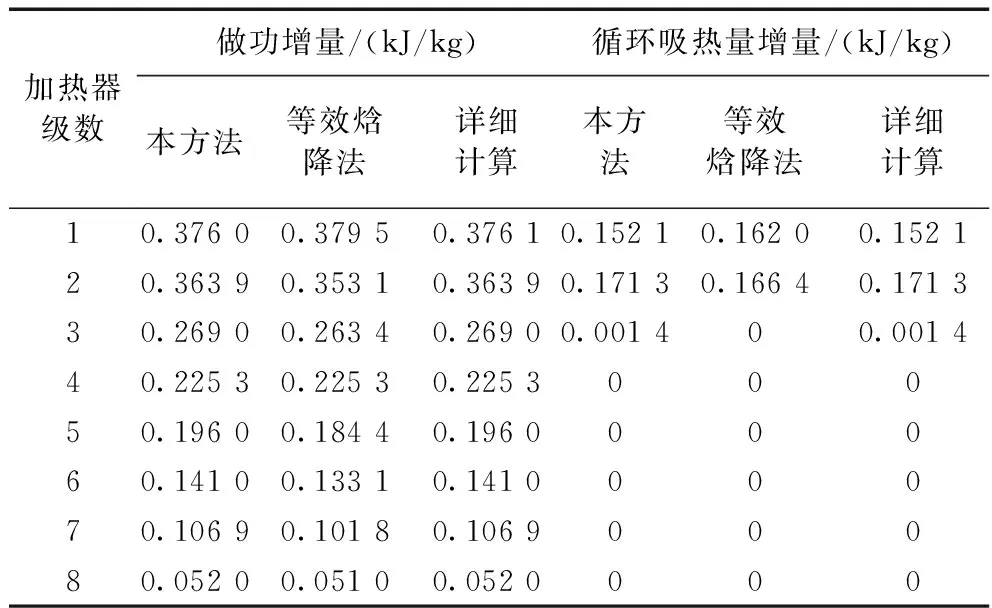
表2 纯热量串联引入时热经济性变化
4 结 论
考虑外部热量引入时回热加热器变工况的影响因素,对回热加热器的变工况进行了较为细致的分析,经过严格的数学推导,导出纯热量引入回热系统时功率变化和吸热量变化的通用计算公式,完善了回热系统经济性的计算模型。以实际机组为例,分别计算在各级加热器入口引入1kJ/kg纯热量所造成的热经济性变化,并与等效焓降法和详细计算的结果进行比较,结果表明:在做功量方面,相比于等效焓降法计算的结果,除了1号加热器和除氧器,本方法计算的结果偏大;在循环吸热量方面,对应于3号加热器的循环吸热量增量不为零,对应1号加热器的吸热量增量偏小,而2号加热器的吸热量偏大;本方法计算的结果几乎和详细计算的结果相同,验证了本方法计算结果的正确性,因此可以采用本方法对外部热量引入时机组经济性变化进行细致的计算。
[1] 林万超. 火电厂热系统节能理论[M].西安:西安交通大学出版社,1994.
[2] 昌晶,张春发,田红景. 小扰动理论及其在电厂热经济性分析中的应用[J]. 节能技术,2006,24(3):250-252.
[3] 张春发,郭民臣. 电厂热力系统分析中的两个重要参量[J]. 工程热物理学报,1993,14(4):365-368.
[4] 郭民臣,王清照,魏楠,等. 热(汽)耗变换系数法——分析电厂热力系统的新方法[J]. 中国电机工程学报,1997,17(4):12-14.
[5] 刘扬. 多元扰动下的热力系统能效预测研究[D].保定:华北电力大学,2013.
[6] 梁明仁. 大型火电机组能效预测软件开发[D].保定:华北电力大学,2014.
[7] 葛斌,张俊礼,殷戈. 火电机组热力系统与设备用损分布通用矩阵模型[J]. 东南大学学报(自然科学版),2009,39(5):1043-1048.
[8] 闫顺林,刘志巍,滕龙,等. 加热器上端差对机组能效影响的分析研究[J]. 汽轮机技术,2014,56(5):379 -381.
[9] 张学镭,王松岭,陈海平,等. 加热器端差对机组热经济性影响的通用计算模型[J]. 中国电机工程学报,2005,25(4):168-173.
[10] 李永华,闫顺林,王松岭. 煤耗与辅助汽水流量的通用微分关系式[J]. 中国电机工程学报,2001,21(11):80-84.
[11] 李飞飞. 切除高压加热器对汽轮机性能影响探讨[J]. 山东工业技术,2015,(15):187.
[12] 黄新元,平亚明,孙奉仲. 火力发电厂低压省煤器系统的最佳水量分配[J]. 水动力学研究与进展(A辑),2003,18(5):526-531.
[13] 闫水保,徐治皋,周振华,等.回热加热器正常状态的确定[J].电站系统工程,2001,17(5):283-284,297.
[14] 卢国栋,张春发,孙燕,等.带蒸汽冷却段的加热器端差基准值变工况特性研究[J].汽轮机技术,2008,50(2):126-127,130.
[15] 闫顺林. 多元扰动下的热力系统能效分析模型及应用研究[D].北京:北京华北电力大学,2011.
General Mathematical Model for Heat Economy of Unit Based on Operation Condition of Regenerative Heater
TAN Lianghong,HU Sangao,CAO Shenglei
(School of Energy Power and Mechanical Engineering, North China Electric Power University, Beijing 102206, China)
The general calculation formula of power change and heat change are found through strict mathematical derivation to the regenerative system in plant, considering the operation of regenerative heater for external heat, based on heat balance equation, turbine power equation and boiler absorbed heat equation. When 1 kJ/kg heat is introduced to every level of the heater in a N300-16.5/550/550 unit, the change of heat economy is calculated and the result is compared with that of the detailed calculation and the equivalent enthalpy drop method, and the result shows: in terms of incremental doing work, the result of this method is bigger than that of equivalent enthalpy drop method except the first heater and deaerator, and there are also some differences in the change of heat; the result of the detailed calculation is consistent with that of this method, which verifies the rightness of this method.
heater; heat economy; thermodynamic system; equivalent enthalpy drop method
10.3969/j.ISSN.1007-2691.2016.04.16
2015-10-08.
谭良红(1990-),男,硕士研究生,主要研究方向为火电厂节能。
TP323
A
1007-2691(2016)04-0104-07

