计及分布式电源的改进配网潮流计算方法

梁　宵，焦彦军，蒋晨阳

(华北电力大学 电气与电子工程学院, 河北 保定 071003)



计及分布式电源的改进配网潮流计算方法

梁宵，焦彦军，蒋晨阳

(华北电力大学 电气与电子工程学院, 河北 保定 071003)

针对多节点形式分布式电源并入配电网后导致传统潮流计算方法并不适用的问题，对牛顿潮流计算方法进行改进，提出每次迭代时结合梯度下降法与牛顿法对雅克比矩阵中各元素进行优化。改进算法解决了配网中由于分布式电源节点类型丰富导致传统算法计算困难的问题，同时，也解决了由于配网线路阻抗比值较大导致雅克比矩阵收敛困难的问题。根据改进算法提出以零阻抗连接编号方案为基础的潮流计算流程。通过数学理论分析与IEEE33节点仿真验证，改进算法在收敛性、收敛速度等方面较传统方法均有所提高。经由验证结果表明，改进算法适用范围较广，对于含分布式电源的配网快速潮流分析与实时调度计算提供有效的参考。

分布式电源；配网潮流计算；雅克比矩阵；改进算法；零阻抗连接编号

0　引　言

受环境问题、未来能源问题和电力体制改革等综合因素的影响，分布式电源(Distributed Generation, DG)近年成为研究热点。分布式电源是指在配电系统靠近用户侧引入的功率为数千瓦至50 MW的小型模块式、与环境兼容的独立电源，具有投资少、占地小、建设周期短、节能、环保等特点[1-2]。分布式电源并网后，改变原配电网单端电源辐射型网络为多电源网络，从而改变潮流方向[3-4]。因此，亟需在保证收敛性前提下，得到计算速度快的新潮流计算方法，满足含分布式电源配电网中分析和调度的需要。

目前常见的分布式发电并网系统有微型燃气轮机并网系统、风力发电系统、燃料电池与光伏并网发电系统[5-8]。对于微型燃气轮机并网系统根据并网PWM变流器类型分为电流型与电压型，对于电流型并网系统其节点类型为PI节点；而对于电压型并网系统，其节点类型由运行模式决定，联网模式下为PV节点，孤岛模式下则为VQ节点。风力发电系统以异步电机直接并网发电系统和双馈发电系统较为常见，其节点形式与其运行方式及控制策略有关。异步电机节点发出的有功功率确定，无功功率则与机端电压有关，称该类电源节点为电压静特性节点，表示为P-Q(V)；双馈发电系统一般采用恒功率因数控制方式，因此节点类型为PQ节点。对于燃料电池的输出控制与常规发电机控制原理近似，故在潮流计算中，燃料电池发电站并网节点可作为PV节点处理。光伏并网发电系统的节点类型同样受并网逆变器类型决定，对于电流型逆变器其节点类型为PI节点；而电压型节点类型为PV节点。

传统配电网的潮流算法有前推回代法、回路阻抗法、牛顿法和Zbus高斯法，具体算法参考文献[9-12]。传统潮流计算方法适用节点类型有限，对于分布式电源的节点类型并不适用。文献[13]对前推回代法进行改进，以节点电抗矩阵形式将PV节点转化为PQ节点，对于无功初值的确定，提出无功分摊原理，提高了计算速度。文献[14]从分布式电源的数学模型出发，着重分析风机并网后，对雅克比矩阵的影响，引入参数修正雅克比矩阵。该方法可以有效解决风机并网后传统牛顿法的问题，但是，由于并未考虑其他分布式电源并网形式，局限性较强。文献[15]以回路分析法为基础，利用配电网相角相差不大的特点将回路方程化简为线性代数方程。该方法在较为简单的配电网中适用性较强，但随着网络拓扑复杂度的不断提升收敛速度明显降低。

多节点类型的分布式电源经数次迭代后均可转化成PQ、PV节点[16]，目前，对于无分布式电源并网的配网广泛应用的前推回代潮流计算方法主要处理PQ节点，不适用于含PV节点的潮流计算中，同时，该方法的收敛速度随着网络规模的扩大而降低。牛顿法潮流计算在处理PQ、PV节点理论上较为成熟，且迭代次数于网络规模无关。影响牛顿法在配电网潮流计算的主要问题是在配电网中电阻电抗比值较大使雅克比矩阵收敛困难，较易出现“病态”潮流。

针对上述问题，本文提出每次迭代时梯度下降法与牛顿法相结合对雅克比矩阵元素进行调整，解决牛顿法在配网潮流计算中收敛困难的问题。通过数学理论分析与IEEE33节点实例仿真对比改进算法与传统算法的收敛性，收敛速度等问题，验证改进算法适用于多分布式电源并网的配网潮流计算中。

1　改进潮流算法数学模型

1.1数学模型

牛顿法潮流计算的基本思路[17]是将潮流方程F(X)=0用泰勒级数展开，在初始值接近于真值的前提下，略去二阶项以及更高次项，将非线性方程逐次线性化，反复形成并求解修正方程。直角坐标下修正方程为

(1)

式中：X和ΔX分别表示n个状态变量和其修正量组成的n维列向量；F(X)是由n个函数组成的n维列向量；J为n阶雅克比矩阵，第i行第j列元素Jij=∂fi/∂xj，角标k表示第k次迭代。

由上式可知，雅克比矩阵是潮流计算的关键，因此，对雅克比矩阵的修正计算是解决牛顿法收敛性问题的根源。在初值与真值相差较大的条件下，将非线性方程逐次线性化的过程中，牛拉法迭代收敛困难，为避免该问题的发生，利用非单调搜索准则，现将式(1)改进为

(2)

式中：μ为迭代参数；I为与雅克比矩阵J同阶单位阵。

该方法主旨是将梯度下降法与牛顿法的算法优缺点互补，从而达到高效结合。从式(2)中可以看出，若迭代参数μ(k)接近于1，此时为梯度下降法，若迭代参数μ(k)=0，则转变为牛顿法。梯度下降法在迭代过程中下降速度较快，对于收敛速度的改善有很大帮助，但在最优值附近继续迭代时，由于下降梯度趋于零，导致收敛速度减缓；而牛顿法在最优解附近依然能够产生一个理想的搜索方向，弥补了梯度下降法的不足。通过将上述方法的有效结合，克服了雅克比矩阵J几乎奇异或坏条件时牛顿法所带来的收敛困难，提高了收敛速度。

初始μ(0)赋值较大，则可向着残余平方和急剧下降的方向进行，在迭代的过程中，如果F(X(k))递增则说明迭代过程是发散的，此时μ(k)应增加，使F(X(k))向着递减的方向进行。随着迭代次数的不断增加，越趋近于最优解，μ(k)值应逐渐减小，有效避免提前进入局部最优解。

对于每次迭代μ(k)值的选取与实际减少速度Ared和预测减少速度Pred有关。定义：

实际减少速度表达式为

(3)

预测减少速度表达式为

(4)

两者的比值为

(5)

当比值ρ(k)接近于1时，说明线性模型比较准确，当比值ρ(k)接近于0或负值时，说明迭代次数过多，以至线性化出现无效。故：

(6)

1.2收敛性证明

设潮流方程F(X)=0解收敛于X*，雅克比矩阵的奇异值分解结果表示如下：

(7)

式中：

迭代过程中，中间迭代解X(k)所对应的雅克比矩阵奇异值分解为

(8)

由J(k)的奇异值分解结果可知当前的迭代值为

(9)

且

(10)

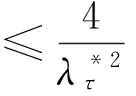
(11)

(12)

根据式(9)～(12)可得

(13)

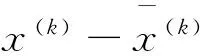
(14)

故

(15)

因此，X(k)二次收敛于方程组的解，即该算法具有二阶收敛性，优于只具备一阶收敛性的牛顿法。

2　含分布式电源的改进算法的实现

2.1节点编号方案

对于多节点类型分布式电源并网的配网节点编号采用断点零阻抗连接的编号方案。在编号时，首先忽略所有分布式电源，从始端节点依次向末端节点编号1,2,…,N，分布式电源从N+1开始编号，看作独立的节点，通过一条具有零阻抗的线路与配电网相连。如图1所示，原配电网标号为0-11，分布式电源通过一条零阻抗线路在节点3出并网，编号为12。

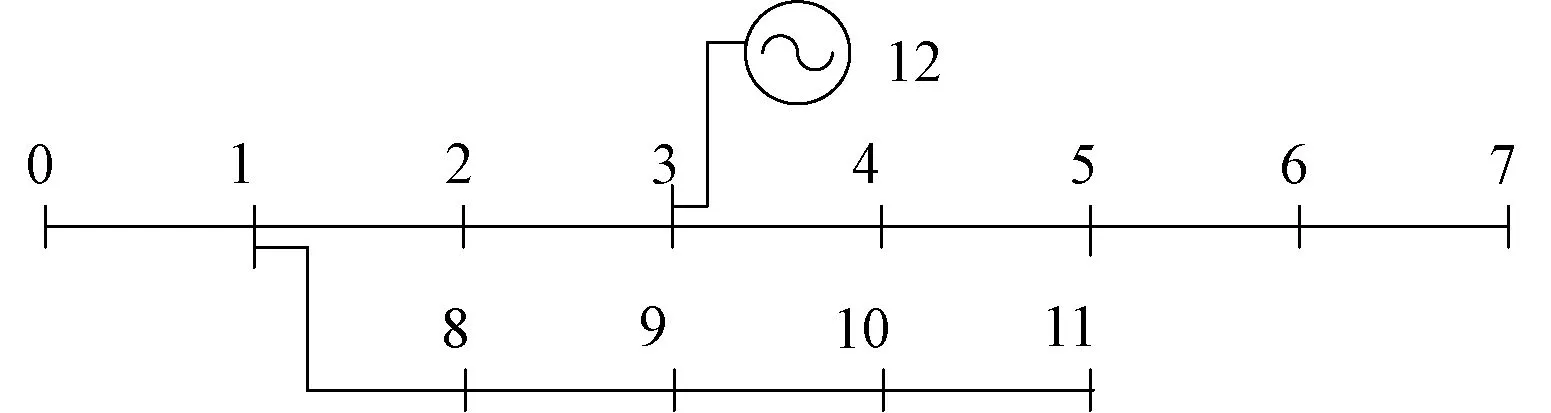
图1　简单含分布式电源配电网络图Fig.1　Simple distribution network with DG

该方法保证了原配电网络编号的完整性，分布式电源并网并不影响原网络编号，并网点的随机选择性增强，对于程序修改较为便捷。

2.2改进算法实现步骤

为确保潮流计算的可行性，作出以下假设：

(1)为保证整个配网是严格吸收型网络，限制分布式电源并网总容量，即负荷总容量大于分布式电源总容量。

(2)分布在不同馈线上的负荷为恒功率负荷。

规定流入节点功率为正，流出节点功率为负。多节点类型分布式电源并网的配网潮流计算步骤如下：

①节点编号

对于多节点类型分布式电源并网的配网节点编号按照2.1中阐述的断点零阻抗连接的编号方案进行。

②输入原始数据和信息

(a)输入支路阻抗数据；

(b)确定分布式电源节点类型；

(c)输入负荷注入的有功和无功;(d)输入平衡节点的电压

根据引言部分对常见并网分布式单元的节点类型的介绍，控制方式与运行模式决定了常见分布式电源的节点类型，主要为PQ节点、PV节点、PI节点以及P-Q(V)节点4种类型。各类型节点已知的基本信息以及在潮流计算前的初值设定如表1所示。

表1　分布式电源各类型节点基本信息及初值设定

(3)设定迭代参数μ0初值以及计算精度ε

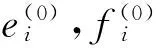
(5)若max(ΔP(k),ΔQ(k),ΔV(k)2)≤ε，停止计算；否则，计算：

(16)

(6)根据式(3)～(5)计算Ared(k)、Pred(k)、ρ(k)

(7)根据式(6)更新μk，返回第(5)步。

3　算例验证

为验证算法的有效性与收敛性，在VC++6.0环境下进行编译仿真，设计如下2组仿真实验。

实验1：在不含分布式电源的配网系统中，分别采用本文改进算法与其他传统潮流计算对同一网络进行潮流计算，并从收敛速度与收敛精度等方面进行比较。

实验2：验证算法在含分布式潮流计算中的实用性。对给定节点安装分布式电源并采用本文算法进行潮流计算，验证算法在单一节点并网与多节点并网中的实用性，并分析不同节点类型的分布式电源并网后对配网的影响。

3.1系统基本资料

本文以IEEE33节点[18]为算法验证系统，为便于计算，采用标幺值，设定基准值VΒ=12.66kV，SΒ=10 000kVA。系统拓扑图如图2所示。

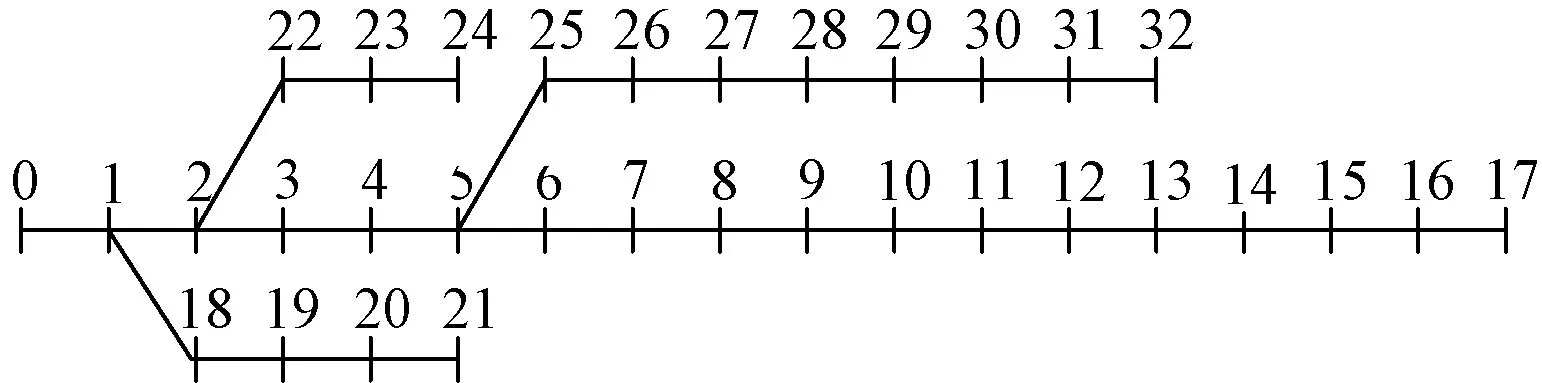
图2　IEEE 33节点网络拓扑图Fig.2　IEEE 33-node test system

3.2计算结果与分析

(一)实验1计算结果与分析

由于牛顿法在潮流计算中不适用于电阻电抗比值较大的网络中，该网络所形成的雅克比矩阵不易收敛。故与配网常用的前推回代法计算结果相比较，从而验证本文提出算法在收敛性与收敛速度的优越性。实验1计算结果如图2所示。

表2　各节点电压实际值与计算值

两种算法结果误差统计见表3。通过与参考值[19]相比较的误差结果可知，改进算法与实际值更为接近，误差率低，更适用于配电网的潮流计算中。

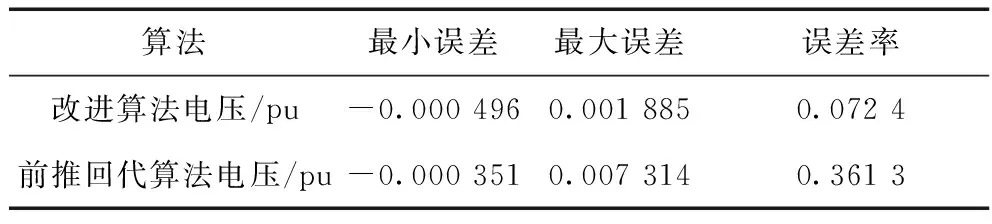
表3　两种算法结果误差统计

两种算法计算时间见表4。由表中数据可知，本文算法大大缩短了计算时间，提高了计算速度。在大规模配电网潮流计算时，本文所提出的算法对于快速潮流分析与实时调度计算更加适合。

表4　两种算法计算时间比较

(二)实验2计算结果与分析

为验证算法在含分布式潮流计算中的实用性，设定分布式电源并网点与参数类型如表5所示，由于P-Q(V)型分布式电源根据给定函数关系在求出无功功率后即可视为PQ型DG，不具备特殊性，故在此不再专门设置P-Q(V)型节点。

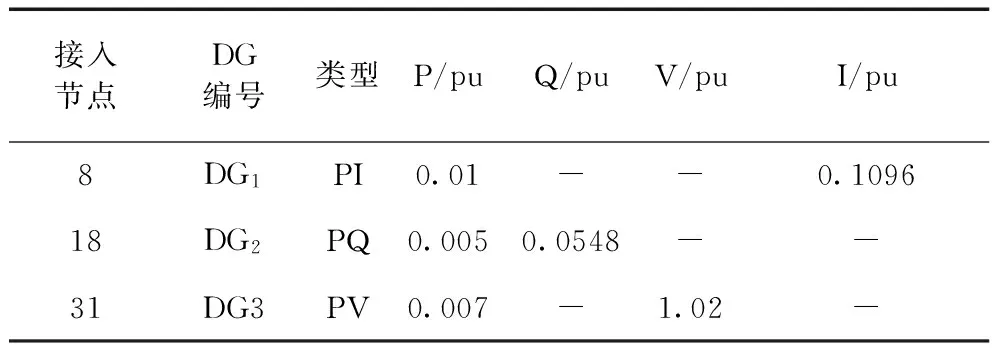
表5　分布式电源基本资料

(1)单一分布式电源并网

令DG1、DG2、DG3分别在相应并网点并入电网，通过改进算法进行计算，单一分布式电源并网后迭代次数与迭代时间如表6所示。

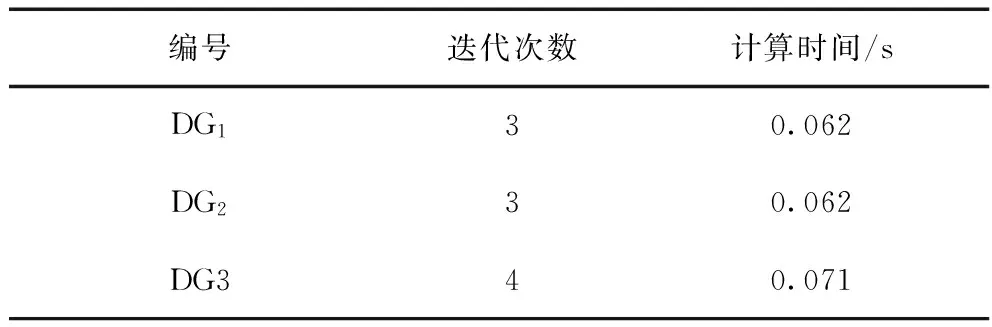
表6　单一分布式电源并网潮流计算迭代次数与计算时间

由表6数据可知，不同类型分布式电源并网后潮流计算迭代次数与并网前迭代次数相差不大，由此说明改进算法在潮流计算过程中的迭代次数与网络规模相关性较弱。同时，计算时间仍较传统算法时间短，说明改进算法在单一分布式电源并网潮流计算中能够提高收敛速度，大大缩短计算时间。

通过潮流计算可知不同情况下各节点电压分布情况如图3所示。

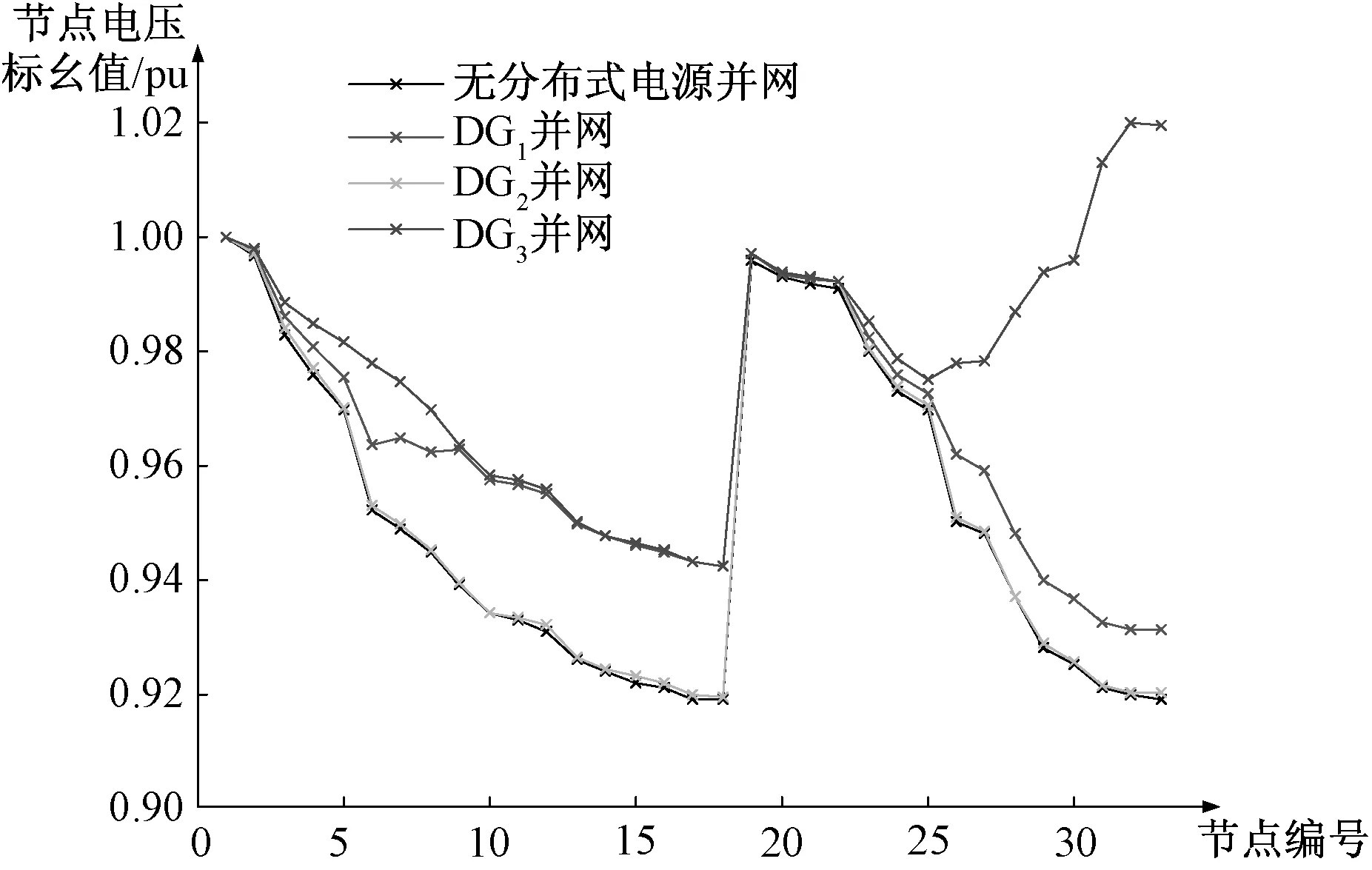
图3　DG并网后与并网前各节点电压Fig.3　The voltage before and after DGs connected

由图3中电压分布情况可知，PI、PQ型DG并网提高了并网点的电压，同时也提高了所在支路的电压，其容量越大提高幅度越明显，但对于相邻线路电压的改善并不明显；PV型DG为保证所在节点的电压稳定，同样对相邻节点电压有提升的作用，同时对所在支路电压的提升也有贡献。

(2)多种分布式电源并网

根据表5中分布式电源基本资料将DG1、 DG2与DG3分别于节点8、18、31同时并网，通过改进算法所得各节点电压分布情况如图4所示。

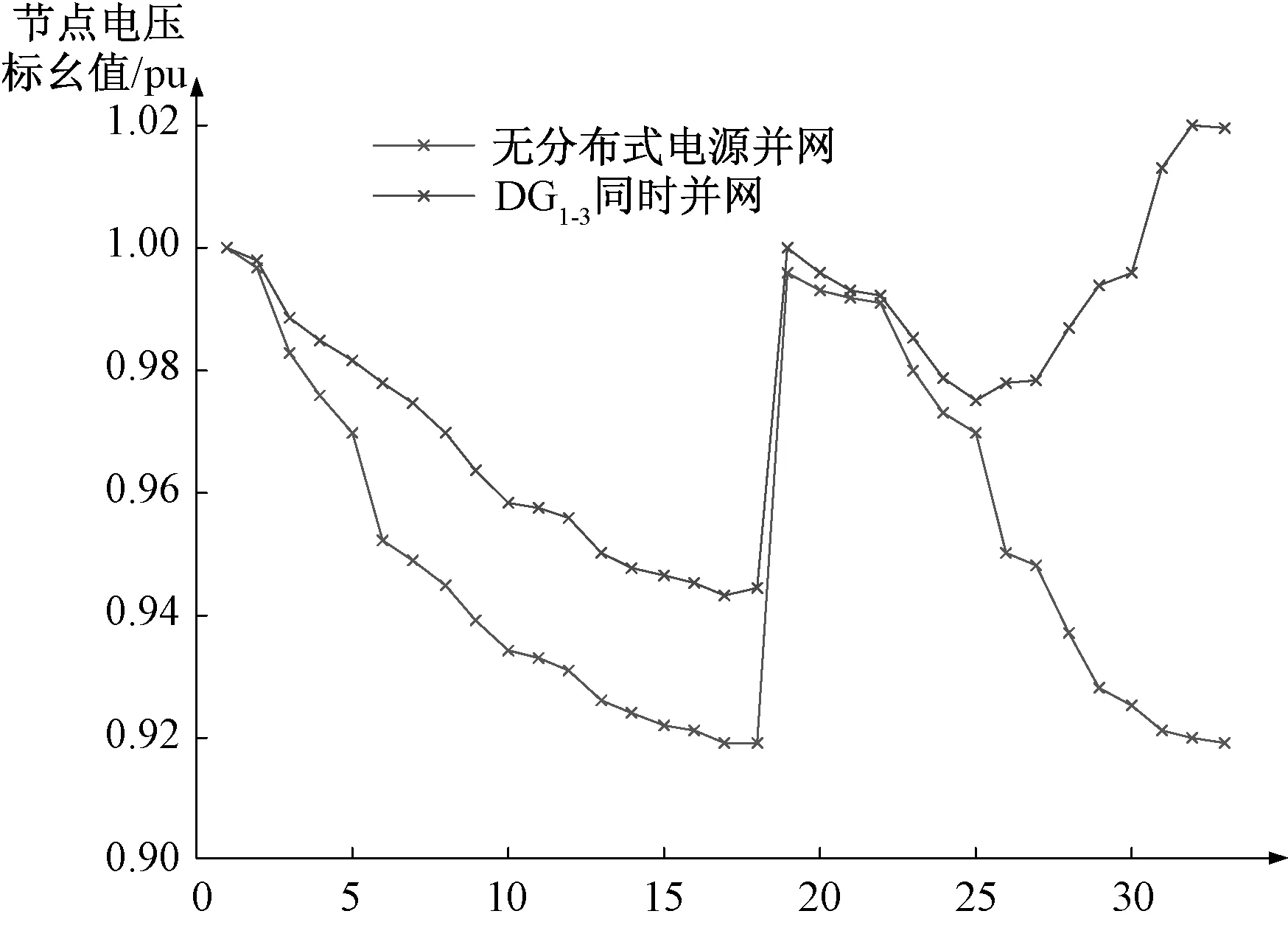
图4　DG1-3并网后与并网前各节点电压Fig.4　The voltage before and after DG1-3 connected

潮流计算中迭代次数为7次，计算时间为0.086 s。说明随着分布式电源并网数目的不断增多，类型不断丰富，其迭代次数与计算时间也会随之相应提高，但仍较传统算法计算速度快。由图可知，随着配网中多节点类型的分布式电源广泛接入，对各节点电压均有较为明显的改善。

4　结　论

由于DG类型众多，在潮流计算中如何正确考虑其节点类型是问题的关键。本文以配电网常见并网分布式电源系统为背景，分析传统配网潮流计算方法不足之处，考虑配电网电阻电抗比值较大的实际问题，对牛顿法进行改进，提出在每次迭代时对雅克比矩阵元素进行修正，在保证收敛性的前提下提高收敛速度，通过理论推导与仿真验证得到以下结论：

(1)改进算法在对配电网潮流计算中从准确性、收敛性以及计算时间上均优于传统算法。同时，该方法有效解决了配网中电阻电抗比值较大导致修正方程收敛困难的问题。

(2)本文提出的算法可有效地对多节点类型分布式电源并网的配网进行潮流计算。不仅适用于单节点并网，同样适用于多种分布式电源并网。该算法兼具牛顿法与梯度法的特点，如迭代次数与网络规模无关，计算速度快等等。对于单一分布式电源并网的潮流计算，其DG类型对于计算的迭代次数与迭代时间影响不大，与传统潮流计算方法相较有大幅提高。然而随着分布式电源并网数目的不断增多，类型不断丰富，其迭代次数与计算时间也会随之相应提高，但仍较传统算法计算速度快。

[1] 谷彩连,冷晓华. 分布式电源并网对配电系统的影响研究[J]. 电器开关, 2014, (1):51-58.

[2] 杨旭英,段建东,杨文宇,等. 含分布式发电的配电网潮流计算[J]. 电网技术, 2009, 33(18):139-143.

[3] 杨雄,卫志农,孙国强,等. 含分布式电源的配电网三相解耦潮流计算方法[J]. 电力自动化设备, 2014, 34(3):99-107.

[4] 何昌奇,邵龙,高杨,等. 分布式电源并网后对电压分布影响的研究[J]. 中国电力, 2014, 47(5): 88-91.

[5] 彭彬,刘宁,吴迪. 配电网潮流计算中的分布式电源建模[J]. 电力系统及其自动化学报, 2011, 23(2):152-156.

[6] 巨云涛,吴文传,张伯明,等. 分布式电源三相稳态模型 [J]. 中国电机工程学报, 2014, 34(10):1509-1518.

[7] FEIJOO Andres E,CIDRAS Jose. Modeling of wind farms in the load flow analysis [J]. IEEE Trans on Power Systems, 2000, 15(1):110-115.

[8] 徐青山,刘中泽,陈潇鹏,等. 含分布式电源的配电网三相时域仿真[J]. 电力自动化设备, 2015, 35(8):22-30.

[9] 顾晨,乐秀璠,张晓明. 基于改进前推回代法的弱环配电网三相潮流计算[J]. 电 力 系 统 保 护 与 控 制, 2010, 38(19):160-164.

[10] 刘耀年,岂小梅,李国鹏,等. 基于回路阻抗法的配电网潮流计算[J]. 继电器, 2004, 32(8):8-10.

[11] 索南加乐,李怀强,罗云照,等. 一种新的配网潮流常Jacobian牛顿算法[J]. 西安交通大学学报, 2002, 36(12):1222-1226.

[12] 孙健,江道灼. 基于牛顿法的配电网络Zbus潮流计算方法[J]. 电网技术, 2004, 28(15):40-44.

[13] 闫丽梅,谢明霞,徐建军,等. 含分布式电源的配电网潮流改进算法[J]. 电力系统保护与控制, 2013, 41(5):17-22.

[14] 刘波,张焰,杨娜.计及分布式电源的配电网潮流和断线故障分析算法[J].上海交通大学学报, 2008, 42(12):2028-2036.

[15] 牛焕娜,井天军,李汉成,等．基于回路分析的含分布式电源配电网简化潮流计算[J]. 电网技术,2013, 37(4):1033-1038.

[16] 彭彬,刘宁,吴迪. 配电网潮流计算中的分布式电源建模[J].电力系统及其自动化学报, 2011, 23(2):152-156.

[17] 李庚银. 电力系统分析基础[M]. 北京:机械工业出版社, 2011.

[18] BARAN M E, WU F F．Network reconfiguration in distribution systems for loss reduction and load balancing [J]．IEEE Transactions on Power Delivery, 1989, 4(2):1401-1406．

[19] 王守相,王成山. 现代配电系统分析(第二版)[M]. 北京:高等教育出版社, 2014.

Improved Power Flow Calculation Method for Distribution Network with DGs

LIANG Xiao, JIAO Yanjun, JIANG Chenyang

(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

The algorithm is improved by adjusting the Newton Method, which solves the problem of the traditional power flow calculation method for distribution network with multi-node Distributed Generation (DG). The elements in the Jacobian matrix are optimized by Steepest Descend Method and Newton Method at each iteration. The improved method solves the difficulty of the rich types of the DG nodes and the convergence difficulties of the high ratio of resistance and reactance in the Jacobian matrix. The new power flow calculation method uses the zero-impedance connection numbering program. Theoretical analysis and the IEEE33 node stimulation show that the improved algorithm can do a better job in terms of convergence and convergence rate than other traditional methods. According to the results, the new algorithm has a wider range of applications and is more suitable for fast flow analysis of power flow for distribution network with DGs and real-time scheduling computing.

Distributed Generation; power flow calculation for distribution network; Jacobian matrix; improved algorithm; zero-impedance connection numbering program

10.3969/j.ISSN.1007-2691.2016.04.10

2015-11-09.

梁宵(1991-)，女，硕士研究生，研究方向为电力系统保护及其控制；焦彦军(1963-)，男，教授，研究方向为电力系统保护及其控制；蒋晨阳(1992-)，男，硕士研究生，研究方向为电力系统分析、运行与控制及电力系统继电保护。

TM744

A

1007-2691(2016)04-0059-07