基于加权潮流冲击熵的电网节点抗干扰能力分析

徐　岩，郅　静

(华北电力大学 新能源电力系统国家重点实验室,河北 保定 071003)



基于加权潮流冲击熵的电网节点抗干扰能力分析

徐岩，郅静

(华北电力大学 新能源电力系统国家重点实验室,河北 保定 071003)

为提高电力系统运行安全水平，提出一种基于加权潮流冲击熵的电网节点抗干扰能力分析方法。当系统断线故障和负荷水平提高时，分别利用直流潮流法和功率灵敏度矩阵估算节点所连线路的潮流增量及负载率，结合该节点度数计算其加权潮流冲击熵，进而得到其受冲击指标，反映节点对系统断线故障及负荷水平提高的抗干扰能力。直流潮流法和功率灵敏度矩阵可通过简单的数学运算准确估算系统断线故障和负荷水平提高时各线路的潮流情况，计算量少，适用性好。加权潮流冲击熵反映了节点所连线路负载率偏高甚至过载时的危险性以及不同节点度数分散节点所受冲击时的差异。受冲击指标综合考虑系统断线故障和负荷水平提高对节点的冲击影响，判断节点的抗干扰能力。在IEEE39节点系统中对该方法的正确性和优越性进行了验证。

电力系统；节点抗干扰能力；加权潮流冲击熵；直流潮流法；功率灵敏度

0　引　言

电力系统中，母线故障的破坏性比线路故障更加严重[1-3]，因此需要对电网脆弱节点进行识别和重点保护。目前大部分方法在识别脆弱节点时仅强调节点在功率传输中的作用以及节点故障对电网造成的危害[4,5]，没有考虑节点对系统扰动的抗干扰能力。节点的重要性并不能完全说明节点的脆弱性，若重要节点本身抵抗干扰的能力很强，很难出现故障，其脆弱性就无法表现出来。节点的抗干扰能力决定着节点受外界扰动冲击的影响程度，与节点在电网运行中发生故障的可能性密切相关，因此，对节点的抗干扰能力进行分析具有重要意义。

节点度数指的是与该节点相连的线路数目[1]，文献[6]利用线路传输贡献度反映线路在电网各发电机——负荷节点对之间传输功率时被利用的深度和广度，并在线路传输贡献度和节点度数的基础上定义节点传输贡献度，衡量节点对电能传输的承载和贡献能力，同时指出度数大的节点在受到扰动时分散冲击的能力强，但是该方法仅利用电网正常运行时的参数去衡量节点的脆弱性，没有体现节点在系统发生扰动时受到的冲击。文献[7]通过分析节点功率增加时扰动功率在各线路的分配情况来判断各节点所能承受的最大功率波动，进而得到各负荷节点的抗干扰能力，但该方法在增加某节点功率时未指明增加出力的发电机节点，然而发电机节点的选择直接影响节点的最大功率波动值。

本文提出一种基于加权潮流冲击熵的电网节点抗干扰能力分析方法。当系统断线故障和负荷水平提高时，分别利用直流潮流法和功率灵敏度矩阵估算节点所连线路的潮流增量及负载率，结合该节点度数计算其加权潮流冲击熵，进而得到其受冲击指标，反映节点对系统断线故障及负荷水平提高的抗干扰能力。直流潮流法和功率灵敏度矩阵可通过简单的数学运算准确估算系统断线故障和负荷水平提高时各线路的潮流情况，计算量少，适用性好。加权潮流冲击熵反映了节点所连线路负载率偏高甚至过载时的危险性以及不同节点度数分散节点所受冲击时的差异，受冲击指标综合考虑系统断线故障和负荷水平提高对节点的冲击影响，判断节点的抗干扰能力。

1　节点加权潮流冲击熵

节点的抗干扰能力是指系统发生扰动时节点的受冲击程度，节点受冲击的程度越大，说明节点的抗干扰能力越差，在系统扰动时易出现故障，其脆弱性容易表现出来。节点的抗干扰能力和该节点所连线路的运行情况密切相关[1,2]，可根据扰动对节点所连线路的冲击程度及线路在扰动后的危险程度判断节点的受冲击情况和抗干扰能力。

本文综合考虑系统断线故障和负荷水平提高对节点的冲击影响，判断节点的抗干扰能力。

1.1断线故障对节点的冲击

1.1.1直流潮流法

电网中某线路断开，利用直流潮流法可快速计算其他线路的潮流转移增量，进而估算这些线路的负载率。设电网中有n个节点，采用直流潮流法[8]时，其潮流满足式(1)。

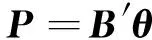
(1)

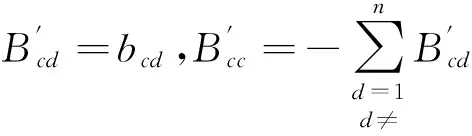
当节点注入功率不变时，某线路断开后，B′矩阵和θ列向量将偏离正常情况下的值，得到式(2)。

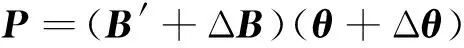
(2)

式中：ΔB和Δθ分别为B′矩阵和θ列向量的偏离量。

当lef断开时，ΔB满足式(3)。

(3)

ΔB中其它元素均为0。将式(2)展开得：

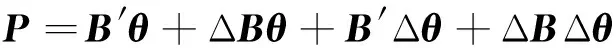
(4)

将式(1)代入式(4)可得：

(5)

当lef断开后，lcd的潮流为

(6)

因此，受潮流转移影响，线路lcd的潮流增量为

(7)

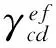
(8)

本文取线路热稳定功率极限作为其最大传输功率，实际电网运行中依情况而定。

根据以上推导，利用直流潮流法可以估算电网断线故障时其他线路的潮流增量及负载率，判断节点所连线路的受冲击情况，进而对该节点的抗干扰能力进行分析。

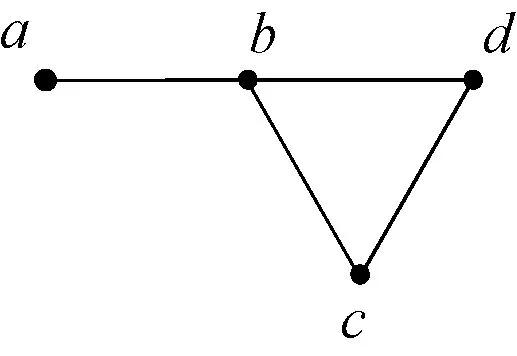
图1　通过单条线路与电网相连的节点Fig.1　Nodes connected with power grid by a single line

需要说明的是，对于仅通过单条线路与电网相连的节点，如图1中节点a，线路lbd、lbc或lcd中任一条线路断开引起的潮流转移都不会对线路lab的潮流产生影响[9,10]，lab的潮流增量近似为0，也就是说，通过单条线路与电网相连的节点受电网潮流转移的冲击很小，因此，本文不再对通过单条线路与电网相连的节点的脆弱性进行分析。同时，由于单条线路一旦断开，电网解列为两部分，各部分功率不再平衡，本文不再对这些线路进行开断分析。

1.1.2断线故障时的节点加权潮流冲击熵

文献[11,12]利用系统发生扰动时的线路潮流增量转移熵衡量线路的受冲击程度，但该方法只考虑了线路潮流增量的大小，没有考虑线路的负载率变化，然而，线路的潮流增量大不代表线路受扰动影响后的危险性大，同时，以上两种方法都没有考虑线路潮流增量为负值的情况。

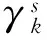
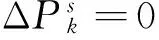
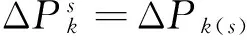
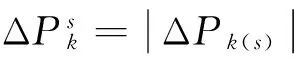
线路s断开对所有线路的潮流冲击如式(9)：

(9)

线路s断开时，线路k承担的潮流冲击占系统总潮流冲击的比例为

(10)

在线路潮流增量转移熵[11,12]的基础上，考虑线路负载率偏高甚至过载时的危险性，定义线路s断开对线路k的加权潮流冲击熵为

(11)

考虑不同节点度数在分散节点所受冲击时的差异[3,6]，线路s断开对节点i的加权潮流冲击熵为

(12)

式中：Ni为与节点i相连的线路集合；mi为节点i的度数。

式(12)中，将节点度数作为分母是考虑到节点度数不同时节点分散其所受冲击的能力不同。若某些危险性高的线路导致其所连节点受到的冲击很大，当节点度数较大时，其受到的扰动能量可以沿与之相连的多条安全线路分摊传递，而当节点度数较小时，其受到的扰动能量相对集中，易引发节点故障[3,6]。

分别以系统中线路为开断线路，可得节点i的加权潮流冲击熵Ri如式(13)所示。

(13)

式中：w为单条线路断开即造成解列的线路数目。

Ri越大，说明节点i受系统断线故障的影响越大，对线路断开扰动的抵抗能力越差。

对节点加权潮流冲击熵分析如下：

(1)本文考虑了线路增量为负值时线路潮流的受冲击情况，在线路潮流增量转移熵[11,12]的基础上，考虑线路负载率偏高甚至过载时的危险性和不同节点度数在分散节点所受冲击时的差异，定义加权潮流冲击熵反映节点的受冲击程度；

(2)计算节点加权潮流冲击熵时，将线路负载率作为权值，对于过载线路取负载率扩大倍数α>1，突出了线路负载率偏高甚至过载时的危险性，克服了以往方法仅以潮流增量判断线路受冲击程度的缺点。

1.2负荷水平提高对节点的冲击

1.2.1功率灵敏度

当不计电力电子等非线性元件时，将发电机、负荷都作为节点注入电流表示，电网中支路电流和节点注入电流之间为线性关系[13]，如式(14)所示。

(14)

式中：IB为支路电流列向量；IN为节点注入电流列向量；YB为支路电纳矩阵；A为节点关联矩阵；YN为节点电纳矩阵。

(15)

为得到线路功率与节点注入功率之间的关系，对式(15)进行处理得到式(16)：

(16)

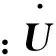
(17)

式中：Pk,B和Qk,B分别为支路k的有功功率和无功功率，Uk,B和φk,B分别为支路k首端电压模值和相角，Ui,N和φi,N分别为第i个节点电压模值和相角。

将式(17)展开，得到实数部分如下：

为得到节点注入功率变化时线路功率的变化情况，将式(18)中支路有功功率和节点注入有功功率取变量形式，并将节点注入无功功率变量取0，可得式(19)。

(19)

定义矩阵D(β)为支路功率变量与节点注入功率变量之间的功率灵敏度矩阵，其中支路k功率变量与节点i注入功率变量之间的功率灵敏度βk-i为

(20)

因此，当系统负荷及发电水平变化时，可得线路k的功率增量为

(21)

功率灵敏度矩阵结合网络拓扑参数和实际电网运行情况衡量节点注入功率对线路功率的影响。

利用式(21)可以估算电网负荷水平及发电水平提高时各线路的潮流增量及负载率，判断节点所连线路的受冲击情况，进而对该节点的抗干扰能力进行分析。

1.2.2负荷水平提高时的节点加权潮流冲击熵

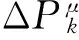
(22)

线路k的加权潮流冲击熵为

(23)

其中，α为负载率扩大倍数，其取值与1.1.2节相同。

由图8可以看出两者存在较强的相关性(经计算得其相关系数为0.529)。在无法求得重建误差的情况下,可以用距离误差估计重建结果的好坏。

节点i的加权潮流冲击熵为

(24)

式中：Ni为与节点i相连的线路集合；mi为节点i的度数。

2　节点受冲击指标

分别对系统断线故障和负荷水平提高时的节点加权潮流冲击熵进行归一化处理[3,14]，归一化公式如式(25)所示。

(25)

综合考虑节点受到系统断线故障和负荷水平提高时的冲击，定义节点i的受冲击指标φi如式(26)所示。

(26)

节点受冲击指标综合考虑节点受到系统断线故障和负荷水平提高时的冲击来分析节点的抗干扰能力，节点受冲击指标越大，其抗干扰能力越差。

3　仿真算例

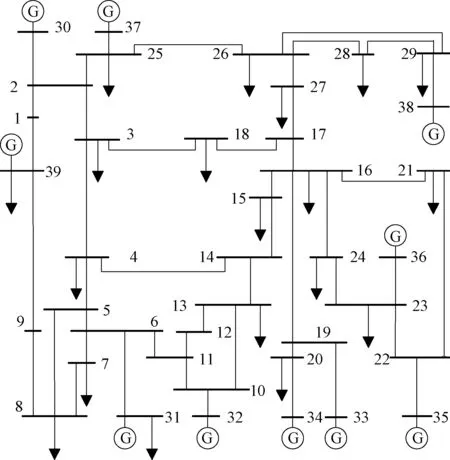
图2　IEEE39节点系统Fig.2　IEEE39 bus system

3.1对直流潮流法估算准确性的验证

为验证直流潮流法估算断线故障时其他线路潮流增量的准确性，以断开线路14-4为例，将利用直流潮流法估算的各线路潮流增量与利用PSASP仿真软件得到的各线路潮流增量列于表1，其中，ΔP1是利用直流潮流法所得的线路潮流增量，ΔP2是利用PSASP仿真软件所得的线路潮流增量。

观察表1可得，利用直流潮流法可准确估算系统断线故障时其他线路的潮流增量，进而计算节点加权潮流冲击熵，判断节点的受冲击程度及抗干扰能力，同时，直流潮流法计算简单，运算量少，适用性好。

3.2对功率灵敏度矩阵估算准确性的验证

为验证功率灵敏度矩阵估算负荷及发电水平提高时各线路的潮流增量的准确性，以负荷及发电水平增加比例为μ=0.1为例，将利用功率灵敏度矩阵估算的各线路潮流增量与利用PSASP仿真软件得到的各线路潮流增量列于表2，其中，ΔP1是利用功率灵敏度矩阵所得的线路潮流增量，ΔP2是利用PSASP仿真软件所得的线路潮流增量。

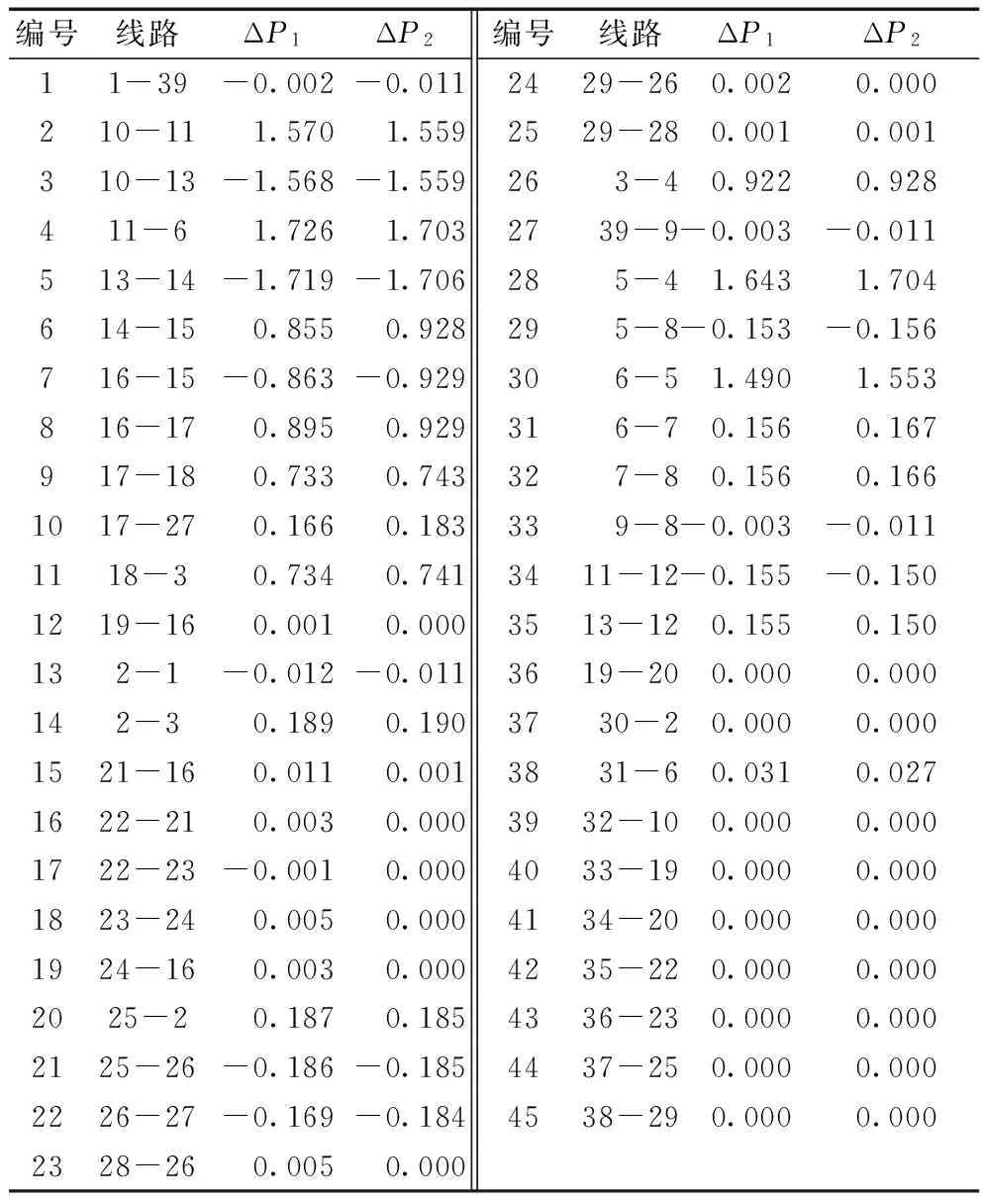
表1　直流潮流法估算结果准确度验证

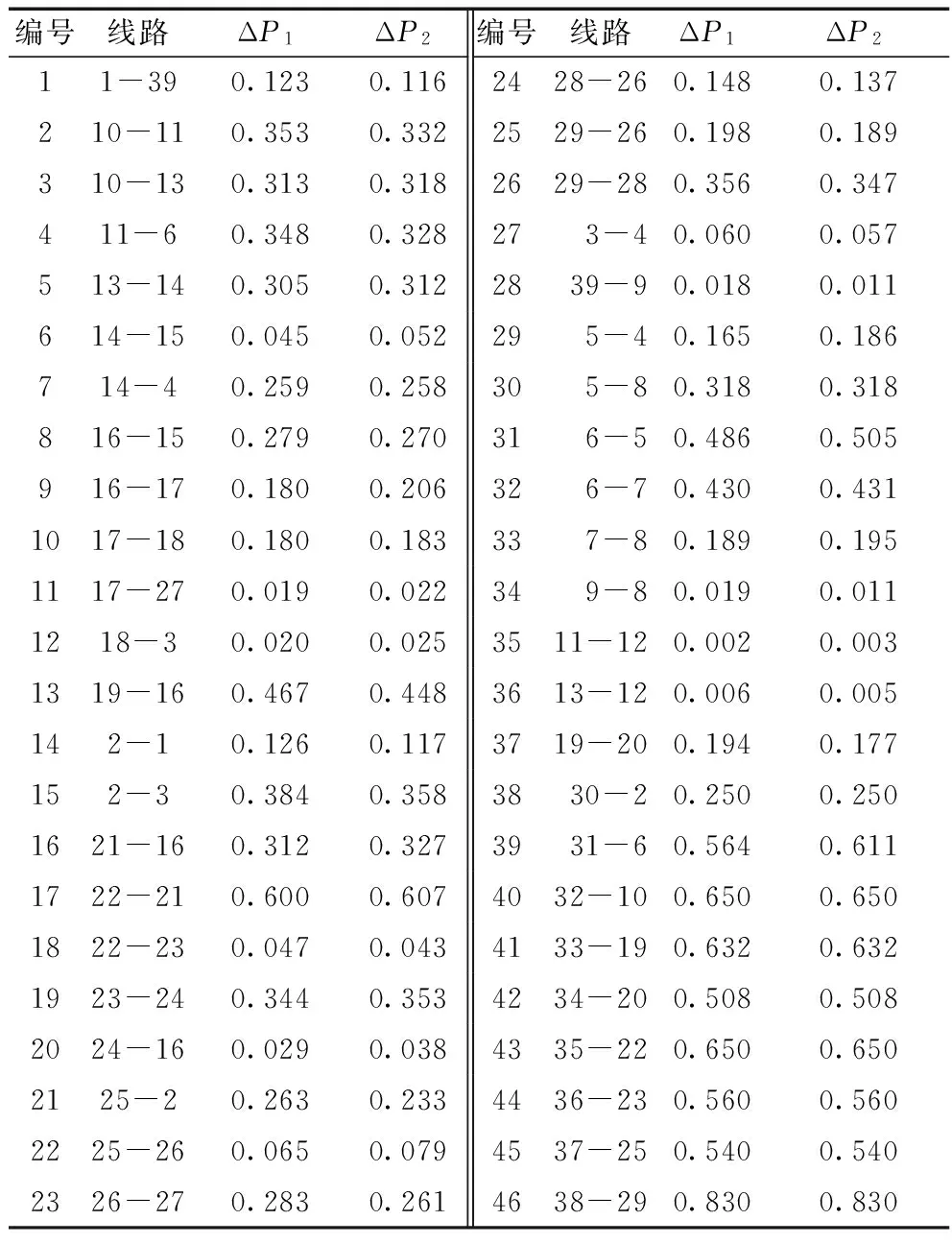
表2　功率灵敏度矩阵估算结果准确度验证

观察表2，利用功率灵敏度矩阵，通过简单的数学运算即可准确估算系统负荷及发电水平提高时各线路的潮流增量，进而计算节点加权潮流冲击熵。基于功率灵敏度矩阵，根据电网运行数据可方便得到系统负荷水平提高时各节点的抗干扰能力，避免了繁冗的仿真运算，减少了运算量。

3.3节点抗干扰能力分析

利用本文方法计算各节点的受冲击指标，并按照从大到小的顺序对节点进行排序，排序前13位的节点如表3所示。

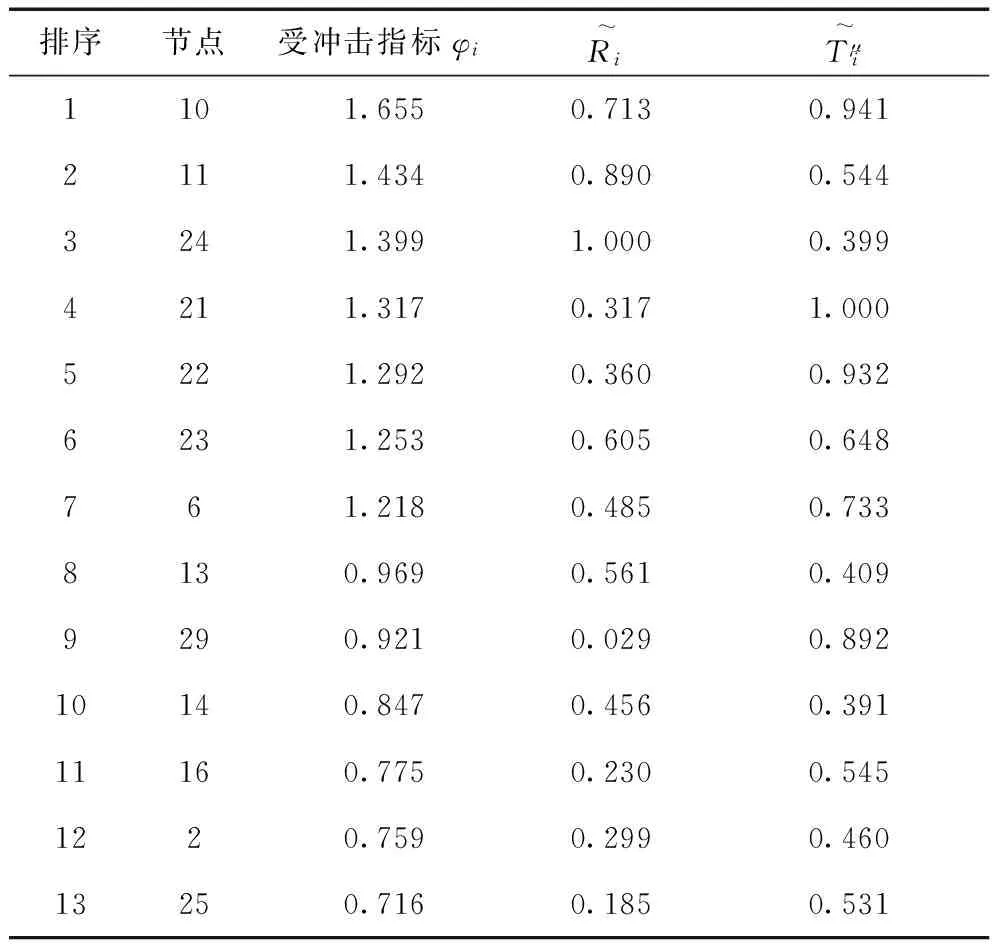
表3　本文方法识别的抗干扰能力较差的节点

将本文方法与文献[2,3]识别的抗干扰能力较差的节点进行对比，如表4所示，为便于比较，除去其他方法识别的通过单条线路与电网相连的节点。

表4　各方法识别的抗干扰能力较差的节点

若利用文献[11,12]中的潮流增量转移熵衡量节点的受冲击程度，即计算节点加权潮流冲击熵时不再以负载率为权值，同时去掉负载率扩大倍数，其余部分与本文保持相同，得到的各节点受冲击指标如表5所示。

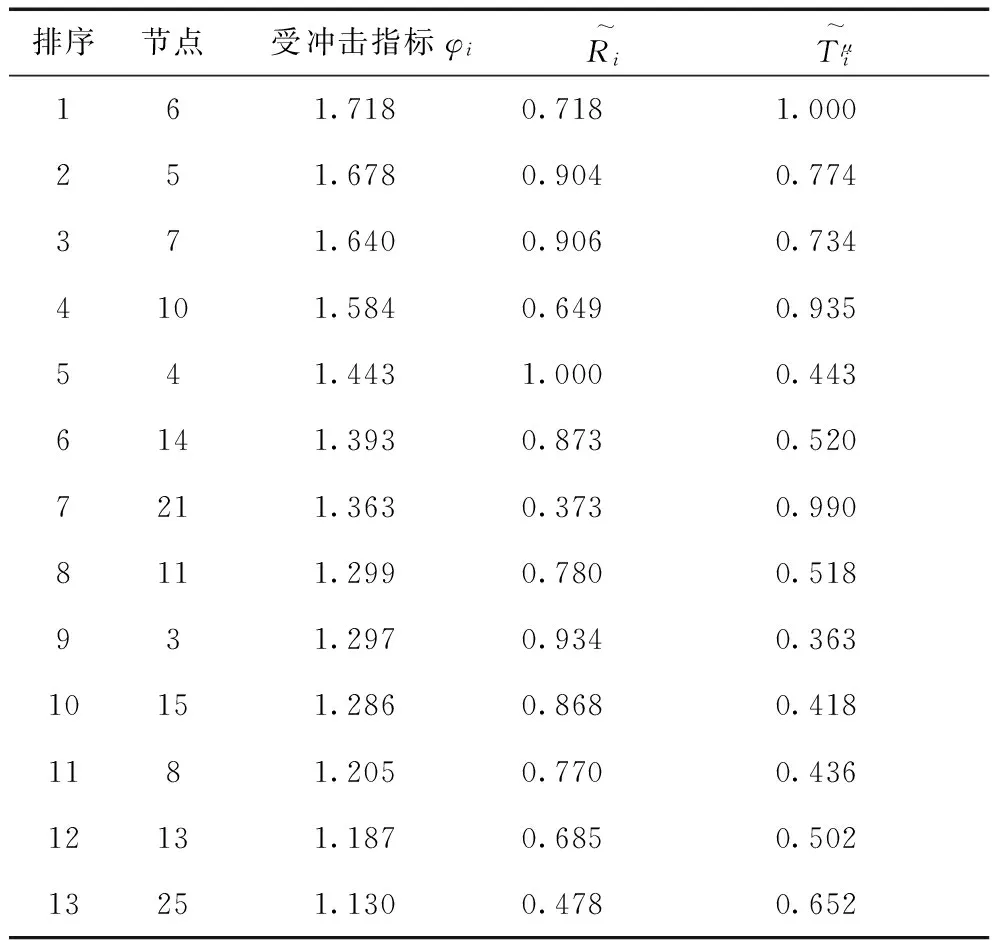
表5　基于潮流增量转移熵识别的抗干扰能力较差的节点

仿真分析：

(1)表3中识别的抗干扰能力较差的节点中，部分节点与发电机节点相连，在系统负荷水平提高时会受到较大冲击，如节点10、22、23、6、29、2、25；部分节点所连线路均为重载线路，发生线路断开或电网负荷水平增加时很容易发生过载，如节点10、11、24、21、22、23、6、13、14、2、25；部分节点处于电网的枢纽位置，所连线路均为电网的关键输电通道，如节点16担负着将发电机33、34、35、36的功率送出的重要任务，且线路16-15和16-17一旦同时断开，系统即发生解列，同时，这两条线路受对方断开的转移潮流影响很大，易发生过载。

(2)观察表3和表4，虽然从不同角度出发判断的节点抗干扰能力排序有差异，但文献[2,3]识别的易受冲击影响的节点全部都位于本文方法所识别的节点集中，验证了本文方法的正确性。

同时，本文方法识别了文献[2,3]未识别出的节点24、13和14，这些节点所连线路的负载率很高，在电网发生扰动时很容易发生过载，节点受到的冲击大，抗干扰能力差，需要重点监测和保护。

(3)对比表3、表4和表5，当仅考虑扰动对线路潮流增量的影响时，利用潮流增量转移熵识别的抗干扰能力较差的节点中，会忽略节点24、22、23、29、16、2，通过上文分析及文献[2,3]识别结果，可知这些节点受扰动的冲击影响较大，属于易故障节点。

因此，加权潮流冲击熵有效反映了所连线路负载率偏高甚至过载时的节点脆弱性，使识别结果更加准确，同时，考虑了不同节点度数在分散节点所受冲击时的差异，更加符合电网实际。

受冲击指标综合考虑节点在系统断线故障和负荷水平提高时受冲击的影响程度。

(5)计算加权潮流冲击熵时，为突出线路过载的危险性，本文取过载线路的负载率扩大倍数α=10，相当于是把过载线路的负载率扩大了10倍，对于α的取值没有特定要求，只要能够突出线路过载危险性的合适取值均可。

4　结　论

提出一种基于加权潮流冲击熵的电网节点抗干扰能力分析方法。该方法的主要优点有：

(1)当系统断线故障和负荷水平提高时，分别利用直流潮流法和功率灵敏度矩阵估算节点所连线路的潮流增量及负载率，减少了计算量，提高了实际适用性。

(2)利用节点所连线路的潮流增量、过载率及节点度数计算节点加权潮流冲击熵。加权潮流冲击熵反映了节点所连线路负载率偏高甚至过载时的危险性以及不同节点度数分散节点所受冲击时的差异。

(3)受冲击指标综合考虑系统断线故障和负荷水平提高对节点的冲击影响，判断节点的抗干扰能力。

本文方法虽有一定的有效性，但仅从节点相连线路所受的潮流冲击的角度判断节点的受冲击程度，没有考虑节点的电压等因素，如何更全面的衡量节点的抗干扰能力是下一步的研究方向。

[1] 陈晓刚，孙可，曹一家．基于复杂网络理论的大电网结构脆弱性分析[J]．电工技术学报，2007，22(10)：138-144．

[2] 雷成，刘俊勇，刘友波，等．考虑元件关联性的节点综合脆弱评估模型[J]．华东电力，2013，41(8)：1663-1667．

[3] 雷成，刘俊勇，魏震波，等．计及网络传导能力与抗干扰能力的节点综合脆弱评估模型[J]．电力自动化设备，2014，34(7)：144-149．

[4] 王涛，高成彬，顾雪平，等．基于功率介数的电网关键环节辨识[J]．电网技术，2014，38(7)：1907-1913．

[5] 徐林，王秀丽，王锡凡．基于电气介数的电网连锁故障传播机制与积极防御[J]．中国电机工程学报，2010，30(13)：61-68．

[6] 鞠文云，李银红．基于最大流传输贡献度的电力网关键线路和节点辨识[J]．电力系统自动化，2012，36(9)：6-12．

[7] 靳冰洁，张步涵，姚建国，等．基于信息熵的大型电力系统元件脆弱性评估[J]．电力系统自动化，2015，39(5)：61-68．

[8] 吴际舜．电力系统静态安全分析[M]．上海：上海交通大学出版社，1985．

[9] 杨文辉，毕天姝，薛安成，等．基于图论的潮流转移路径的快速搜索[J]．电网技术，2012，36(4)：84-88．

[10] 徐岩，郅静．基于广域测量系统的潮流转移关键线路快速搜索 [J]．华北电力大学学报，2014，41(5)：49-54．

[11] 李勇，刘俊勇，刘晓宇，等．基于潮流熵的电网连锁故障传播元件的脆弱性评估[J]．电力系统自动化，2012，36(19)：11-16．

[12] 李勇，刘俊勇，刘晓宇，等．基于潮流熵测度的连锁故障脆弱线路评估及其在四川主干电网中的应用[J]．电力自动化设备，2013，33(10)：40-46．

[13] 徐慧明，毕天妹，黄少锋，等．基于广域同步测量系统的预防连锁跳闸控制策略[J]．中国电机工程学报，2007，27(19)：32-38．

[14] 董卓，朱永利，胡资斌．基于遗传规划和数据归一化的变压器故障诊断[J]．电力科学与工程，2011，27(9)：31-34，54．

Analysis of Node Anti-jamming Capability Based on the Weighted Power Shock Entropy in Power System

XU Yan, ZHI Jing

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Baoding 071003, China)

To improve the operation safety level of power system, an analysis method of node anti-jamming capability based on the weighted power shock entropy in power system is put forward. When line disconnection and improved load level happens, the direct current power flow method and power sensitivity matrix are respectively used to estimate the power increment and load rate of lines connected with the node. Combined with the node degree, the weighted power shock entropy and the impact index are calculated to reflect the impact of line disconnection and improved load level. The direct current power flow method and power sensitivity matrix can accurately estimate the line power with line disconnection and improved load level by simple mathematical operations. The calculation amount is little and the applicability is good. The weighted power shock entropy can reflect the risk of the high load rate even overload, as well as the different shock dispersion capacity by different node degree. The impact index of node is defined to reflect the node anti-jamming capability. The method considers the shock impact on the node caused by line disconnection disturbance and improved load level comprehensively. The correctness and superiority of the proposed method are verified in IEEE39 bus system.

power system; the node anti-jamming capability; the weighted power shock entropy; the direct current power flow method; power sensitivity matrix

10.3969/j.ISSN.1007-2691.2016.04.06

2015-08-29.

国家自然科学基金资助项目(50777016)；中央高校基本科研业务费专项资金项目(12MS110).

徐岩(1976-)，男，副教授，研究方向为电力系统保护与安全控制，新能源发电和智能电网；郅静(1990-)，女，硕士研究生，研究方向为电力系统保护与安全控制。

TM711

A

1007-2691(2016)04-0034-08