极大3等周边连通图的充分条件

徐子钧,张磊

(晋中学院数学学院, 山西 晋中 030600)



极大3等周边连通图的充分条件

徐子钧,张磊*

(晋中学院数学学院, 山西 晋中 030600)

摘要：k等周边连通度是一个比边连通度更可靠的网络可靠性参数。 连通图G的k等周边连通度定义为:X⊆≥k},其中=V(G)X。令:X⊆=k}。图G是极大k等周边连通的如果γk(G)=βk(G)。令G是一个阶至少为6的连通图。本文证明了如果对于G中任意一对不相邻的顶点u,v,当u和v都不在三角形中时满足≥2;当u和v中至少有一个在三角形中时满足≥5,那么G是极大3等周边连通的。

关键词：互连网络;极大k等周边连通图;k等周边连通度;邻域

1　引言

定义1.1设k是一个正整数,G是一个阶至少为2k的连通图。G的k等周边连通度定义为:

令

显然,γk(G)≤βk(G)。 2007年,Zhang等[8]给出了极大k等周边连通图的定义。

定义1.2设k是一个正整数, G是一个阶υ≥2k的连通图。如果γk(G)=βk(G), 那么称G是极大k等周边连通的。

2009年,Wang等[9]给出了一个极大k等周边图的邻域条件。

定理1.4[9]设k是一个正整数, G是一个阶至少为2k的图。如果对G中任意两个不相邻顶点u,v都有

那么G是极大k等周边连通图。

本文将给出极大3等周边连通图的邻域条件, 这个结果在k=3时, 改进了定理1.4。

2　主要结论

(1)如果在X中存在一个基数为k的子集U使得

那么G是极大k等周边连通的。

(2)X中不存在基数为k的子集U使得

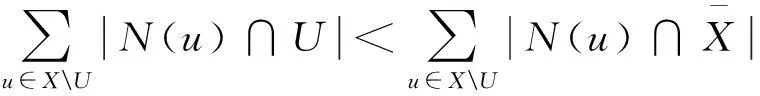
定理2.2设G是一个阶至少为6的连通图。如果对于G中任意不相邻的顶点u和v,当u,v都不在三角形中时，满足

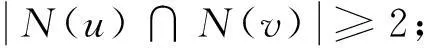
当u,v至少有一个在三角形中时，满足

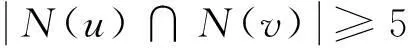
那么G是极大3等周边连通的。

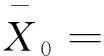
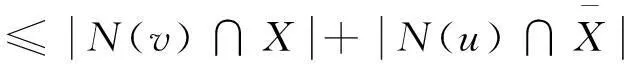
=0。

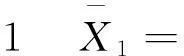
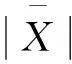
由引理2.1(1)知,G是极大3等周边连通的。

由引理2.1(1)知,G是极大3等周边连通的。

≥3,

则

由引理2.1(1)知,G是极大3等周边连通的。

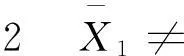
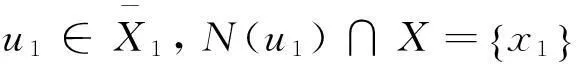
=1,

与假设矛盾。因此,X0=∅。设H2为G[X]中包含{x1}∪X1中尽可能多的点且包含边的数目最多的3阶子图。

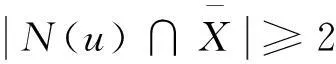
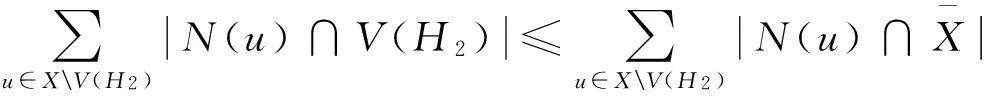
由引理2.1(1)知,G是极大3等周边连通的。

=3,

矛盾。

易知X1{x1}≠∅。注意到N(u1)∩X={x1}。则对于任意的v∈X{x1},v与u1都不相邻。根据题意,我们有

=2。

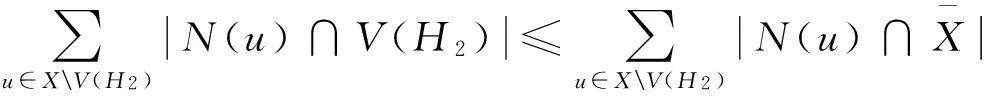
由引理2.1(1)知,G是极大3等周边连通的。

=3,

矛盾。

由定理2.2,我们容易得到下面的结论。

推论2.3设G是一个阶至少为6的无三角形连通图。如果对于G中任意一对不相邻的顶点u,v都有

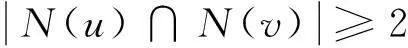
那么G是极大3等周边连通的。

参考文献：

[1]BONDY J A,MURTY U S R. Graph Theory[M].New York:Springer,2008.

[3]WANG MING,LI QIAO.Conditional edge connectivity properties, reliability comparisons and transitivity of graphs[J]. Discrete Mathematics, 2002, 258(1/2/3): 205-214.

[4]LI Q,LI Q.Reliability analysis of circulant graphs[J]. Networks, 1998,31(2): 61-65.

[5]XU J M,XU K L.On restricted edge-connectivity of graphs[J]. Discrete Mathematics, 2002, 243(1/2/3): 291-298.

[6]BOESCH F T. On unreliability polynomials and graph connectivity in reliable network synthesis[J]. Journal of Graph Theory, 1986, 10(3): 339-352.

[8]ZHANG Z,YUAN J J.Degree conditions for restricted-edge-connectivity and isoperimetric-edge-connectivity to be optimal[J]. Discrete Mathematics, 2007, 307(2): 293-298.

[9]WANG S Y,LIN S W,LI C F.Sufficient conditions for super k-restricted edge connectivity in graphs of diameter 2[J]. Discrete Mathematics, 2009, 309(9): 908-919.

DOI:10.3976/j.issn.1002-4026.2016.04.015

收稿日期：2015-10-19

作者简介：徐子钧(1987-)，女，硕士，助教，研究方向为图论及其应用。Emali: huayuycdi@yeah.net

*通信作者。

中图分类号：O157.6

文献标识码：A

文章编号：1002-4026(2016)04-0075-05

Sufficient conditions of a maximally 3-isoperimetric edge connected graph

XU Zi-jun,ZHANG Lei*

(School of Mathematics, Jinzhong University, Jinzhong 030600, China)

Abstract∶k-isoperimetric edge connectivity is a more reliable network reliability index than edge connectivity. k-isoperimetric edge connectivity of a connected graph G is defined as :X⊆≥k},where =V(G)X. Let :X⊆=k}. A graph G is maximally k-isoperimetric edge connected if γk(G)=βk(G). Let G be a connected graph of at least order 6. We prove that for any pair of nonadjacent vertices u,v in G, ≥2 holds when u and v are not on a triangle. If ≥5 holds for u or v on a triangle, then G is maximally 3-isoperimetric edge connected.Key words∶interconnection networks; maximally k-isoperimetric edge connected graph; k-isoperimetric edge connectivity; neighborhood