基于纵倾与侧斜的螺旋桨优化设计

任万龙，郝宗睿，周忠海，徐娟，王越

(1. 山东省科学院海洋仪器仪表研究所，山东 青岛 266001；2.山东省海洋仪器仪表科技中心，山东 青岛 266001)



基于纵倾与侧斜的螺旋桨优化设计

任万龙1，2，郝宗睿1*，周忠海1，徐娟1，王越1

(1. 山东省科学院海洋仪器仪表研究所，山东 青岛 266001；2.山东省海洋仪器仪表科技中心，山东 青岛 266001)

摘要：螺旋桨的特征参数之间相互制约、影响，共同决定着螺旋桨的水动力、空泡以及振动等性能。本文以粒子群算法为工具，基于面元法理论，以4382型螺旋桨为模型桨，以侧斜、纵倾为优化变量对其进行优化设计。侧斜和纵倾采用贝塞尔曲线拟合方式进行综合考虑，以螺旋桨的效率为优化目标，对原桨及优化桨进行水动力性能分析。优化后桨叶的效率提高，压力分布得到改善，很好的抑制了空泡的发生。

关键词：纵倾;侧斜;粒子群算法;面元法;螺旋桨

现代的船舶行业发展迅速，随着人们环保、节能意识的提高，学者们开始研究如何在船舶高效运行的同时实现节能环保。螺旋桨作为船舶的主要推进装置，其优化设计方法受到船舶工程界的日益关注。周剑等[1]研究了基于侧斜的大侧斜螺旋桨的优化设计方法。周斌等[2-3]基于桨叶剖面，分别采用粒子群算法和遗传算法进行桨叶剖面的优化设计，从而提高了桨的效率。赵威等[4-6]利用优化软件ISIGHT，基于螺距和拱度分布对螺旋桨进行了优化设计，采用的是升力面预报方法。升力面预报桨的水动力性能与面元法预报的结果有一定的差距，目前普遍采用面元法。

螺旋桨本身有很多可控参数如螺距、侧斜及纵倾等，有诸多学者已经研究了基于螺距等桨叶参数的优化，取得了一定的成果。但是，基于侧斜、纵倾等螺旋桨参数的优化鲜有学者涉及。因此，本文着重探讨基于侧斜及纵倾的螺旋桨优化设计。

本文基于螺旋桨水动力性能的面元理论预报程序，利用智能优化理论中的粒子群优化算法进行桨叶纵倾和侧斜的优化设计研究。以DTRC4382螺旋桨为母型桨，选取侧斜、纵倾等为优化变量，进行优化设计(桨叶其他参数与母型桨相同)，得到优化后的新桨，并分别对优化结果进行分析。

1　基本理论

1.1粒子群算法

粒子群算法(PSO)是一种进化计算技术，1995年由Eberhart等提出[7]，其数学描述为：设搜索空间为D维，总粒子数为n，第i个粒子位置表示为向量xi=(xi1,xi2,…,xiD)，代表n维空间中的一个点。第i个粒子的位置变化率(速度)为向量vi=(vi1,vi2,…,viD)。根据目标函数计算得到的适应值比较粒子位置的好坏，记第i个粒子迄今为止搜索到的最优位置为pbesti=(Pi1,Pi2,…,PiD)，整个群体迄今为止搜索到的最优位置为gbest=(g1,g2,…,gN)。进化过程中各个粒子带有惯性权重ω的进化公式如下[8]:

(1)

式中,w为惯性权值，反映了算法在全局搜索和局部搜索之间的选择；c1、c2为非负常数，称为认知和社会参数；r1、r2为[0,1]之间的随机数；k为压缩因子对粒子的飞行速度进行约束。通常还需要对粒子中每维的位置和速度变化设置一个范围，如超过这个范围则将其设置为边界值，粒子群的初始位置和速度由随机产生[9]。

1.2侧斜和纵倾分布的表达方法

对于螺旋桨侧斜和纵倾沿径向分布，均可采用贝塞尔曲线法表达。由于贝赛尔曲线有着优良的性质，可以通过简单的几个控制点来控制整条曲线，绘出的曲线平滑光顺，既方便简洁又能满足要求，目前广泛应用于工程实践中，是大家经常采用的曲线拟合方式之一[10]。贝赛尔曲线广泛应用于计算机绘图、机械设计制造、航空航天以及船舶设计领域中型线和曲面的绘制。

首先，确定空间基点的坐标Pi(i=0,1,2,…,n)，可通过下式确定曲线上各点的坐标：

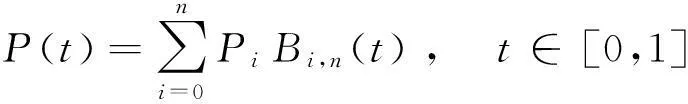
(2)

式中，Pi为构成贝塞尔曲线的特征多边形的第i个顶点，Bi,n(t)为伯恩斯坦基函数[11]：

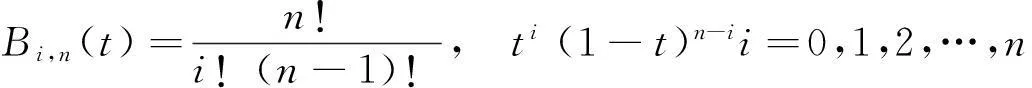
(3)

螺旋桨的侧斜、纵倾在不同的径向处有不同的值，进行优化时，需要重新获得不同径向处的侧斜、纵倾值，其表现为一条曲线。将不同径向处的侧斜、纵倾看成一条待拟合的贝塞尔曲线，然后对这条曲线进行控制，从而获得不同径向处的新的侧斜、纵倾值。

2　模型参数及目标函数

螺旋桨优化设计中，侧斜和纵倾是组成螺旋桨几何外形的重要参数，因此，本文以DTRC4382型螺旋桨为原型，基于粒子群算法，结合面元法预报螺旋桨水动力性能程序[12-13]，以保证原桨的推力要求为条件，同时以改善螺旋桨敞水效率为目标，对桨叶侧斜、纵倾径向分布曲线进行优化。表1中给出了4382系列桨模的编号和主要几何参数[14]。

表1　DTRC4382桨的主要参数

螺旋桨进行优化时，首先要满足推力要求,只有在满足推力的情况下才能追求其他条件。本文限制推力系数变化不得低于原推力系数，即为满足推力要求。将螺旋桨的敞水效率作为优化目标，从而对桨进行优化。

3　基于侧斜及纵倾的螺旋桨优化

3.1优化算例分析

图1为4382桨在优化过程中优化目标(敞水效率)随着迭代次数的增加而变化，最终收敛。从图中可以看出迭代到第10步时，优化终止，从y轴可以看出优化效率变化。优化后得到的侧斜分布与原桨的侧斜分布对比见图2，侧斜在叶梢部分变化较大，叶跟部分变化较小；优化后纵倾分布与原桨的纵倾分布对比见图3，图中叶梢部分变化较大，叶根部分变化较小。图中R为螺旋桨的半径，r为不同剖面处的半径，r/R为无因次径向位置。

从图2～3中可以看出，选取侧斜和纵倾为优化变量，优化后的螺旋桨具有较高的螺旋桨效率。随着优化的进行，效率的提高会逐渐减小。

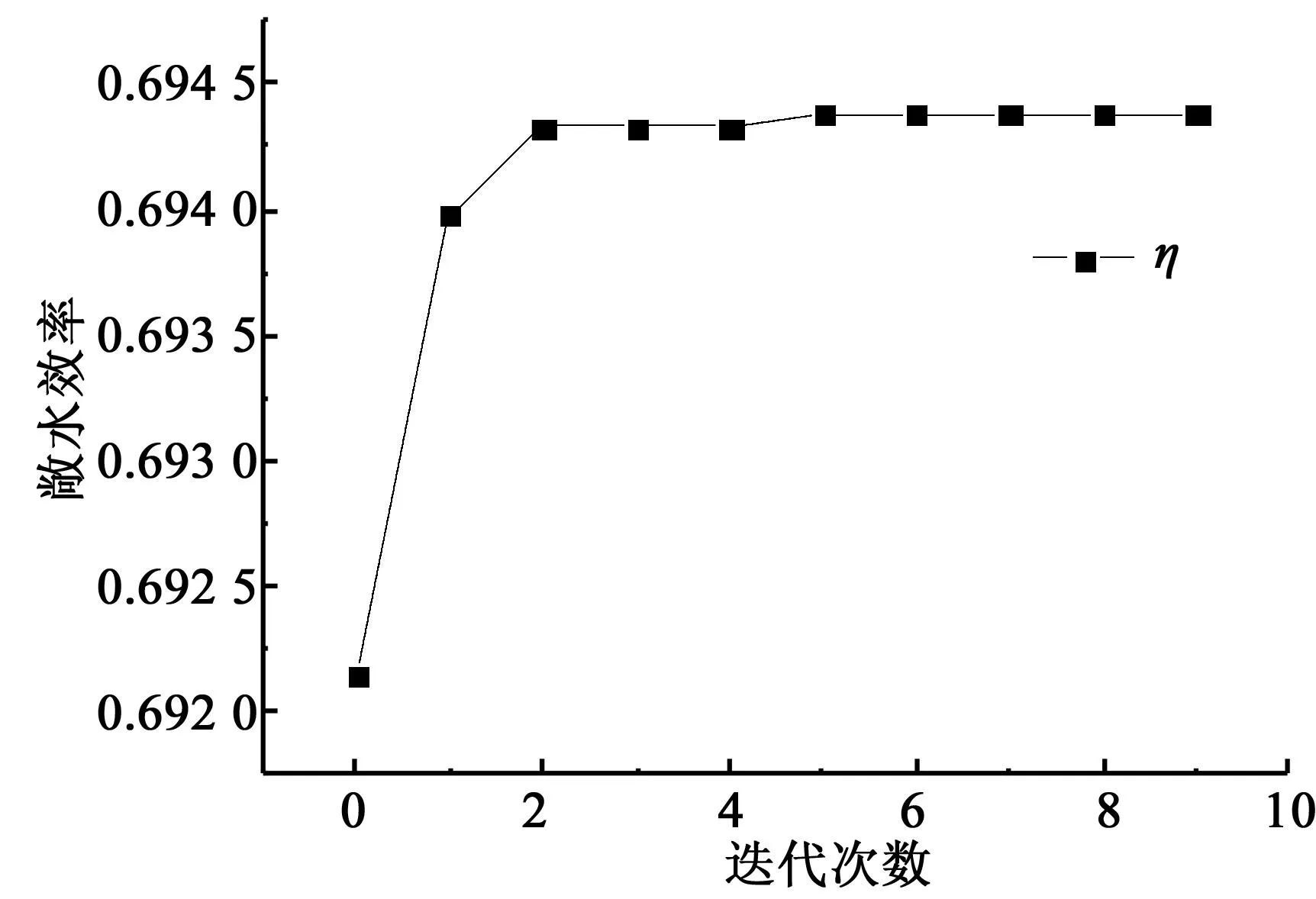
图1　优化过程示意图Fig.1　Illustration of optimization process

图2　优化纵倾变化Fig.2　 Variation of optimized rake

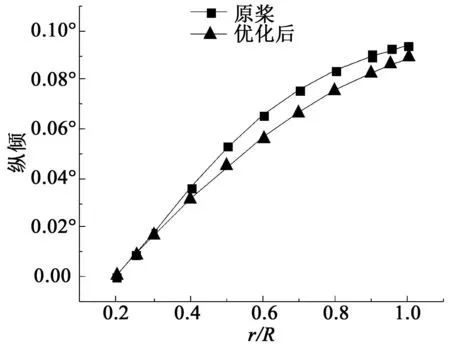
图3　优化侧斜变化Fig.3　Variation of optimized skew

图4显示了优化前后螺旋桨0.3R、0.7R、0.9R、0.95R处的压力分布。从中可以看出叶背压力变化较大，叶面变化较小。其中纵坐标为压力系数，横坐标为无因次弦向位置，x为不同的弦向位置，c为不同剖面处的弦长。

图4　优化前后压力分布的变化Fig.4　Variation of pressure distribution before and after optimization

3.2不同进速下新桨性能分析

为了更加准确地体现新桨的性能，本文给出多个进速下新桨的性能参数，进行对比分析。表2给出了4382螺旋桨优化前后推力系数Kt、扭矩系数Kq、敞水效率η的对比，从中可以发现，优化后螺旋桨的效率均有所提升，同时保证了螺旋桨的推力。在整个进速范围内，螺旋桨的效率均有提高，在设计进速处效率提高明显，同时也满足了螺旋桨推力的要求。因此，将侧斜与纵倾综合考虑，进行螺旋桨优化设计是可行的。

表2　优化前后对比

4　结语

本文以4382型螺旋桨为母型桨，以侧斜和纵倾为优化变量，基于势流面元法理论，结合粒子群算法，开展了一系列的计算和分析，得出以下结论：

(1)在设计进速下，以侧斜和纵倾为优化变量，得到优化后的桨，侧斜与纵倾发生变化，螺旋桨效率得到提高，桨叶剖面叶根处的压力分布变化较大，叶梢处几乎无变化。

(2)在常用进速系数范围内，优化桨敞水效率、推力系数均得到改善，证明本文提出的方法进行螺旋桨优化设计是可行的。

可以看出，以侧斜和纵倾为优化变量的螺旋桨优化设计，压力分布变化较小，效率得到一定的提高。该研究验证了以侧斜和纵倾为优化变量进行螺旋桨优化设计的可行性，为后续进行螺旋桨多参数多目标优化设计奠定了基础。本文采用贝塞尔曲线进行纵倾与侧斜拟合，由于贝塞尔曲线控制点较少，不能全面反映纵倾、侧斜变化，对优化结果会产生一定的影响，后续可对纵倾、侧斜的拟合方式进行进一步的研究。

参考文献：

[1]周剑.大侧斜螺旋桨的设计方法研究[D].哈尔滨:哈尔滨工程大学,2010.

[2]周斌.四桨两舵大型船舶螺旋桨的面元法设计研究[D].哈尔滨:哈尔滨工程大学,2010:68-69.

[3]黄树权.基于遗传算法的螺旋桨性能优化研究[D].大连:大连理工大学,2009:55-56.

[4]赵威,杨晨俊.船舶螺旋桨螺距及拱度的优化设计研究[J].中国造船,2010,51(1):1-8.

[5]程成, 须文波, 冷文浩. 基于 ISIGHT平台 DOE 方法的螺旋桨敞水性能优化设计[J]. 计算机工程与设计, 2007,28 (6): 1455-1459.

[6]赵威.船用螺旋桨优化设计及参数研究[D].上海:上海交通大学,2008.

[7]LEE C S，KIM Y G，SUH J C.A surface panel method for design of hydrofoils[J].Journal of Ship Research, 1994,38(3):175-181.[8]EPPLER R, SOMERS D M. A computer program for the design and analysis of low speed airfoils [Z]. NASA-TM-80210,1980.

[9]王宏亮,席光. 多目标优化设计方法在翼型气动优化设计中的应用[J].工程热物理学报.2008.29(7):1129-1132.

[10]PIEGL L, TILLER W.非均匀有理B样条 [M].北京：清华大学出版社,2010.

[11]付鹏飞.贝塞尔曲线在汽车设计中的应用[J].企业技术开发. 2012,31(26):46-47.

[12]刘洋浩. 两种不同优化算法在螺旋桨设计中的应用和比较[D].哈尔滨:哈尔滨工程大学,2012.

[13]苏玉民,黄胜.船舶螺旋桨理论[M].哈尔滨:哈尔滨工程大学出版社.2003.

[14]谭廷寿.非均匀流场中螺旋桨性能预报和理论设计研究[D].武汉:武汉理工大学.2003:25-26.

DOI:10.3976/j.issn.1002-4026.2016.04.002

收稿日期：2016-04-25

基金项目：国家自然科学基金(51206101)

作者简介：任万龙(1987-)，男，研究实习员，研究方向为流体机械设计及优化。 *通信作者，郝宗睿(1983-)，男，副研究员，研究方向为流体机械设计及优化。Email:haozr@sina.com.

中图分类号：U664.33

文献标识码：A

文章编号：1002-4026(2016)04-0007-05

Rake and skew based optimization design of a propeller

REN Wan-long1,2, HAO Zong-rui1*, ZHOU Zhong-hai1,XU Juan1, WANG Yue1

(1. Institute of Oceanographic Instrumentation, Shandong Academy of Sciences, Qingdao 266001, China;2. Shandong Scientific and Technological Center of Oceanographic Instrumentation, Qingdao 266001, China)

Abstract∶Characteristic parameters of a propeller restrict and interact with each other. They jointly determine hydrodynamics, cavitation, and vibration of a propeller. We perform its optimization design with particle swarm optimization (PSO) algorithm as a tool, panel method, DTRC 4382 propeller as a model and skew and rake as optimization variables. Skew and rake are settled with Bessel curve fitting. We further analyze hydrodynamic property of original and optimized propellers with the efficiency of a propeller as an optimization objective.We increase the efficiency of a propeller, improve its pressure distribution, and well inhibit its cavitation.

Key words∶rake; skew;PSO;panel method;propeller

【海洋科技与装备】