Triangle软件在自适应剖分中的应用

张衍林，梅　钢，徐能雄

(中国地质大学(北京) 工程技术学院, 北京　100083)



Triangle软件在自适应剖分中的应用

张衍林，梅钢，徐能雄

(中国地质大学(北京) 工程技术学院, 北京100083)

摘要：大型商业CAE/CAM软件价格昂贵、操作复杂，且在生成大规模三角网格时速度较慢。Triangle软件是一个开源、功能强大、操作简单的二维三角网格生成器。该软件能根据边界的复杂程度，极其高效地生成高质量的、自适应的三角网格，但是该软件在国内应用较少。阐述了利用该软件进行网格自适应剖分的步骤，并通过工程实例对采用不同剖分方法得到的网格进行质量对比和数值计算。结果表明：Triangle软件操作简单、实用性强；采用由加密区向非加密区过渡的自适应剖分方法，产生的单元质量较好，且计算效率和精度可以达到实际工程中数值计算的需要，值得在数值模拟领域推广应用。

关键词：Triangle软件； 自适应网格； 三角剖分； 数值计算； 效率

随着计算机技术的普及和发展，为了更准确、真实地反映研究对象，人们对数值分析的复杂程度、效率和精度方面有了更高的要求[1]。据统计，在数值分析的3个阶段中：前处理约占总时间的40%～60%；数值求解约占5%～20%；计算结果后处理约占30%[2]。如果对复杂的分析区域进行人工布点、离散，工作繁杂，且容易出错。此外，在数值计算中，需要根据应力、应变的大小设置网格加密区和非加密区，为实现网格的平稳过渡，也需要使用网格自动加密的自适应剖分方法，准确地表现出分析对象的几何特征。

Delaunay三角网具有空外接圆性质和最大的最小角性质，是“最接近于规则化”的三角网[3]。目前很多学者对Delaunay剖分进行了优化，如将凸包法、逐点插入法、角度判别对角线法相结合[4]，对平面点集使用并行二维凸壳算法[5]，将无约束的Delaunay三角剖分与带断层约束的Delaunay三角剖分结合使用[6]，对各种平面、空间点云数据采用局部连接Delaunay边、Delaunay 面的方法[7]，实现了高效率、高精度的Delaunay三角剖分。据此很多学者以Delaunay三角剖分为基础，编制出网格剖分软件，如北京大学研制的 AUTOMESH 软件，可保证网格剖分的收敛，且剖分结果最优[8]。EasyMesh[9]是简单易用的二维三角形网格产生器，能对折线围成的多空洞、多介质区域进行局部加密的三角形剖分。Gmsh[10]和TetGen[11]能快速生成三维的高质量网格，在国外的应用较广。

Triangle软件能进行Delaunay三角剖分和限定Delaunay三角剖分，具有高效率自适应剖分的强大优势，但是在现阶段介绍该软件的文献较少。因此，本文介绍了Triangle软件的功能及使用步骤。实例验证结果表明：使用该软件进行自适应剖分产生的网格质量较高，计算速度和计算精度满足数值模拟的需要，对于提高数值分析前处理阶段的工作效率和促进该软件在网格自适应剖分中的应用具有重要意义。

1　Triangle软件介绍

Triangle软件是由加州大学伯克利分校Jonathan Richard Shewchuk教授编制的、以C语言为基础的、在Linux操作系统下运行的平面三角剖分软件，特别适用于以二维模型为基础的数值模拟计算。与大型商业CAE/CAM软件相比有如下优势：

1.1软件规格小，操作简单

Triangle软件大小不足1M，无需安装，只需将代码文件置于Linux操作系统下，通过gcc编译器编译运行即可。操作命令是由研究区域的数据文件名和控制不同剖分方法的开关组合构成的，通过输入一行命令即可实现剖分。

现有的大型商业CAE/CAM软件集建模与计算功能于一体，规格动辄1G，安装步骤复杂，且不易成功；由于版权限制，使用这些软件时需要付费购买；当使用此类软件建模时，大多数需要通过手工绘制模型，对于边界复杂区域只能简化模型，影响数值计算精度。

1.2软件功能强大，剖分速度极快，剖分单元质量好

Triangle软件能对点集和平面区域进行剖分和二次剖分，生成高质量网格。该软件能接受用户自定义的约束条件，如角度和三角形面积，可对“洞”和“凹、凸”等实现网格剖分[12]。该软件剖分时占用内存小，剖分时间以毫秒计算，可以根据边界形状添加节点和加密网格，实现单元的自适应剖分和由加密区到非加密区的平稳过渡。

现有的大型商业CAE/CAM软件可以对体和壳进行剖分。但是当对复杂边界进行自适应剖分和网格由加密区到非加密过渡时，需要在边界处重新布点，操作步骤较为复杂，剖分时占用内存较高，剖分速度相对较慢。

2　Triangle软件的应用

Triangle软件的使用流程分为输入模型数据文件、剖分、输出数据文件3步。其中输入文件就是通过提取出构成模型所有线段的起点坐标和终点坐标，制作出Triangle软件可以识别的环文件；剖分就是选择代表不同剖分方法的开关，通过限制三角形单元的角度或面积实现网格的生成；输出的数据文件为网格的节点文件和单元文件。

2.1输入数据文件

Triangle软件进行网格剖分所针对的模型是由若干闭合环组成的。图1中共有2个闭合环，环上有12个节点，环内部有1个指示点。指示点是表征孔洞位置的点，即包含指示点的最小环为孔洞。将图1中所有点和线段的信息进行整理生成环文件，作为Triangle软件的输入文件。

图1　原始模型

将图1中所有点和线段的信息整理生成名为example1.poly的环文件，具体内容如下：

# 以“#”开头的行是注释行

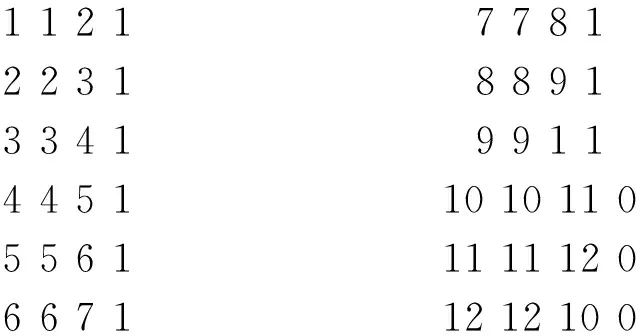
# 线段总数 边界符号

# 孔洞数目

1

# 孔洞ID 指示点x坐标 指示点y坐标

1 65 68

2.2剖分

Triangle软件是在Linux系统下运行的，因此需要将Triangle软件的源代码放在名为Code的文件夹下，并将该文件夹放在系统主目录Home文件夹下。通过在终端输入cd Code命令索引源代码，并分别输入“gcc triangle.c-lmo triangle”和“./triangle”命令来编译、运行软件，显示软件的功能开关，如图2所示。该软件主要是借助不同开关的相互组合实现不同的剖分效果。

对图1所示的模型，通过在终端输入“./triangle-pqa43.3 example1.poly”命令进行网格剖分，结果如图3所示。

图2　Triangle软件运行界面

图3　Triangle软件剖分完毕界面

2.3输出数据文件

如图3所示，剖分完成之后产生新的节点文件、单元文件、环文件，并提示网格由53个节点和72个三角形单元组成。将点文件和单元文件进行整合，输入到第三方数值分析软件中生成网格，如图4所示。

图4　生成的网格

3　应用实例

3.1工程概况

某矿山地上部分的矿产已基本开采完毕，即将转入井下开采。取该区域某一地质剖面作为地质模型的初始资料。如图5所示，地表有约20 m厚的第四系覆盖层，南坡主要为混合岩，北坡主要为千枚岩，中间区域为铁矿石。

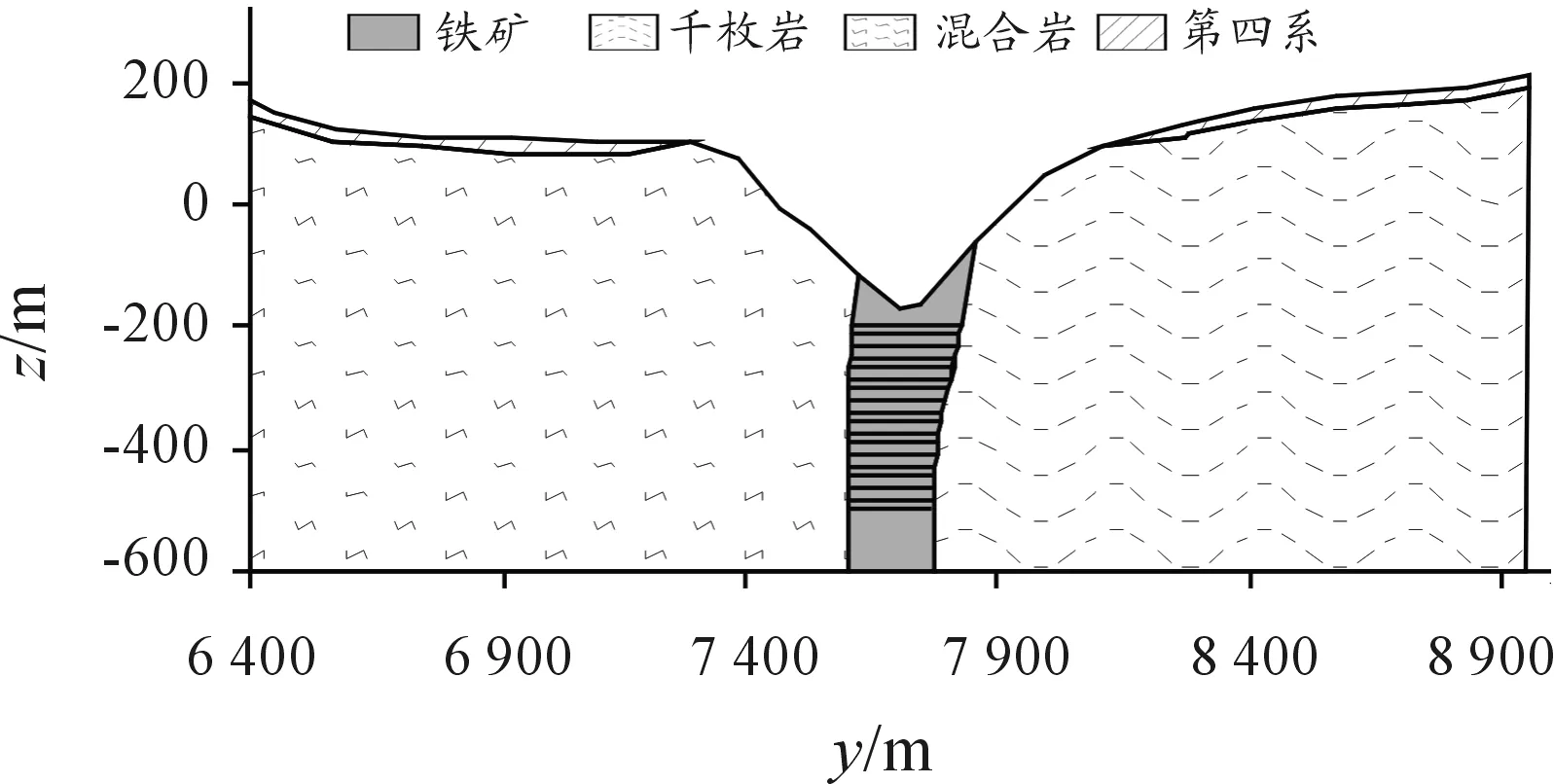
图5　矿山开采地质剖面

随着开采深度的增加，将会在矿井两侧形成高边坡，为保证生命财产安全和矿产的顺利开采，需要对边坡的变形情况进行研究。岩体的物理力学参数如表1所示。

表1　岩体物理力学参数

3.2网格剖分

网格大小主要根据数值计算需要的精度来确定。随着矿产开采深度的增加，边坡潜在滑动面与临空面之间的的岩体应力和应变较为显著。为提高数值计算精度，需要对该区域的单元进行加密。根据其他区域是否进行加密或者加密区与非加密区之间过渡方式的不同，主要有以下3种剖分方法:

1) 模型整体加密剖分

此次研究中,使用腹腔镜检查,有47例子宫浆膜下肌瘤,10例盆腔粘连,18例输卵管堵塞,17例卵巢囊肿,14例子宫穿孔和肿块。有46例轻度疼痛,49例中度疼痛,11例有迷走神经刺激症状。患者平均手术花费24.5 min,平均出血31.5 m L。对患者患者了半年的随访,有2例失联,共有40例子宫浆膜下肌瘤患者月经正常,7例改善。10例盆腔粘连患者接受分离手术后,子宫形态恢复,内膜生长良好。有17例卵巢囊肿患者症状改善。有12例输卵管堵塞的患者均成功妊娠,有3例疏通。

将图5中的模型整理生成名为example2.poly的环文件，通过在在Linux系统终端输入“./triangle -pqa7 example2.poly”命令，将图5中的全部区域剖分成单元面积不超过7 m2的网格，如图6所示。将网格名称命名为a，该网格共有节点196 513个、三角形单元391 354个。

图6　整体加密剖分网格图

2) 网格由加密区向非加密区自由过渡

为减少单元数量，对于应力、应变不显著区域不进行单元加密，即为非加密区。根据经验估算，当开采矿层至最后一层时为最危险滑动面的位置。在图5中添加辅助线，即图7中的粗虚线，该虚线将剖分区域分为加密区和非加密区。对于非加密区，不限制单元大小，在拓扑关系一致的前提下，Triangle软件自由添加节点，实现自适应剖分。

将图7中的模型整理生成名为example3.poly的环文件，在Linux系统终端输入“./triangle-pqa example3.poly”命令，将图7中的粗虚线以内的区域剖分成单元面积不超过7 m2的网格，其他区域的网格根据拓扑关系一致的原则自由过渡，最后生成的网格如图8所示。将网格名称命名为b，该网格共有节点34 668个、三角形单元68 930个。

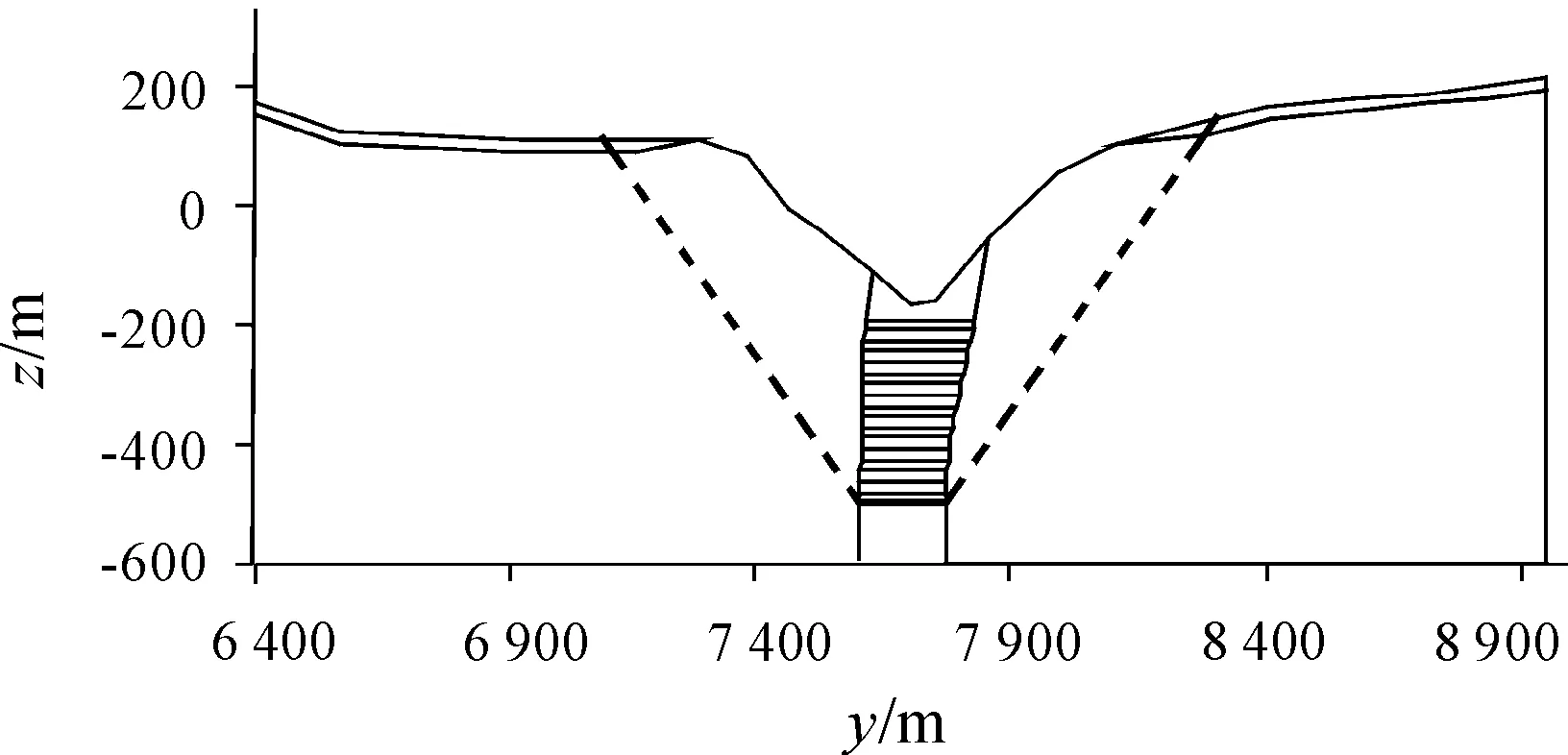
图7　自由过渡模型

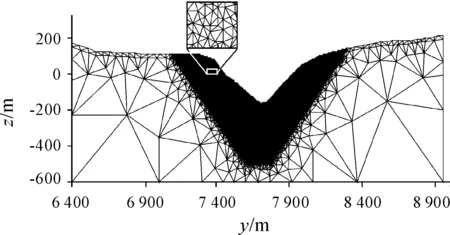
图8　自由过渡网格

3) 网格由加密区向非加密区稳定过渡

图8中从加密区到非加密区单元大小变化太大。为实现单元的稳定过渡，对非加密区人为分成多个小区域，并限制每个小区域的单元大小，在拓扑关系一致的前提下，对非加密区实现自适应剖分。在图7中添加细虚线作为辅助线，如图9所示。

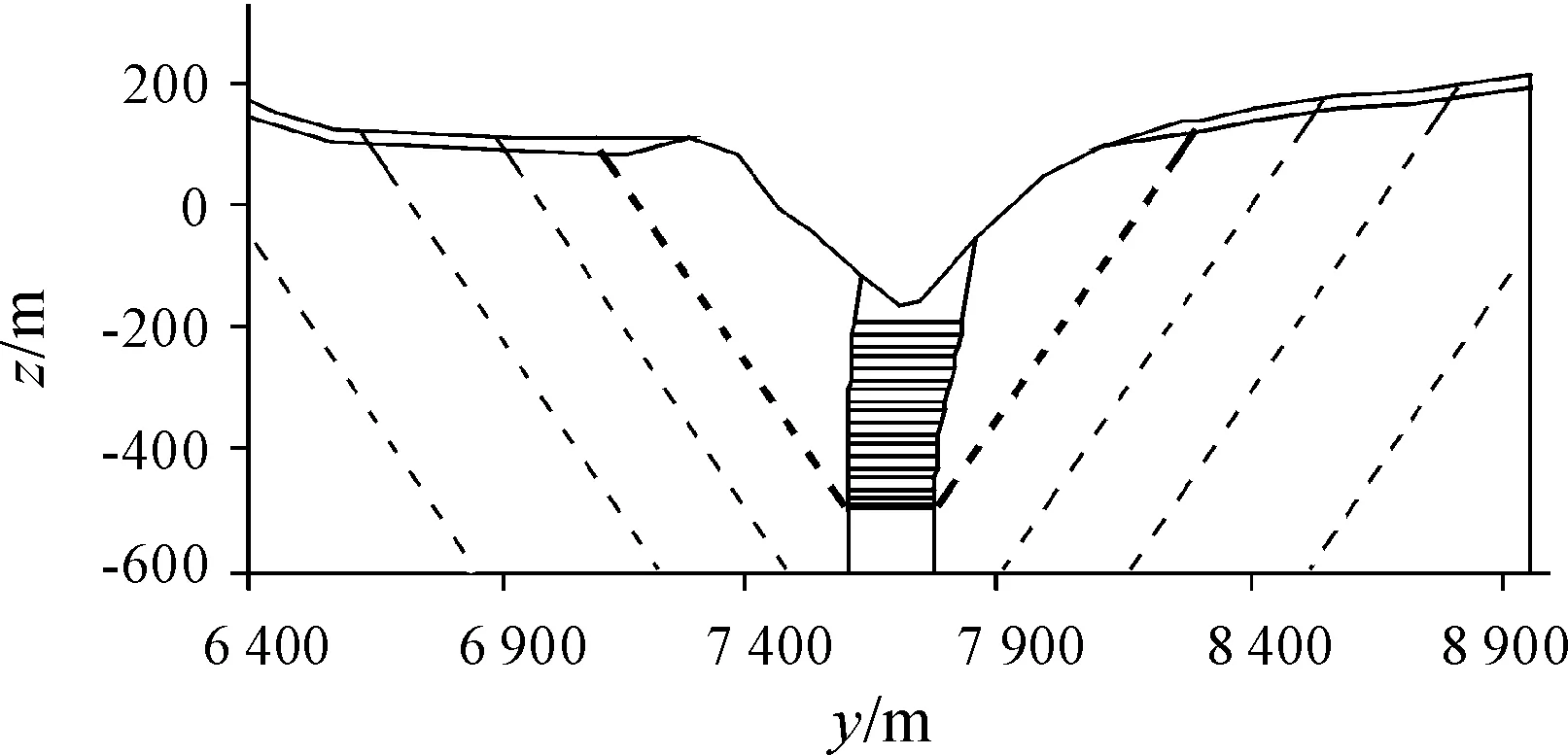
图9　稳定过渡模型

将图9中的模型整理生成名为example4.poly的环文件。在Linux系统终端输入“./triangle-pqa example4.poly”命令，将图9中的粗虚线以内的区域剖分成单元面积不超过7 m2的网格，其他区域的单元面积最大值以加密区为中心向两边逐渐过渡，依次为43.3，173.2，530.425，1 082.5 m2，如图10所示。将网格名称命名为c，该网格共有节点42 846个、三角形单元85 104个。

图10　稳定过渡网格图

将a、b、c三种网格的信息进行整理，结果如表2所示。

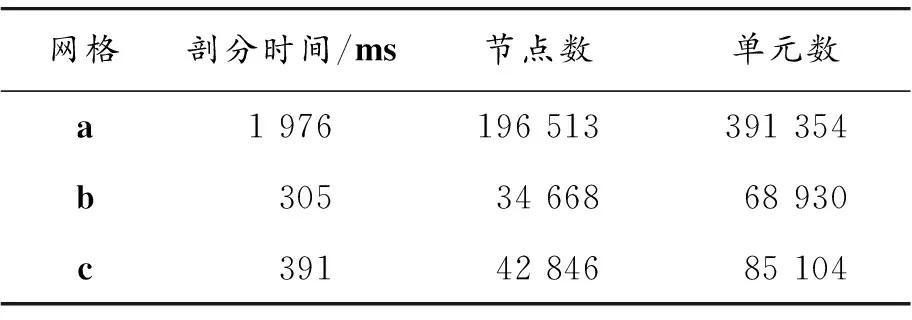
表2　网格剖分情况统计

图6与图8对比，对非加密区进行网格剖分时，前者存在单元面积限制，Triangle软件自动在边界添加节点，后者无单元面积限制，边界上节点明显较少。图8与图10对比，后者通过添加多条辅助线，限制非加密区网格剖分时内部节点的位置，实现网格的平稳过渡。

3.3网格质量

二维单元的主要质量指标包括单元长度、翘曲角、单元边长比、内角大小、扭曲角、雅可比比率等[13]。根据LEE C K和LO S H[14]提出的评价三角形质量的公式(式(1))评价Triangle剖分后每一个三角形的质量。

(1)

其中AB是以三角形顶点A为起点，以顶点B作为终点的向量，AC、BC亦如此。

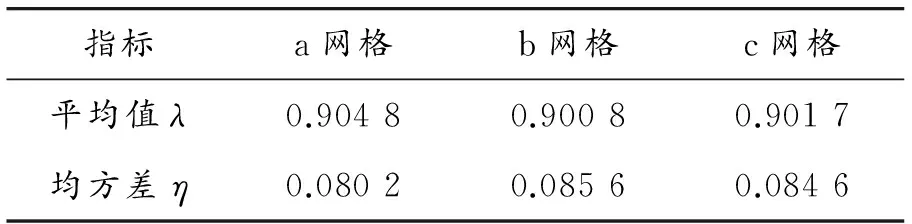
根据平均值公式和均方差公式(式(2)和(3))计算上述3种网格质量的平均值和均方差值，结果如表3所示。

(2)

(3)

式(1)中α值范围为0～1，单元质量随着α值的增大而变好。对表3中的平均值λ和均方差值η做对比发现：a网格质量最好；b网格质量最差；c网格质量居中。

3.4数值计算

将剖分之后的网格沿x轴方向拉伸20 m，模型由二维转变成拟三维，三角形单元转变成三棱柱单元。将模型导入FLAC3D软件中进行数值计算，验证不同的剖分方法对计算效率和计算精度的影响，以此选择最佳的剖分方式。为表述方便，a、b、c网格拉伸后的模型分别命名为a-a、b-b、c-c模型，其中c-c模型如图11所示。

图11　FLAC3D中c-c模型

数值计算采用位移约束边界条件，对侧面施加法向位移约束，对底面施加全约束，采用摩尔-库伦本构关系，重力加速度取值为9.80 m/s2，开挖第1层矿产。当计算不收敛时，即出现塑性区贯通时，停止计算。a-a、b-b、c-c模型数值计算结果分别如图12～14所示，图中A、B点为最危险滑动面在地表的位置。

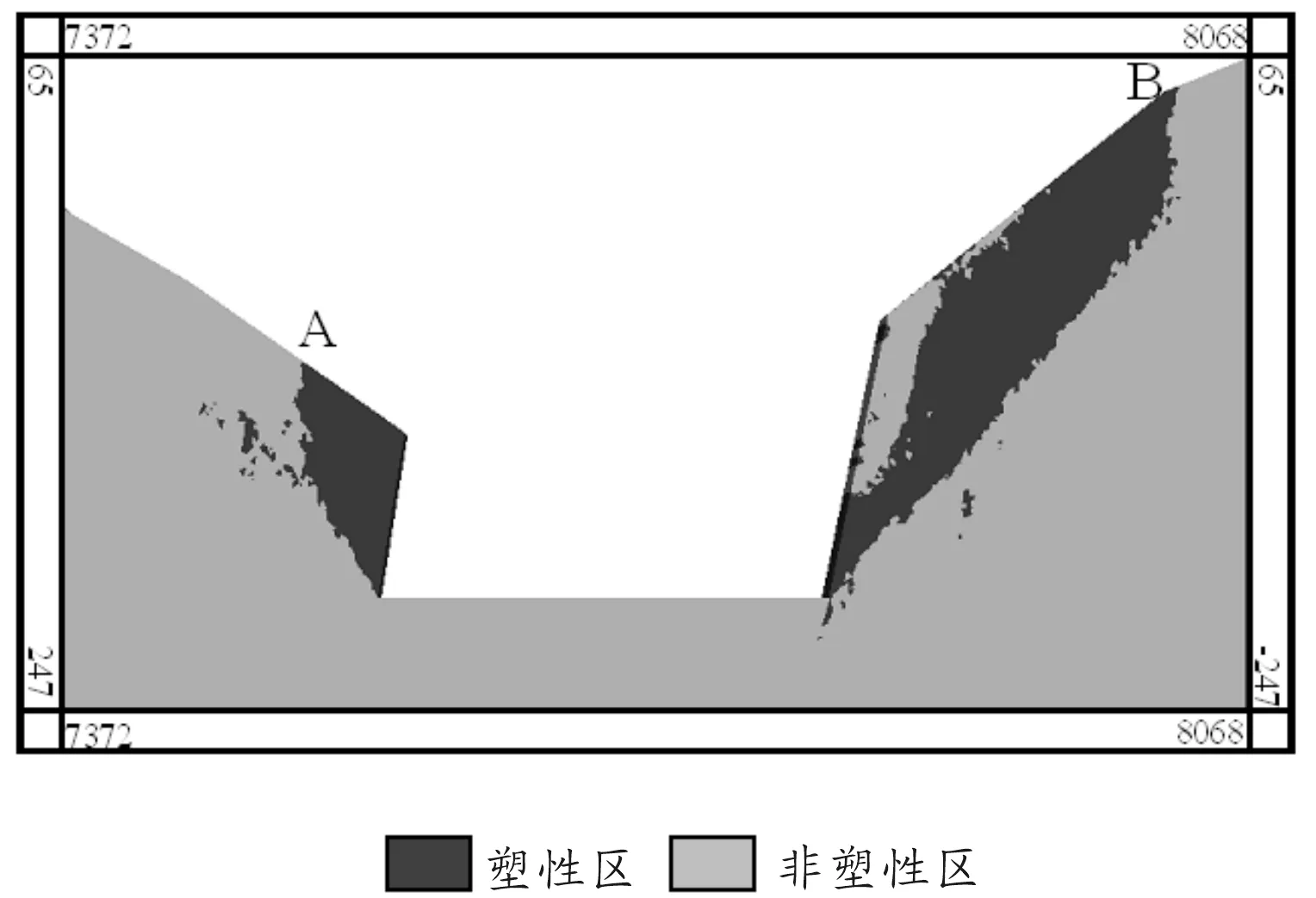
图12　整体加密塑性区图

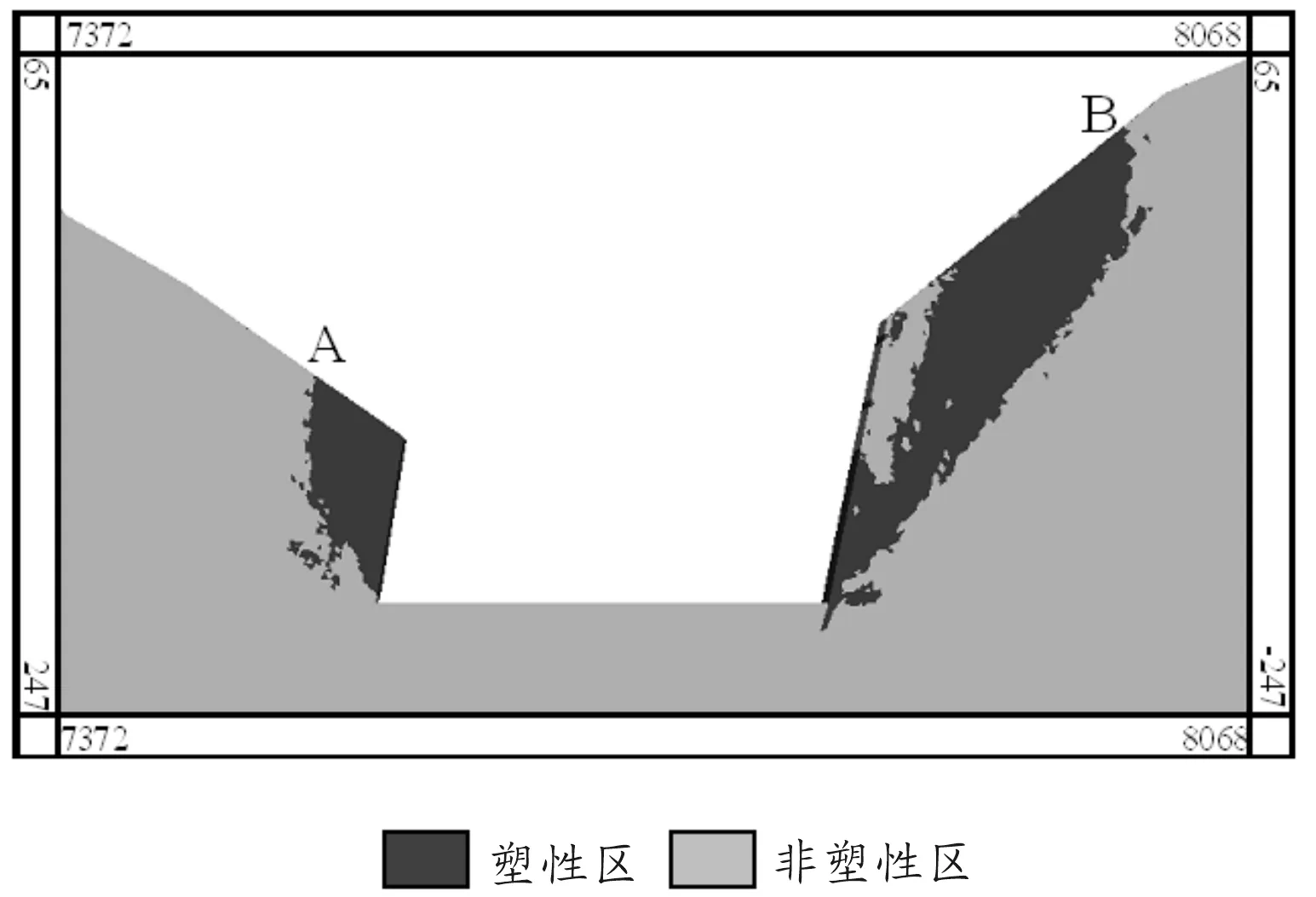
图13　自由过渡塑性区图

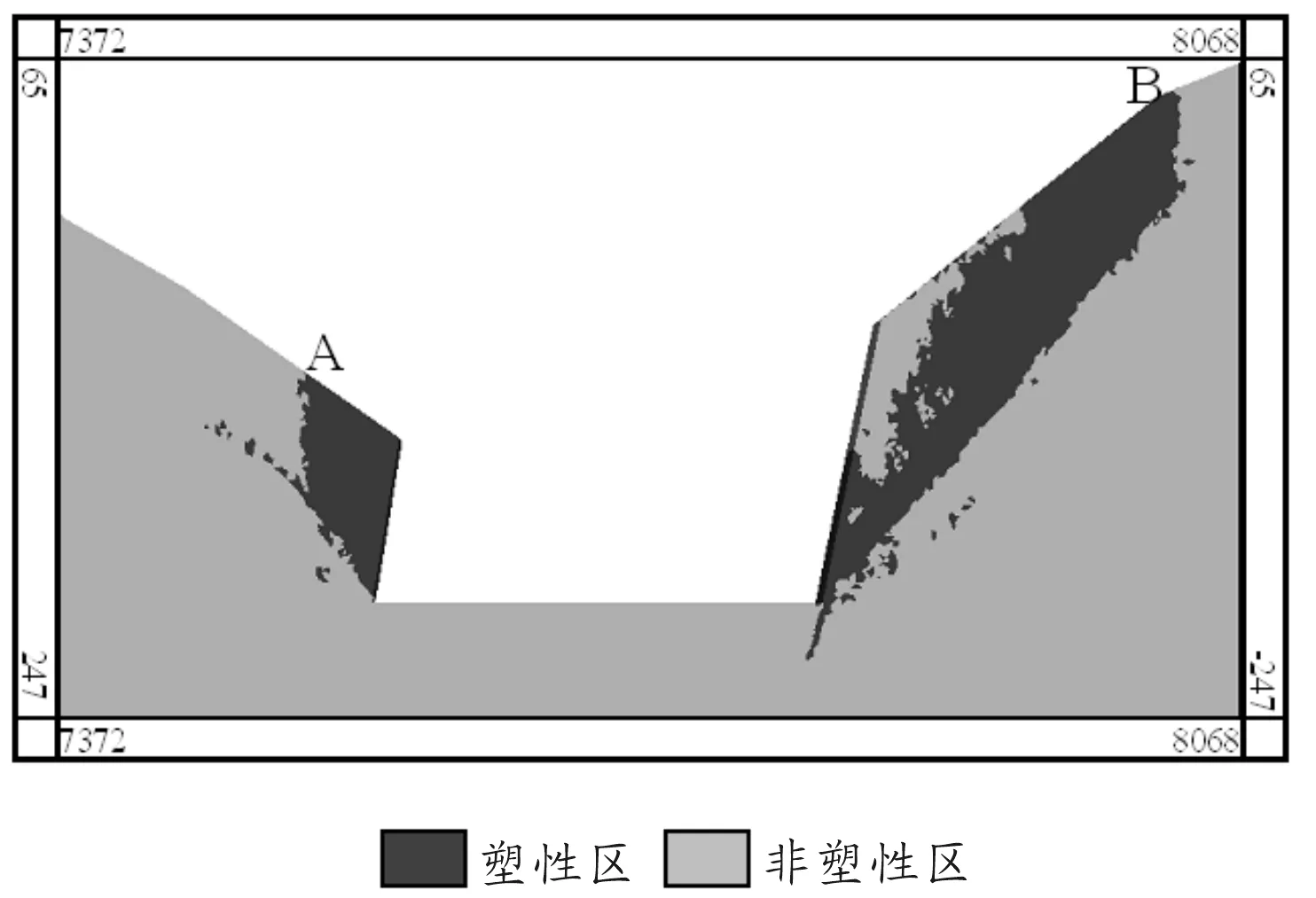
图14　稳定过渡塑性区图

将计算时间和最危险滑动面在地表的位置分别作为计算效率和计算精度的判断依据。计算精度是通过塑性区范围确定的，如果计算得到的范围偏小，则存在安全隐患，计算精度偏低。统计结果见表4。

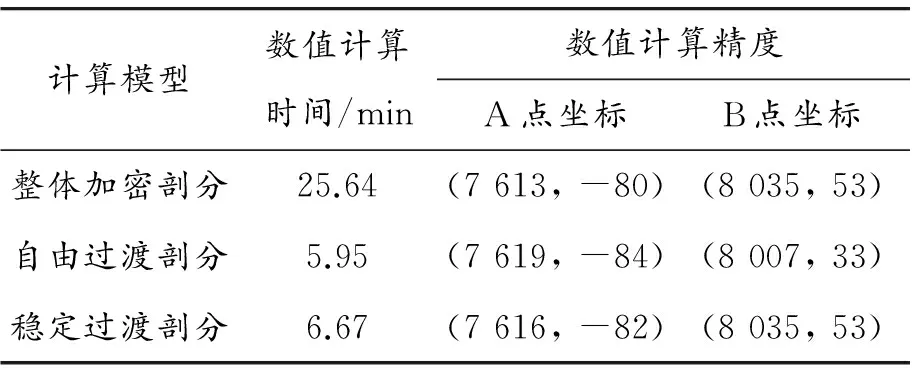
表4　数值计算结果统计

由图12～14及表4可以得出：a-a、b-b、c-c 模型进行数值计算的时间关系为a-a>c-c>b-b；精度关系为a-a>c-c>b-b。

将表2、表3、表4进行对比分析得出：c网格剖分用时、单元数和节点数均小于a网格；c网格单元质量高于b网格；c-c模型数值计算效率和精度均优于b-b模型。因此采用稳定过渡的自适应剖分是一种较为合适的剖分方法。

4　结论

Triangle软件是一款高效的二维剖分软件，规格小、操作简单，其优势完全能与大型商业软件拥有的前处理功能媲美。

1) 该软件能根据边界的复杂程度进行自适应剖分，自动添加节点、加密网格，实现网格由加密区到非加密区的稳定过渡。

2) 该软件对大规模网格剖分用时较短，剖分形成的网格总体质量较好，将模型导入数值计算软件后计算时间较短、精度较高。

虽然该软件具有强大的剖分功能，但是仍有不足之处，影响该软件的推广使用。该软件通过输入代表模型信息的环文件进行网格剖分，当地质情况复杂时，尤其模型中点的数量较多时，难以手工制作环文件，需要通过自己编制程序处理数据。因此建议开发出通过输入CAD模型直接生成Triangle软件可以识别的环文件的程序，从而提高生成数值计算模型的效率。

参考文献：

[1]SHEWCHUK J R.Triangle:Engineering a 2D quality mesh generator and Delaunay triangulator[C]//Applied computational geometry towards geometric engineering.Berlin Heidelberg:Springer,1996.

[2]SHEPHARD M S.Approaches to the Automatic Generation and Control of Finite Element Meshes[J].Applied Mechanics Review,1998,4(4):169-185.

[3]郭光毅,王新生,李朋泽,等.基于Delaunay三角网的多边形特征点提取方法[J].地理空间信息,2014(4):124-126.

[4]余代俊,蒲朝旭,朱逍贤.一种Delaunay三角剖分的改进算法[J].测绘通报,2014(6):51-54.

[5]毕硕本,陈东祺,颜坚,等.维凸壳的平面点集Delaunay三角网算法[J].计算机科学,2014(10):317-320.

[6]张群会,解子毅.带断层约束的Delaunay三角剖分混合算法[J].西安科技大学学报,2014(1):52-56.

[7]姜元政,高福顺,王浩杰,等.点云数据三角网格生成算法及应用[J].北华大学学报(自然科学版),2014(3):314-317.

[8]孙璐.基于栅格法的三维六面体网格自适应生成算法及优化技术研究[D].济南：山东大学,2012.

[9]NICENO B A.Two-Dimensional Quality Mesh Generator[EB/OL].[2014-10-30].http://www-dinma.units.it/nirftc/research/easymesh/easymesh.

[10]GEUZAINEC，REMACLEJF.Gmsh:athree-dimensionalfiniteelementmeshgeneratorwithbuilt-inpre-andpost-processingfacilities[J].InternationalJournalforNumericalMethodsinEngineering,2009,79(11):1309-1331.

[11]HANGS.AQualityTetrahedralMeshGeneratoranda3DDelaunayTriangulator[EB/OL].[2014-10-30].http://wias-berlin.de/software/tetgen/.

[12]吴莉莉.Triangle的稳定化与地理应用[D].北京：华北电力大学,2012.

[13]李海峰,吴冀川,刘建波，等.有限元网格剖分与网格质量判定指标[J].中国机械工程,2012(3):368-377.

[14]LEECK，LOSH.Anewschemeforthegenerationofagradedquadrilateralmesh[J].ComputersandStructures,1994,52(5):847-857.

(责任编辑杨文青)

收稿日期：2016-02-18

基金项目：国家自然科学基金资助项目(40602037，40872183)

作者简介：张衍林(1988—)，男，河北石家庄人，硕士研究生，主要从事地质工程数值模拟方面的研究。

doi:10.3969/j.issn.1674-8425(z).2016.07.019

中图分类号：TP319

文献标识码：A

文章编号：1674-8425(2016)07-0112-07

Application of Triangle Packge in Adaptive Mesh Generation

ZHANG Yan-lin, MEI Gang, XU Neng-xiong

(School of Engineering and Technology,China University of Geosciences (Beijing), Beijing 100083, China)

Abstract:Large commercial CAE/CAM software is typically quite expensive; and the operations in the use of the large software are in general complex. In addition, the computational efficiency in the cases of generating large-scale triangular meshes is low. The package triangle is an open source, powerful, easy-to-use 2D triangular mesh generator. This package has the capability of producing high-quality adaptive triangular mesh extremely fast for the target regions that are represented with complex boundaries. However, there are few references published in China that are focused on introducing the applications of this package. This paper first described the detailed steps of employing this package for generating high-quality adaptive meshes, and then presented a real-world engineering application to demostrate the effectiveness and efficiency of this package. The application results indicate that: the package triangle is effective and easy to use; It uses adaptive subdivision method to make the transition from encryption area to the non-encryption section, through which the unit quality is better; in addition, the computational efficiency and accuracy when using the high-quality adaptive triangular meshes can reach the requirements in practical numerical applications.

Key words:Triangle software; adaptive mesh; triangulation; numerical calculation; efficiency

引用格式：张衍林，梅钢，徐能雄. Triangle软件在自适应剖分中的应用[J].重庆理工大学学报(自然科学)，2016(7):112-118.

Citation format：ZHANG Yan-lin, MEI Gang, XU Neng-xiong.Application of Triangle Packge in Adaptive Mesh Generation[J].Journal of Chongqing University of Technology(Natural Science)，2016(7):112-118.