城市生活污水处理的生物建模与控制策略研究

邓新莉，刘　珊

(1.重庆广播电视大学，重庆　400052； 2.重庆汉锦科技公司，重庆　400010)



城市生活污水处理的生物建模与控制策略研究

邓新莉1，刘珊2

(1.重庆广播电视大学，重庆400052； 2.重庆汉锦科技公司，重庆400010)

摘要：为了克服由于受变量多、不确定性等因素影响导致的生活污水处理难于实现优化控制的问题，探讨了生活污水处理的生物建模与控制策略。讨论了污水生物处理工艺与反应机理，构建了生化反应动力学模型，研究了反应过程的控制论特性，提出了与控制论特性匹配的控制策略。经实验仿真验证基于溶解氧浓度DO控制的智能控制策略可自动跟踪污水处理溶解氧浓度的期望状态。研究结果表明：智能控制可以较好地实现城市生活污水处理的优化控制，该控制策略可行、有效。

关键词：活性污泥法；污水生物处理；溶解氧控制；优化控制

在物理、化学和生物等3种污水处理方法中，生物处理方法因其可人工模拟自然水体自净过程倍受关注。在常见的污水处理工艺中，用得最多的是SBR工艺(sequencingbatchreactoractivatedsludgeprocess)，即序列式活性污泥法工艺。该工艺集曝气池和污泥沉淀池于一身，既能降低基建费用和运行成本，也有利于运行管理与自动监控，还可借助调节每个工序时间达到脱氮除磷的目的。SBR已成为国内外普遍采用的主导型工艺，很多文献[1-7]对此都进行了研究。其中：文献[4]研究了城市生活污水处理过程控制与优化问题；文献[5]研究了污水处理工艺设备系统模型并进行了仿真研究；文献[6-7]分别对缺氧-好氧活性污泥法数学模型和活性污泥数学模型进行了专题研究。污水微生物处理是一个具有不确定性的复杂过程，为了提高污水处理效果，有必要对生活污水处理的控制策略做进一步研究。

1　数学模型与SBR法工艺仿真

1.1生化反应数学模型

序列式活性污泥法工艺运行图如图1所示。图2是SBR的工艺示意图。图2中，瀑气池就是一个生物反应器。由于SBR法采用周期性运行方式，生物反应过程具有高度的时变性、非线性和不确定性等特点，因此只能在一定假设条件[8]下建立其生化反应动力学数学模型。在反应池内其假设条件为：物质只存在一个反应阶段内；物质浓度是均匀混合的；污染物均为可溶的有机物质，可被微生物分解；微生物生长率大于其死亡率，并且满足Monod方程；二级沉淀池内只有物理沉淀过程，不存在生化反应。

图1　SBR工艺运行图

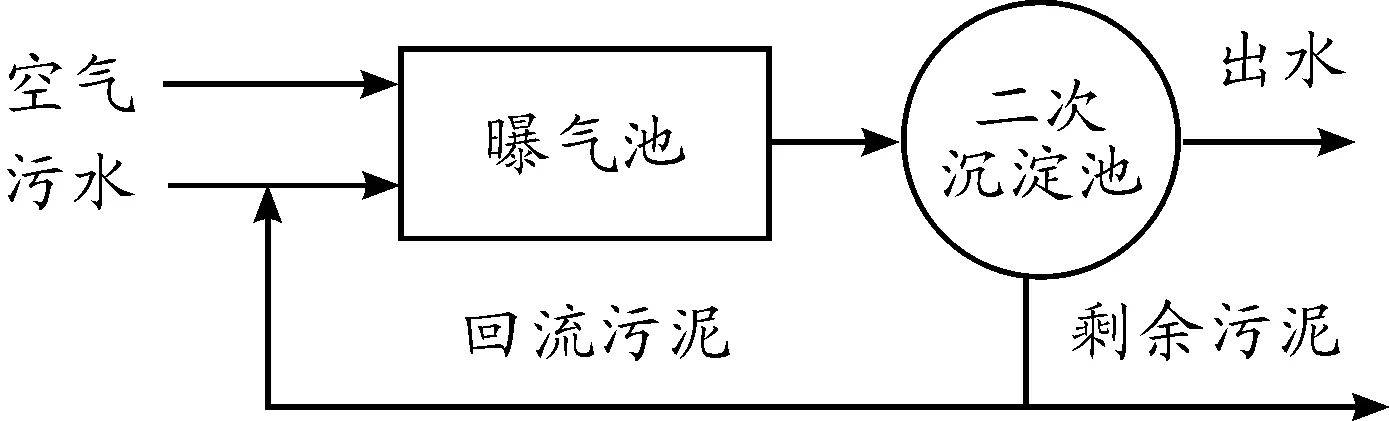
图2　SBR工艺示意图

1) 微生物浓度变化模型

在污水处理过程中，不同种类的微生物其生长速率不同，且微生物必须维持在一定数量之上，以确保生化反应的正常进行。微生物浓度变化与多种因素有关，通常采用莫诺特(Monod)模式建模[9]，污染物浓度S与单位微生物生长率μ的关系如式(1)所示。

(1)

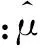
工程实验表明：当溶解氧DO浓度趋近于0时，μ也几乎为0，与S无关；当DO浓度达到饱和系数KO时，μ将变成常数。这种现象可在通过式(1)中加一个开关函数加以描述，见式(2)。

(2)

由μ定义可知：

(3)

由于微生物消耗速率与微生物本身的数量成正比，如微生物衰减系数为Kd,则有

(4)

按照质量平衡原理可得：

(5)

即

(6)

将式(2)～(4)代入式(6)，即可得到如式(7)所示的微生物浓度变化模型。

(7)

2) 有机物去除过程模型

生化反应过程如式(8)所示。如果用Y表示微生物生产率系数，则其生化反应过程中新生长的微生物量如式(9)所示。

(8)

(9)

由物理概念可知：反应池中污染物浓度变化可用式(10)表示。

(10)

事实上，在有机物去除的过程中，异养微生物在衰亡过程中也需要消耗一部分有机物。设惰性组分为 fP，则污染物浓度变化为

(11)

综合上述，污染物浓度变化的数学表达式为

(12)

3) 溶解氧浓度变化模型

在污染物降解过程中，溶解氧浓度的变化可表示为

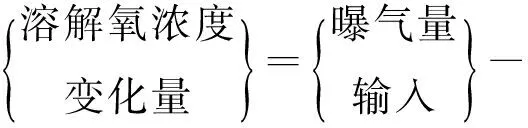
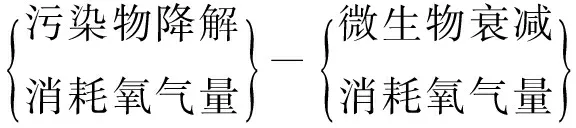
(13)

由生化反应过程式(8)和新生长的微生物量式(9)可知：其溶解氧消耗速率为

(14)

在曝气过程中，由文献[10]可知：经过推导，溶解氧浓度变化的数学模型可表示为

(15)

式中：SO，sat为溶解氧饱和浓度；SO为溶解氧浓度； KL·α为与空气流量有关的系数。

综合上述微生物浓度、有机污染物去除浓度和溶解氧浓度变化的数学模型，可以得到采用SBR法处理污水过程的数学模型：

(16)

由式(16)可见：各变量之间的关系至少是强关联耦合和强非线性的，并且是在一定假设条件下推导得出的。

1.2SBR法工艺仿真

SBR法去污原理：污水中的异养微生物自身生长必须摄取污水中的溶解氧DO和有机污染物，在生化作用反应下去除污水中的有机污染物。在该生态系统中，异养微生物只能依靠污水中现成的有机养料存在，而不能自己制造有机养料，因此在生化反应过程中，使得污水中的有机污染物不断降解。显然，如果能借助工艺仿真，找出底物浓度、异养微生物浓度与溶解氧DO浓度之间的变化规律可为改进去污效果提供指导。现以文献[11]提供的数据为例，在Matlab2010Ra环境下，基于数学模型式(16)对底物浓度、异养微生物浓度与溶解氧DO浓度之间的关系进行仿真研究。在改变DO浓度参数时，底物和微生物浓度随时间变化的曲线如图3、4所示。

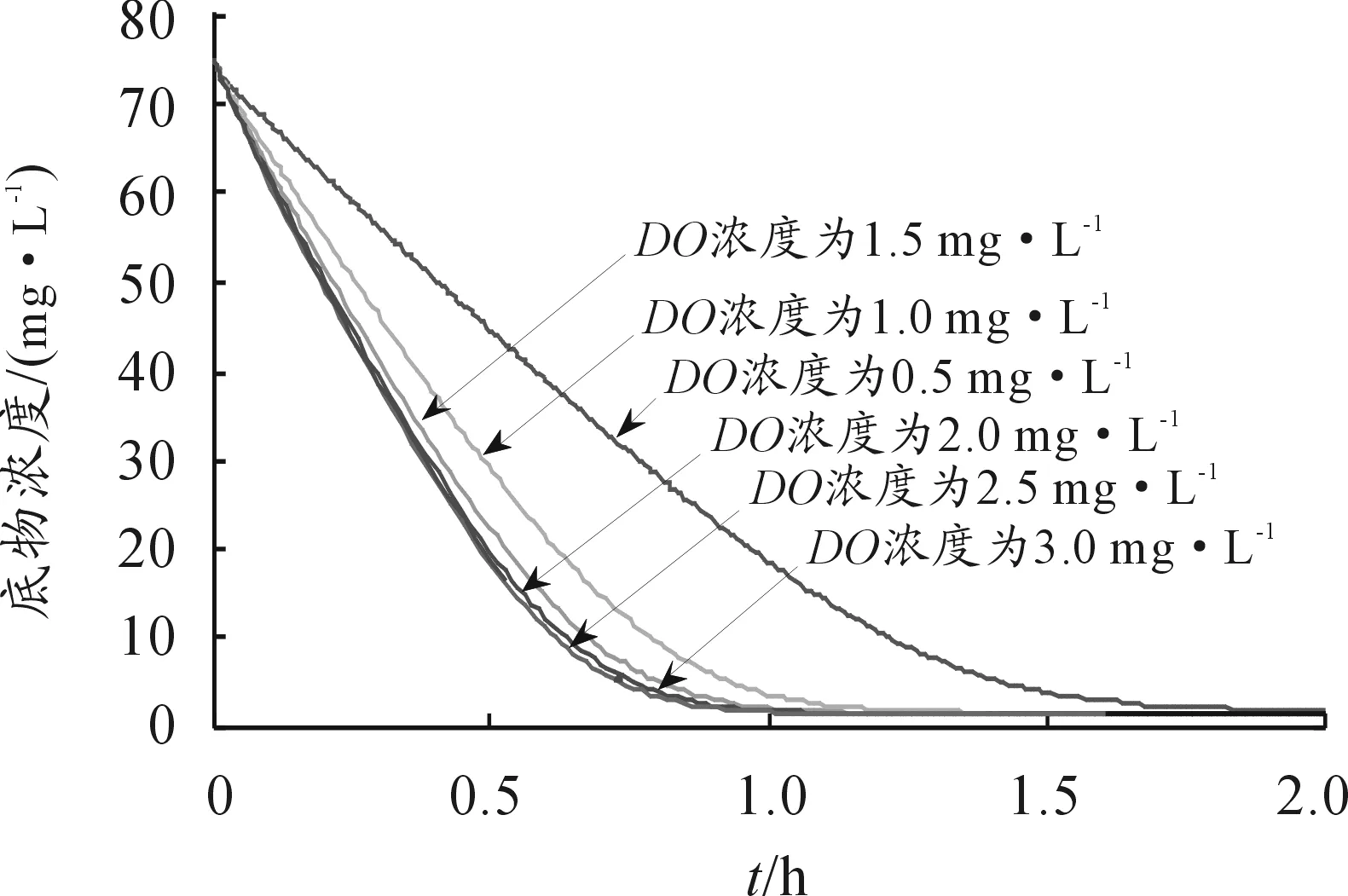
图3　污染物浓度变化曲线

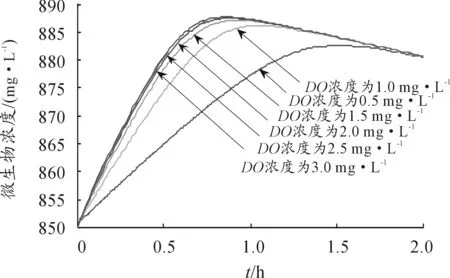
图4　微生物浓度变化曲线

图3表明：控制DO浓度可实现污水中污染有机质的降解，DO浓度不同，有机质降解的能力也不同。当DO浓度大于2.0mg/L时，底物降解能力提升减弱；当DO浓度小于2.0mg/L时，底物降解能力明显增加；而当DO浓度等于2.0mg/L时，其降解效果最佳。

图4表明：DO浓度可控制微生物净生长率提升，但当达到一定微生物浓度时，微生物净生长率不再随时间而改变，其微生物的生成将保持恒定值；当DO浓度等于2.0mg/L时，微生物生长率效果较好。如图5所示，DO浓度在污水处理过程中是变化的，为使其恒定保持在2.0mg/L，以获得更好的污水处理能力，必须设计性能良好的控制器对DO浓度进行控制，以达到最好的污染物降解效果。

2　污水处理过程的控制论特性

上述生化过程数学模型是在若干假设条件下得出的。生物污水处理方法是借助异养微生物摄取污水中的溶解氧DO和有机污染物去除污水中的有机质污染物。这里，溶解氧DO浓度是可控的，至于采用什么策略对溶解氧DO浓度进行控制与生化反映过程的控制论特性紧密相关，其控制论特性[12-13]主要表现在：

1) 生化过程的不确定性

传统控制通常假定其模型本身就是已知。事实上，生物污水处理过程具有极大的不确定性，其模型是在若干假设条件下得出的，生化反映机理极其复杂。比如污水组分随时随地都可能不同，人们对此难以预料。对于这类“未知”并具有不确定性的问题,所建数学模型只能为控制策略的选取提供参考。因此，以污水过程的数学模型为依据设计的控制器难以达到预期的控制效果。

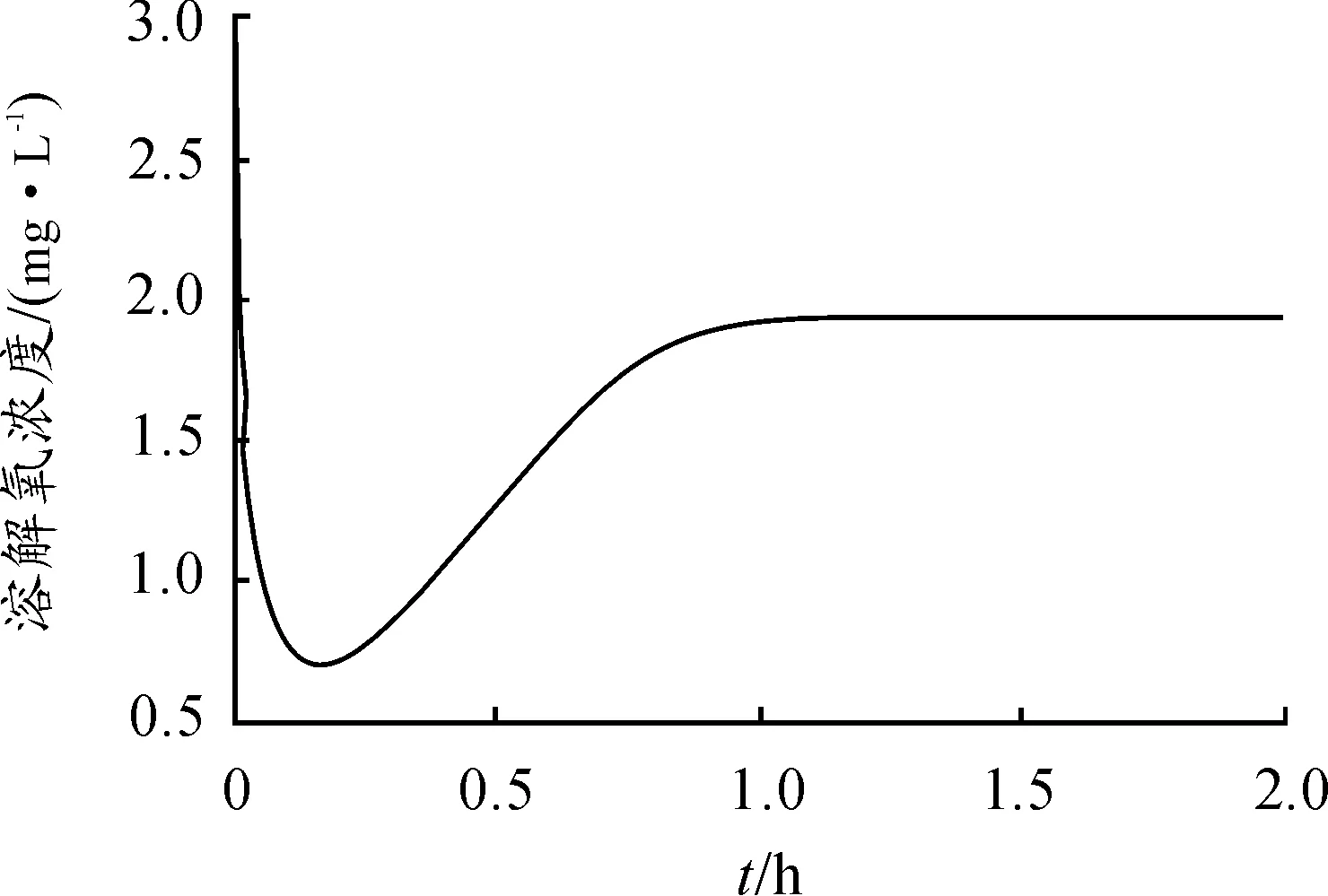
图5　DO浓度变化曲线

2) 生化反应过程的高度非线性

污水处理过程中，参加生化反应的底物、异养微生物与溶解氧DO浓度之间存在高度的非线性关系，其变化规律很难采用线性化方法描述。因此，传统控制中的非线性处理方法在控制系统设计中难以应用，传统控制方法对此几乎无能为力。

3) 半结构化与非结构化

生化反应过程是半结构化与非结构化的，即使是在预先假定条件下导出的动力学数学模型中，各个变量之间的关系也是强关联耦合的，难以实现严格意义上的解耦控制。因此，将传统控制方法用于控制污水处理过程不可取。因传统控制属定量控制范畴,传统控制方法在本质上是一种数值计算方法。

4) 过程复杂性

在生化反应过程中，外部环境复杂多变,各控制要素之间关系错综复杂,且呈现随机性、分散性、时变性、多样性、未知性以及生化反应的滞后性。生化反应各个要素之间是一个相互依赖的整体,其间存在灵敏度与鲁棒性之间的矛盾,一旦失调，可靠性问题非常突出，如果条件改变有可能导致系统崩溃，控制系统工作瘫痪。

针对上述控制论特性，有必要探索更好的控制策略，以使污水处理过程处于期望的理想控制状态。

3　控制策略与控制算法

3.1控制策略

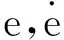
图6　基于知识的广义控制模型

针对生物污水处理过程的控制论特性，可供选择的控制策略虽然不少，但真正适用的并不多。比如，专家系统控制本质上是一种智能化的计算机程序系统,其特征信息的采集与表达技术难度大，尽管基于人类专家知识，在理论上可以处理相关领域的控制问题,但很难建立完备的知识库，受不确定性因素影响，该策略未必是好的选择，因为工程实现的技术难度太大。

模糊控制方法适用于对复杂过程和数学模型不精确过程的控制，但不确定性因素导致隶属函数选取难以确定，因此很难建立适合生物污水处理过程特性的模糊控制规则。该控制策略往往需要与其他方法配合使用，因此很难预料采用模糊控制及其改进方法可以获得好的控制效果。

神经网络控制可逼近任意的非线性特性，具有强大的学习能力和很好的容错性,并且可同时处理定量、定性数据以实现对过程的控制，但其预测能力主要取决于训练数据样本状况。由于受到不确定性因素影响，对污水处理过程很难获得足够的训练样本数据，即使能获得网络训练过程中所需要的样本数据，也有可能在训练过程中陷入局部极值。此外，对过程中存在的干扰和不确定性，神经网络控制则显得无能为力，因此该控制策略不可取。

仿人智能控制(HSIC)策略基于人类在进化过程中积累的智慧，其本身就是模拟人类的控制经验。HSIC在功能和结构方面有其显著的特征，可较好地兼顾各方面的控制品质要求[14]。比如：在控制过程中可对控制过程实施开环与闭环相结合的多模态控制；无需更多的过程先验知识与严格的数学模型就可实现优化控制；推理方式既可以采用启发式也可以应用直觉的推理逻辑等。总之，其显著特征就是模仿实际现场操作者的控制行为，按照实施控制后的过程偏差方向与偏差大小及其变化率方向与大小实施多模态的控制，因此所构造的控制算法更加贴近实际。实质上，生物污水处理过程控制就是要保证在DO浓度为2.0mg/L时使有机污染物获得最大程度地降解，可见其控制过程就是一个自动跟踪控制的过程。由于HSIC控制策略能兼顾鲁棒性与精确性、快速性与平滑性等技术性能要求，因此，仿人智能控制是一种值得一试的控制策略。

3.2控制算法

如图6所示：若e增大就应施加控制以抑制其增大；若e减小就应减小控制，并观察其变化趋势，同时记录其极大值，并将其作为下次控制校正的参考。按照自动控制原理，基于HSIC控制的原型算法可以概括为：

算法中： u为控制器输出; Kp，k，em,i分别为待定的比例系数、小于1的抑制系数和误差e的第i次峰值。

4　过程仿真及其结果分析

4.1过程仿真

以具有典型代表意义的二阶时滞模型为例，以PID控制为参照，若HSIC控制策略具有强鲁棒性，那么该控制策略就可取。设模型为

现基于Matlab对上述模型进行实验仿真。选取模型参数为：K = 1，τ = 2s，T1= 1.2s，T2= 2.0s。

如图6所示的广义控制模型，对同一过程分别采用PID和HSIC进行控制。在控制输入为单位阶跃时，图7中的曲线1和曲线2分别采用PID和HSIC控制的过程响应。为考察模型变化对过程响应的影响，现从原模型中去掉一个一阶环节1/(2s+1)，显然过程阶次与参数都有重大变化。相同条件下，图8中的曲线1和曲线2分别为PID和HSIC控制的过程响应。

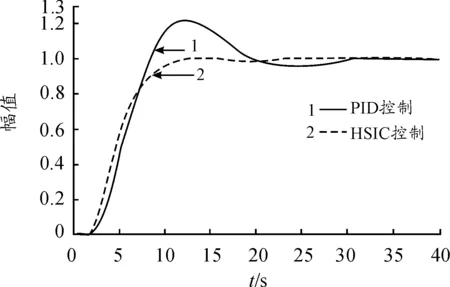
图7　二阶时滞模型的过程响应

图8　一阶时滞模型的过程响应

假设其过程模型为W(S)=e-10s/(s+1)(2s+1)，在上述条件下，在t=15s时加入脉冲宽度为0.2s、脉冲幅度为0.5的强脉冲干扰信号。图9中的曲线2和曲线1分别为PID和HSIC控制的过程响应。

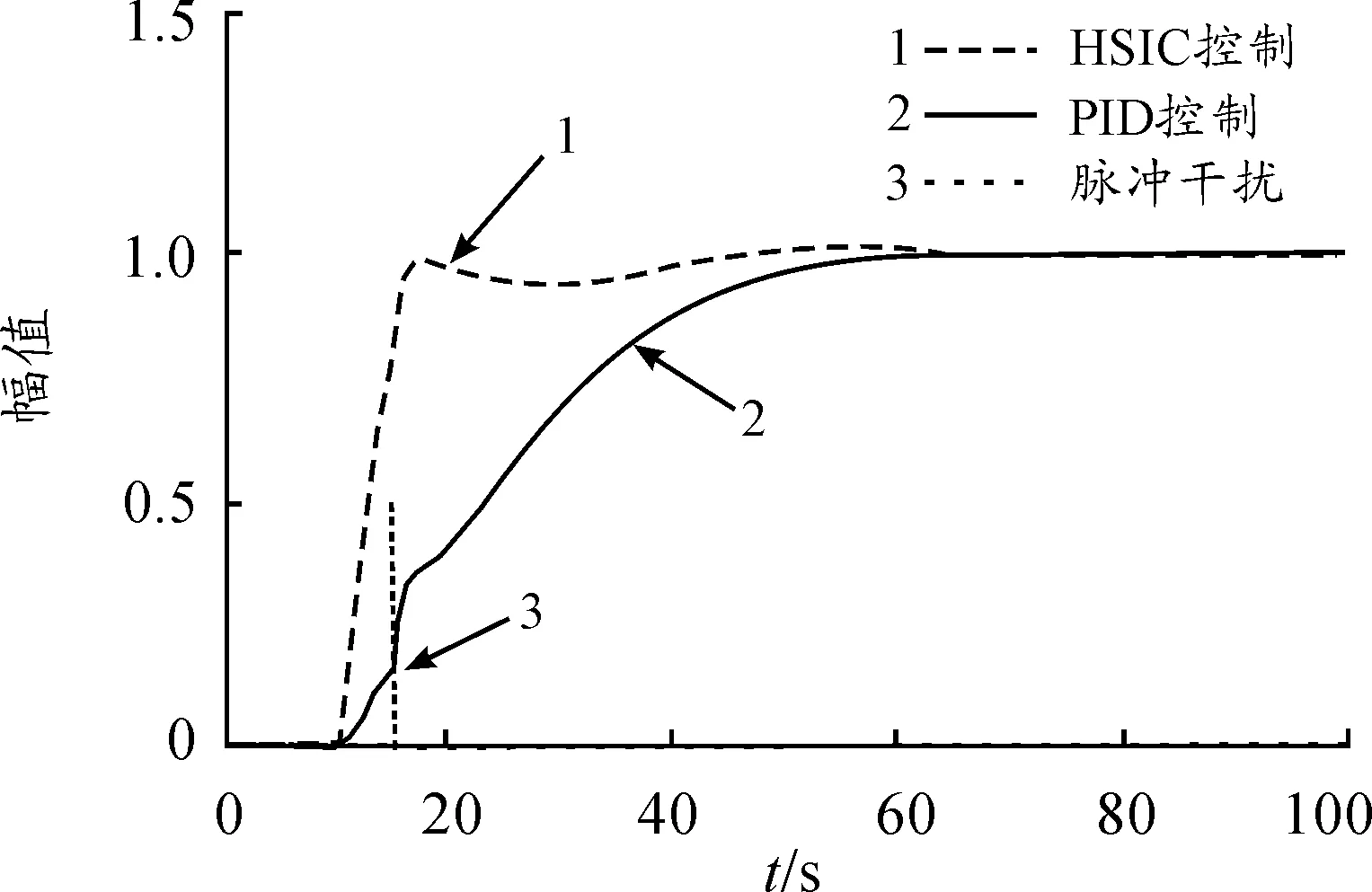
图9　强干扰下的过程响应

4.2仿真结果分析

由图7中曲线1和曲线2的对比可知：HSIC控制更加平稳，响应上升时间更快，调节时间更短，没有超调产生，而且稳态控制精度更高。图8表明：在模型阶次与与参数发生重大变化时，HSIC控制更加平稳，响应上升时间更快，调节时间更短，仍然没有超调产生。显然，HSIC控制品质更好。在模型参数变化与外部强脉冲信号干扰下，由图9可知：HSIC控制的稳态控制精度高，上升时间快，过程响应特性平稳，其调节时间短，其过程响应几乎不受其影响，而PID控制已失去控制能力。

以上从等效角度模拟了生活污水处理不确定性复杂过程的控制效果，验证了HSIC控制策略的强鲁棒控制性能，因此对生活污水处理过程采用HSIC控制策略是可取的。

5　结束语

生活污水处理是一个具有诸多不确定性的复杂过程，很难实施定量的精准控制。本文描述了基于生化反应过程的控制论特性，探讨了与其相匹配的智能控制策略。仿真实验验证了HSIC控制策略的强鲁棒性能与优秀控制品质，为生活污水处理过程控制提供了一种可供参考的控制策略。

参考文献：

[1]NIB,YUH.Mathematicalmodelingofaerobicgranularsludge—Areview[J].BiotechnologyAdvances，2010，28(6)：895-909.

[2]NUHOGLUA，KeskinlerB，YildizE.Mathematicalmodelingoftheactivatedsludgeprocess—theErzincancase[J].ProcessBiochemistry,2005，40(7)：2467-2473.

[3]DAVIDR.Modelingandnumericalsimulationofsecondarysettlers：AMethodofLinesstrategy[J].WaterResearch，2009，43(2)：319-330.

[4]王玥.城市生活污水处理过程控制与优化的研究[D].北京：北京化工大学，2012.

[5]夏静文.污水处理工艺设备系统模型研究与仿真[D].太原:太原科技大学,2008.

[6]蓝梅.缺氧—好氧活性污泥法数学模型研究[D].上海：同济大学,2005.

[7]王闯.活性污泥数学模型研究[D].上海：同济大学,2003.

[8]张玉环,张俊贞,李哲.SBR法基质降解数学模型的建立和参数估计[J].天津理工学院学报,2004,20(4):55-57.

[9]李卫红,关卫省.SBR法动力学初探[J].西北建筑工程学院学报(自然科学版),2000,17(2):76-79.

[10]BAKSHIBR，STEPHANOPOULOSG.Wave-Net:amulti-resolutionhierarchicalneuralnetworkwithlocalizedlearning[J].AIChEJournal,1993,39(1):57-81.

[11]乌尔松G,纽厄尔B.污水处理系统的建模、诊断和控制[M].北京：化学工业出版社,2004.

[12]彭莉，林鹰，杨奕.复杂系统控制中的相关技术讨论[J].西南师范大学学报，2004,29(6):1066-1068.

[13]王喜峰，贾仰文，牛存稳.基于水环境复杂系统理论的地下水氮污染负荷来源的测度方法[J].重庆理工大学学报(自然科学)，2015(1):47-52.

[14]李祖枢,涂亚庆.仿人智能控制[M].北京：国防工业出版社，2003.

(责任编辑刘舸)

收稿日期：2016-03-26

基金项目：重庆市教委科技项目(渝教科2013-4-02)

作者简介：邓新莉(1975—)，女，工程师，硕士，主要从事电子信息工程与检测系统设计方面的科研工作。

doi:10.3969/j.issn.1674-8425(z).2016.07.015

中图分类号：TP273

文献标识码：A

文章编号：1674-8425(2016)07-0086-07

StudyonBiologicalModelingandControlStrategyforSanitarySewageTreatmentofCity

DENGXin-li1,LIUShan2

(1.ChongqingRadio&TVUniversity,Chongqing400052,China;2.ChongqingHanjinTechnologyCo.,Ltd.,Chongqing400010,China)

Abstract:In order to overcome the sewage treatment being difficult to achieve optimal control caused by the influences such as being more in variables, uncertainties and other factors, the paper explored the biological modeling and control strategy of sanitary sewage treatment. It discussed the sewage biological treatment technics and the reaction mechanism, and constructed the dynamic model of biochemical reaction, and studied on cybernetics characteristics of the reaction process, and proposed the control strategy matching with the cybernetics characteristics of the reaction process. Experimental simulation has been verified that intelligent control strategy based on control of dissolved oxygen concentration can automatically tracked the desired state of the concentration of dissolved oxygen in sanitary sewage treatment. Research results show that the intelligent control can better achieve optimizing control of sanitary sewage treatment of city, and the proposed control strategy is feasible and effective.

Key words:activated sludge method; biological sewage treatment; dissolved oxygen control; optimizing control

引用格式：邓新莉，刘珊.城市生活污水处理的生物建模与控制策略研究[J].重庆理工大学学报(自然科学)，2016(7):86-92.

Citationformat：DENGXin-li,LIUShan.StudyonBiologicalModelingandControlStrategyforSanitarySewageTreatmentofCity[J].JournalofChongqingUniversityofTechnology(NaturalScience)，2016(7):86-92.