浅析导数在函数中的应用

琚金玲

（河南师范大学 河南新乡 453007）

浅析导数在函数中的应用

琚金玲

（河南师范大学 河南新乡 453007）

高中新修订的数学教学大纲中增加了导数的概念，导数的引入不仅增加了高中数学的深度，加强了在教学过程中由有限到无限的辨证思想的教育，也为以后数学分析等基础学科的研究奠定了坚实的基础，导数的意义深远，它可以与函数联系起来，也可以与物理方向联系起来，是微分学中最基本的概念，本文主要就导数在一元函数，多元函数方面的应用进行简单的探讨。

导数；一元函数；多元函数；应用

在数学学习中，导数作为解决数学问题不可缺少的工具，它的地位是毋庸置疑的。把导数真正运用到数学中去，使导数在一元函数，多元函数中的应用充分体现出来。

1 导数在一元函数中的应用

1.1 可导与连续的关系

定理1[1]如果在点x0处，函数f（x）是可导的，那么f在x0处是连续的。

注1[1]可导只是f（x）在该点连续的充分条件，而不是必要条件。例如函数f（x）=|x|在点x=0处是连续的，但是并不是可导函数。

例1设有函数 （fx），当x=0时，（fx）=0，当x≠0时，；那么若（fx）在x=0连续，m为何值？若（fx）在x=0可导，m为何值？

1.2 利用导数研究函数的根

研究函数的根，也就是要弄清楚它的图像与x轴的交点。这样的点有多少个，那么这个函数就有多少个根。利用导数，就可以判断函数根的问题。

例2若k＞0，试问k是何值时，arctanx-kx=0存在正实根？

解：作f（x）=arctanx-kx，k＞0，则有f′（x）=1/（1+x2）-k，f（0）=0。

如果方程arctanx-kx=0有正实根x0，由罗尔中值定理，存在ξ∈（0，x0），使f′（ξ）=0，即1/（1+ξ2）-k=0，k=1/（1+ξ2），则有0＜k＜1。反之，如果0＜k＜1，则 f′（0）=1-k＞0。于是故存在 h1＞0，使得，由此得f（h1）＞0。

综上可知，若 0＜k＜1，arctanx-kx=0 存在正实根。

1.3 利用导数研究函数图像

先确定f′（x）=0和f″（x）=0成立和f′（x），f″（x）不存在的点，利用这些点把f（x）的定义域分为若干个子区间，用列表显示出来，最后综合分析画出图像。

例3做出y=3x5-5x3的图像.

解：函数定义域是（-∞，+∞），若f（x）=3x5-5x3，那么：

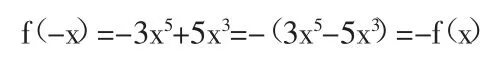
故f（x）是奇函数.若x，y分别为零，那么f（x）和x，y轴的交点是：

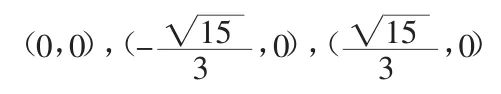
又 y′=15x4-15x2，令 y′=0，则 x=0，1，-1。又 y″=60x3-30x，令 y″=0，则有，那么有表1。

表1

做出函数图像为如图1。

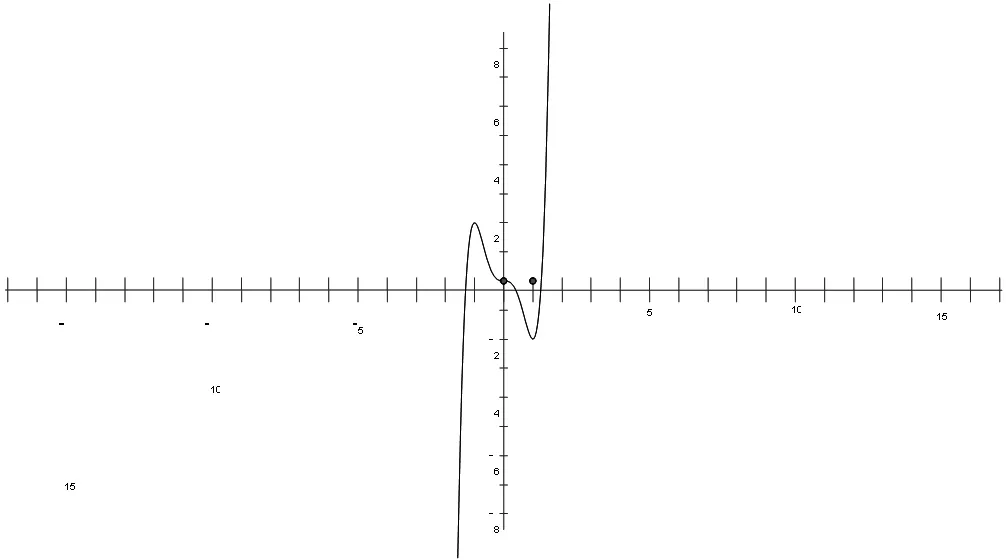
图1

1.4 对复合函数求导方法

定理2[2]如果u=φ（x）在x0是可导的，y=f（u）在u0=φ（x0）是可导的，那么复合函数 f·φ 在 x0可导，并有 （f·φ）′（x0）=f′（u0）φ′（x0）=f′（φ（x0））φ′（x0）。

注2我们把上面的公式称作复合函数的求导公式，也称作链式法则，函数y=f（u），u=φ（x）的复合函数在点x的求导公式也可写作为

解：首先对上面的函数式取对数，那么有：

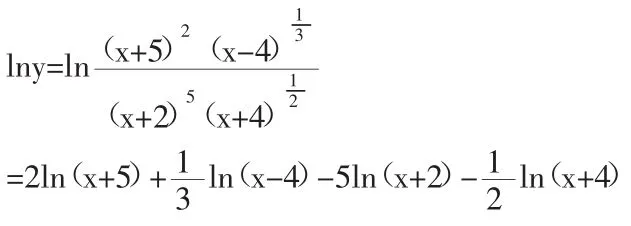
然后对上面式子两边分别求导，可以得到：

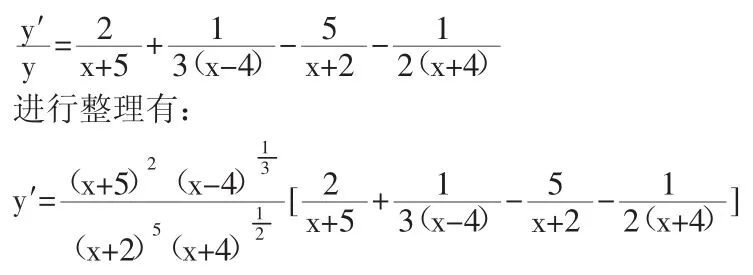
对复合函数求导可以用链式法则，但在某些情况下，函数会比较复杂，除了利用一些基本的求导法则，我们还有其他更为简便的方法.例如上面的例子如果我们用常规方法来做会比较麻烦，但我们用对数求导法使计算变的相当简便。

1.5 导数在参变量函数中的应用

利用导数可以更简便的解决参变量函数问题，通过研究下面这个例题，能够加强对数学知识的理解：

解：假设 t=t0，那么相对应的点是（x0，y0），于是：

2 导数在多元函数中的应用

与一元函数类似，在多元函数中，依旧可以得出两个极限表示式：

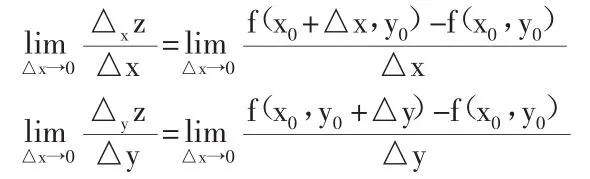
由第一个式子我们看出式子右边的极限是关于x的一元函数f（x，y0）在x=x0处的导数，第二个式子是关于y的一元函数f（x0，y）在y=y0处的导数。

2.1 偏导与连续的关系

在一元函数中，如果一个函数可导，那么这个函数必连续；而在二元函数中，如果偏导函数存在，那么这个函数不一定连续。具体看下面的这个例子：

2.2 偏导数与物理结合应用

偏导数不仅在数学中应用广泛，它也可以与物理等学科结合，解决科学中的实际问题.但是最重要的还是要掌握偏导数的求法，偏导数的求导方法是在最基本的求导法则基础上建立起来的[3]：

2.3 方向导数的应用

在很多数学问题中，我们不仅需要判断函数在两轴上的变化率，还要进一步研究函数在其他方向上的变化率，这就用到了方向导数。

例9设f（x，y，z）=x+y2+z3，确定f在P0（1，1，1）沿着方向l：（2，-2，1）的方向导数。

解：由题意 fx（x，y，z）=1，fy（x，y，z）=2y，fz（x，y，z）=3z2，则在点 P0（1，1，1）处有：

在数学教材知识中，导数起到了极其重要的作用，是处理数学问题的非常有效的工具。在上面的研究中，我们讨论了导数在一元函数，二元函数方面的应用，都起着化繁为简的作用。不仅是一元函数，二元函数，在隐函数的问题上，例如隐函数或隐函数组是否存在的判定，极值的确定等，都要以导数的知识为基础。

[1]华东师范大学数学系.数学分析（上册，第三版）[M].北京：高等教育出版社，2001：92～94.

[2]华东师范大学数学系.数学分析（下册，第三版）[M].北京：高等教育出版社，2001：116～134.

[3]郑永春.Jacobians法对热力学偏导数的应用[J].大理学院学报，2001，4（2）：91～94.

O172.1

A

1004-7344（2016）10-0030-02

2016-3-15

琚金玲（1992-），女，汉族，河南济源人，硕士研究生，研究方向为学科教学（数学）。