三相双降压逆变器中电感的磁集成方式比较与优化设计
吕林娜 肖 岚 祁 琦(南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京 210016)
三相双降压逆变器中电感的磁集成方式比较与优化设计
吕林娜肖岚祁琦
(南京航空航天大学江苏省新能源发电与电能变换重点实验室南京210016)
三相双降压逆变器克服了传统桥式逆变器中桥臂功率管直通的问题,可靠性高,但输出滤波电感数量多、体积大,利用磁集成的技术可以减小磁性元件的体积重量,提高系统功率密度。针对该问题从电感耦合方式的角度入手分析不同磁集成方案,从电路原理上讨论各方案的可行性及电感对进网电流波形和电路运行特性的影响。据此提出一种同名端相连不完全耦合的电感集成方案,其等效的三电感形式和传统双降压拓扑中两电感在电路中工作特性一致。和已有的磁集成方案及不采用任何磁集成方案相比,该方案在电感体积和滤波效果等方面均得到优化。最后设计并搭建一台15 kV·A的三相双降压并网逆变器原理样机进行实验验证,实验结果与理论分析吻合。
磁集成双降压三相逆变器耦合电感
0 引言
并网逆变器作为分布式发电系统与电网接口设备,起着至关重要的作用。三相双降压逆变器[1-4]克服了传统桥式逆变器桥臂功率管直通的问题,可靠性高,但磁性元件数量多,因此其滤波电感的磁集成技术的研究对提高系统功率密度具有重要意义。
并网逆变器中常用的滤波器有单L和LCL滤波器,其中LCL滤波器因具有体积小、高频谐波抑制能力强的优点而得到广泛应用。三相桥式逆变器中的LCL滤波器[5-9]共有六个滤波电感,每相在逆变器侧和网侧均有一个电感;而双降压逆变器每相有两个逆变器侧桥臂输出电感和一个网侧电感,如图1所示。
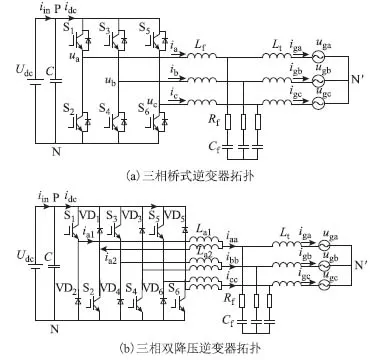
图1 三相桥式逆变器和三相双降压逆变器拓扑Fig.1 Topologies of three-phase bridge inverter and three-phase dual-buck inverter
网侧电感上高频电流纹波小,对应铁损小,可将网侧电感集成在网侧隔离变压器中。对逆变器侧两个桥臂输出电感,文献[10]将桥臂输出侧的两个电感异名端相连完全耦合实现磁集成,但该方案存在滤波电感失效的情况,此时电感等效阻抗为零,对进网电流的波形质量造成较大影响(在2.1节中详细分析)。文献[11]提出一种两磁心四绕组的方案,虽然每相桥臂仍有两个磁心,但每个磁心大小和不采用磁集成技术相比,磁心体积减小。文献[12]在单相双降压半桥逆变器中采用三电感的形式替代两电感,桥臂中串联两个防直通电感,桥臂中点级联LC滤波器。在级联双降压逆变拓扑[13,14]和三相双降压逆变拓扑[15]中也有三电感形式,电路工作原理和传统双降压逆变器一致。
三电感形式的双降压拓扑中将双降压桥臂中防直通电感与滤波电感分离,电感总体积重量有一定减小,但电感数量需进一步优化。以一相桥臂为例,分析了桥臂输出电感完全耦合集成和不完全耦合集成时的几种情况(同名端相连、异名端相连及混合型连接等),得到每种集成方式下的对应等效电路及其工作模态。以滤波电感的滤波效果为准则,分析了不同磁集成方案的可行性。通过对比集成前后磁件体积及逆变器侧滤波电感值,提出一种优化的磁集成设计方案——同名端相连不完全耦合集成。最后通过一台15 kV·A的三相双降压并网逆变器原理样机进行了实验验证。
1 双降压逆变器的工作原理
三相双降压逆变器有全周期和半周期两种工作模式,以a相桥臂为例,分析两种工作模式下工作情况。a相电路拓扑如图2a所示,其中 S1、S2为开关管,VD1、VD2为二极管,La1、La2为逆变器侧桥臂输出电感,假设La1=La2=Lf。
1.1全周期工作模式
电路工作在全周期工作模式时,开关管S1、S2高频互补工作。a相电流波形如图2b所示,其中iaa为a相桥臂输出电流,ia1和ia2分别为流过电感La1和La2的电流,其参考方向如图2a所示,则

令

式中,ω为输出角频率。
此时一个周期内可划分为4种工作模态:
模态1:S1开通,S2关断,iaa为正时,电流ia1从直流侧P点经S1、La1流向交流侧;同时由于流过La2的电流不能突变,因此VD1续流导通,电流ia2从交流侧经La2、VD1流向直流侧。
模态2:S1关断,S2开通,iaa为正时,由于流过La1的电流不能突变,因此在S1关断瞬间VD2续流导通,电流ia1从直流侧N点经VD2、La1流向交流侧;电流ia2从交流侧经La2、S2流向直流侧。
模态3:S1开通,S2关断,iaa为负时,与模态1类似。
模态4:S1关断,S2开通,iaa为负时,与模态2类似。
在全周期工作模式下,a相桥臂输出电流iaa基波为正弦波,而桥臂串联电感电流ia1和ia2则为直流分量叠加正弦分量。无论是在哪种模态下,每相的两个桥臂串联电感均为并联工作,等效滤波电感的大小为0.5Lf。
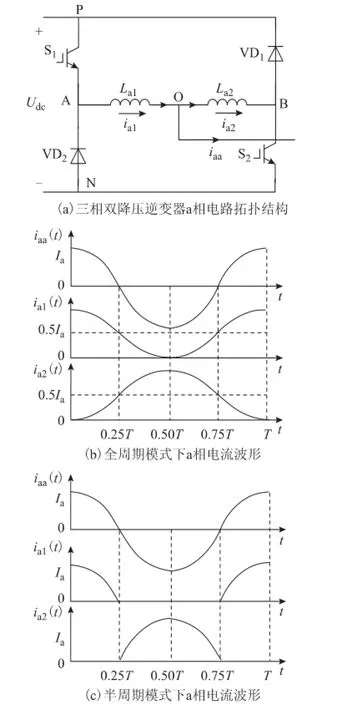
图2 a相电路拓扑和a相电流波形Fig.2 A-phase circuit topology and a-phase current waveforms
1.2半周期工作模式
半周期工作模式下,三相双降压逆变器的每相桥臂两个开关管分别在半个周期内高频工作,另外半个周期内关断。此时该相相电流波形、逆变器侧桥臂输出电感电流波形如图2c所示,一个周期内也可划分为4种工作模态:
模态1:S1开通,S2关断,iaa为正时,电流ia1从直流侧P点经S1、La1流向交流侧。因为图1b中所示的直流侧中点N和交流侧中点N'存在电位差,在逆变状态可能出现A点电位高于P点电位或低于N点电位的情况[16],此时VD1被迫导通,电流ia2流过La2,La1和La2并联工作。当A点电位低于P点电位时,没有电流流过La2,iaa=ia1。
模态2:S1关断,S2关断,iaa为正时,由于流过La1的电流不能突变,在 S1关断瞬间VD2续流导通,电流ia1从直流侧N点经VD2、La1流向交流侧;当A点电位低于 P点电位时,没有电流流过电感 La2,iaa=ia1;当A点电位高于P点电位时,VD1被迫导通,电流ia2流过La2,La1和La2并联工作。
模态3:S1关断,S2开通,iaa为负时,和模态1类似。
模态4:S1关断,S2关断,iaa为负时,和模态2类似。
在半周期工作模式下,a相桥臂输出电流iaa基波为正弦波,而两个桥臂串联电感的电流ia1和ia2则为正弦半波。在A点电位低于P点电位或高于N点电位时,两个桥臂串联电感只有一个流过电流,等效滤波电感大小为Lf;在A点电位高于P点电位或低于N点电位时,等效滤波电感大小为0.5Lf。
2 桥臂输出电感完全耦合
2.1异名端相连
以a相电路为例,异名端相连完全耦合的电路如图3所示,两个耦合电感的自感La1=La2=Lf,互感M=Lf。以图中电压电流方向为参考方向,有uAO=uOB恒成立。
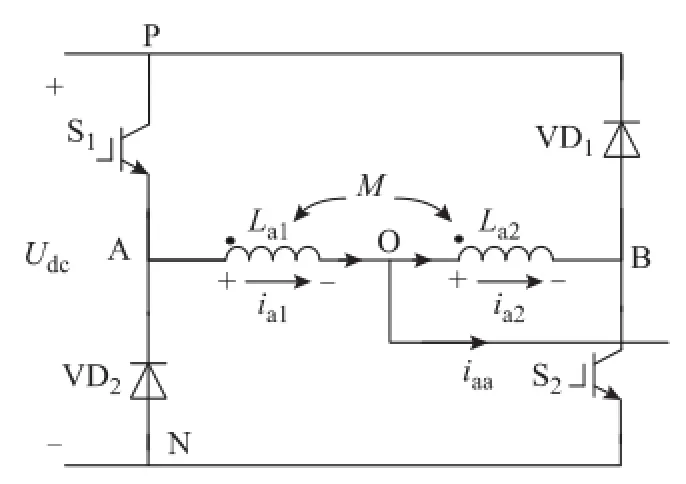
图3 异名端相连电感完全耦合的a相电路拓扑Fig.3 A-phase circuit utilizing complete-coupled inductors with non-dotted terminals connected
全周期工作模式下,当S1开通时,VD1续流导通;S2开通时,VD2续流导通。因此,无论是在S1、VD1导通还是S2、VD2导通时,uAB=0恒成立。所以
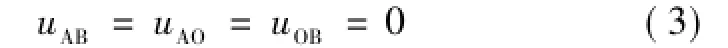
此时电感La1、La2上电压恒为零,耦合电感在电路中等效阻抗为零,对各次谐波均未起到滤波效果,LCL滤波器退化后桥臂输出脉冲电压直接接到电容,会产生很大脉冲电流。
半周期工作模式下的三相双降压逆变器在A点电位高于P点电位或低于N点电位时,La1和La2并联工作,同全周期工作模式,耦合电感对各次谐波均未起到滤波效果,此时滤波效果变差。
2.2同名端相连
仍以a相电路为例,同名端相连完全耦合的电路如图4a所示,两个耦合电感的自感La1=La2=Lf,互感M=Lf。以图中电压电流方向为参考方向,有uAO= uBO,A点和B点等电位。从耦合电感等效的角度分析,图4a所示耦合电感可等效为图4b形式。将等效后的电感带入图4a,可得采用同名端相连完全耦合的方式集成桥臂输出侧两个电感的等效电路图。此时,双降压电路可等效为桥式电路,不论全周期工作模式或半周期工作模式均有等效滤波电感M=Lf,与未集成时全周期模式和半周期模式时电感La1和La2并联时相比滤波效果变好。不过电路失去双降压电路桥臂防直通的特性。
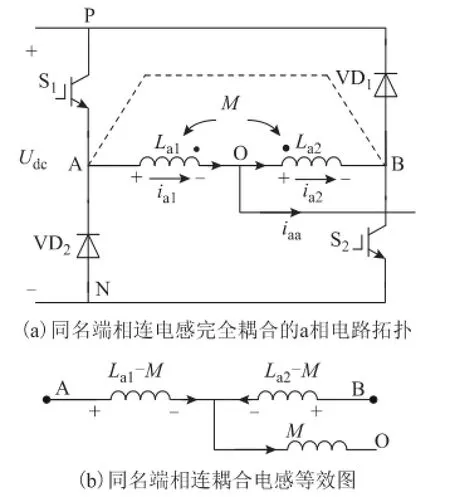
图4 同名端相连电感完全耦合时的电路Fig.4 Circuit utilizing complete-coupled inductors with dotted terminals connected
2.3混合型连接——两磁心四绕组
以a相电路为例,两磁心四绕组的耦合方式如图5a所示,其中两个耦合电感分别为T1、T2,T1上有两个绕组自感为 LA1、LA2,T2上两个绕组自感为LB1、LB2,有LA1=LA2=LB1=LB2=0.5Lf,耦合绕组间的互感也为0.5Lf,同名端连接方式如图5a所示。
以图中电流方向为参考方向,有uCO=uDO,C点和D点同电位,根据图4b的等效电路,耦合电感T2可等效为图5b的形式。根据图5c所示的异名端相连耦合电感等效图,化简得到图5d的等效图。从图中可看出,两磁心四绕组耦合方式下等效电路与未集成时电路相同,既不会出现异名端相连时滤波电感失效的情况,也不会有同名端相连时退化为传统桥式的问题。
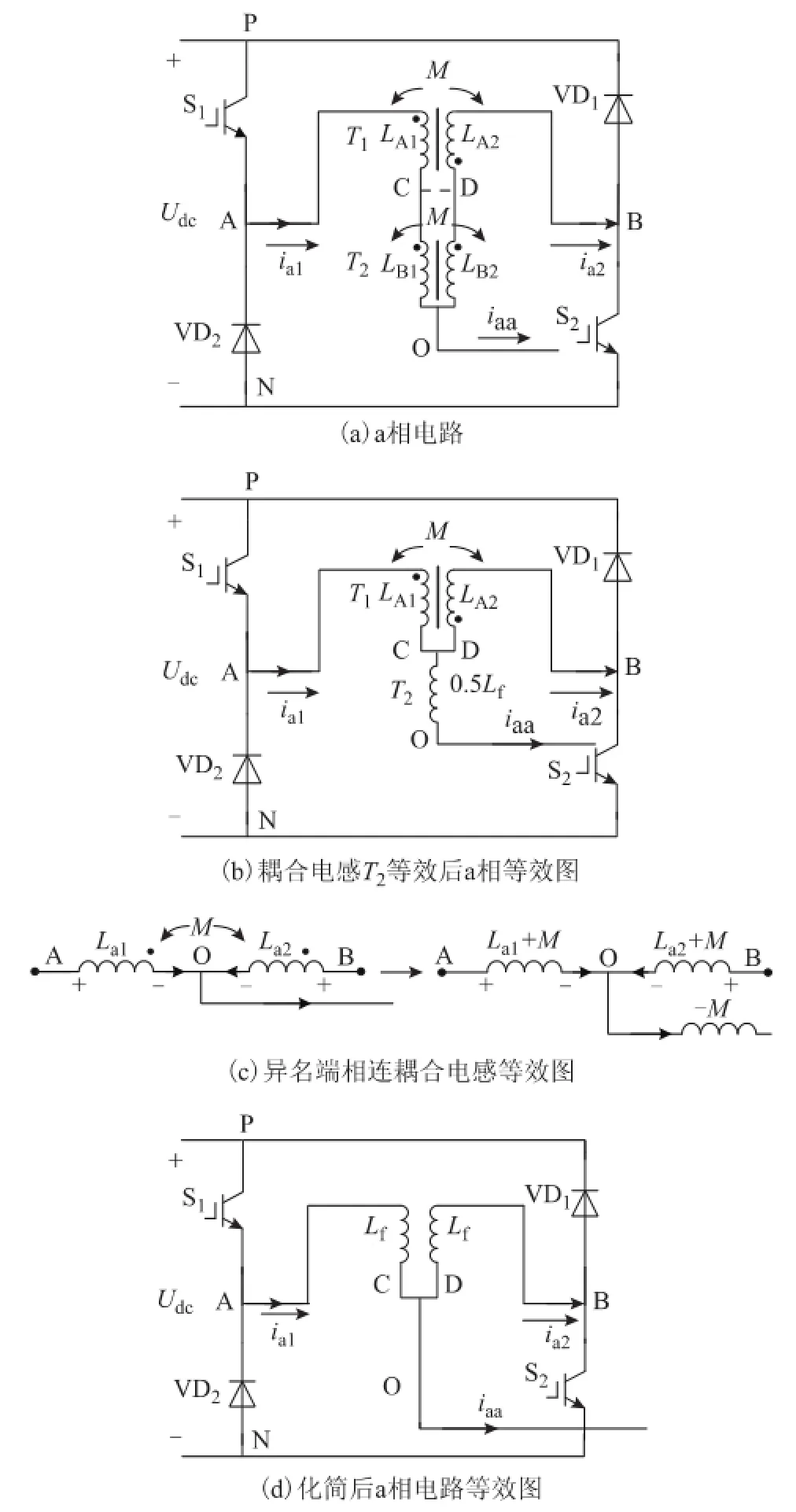
图5 两磁心四绕组电感完全耦合时的电路Fig.5 Circuit with coupled inductors integrated in two magnetics with four windings
3 桥臂输出电感不完全耦合
3.1同名端相连
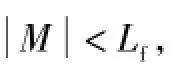
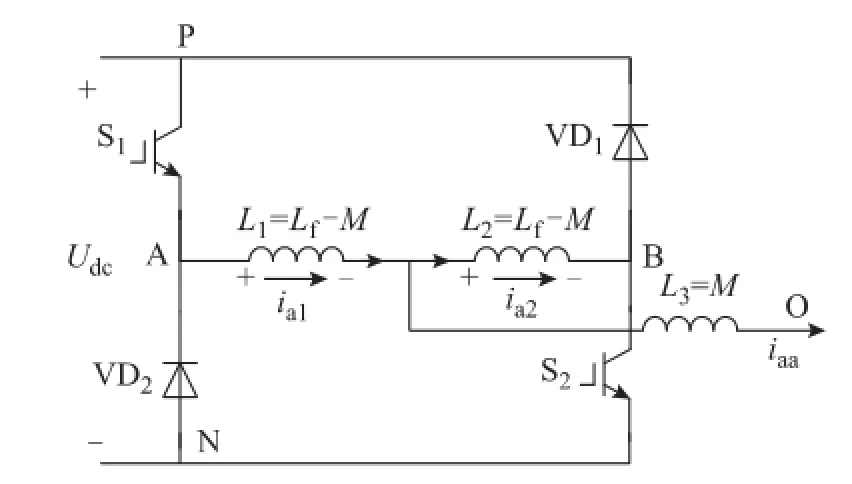
图6 电感不完全耦合集成时a相等效电路Fig.6 Equivalent circuit of a-phase with uncomplete-coupled inductors
该等效电路桥臂输出侧等效出3个电感
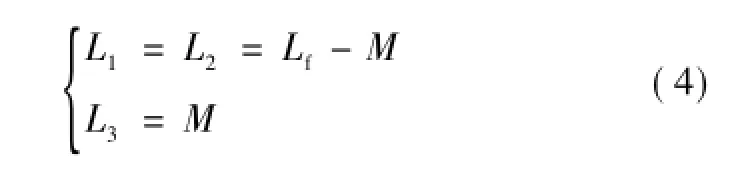
由于电感L1、L2的存在,只要L1、L2足够大,在S1、S2开关瞬间,变换器不存在桥臂直通的问题,有效避免了电感完全耦合时桥臂中点等电位的情况。而图中的三电感割集结构,在全周期工作模式下,因为桥臂中点A、B等电位,电感L1与L2并联后与L3串联,可等效为一个电感
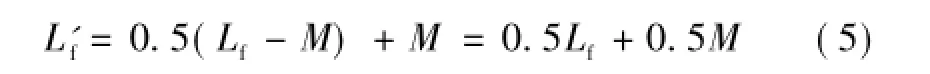
在半周期工作模式下,根据第1节的分析,在A点电位低于P点电位或高于N点电位时,电感L1或L2与L3串联,可等效为一个电感
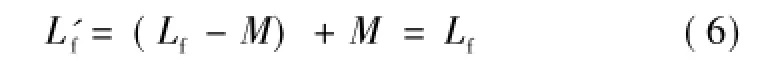
在A点电位高于P点或低于N点时,L1与L2并联后与L3串联,可等效为一个电感,同全周期工作时。由上述分析可知,逆变器侧桥臂输出电感不完全耦合集成时,该等效电路从工作原理上与三相双降压电路完全一致。
此时也对应有同名端相连与异名端相连两种情况,根据式(6)可知,只有一个电感工作时,两种连接方式下的等效滤波电感都是Lf,与电感不集成时的等效滤波电感相同;根据式(5)可知,全周期工作模式时或半周期工作模式下电感La1和La2并联时,同名端相连时的等效电感大于不集成时,而异名端相连时的等效电感小于不集成时。全周期工作模式和半周期工作模式下都存在电感La1和La2并联的情况,因此采用等效滤波电感值增大的逆变器侧桥臂输出电感同名端相连不完全耦合集成方案。
3.2耦合结构及设计原则
若电感La1和La2分别绕制,且均采用三柱非晶磁心,结构示意图如图7a所示。La1和 La2电感值相等,且流过电流有效值及峰值也相等,因此两电感磁心结构相同。根据磁路的对称性,电感表达式为

式中,L为电感值,H;N为绕组匝数;Φ为绕组匝链磁通,Wb;i为流过绕组电流,A。采用同名端相连不完全耦合集成方案的耦合电感,可按照图7b所示的结构,将La1和La2集成在四柱非晶磁心上。磁心可分为Ⅰ、Ⅱ、Ⅲ三部分,磁心Ⅰ中为公共耦合磁通,磁心Ⅱ和Ⅲ对称,为单独磁化磁通路径。La1和La2的自感L及互感M表达式为
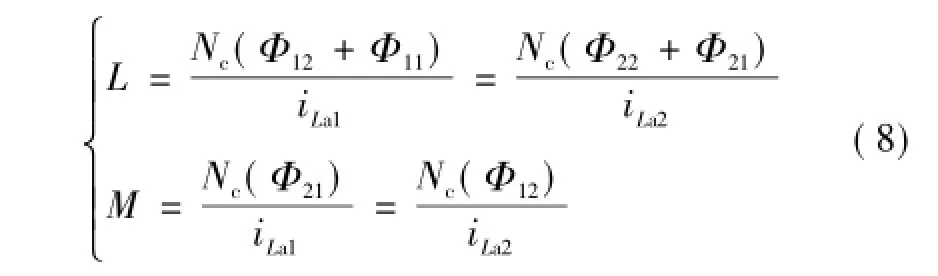
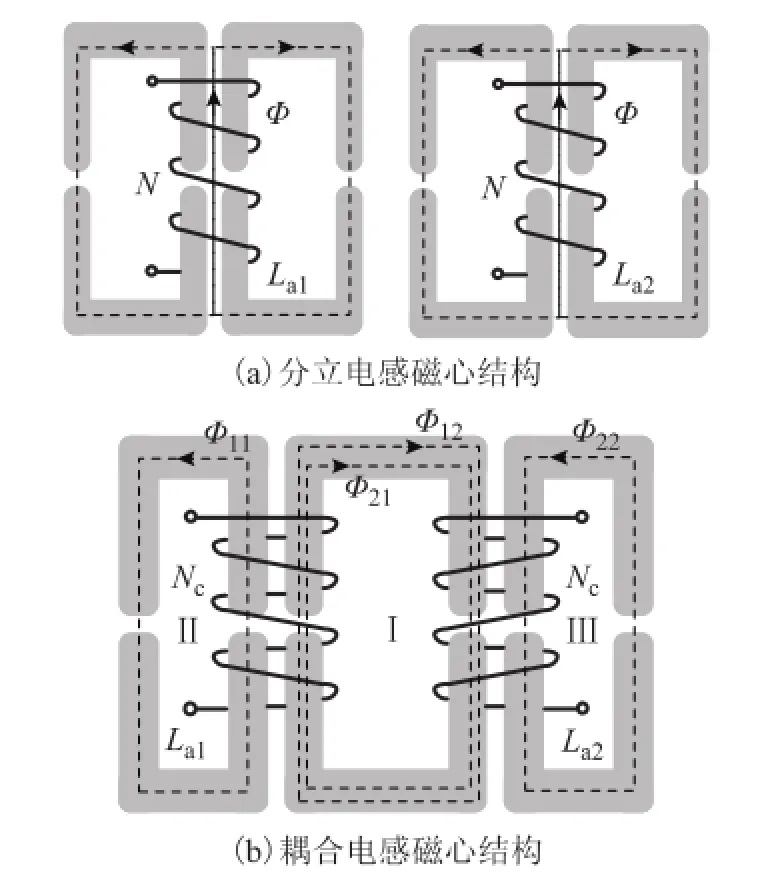
图7 电感结构示意图Fig.7 Structure diagram of inductor
若两磁柱最大工作磁通密度相同,即工作磁通和柱截面积呈正比关系,根据式(8)可得柱截面积间关系为

式中,SI、SII分别为磁心柱Ⅰ、Ⅱ的截面积。根据式(7)和式(8)中自感表达式及最大磁通密度相同假设,可知分立电感和耦合电感绕组匝数及等效柱截面积乘积相同
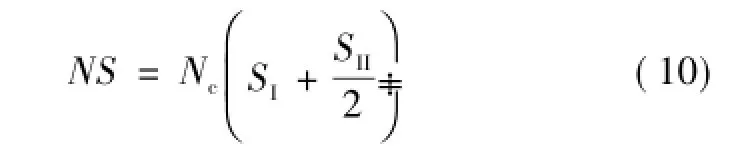
式中,S为图7a中所示柱截面积。
将式(9)带入式(10),化简后可得
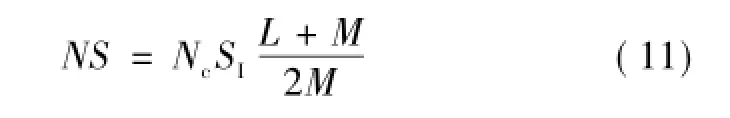
根据式(11)可选择不同的耦合电感的磁心结构参数,设计时选择分立电感和耦合电感绕组匝数相同,耦合电感的磁心尺寸可由式(9)和式(11)及对应分立电感尺寸得到。
选择分立电感和耦合电感绕组匝数相同时,根据式(11)和图7可知耦合电感和分立电感的磁心窗口面积及绕组匝数相同。分立电感和耦合电感的总柱截面积分别为

由式(12)可知采用同名端相连不完全耦合集成方案的耦合电感的磁心体积和分立电感相比得到优化,且和耦合系数相关。耦合系数越大(互感M越大),体积优化越明显。
4 电感集成方式比较
通过前述分析可知,采用同名端相连不完全耦合的磁集成方案和两磁心四绕组的磁集成方案都能很好地实现电路功能,下面对这两种磁集成方案的磁件大小和逆变器侧滤波电感值做进一步分析,并进行比较[17]。
4.1磁件大小
首先做如下假设:
1)电感选用相同的磁心材料和导线材料。
2)电路输入输出参数和功率相同。
3)电路桥臂输出的等效调制波形相同,含有相同的谐波含量。
将使用相关电气参数间接对3种情况下磁件的体积进行比较。由电感设计原理和相关文献可知,磁心的最大工作磁动势Fmax间接决定了磁心的大小[18],在相同条件下,Fmax越大,磁心越大;反之亦然。因此,可通过比较3种情况下桥臂输出侧电感磁心的最大工作磁动势来比较电感磁心的大小。
主要分析半周期工作模式下的情况,全周期工作模式类似。以下讨论都基于半周期模式。
假设逆变器进网相电流的最大值为Imax,不集成的双降压逆变器每相两个桥臂串联电感的绕组匝数均为N,电感值
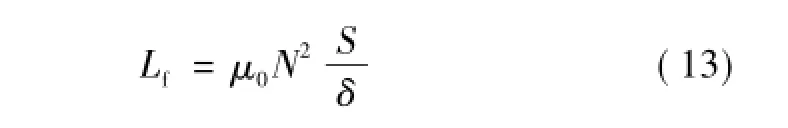
式中,μ0为真空磁导率;S为磁心截面积;N为绕组匝数;δ为气隙大小。此时,单个电感最大磁动势为Fmax1=NImax,两个电感的最大磁动势和为2 NImax。
绕线的截面积正比于流过电流的有效值,假如选取相同的电流密度,则绕组体积与绕组安匝呈正比,对比绕组体积可通过比较绕组安匝来间接表征。流过每个桥臂输出侧电感的电流有效值Irms为输出相电流有效值的0.707倍,即最大值的0.5倍:Irms=0.5 Imax。
对于同名端相连不完全耦合磁集成的双降压逆变器,绕在同一个磁心上的两个耦合的绕组本身的自感大小为La1=La2=Lf。如果选择S、δ均相同的磁心,由式(13)可知,每个耦合绕组的匝数也为N。当电路工作在相电流为正和负的半个周期时,电流分别从耦合电感的同名端流出和流入,最大工作磁动势为Fmax2= NImax。可见同名端相连不完全耦合磁集成方案与无集成方案下电感最大工作磁动势相同,但其只需一个磁心,磁件减小。
对于两磁心四绕组方式磁集成的双降压逆变器,4个绕组的自感大小为LA1=LA2=LB1=LB2=0.5Lf,相同磁心的条件下,每个绕组为无集成方案时单个电感绕组匝数的0.707倍,即0.707 N。以耦合电感T2为例分析单个磁件的最大磁动势,当电路工作在相电流为正的半个周期时,电流从绕组LB1的同名端流入,此时LB2没有电流流过;负半周类似。因此T1、T2的最大工作磁动势为Fmax3=NImax。可见两磁心四绕组耦合方案下,每个磁心的大小仅为不集成时单个电感磁心的0.707倍。磁心体积的减小会造成单个绕组匝数和气隙大小的改变,将电感的表达式做如下变换可得
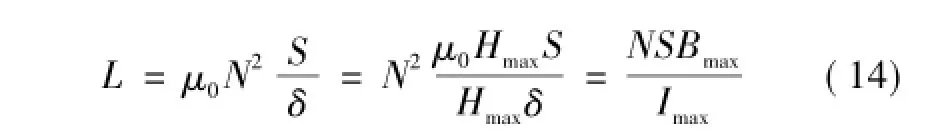
式中,Hmax为磁场强度最大值,Hmaxδ=NImax。根据B-H曲线,μ0Hmax=Bmax。相同条件下,不同集成方案的Bmax相等,Imax也相同。则根据上述假设,两磁心四绕组集成方案下每个绕组匝数为不集成方案下的0.707倍,磁心小于不集成方案。
对于某一相的逆变器侧桥臂串联电感来说,不集成的三相双降压逆变器、采用同名端相连不完全耦合集成的三相双降压逆变器和采用两磁心四绕组方式集成的三相双降压逆变器的磁件整体大小对比如表1所示。通过比较磁件磁心的最大磁动势之和表征总磁心的大小,通过比较绕组安匝之和表征绕组的大小。由表1可知,同名端相连不完全耦合和两磁心四绕组耦合的方案相比,磁件体积的减小更明显,且不会造成绕组安匝更大等负面效果,是一种较好的磁集成方案。
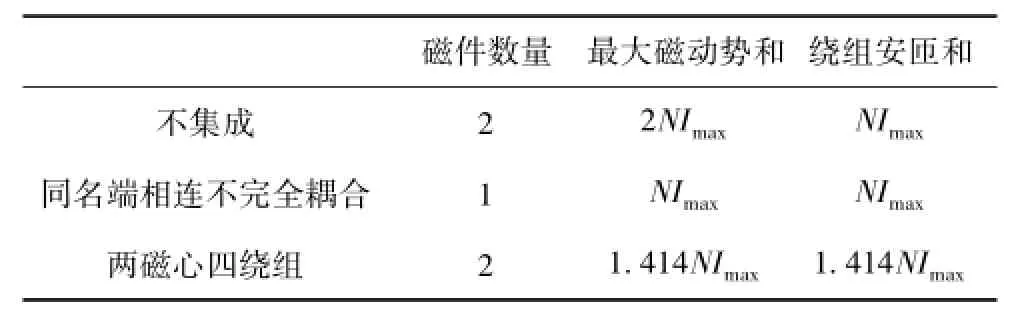
表1 不同磁集成方式下电感整体大小比较Tab.1 Total size comparison between different integration
对于全周期工作模式,电感在整个周期内都有电流流过,且流过每个电感的有效值比半周期大。但由于3种情况下电流有效值仍相同,所以不影响比较结果。因此,对于全周期工作模式下,仍是采用同名端相连不完全耦合的磁集成方案较好。由此得到了一种在全周期工作模式和半周期工作模式下都具有优化性能的电感集成方案。
4.2等效滤波电感
第3节分析了不同磁集成方案的双降压电路工作在全/半周期模式下的等效滤波电感值,如表2所示。从表中可看出,两磁心四绕组集成的双降压电路的逆变器侧等效滤波电感和不集成的双降压电路的逆变器侧等效滤波电感相同。而同名端相连不完全耦合集成的双降压电路在全周期工作模式下的逆变器侧等效滤波电感为0.5Lf+0.5M,随着M的增大,等效滤波电感的大小增加,但M越大,桥臂中的串联电感越小,其防直通短路的特性越不明显,当M=Lf时,双降压电路退化为传统桥式电路,不具备桥臂防直通的特性;半周期工作模式下的逆变器侧等效滤波电感在电感单独工作时为 Lf,在并联工作时为0.5Lf+ 0.5M,和全周期相同。不论在哪种工作模式下,同名端相连不完全耦合集成的双降压电路的逆变器侧等效滤波电感值都比不集成的双降压电路大。在设计LCL滤波器时,考虑相同滤波效果时应取逆变器侧等效滤波电感值相同,采用同名端相连不完全耦合的集成方案时,可减小耦合电感值,从而减小滤波器的体积。

表2 等效滤波电感比较Tab.2 Equivalent inductor comparison
5 实验验证
为验证理论分析,搭建了一台15 kV·A的三相双降压逆变器原理样机。直流侧输入电压700 V,交流侧接三相220 V/380 V/50 Hz电网,开关频率为5 kHz,功率管为IGBT模块FF75R12RT4,滤波电容20 μF。网侧滤波电感0.4 mH;逆变器侧滤波电感采用非晶磁心,分立电感绕制在三柱磁心,耦合电感绕制在四柱磁心(如图7所示)。分立电感(左)和耦合电感(右)实物图如图8所示,分立电感尺寸为13.6 cm×9.6 cm× 7.4 cm,耦合电感尺寸为15.2 cm×10.6 cm×10.4 cm,采用所提出的耦合方法集成电感后尺寸减少约14%。和图7中对应,分立电感电感值L=2.3 mH;耦合电感自感La1=La2=2.3 mH,互感M=0.5 mH。

图8 电感实物图Fig.8 Photos of the inductors
在全周期工作模式和半周期工作方式下,对逆变器侧桥臂输出电感集成的情况分别进行实验。图9、图10分别为采用集成电感时三相双降压逆变器在全周期模式和半周期模式下的满载实验结果。图中uga为a相电压,iga、igb、igc分别为三相进网电流,dS1、dS2分别为开关管S1、S2驱动电压。
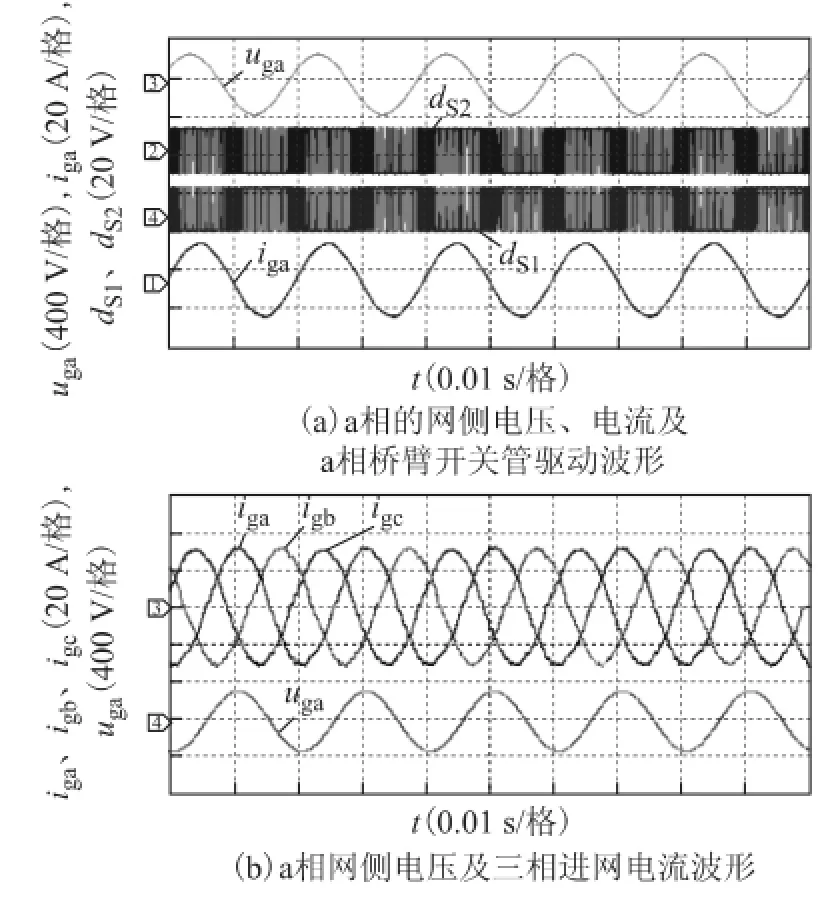
图9 电感集成时全周期工作模式下实验结果Fig.9 Experiment results of circuit with integrated inductors in full-cycle control method
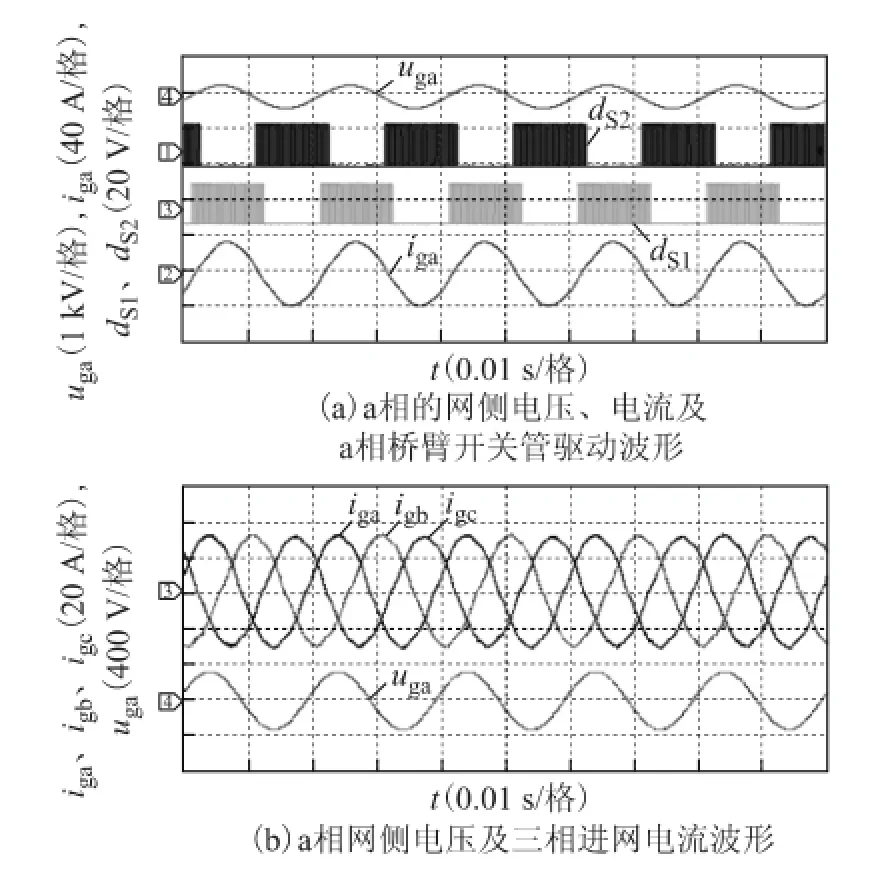
图10 电感集成时半周期工作模式下实验结果Fig.10 Experiment results of circuit with integrated inductors in half-cycle control method
图11为三相双降压逆变器工作在满载条件时,分别采用耦合电感与分立电感的a相电流谐波分布及THD比较。图11a为全周期模式下的频谱,采用分立电感和耦合电感THD分别为4.4%和4.0%。图11b为半周期模式下的频谱,采用分立电感和耦合电感THD分别为4.9%和4.8%。电路工作在全周期模式下时,集成后等效滤波电感值变大,滤波效果变好,进网电流THD减小;电路工作在半周期模式下时,因为电感并联工作的时间较短(仅在桥臂中点电位高于正直流母线/低于负直流母线时),因此进网电流的THD和全周期相比改善不明显。实验结果和理论分析一致。
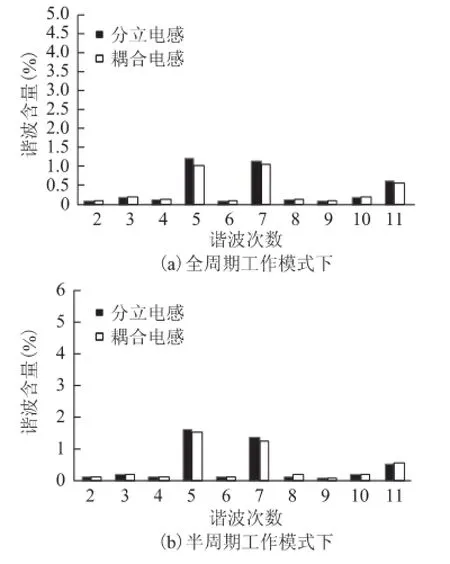
图11 电感集成前后a相电流谐波分布及THD比较Fig.11 Comparison of a-phase current harmonics and THD with discrete and coupled inductors
6 结论
本文主要对三相双降压逆变器桥臂侧输出电感磁集成技术进行了研究,讨论了全周期和半周期工作模式下电感完全耦合集成和不完全耦合集成时双降压拓扑的等效电路及集成电感的滤波效果,与电感不集成时的电路相比较,判别各集成方案的可行性。结合电感不集成时电路的性能参数,比较了两磁心四绕组集成和同名端不完全耦合集成两种磁集成方案的磁件体积大小及逆变器侧等效滤波电感值,并得出优化的集成方案——同名端相连不完全耦合电感集成,给出了具体的耦合结构设计及对应实验验证。该方案可有效减小电感尺寸,从而提高系统的功率密度;且和电感不集成时电路相比,进网电流THD减小。
[1]姚志垒,肖岚,魏星.双降压全桥并网逆变器[J].电工技术学报,2011,31(12):29-33.
Yao Zhilei,Xiao Lan,Wei Xing.A dual-buck fullbridge grid-connected inverter[J].Transactions of China Electrotechnical Society,2011,31(12):29-33.
[2]SunPengwei,LiuChuang.Three-phasedual-buck inverter with unified pulsewidth modulation[J].IEEE TransactionsonPowerElectronics,2012,27(3): 1159-1167.
[3]王赞,肖岚,姚志垒,等.双Buck电压源逆变器的半周期电流调制方法[J].电工技术学报,2007,22 (5):104-110.
Wang Zan,Xiao Lan,Yao Zhilei,et al.Half cycle current modulation method for dual buck voltage source inverter[J].TransactionsofChinaElectrotechnical Society,2007,22(5):104-110.
[4]吴婷,肖岚,姚志垒.双降压式全桥逆变器[J].中国电机工程学报,2009,29(15):22-27.
Wu Ting,Xiao Lan,Yao Zhilei.Dual buck full-bridge inverter[J].ProceedingsoftheCSEE,2009,29 (15):22-27.
[5]陈新,韦徵,胡雪峰,等.三相并网逆变器LCL滤波器的研究及新型有源阻尼控制[J].电工技术学报,2014,29(6):71-79.
Chen Xin,Wei Zheng,Hu Xuefeng,et al.Research on LCL filter in three-phase grid-connected inverter andnovel active damping control strategy[J].Transactions of China Electrotechnical Society,2014,29(6):71-79.
[6]刘飞,查晓明,段善旭.三相并网逆变器LCL滤波器的参数设计与研究[J].电工技术学报,2010,25 (3):110-116.
Liu Fei,Zha Xiaoming,Duan Shanxu.Design and research on parameter of LCL filter in three-phase grid-connected inverter[J].TransactionsofChinaElectrotechnical Society,2010,25(3):110-116.
[7]李欣然,郭希铮,王德伟,等.基于 LCL滤波的大功率三相电压型PWM整流器[J].电工技术学报,2011,26(8):79-84.
LiXinran,GuoXizheng,WangDewei,etal. Research and development of high-power three-phase voltagesourcePWMrectifierwithLCLfilter[J]. Transactions of China Electrotechnical Society,2011,26(8):79-84.
[8]He Jinwei,Li Yunwei.Generalized closed-loop control schemes with embedded virtual impedances for voltage source converters with LC or LCL filters[J].IEEE TransactionsonPowerElectronics,2012,27(4): 1850-1861.
[9]郑昕昕,肖岚,王长宝,等.三相变流器LCL滤波器参数优化新方法[J].中国电机工程学报,2013,33(12):55-63.
Zheng Xinxin,Xiao Lan,Wang Changbao,et al.A new parameter optimization method of LCL filters in three-phase converters[J].Proceedings of the CSEE,2013,33(12):55-63.
[10]Sun Pengwei,LiuChuang,LaiJih-Sheng,etal. Three-phase dual-buck inverter with unified pulse width modulation[J].IEEE Transactions on Power Electronics,2012,27(3):1159-1167.
[11]洪峰,单任仲,王慧贞,等.一种新型的磁集成双Buck逆变器[J].电工技术学报,2007,22(6): 76-81.
Hong Feng,Shan Renzhong,Wang Huizhen,et al.A novel dual buck inverter with integrated magnetics[J]. Transactions of China Electrotechnical Society,2007, 22(6):76-81.
[12] 谢江华,张方华,王旭东.三电感双 Buck逆变器[J].中 国 电 机 工 程 学 报,2014,34(21): 3413-3422.
Xie Jianghua,Zhang Fanghua,Wang Xudong.A threeinductordual-buckinverter[J].Proceedingsofthe CSEE,2014,34(21):3413-3422.
[13]Sun P,Chen C L,Lai J S,et al.Cascade dual-buck full-bridge inverter with hybrid PWM technique[C]// The 27th Annual Conference of IEEE Applied Power Electronics Conference and Exposition(APEC),Orlando,2012:113-119.
[14]Sun Pengwei,LiuChuang,LaiJih-Sheng,etal. Cascade dual buck inverter with phase-shift control[J]. IEEE Transactions on Power Electronics,2012,27(4): 2067-2077.
[15]Salmon J,Knight A M,Ewanchuk J.Single-phase multilevelPWMinvertertopologiesusingcoupled inductors[J].IEEE Transactions on Power Electronics,2009,24(5):1259-1266.
[16] 郑昕昕,肖岚,田洋天,等.一种半周期SVPWM控制的三相双向双Buck/Boost变流器[J].中国电机工程学报,2013,33(15):19-28.
Zheng Xinxin,Xiao Lan,Tian Yangtian,et al.Halfcycle SVPWM controlled three-phase bidirectional dual buck/boost converters[J].Proceedings of the CSEE,2013,33(15):19-28.
[17] 祁琦.三相双降压逆变器及其滤波器磁集成技术的研究[D].南京:南京航空航天大学,2014.
[18] (美)麦克莱曼.变压器与电感器设计手册[M].龚绍文(译).北京:中国电力出版社,2008.
吕林娜女,1994年生,博士研究生,研究方向为电力电子变换技术。
E-mail:linna0309@126.com(通信作者)
肖岚女,1971年生,教授,博士生导师,研究方向为航空电源系统,功率变换技术等。
E-mail:xiaolan@nuaa.edu.cn
Comparison and Optimal Design for Magnetic Integration Methods of Inductors in Three-Phase Dual-Buck Inverters
Lü LinnaXiao LanQi Qi
(Jiangsu Key Laboratory of New Energy Generation and Power Conversion Nanjing University of Aeronautics&AstronauticsNanjing210016China)
The three-phase dual-buck inverter has higher reliability as it overcomes the straight-leg problem existing in the traditional bridge inverter.However,many output filtering inductors are needed in the topology,which causes bulk capacity.Magnetic integration is a good way to reduce the volume and weight of the magnetic components and improve the power density of the system.In this paper,analysis of different integration methods is carried out considering inductor coupling.The circuit principles are utilized to discuss the possibilities of various methods and the effects of the inductors to the current fed to the grid.Based on the discussion,an optimized method is proposed to integrate the inductors in an incomplete-coupling way with connected dotted terminals,whose equivalent three inductors has identical characteristics with those of the two inductors in the traditional dual-buck topology.This method is better in aspects of the volume and filtering effects in comparison with the existed integration methods and discrete inductors.Finally the theory is validated by a 15kV·A three-phase dual-buck grid-connected inverter prototype.The experiment results are in consistent with the analysis.
Magnetic integration,dual-buck,three-phase inverter,coupled inductor
TM464
国家自然科学基金(51377082)、江苏省“青蓝工程”和江苏省高校优秀科技创新团队资助项目。
2015-04-06改稿日期 2015-08-07

