基于载波移相控制的高功率密度双降压式全桥逆变器

谢江华　张方华　张　帅　陈　菲　雷　鸣（江苏省新能源发电与电能变换重点实验室（南京航空航天大学） 南京　210016）



基于载波移相控制的高功率密度双降压式全桥逆变器

谢江华张方华张帅陈菲雷鸣
（江苏省新能源发电与电能变换重点实验室（南京航空航天大学） 南京210016）

双降压式全桥逆变器（DBFBI）因不存在桥臂直通、直流利用率高而且可实现续流二极管的最优选取，所以具有可靠性高和变换效率高方面的优势。但是，DBFBI具有四个滤波电感，体积重量较大，限制了其在高功率密度场合的应用。将载波移相SPWM（CPS-SPWM）的控制方法应用到DBFBI中，该控制方式下，输出滤波电感等效工作频率是开关频率的两倍，有效地减小了滤波电感的体积和重量。此外，在电感电流半个周期内高频状态时只有两个开关管工作，有效地降低了逆变器的开关损耗。详细地分析了该控制方式下环流产生的原因，通过从原有的4个滤波电感中分离出一个共用的滤波电感（CFI），有效地减小了环流损耗，并且给出了滤波电感的具体的设计过程。最后将剩余的四个滤波电感两两耦合，进一步提高了磁心的利用率。实验结果验证了理论分析的正确性。

双降压式全桥逆变器载波移相SPWM环流滤波电感耦合电感

0　引言

在分布式电源系统、UPS、航空二次电源和电动汽车等领域，逆变器发挥着重要的作用［1-4］。桥式逆变器被广泛地应用在这些领域，然而桥式逆变器开关管的寄生二极管的反向恢复电流大，会产生很大的开关损耗，限制了开关频率的提高［4-8］。此外，桥式逆变器还存在桥臂直通的问题，大大降低了逆变器的可靠性。为了提高逆变器的可靠性，文献［9］提出了一种双Buck半桥逆变器（Dual Buck Inverter，DBI）［10-12］，该逆变器不存在桥臂直通和开关管寄生二极管反向恢复问题，可靠性高，可大幅度提高开关频率。但DBI的输入直流电压利用率较低，增加了功率管的电压应力。文献［13］提出了一种双降压式全桥逆变器［12-17］，该逆变器除了具有DBI高可靠和高效率的优点，还解决了DBI输入直流电压利用率低的问题，并且输入电容电压脉动频率为DBI的2倍，输入电容可适当减小。但是该逆变器的4个滤波电感上的电流是半周期正弦波，磁心单相磁化，磁性元件利用率偏低，体积重量较大。

为此，本文将载波移相SPWM控制方法应用到DBFBI中，在输出电感电流半周内，只有两个开关管高频开关，因此开关损耗较少，且这两个开关管驱动移相180°，使得输出滤波电感电流频率加倍，从而滤波电感减小为原来的一半。但该控制方式下会有环流产生，为了减小该控制方法带来的环流损耗，从原来4个滤波电感中分离出一个共用的滤波电感。同时，该共用的滤波电感流过双向电流，电感磁心能够被双向磁化，磁心利用率得到有效地提高。最后将剩余的4个电感两两耦合，这样耦合电感磁心同样双向磁化，进一步提高了整个滤波电感的体积重量。另外，本文定量分析了支路电感取值与损耗的关系，通过合理地设计滤波电感，使得逆变器的损耗最小。

1　工作原理

图1为基于CPS-SPWM控制的DBFBI主电路。其中 S1、S2、S3、S4为主功率开关管，VD1、VD2、VD3、VD4为续流二极管，L1、L2、L3、L4为输出滤波电感，Cf为输出滤波电容，iLf为电感 L1、L2电流之和，uof为输出电压的采样信号，iLf为输出电流的采样信号，iref为电压环的输出信号，ur为电流环的输出信号，uc为三角载波信号，ugs1、ugs2、ugs3、ugs4分别为S1、S2、S3、S4的驱动信号。输出滤波电感电流和输出电压正方向如图1所示。图2为S1～S4驱动波形示意图。由图2可知该逆变器工作于半周期运行模式，即在输出滤波电感电流半周期内只有S1（S2）、S4（S3）高频开关，并且S1（S2）、S4（S3）之间移相180°。由于iLf为正和负时逆变器工作原理类似，因此本文仅分析iLf为正时的工作模态。DBFBI的开关模态和关键波形如图3和图4所示。

图1　基于CPS-SPWM控制的DBFBI主电路Fig.1　Main circuit of the DBFBI of the DBFBI with the proposed CPS-SPWM control

为了便于分析做如下假设:①所有的功率器件均为理想器件；②4个滤波电感相同，即L1=L2=L3=L4。

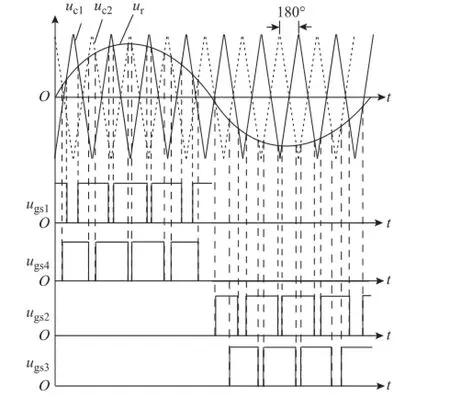
图2　S1～S4驱动波形示意图Fig.2　Drive schematic diagram of S1～S4

模态1［t0，t1］:等效电路如图3a所示。在t0时刻开关管S1、S4导通，电感L1、L4上的电压VL1=VL2= （Vin-vo）/2，电感电流iL1、iL2线性上升，当开关管S4关断时该工作模态结束。

模态2［t1，t2］:等效电路如图3b所示。在t1时刻开关管S4关断，二极管VD4导通续流。此时VD2承受正压导通，加在电感L2上的电压为

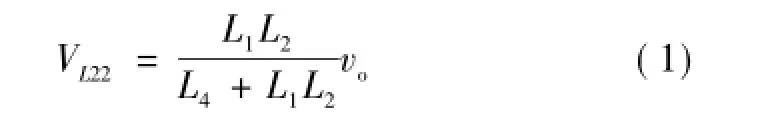
流过L2的电流iL2由零线性上升。此时会有环流流过S1、L1、L2和VD2。而电感L1和L4两端的电压VL1=-VL2、VL4=-2VL2，所以电感L4电流下降的斜率是L1电流的2倍。当S4开通时该工作模态结束。

模态3［t2～t3］:等效电路如图3c所示。在t2时刻S4开通，二极管VD4关断。此时加在L2两端的电压VL2为

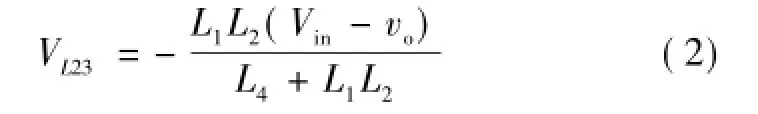
电流iL2线性下降。电感L1和L4两端的电压分别是VL1=-VL2、VL4=-2VL2，所以电感L4电流线性上升，斜率是 L1的2倍。当 iL2下降到零时该工作模态结束。

模态4［t3，t4］:等效电路如图3d所示。在t3时刻iL2下降到零，二极管VD2承受反压截止，流过电感L1、L4的电流以相同的斜率线性上升。

模态5［t4，t5］、模态6［t5，t6］、模态7［t6，t7］的分析可参考前面模态的分析，不再赘述。

图3　DBFBI的开关模态Fig.3　Switching modes of DBFBI

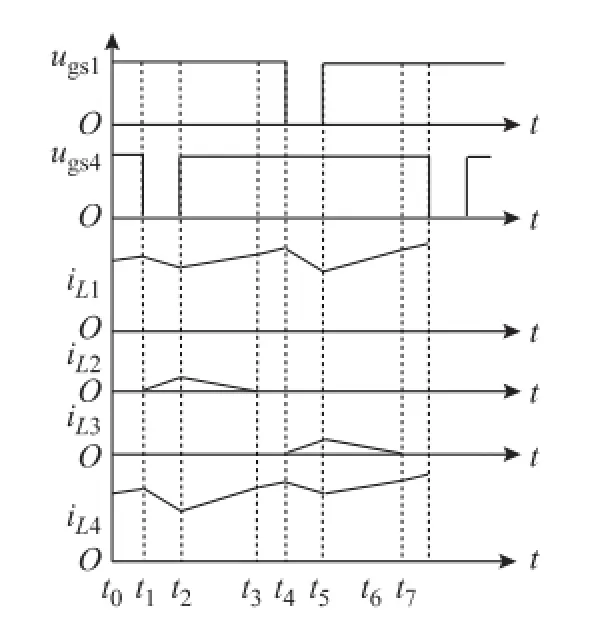
图4　DBFBI的关键波形Fig.4　Main waveforms of the DBFBI

2　环流分析

2.1环流产生的原因及影响因素

由第1节分析可知，环流主要存在于模态2、3、5和6。其中模态2、3和模态5、6类似。以模态2、3为例进行分析。

设总的滤波电感为Lf，其中L1=L2=L3=L4= Lf/2=L，结合式（1）和图3b可得环流电流上升的斜率λc1为

由于该逆变器采用SPWM调制，因此其占空比是按正弦规律变化的，设其占空比D（i）为

D（i）=Msinα（i）（6）

式中，M为常数；α（i）为ugs1第i个时段中心点相位。

设Ia为iL2在t1～t3的平均值，则Ia为

由图4和式（7）可以得到环流有效值Icc为

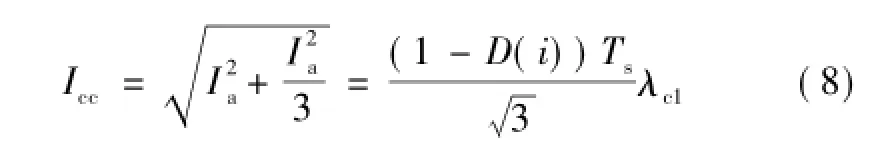
由式（8）可知，环流量的大小与占空比D（i）、开关周期Ts以及环流的上升斜率有关。而前两个量与逆变器的控制有关，在单个开关周期内可认为是定值。而环流的上升斜率与加在电感两端的电压以及电感值的大小有关。

2.2减小环流的方法

为了减小环流的上升斜率，降低逆变器环流损耗，从原来的4个滤波电感中分离出一个共同的滤波电感LCf，则带共用电感的DBFBI电路如图5所示。由于LCf的分离使得剩余的滤波电感占总滤波电感的比例减小，从而使得环流电流上升斜率降低。

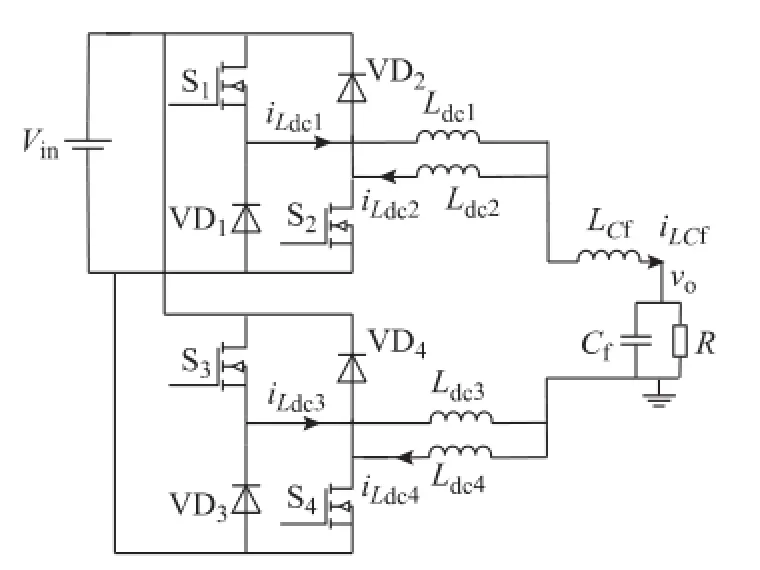
图5　带共用电感的DBFBI电路Fig.5　Circuit of the DBFBI with a CFI

设总的滤波电感为Lf，支路电感Ldc1=Ldc2=Ldc3= Ldc4=kL（0≤k≤1），Ldc1+Ldc4+LCf=Lf，其中 L= Lf/2。带LC f的DBFBI环流电流上升斜率为

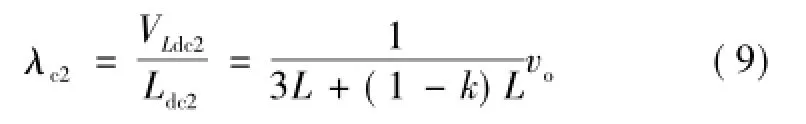
对比式（5）和式（9）可知λc2＜λc1，且k越小环流电流上升斜率越小，环流越小。因此，CFI的加入能有效地减小环流损耗，且CFI越大环流损耗越小。同时，该滤波电感上的电流为完整的交流正弦波，磁心双向磁化，磁心利用率得到提高。

2.3滤波器的设计方法

2.3.1环流损耗计算

根据式（8）、式（9）可知，支路电感越小，逆变器环流损耗越小。设k1、k2分别为流过电感Ldc2环流电流的上升斜率和下降斜率。

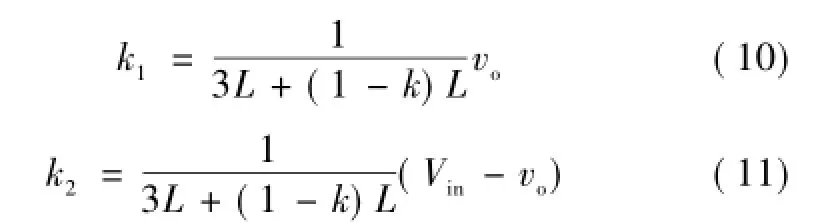
流过电感Ldc2环流电流上升和下降的时间tc1和tc2分别为

环流的出现会产生额外的损耗。根据前文分析，模态2、3和模态5、6类似，都会出现环流，因此本文只分析模态2、3的环流附加损耗。在模态2、3中，额外的损耗主要有开关管S1的导通附加损耗pS1con、二极管VD2的导通附加损耗pVD2con以及电感L1、L2的导通附加损耗pL1Cu、pL2Cu。

开关管S1导通附加损耗pS1con为

式中，fout为逆变器输出频率；Ns为开关管在一个周期内的开关次数；Rdson为开关管导通电阻；iLdc1（i）、iLCf（i）分别为第i次时电感电流有效值。

续流二极管VD2导通附加损耗pVD2con为

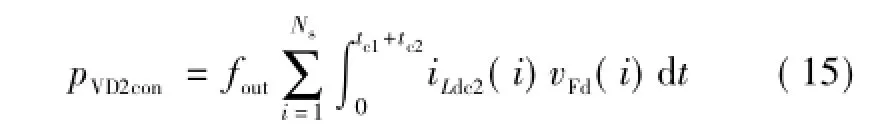
式中，vFd（i）为续流二极管VD2导通压降。

支路电感Ldc1和Ldc2的附加损耗pL1Cu和pL2Cu分别为

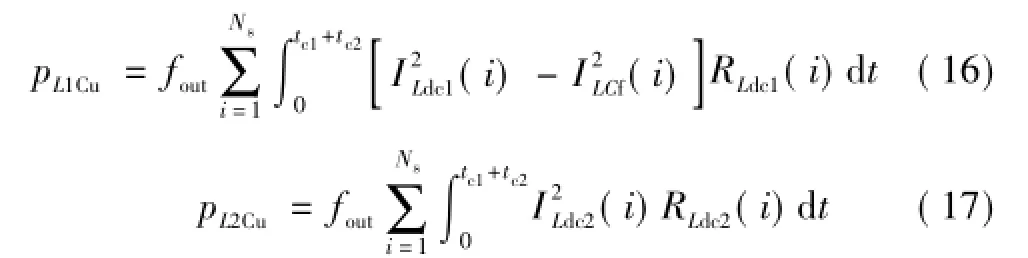
式中，RLdc1（i）、RLdc2（i）分别为滤波电感Ldc1和Ldc2的直流电阻。

总的环流附加损耗p_cc为

图6给出了输入电压为 180 V，输出电压为115 V，输出功率为1 kV·A时总环流附加损耗p_cc和支路电感取值关系。由图6可见，支路电感值越小，附加损耗越小。环流损耗最大为8.1 W左右。

图6　总环流附加损耗p_cc和支路电感取值关系Fig.6　The relationshipof the total circulating current additional losses p_ccand the DC filter inductor

2.3.2谐振损耗计算

为减小环流损耗，支路电感的值越小越好。但当支路电感的值减小到一定程度时，支路电感与功率管的寄生电容的谐振过程就无法被忽略了［21］。因此要考虑谐振损耗对逆变器效率的影响。

功率器件的寄生电容和支路电感的谐振过程主要产生于各个开关管开通或者关断的切换过程中，其中以S1开通和关断时产生的谐振现象进行分析，图7为电感谐振电流示意图，其他类似。开关管S1开通时，Ldc2和CVD2、CS2谐振，CVD2放电，CS2充电，电感电流iLdc2谐振上升。当 CVD2电压放电至零时，二极管VD2导通，电感电流iL dc2谐振下降，直到零时结束。开关管S1关断时，Ldc2和CVD2、CS2谐振，CS2放电，CVD2充电，电感电流iLdc2反向谐振上升。当CS2电压放电至零时，开关管S2的体二极管CS2导通，电感电流iLdc2反向谐振下降，直到零时结束。

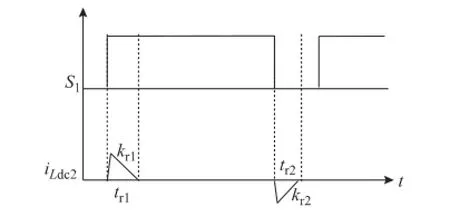
图7　电感Ldc2谐振电流示意图Fig.7　The resonant current schematic diagram of Ldc2

由于支路电感的大小直接影响谐振电流的大小，从而影响谐振附加损耗的大小，因此需要定量分析支路电感对谐振损耗的影响。支路电感和谐振损耗的关系推导可参见文献［21］。附录给出了具体的推导过程。

图8给出了输入电压为 180 V，输出电压为115 V，输出功率为1 kV·A时总谐振附加损耗pr和支路电感取值关系。

图8　总谐振附加损耗pr和支路电感取值关系Fig.8　The relationship of the resonant additional losses prand the DC filter inductor

图8可以看出，支路电感值越小，附加谐振损耗越大，因此支路电感的选取必须综合环流损耗和谐振损耗来选取。总的附加损耗p_sum为

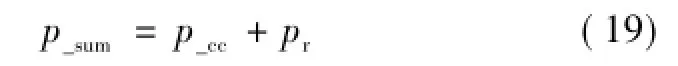
根据式（19）可作出总附加损耗p_sum和支路电感取值关系，如图9所示。当支路电感取10 μH时，附加损耗最小为3.54 W。说明CFI的加入有效减小了该逆变器的环流损耗。

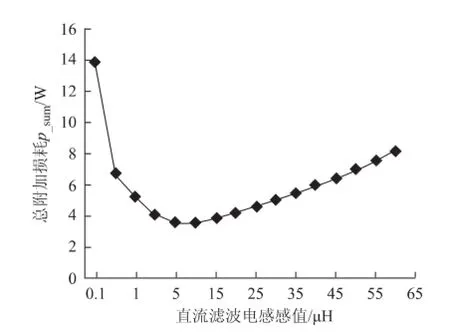
图9　总附加损耗p_sum和支路电感取值关系Fig.9　The relationship of the total additional losses p_sumand the DC filter inductor

3　耦合电感分析

图10为带耦合电感的DBFBI等效图，该耦合电感解耦后与前面所述的电路工作原理完全一致，区别仅在于解耦后等效支路电感为Ldc1+M、Ldc2+M、Ldc3+M、Ldc4+M，CFI变为LCf-M，其中M为互感。

将平均粒径18 μm重质碳酸钙分别在900、1 000、1 100、1 200 ℃下煅烧4 h，后采用冶金石灰物理检验方法对石灰活性进行测试，结果如图1所示。

图10　带耦合电感的DBFBI等效图Fig.10　The DBFBI with coupled inductors

4　实验结果分析

基于载波移相的DBFBI原理样机参数为:开关管采用IPP200N25N3G；续流二极管采用DPG30C300PB；直流输入电压为180 V；输出电压为AC 115 V/400 Hz；输出耦合支路电感采用异名端相连耦合；耦合系数

k=1；等效输出支路电感为 Ldc1=Ldc2=Ldc3=Ldc4= 10 μH；等效共用滤波电感LCf=100 μH；输出滤波电容为6.6 μH；开关频率为40 kHz。表1为采用载波移相控制的DBFBI和传统DBFBI两种逆变器滤波电感参数比较，其中，LCoupled1和 LCoupled2分别为 Ldc1、Ldc4和Ldc2、Ldc3两两耦合后的耦合电感；L为传统DBFBI的滤波电感。由表1可知，前者相对于后者磁心体积减小了63.3%，重量减轻了428 g，减重比例达到了60.5%。

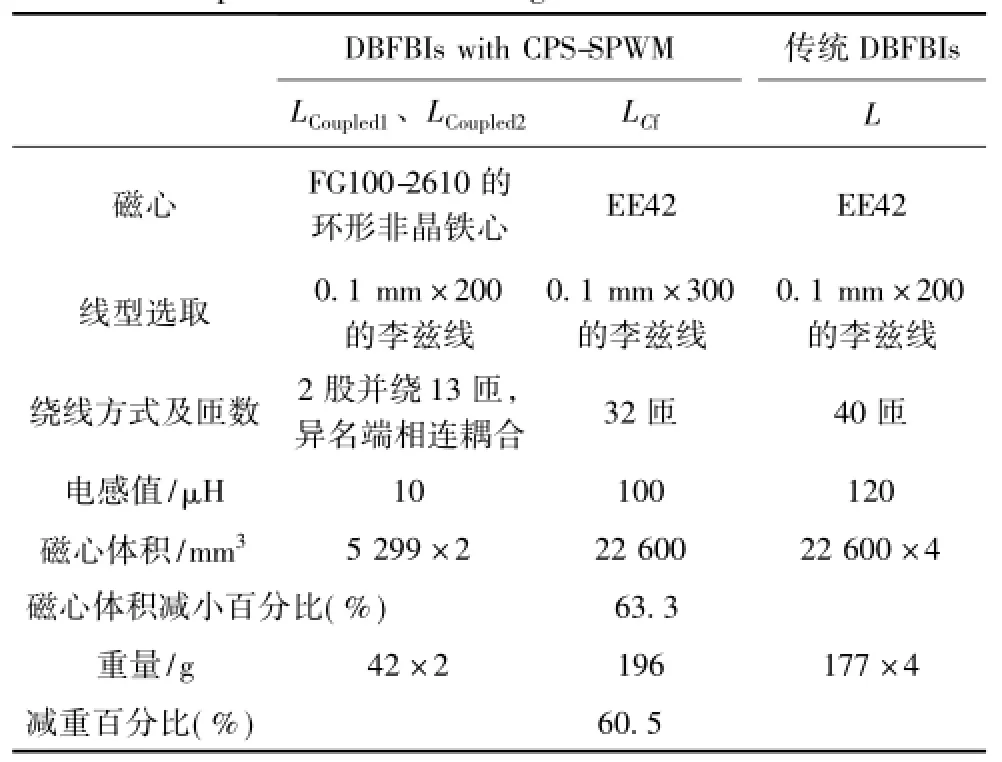
表1　两种逆变器滤波电感参数比较Tab.1　Comparison of the filtering inductor o f the two inverters

图11为基于载波移相的DBFBI阻性满载实验波形，图11中，vbus为母线电压；iLdc1为支路电感Ldc1的电流；iLCf为共用滤波电感电流；vout为输出电压。由图11可知，共用滤波电感LCf正负半周交替工作，输出波形良好，THD为0.6%。

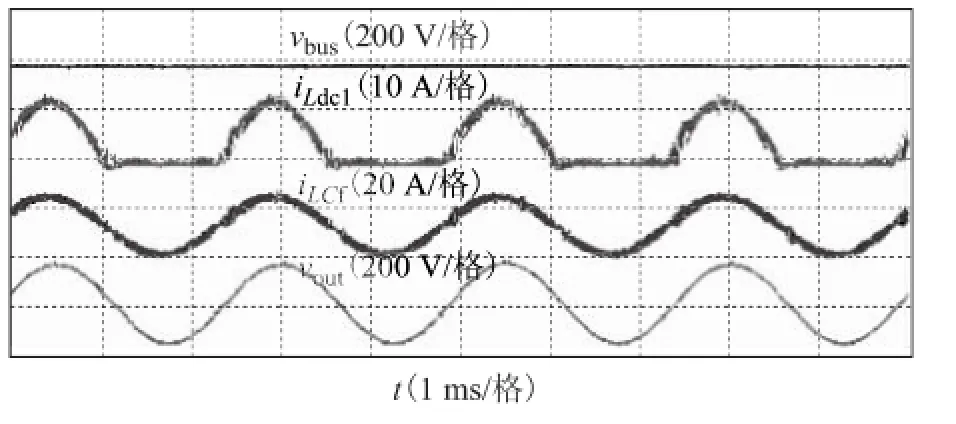
图11　阻性满载实验波形Fig.11　Experimental waveforms with full resistive load

图12a和图12b分别为电感 Ldc1、LCf和 Ldc2、Ldc3的电流实验波形。图12中，ugs1和ugs4分为S1和S4的驱动信号；iLdc1和iLCf为滤波电感Ldc1和LCf的电流；iLdc2和iLdc3为滤波电感Ldc2和Ldc3的电流。由图12a可知，电感电流iLdc1和iLCf的等效工作频率为开关频率的2倍。由图12b可知，当S1开通和关断时，电感电流iLdc2会有谐振电流产生，当S4开通和关断时，电感电流iLdc3会有谐振电流产生。同时，从实验波形也可以很明显地看到环流电流同时存在于电感电流iLdc2和iLdc3中，与理论分析一致。

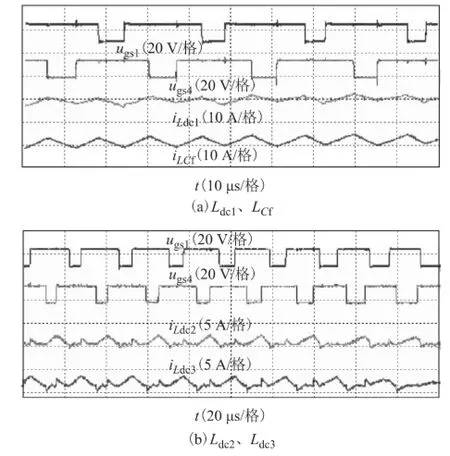
图12　电感电流实验波形Fig.12　Experimental waveforms of inductor current

根据前面的理论分析可知当支路电感由60 μH降为10 μH时，逆变器理论计算总的附加损耗会减少4.6 W。图13给出了在不同的支路电感下，该逆变器的效率曲线。由图13可知，当支路电感由60 μH降为10 μH时，逆变器满载效率提升了0.46个百分点，实验结果与理论分析一致。说明通过合理的优化设计支路电感的值可以使得逆变器总的附加损耗最小。该逆变器具有较高的效率，满载时效率达到97.8%左右。

图13　效率曲线Fig.13　Efficiency curves

5　结论

附录

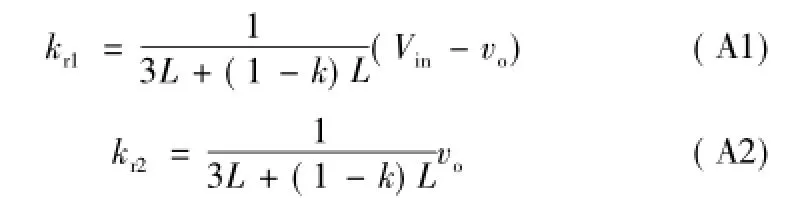
tr1、tr2分别为S1开通和关断时谐振过程持续的时间

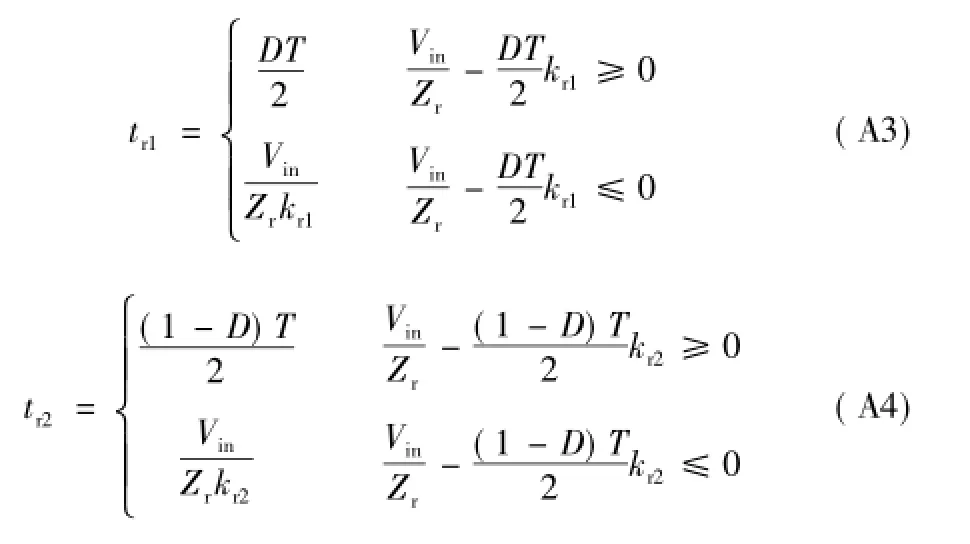
开关管S1开通时谐振附加损耗主要包括:开关管S1的导通损耗pS1on续流二极管VD2的导通损耗pVD2on和支路电感损耗pLCu1。

开关管S1导通附加损耗为

二极管VD2的导通附加损耗为

电感Ldc1和Ldc2导通附加损耗

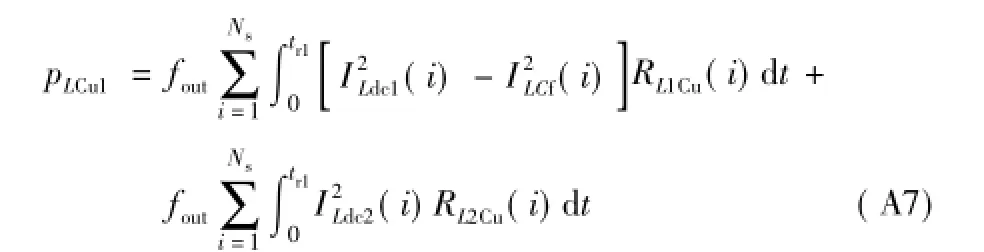
开关管S1关断时谐振附加损耗主要包括:开关管S2体二极管VDS2导通损耗pSVD2on，续流二极管VD1的导通损耗pVD1on和支路电感铜耗pL Cu2。

开关管S2体二极管导通附加损耗为

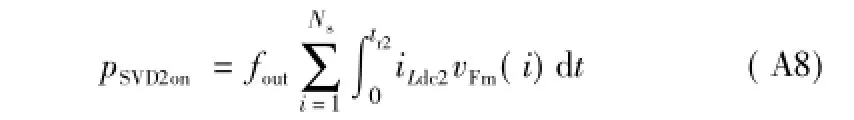
式中，vFm为开关管S2体二极管的导通压降。

二极管VD1的导通附加损耗为

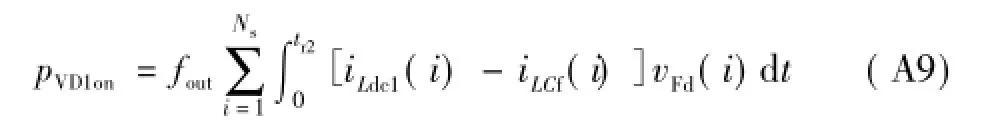
电感Ldc1和Ldc2导通附加损耗为

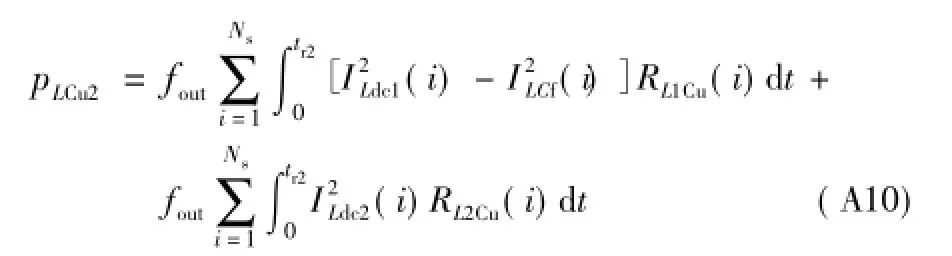
由于4个开关管的在开关过程中都会产生谐振附加损耗，因此逆变器总附加损耗pr为

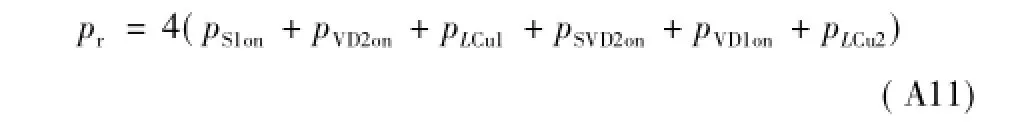
［1］Shafiee S，Fotuhi-Firuzabad M，Rastegar M.Investigating the impacts of plug-in hybrid electric vehicles on power distribution systems［J］.IEEE Transactions on Smart Grid，2013，4（3）:1351-1360.

［2］杨晓光，姜龙斌，冯俊博，等.一种新型高效无变压器型单相光伏逆变器［J］.电工技术学报，2015，30（8）:97-103.

Yang Xiaoguang，Jiang Longbin，Feng Junbo，et al.A new high efficiency transformerless single-phase photovoltaic inverte［J］.Transactions of China Electrotechnical Society，2015，30（8）:97-103.

［3］雷亚雄，李建文，李永刚.基于准PR调节器电流双闭环LCL三相并网逆变器控制［J］.电力系统保护与控制，2014，42（12）:44-50.

Lei Yaxiong，Li Jianwen，Li Yonggang.Control strategy of three-phase LCL grid-connected inverter based on quasi-PR adjuster［J］.Power System Protection and Control，2014，42（12）:44-45.

［4］赵拥华，方永毅，王娜，等.逆变型分布式电源接入配电网对馈线自动化的影响研究［J］.电力系统保护与控制，2013，41（24）:117-122.

ZhaoYonghua，FangYongyi，WangNa，etal. Research on the impacts on feeder automation by inverterbased distribution generation connected to the distribution network［J］.PowerSystemProtectionandControl，2013，41（24）:117-122.

［5］尹培培，洪峰，王成华，等.无源无损软开关双降压式全桥逆变器［J］.电工技术学报，2014，29（6）: 40-48.

Yin Peipei，HongFeng，WangChenghua，etal. Passive lossless soft-switching dual buck full bridge inverter［J］.TransactionsofChinaElectrotechnical Society，2014，29（6）:40-48.

［6］王强，王天施，孙海军，等.新型高效率并联谐振直流环节软开关逆变器［J］.电工技术学报，2013，28（5）:219-226.

Wang Qiang，Wang Tianshi，Sun Haijun，et al.Novel high efficiency parallel resonant DC link soft-switching inverter［J］.TransactionsofChinaElectrotechnical Society，2013，28（5）:219-226.

［7］Mezaroba M，Martins D C，Barbi I，et al.A ZVS PWM half-bridge voltage source inverter with active clamping［J］.IEEE Transactions on Industrial Electronics，2007，54（5）:2665-2672.

［8］Wang C M，Su C H，Jiang M C，et al.A ZVS-PWM singlephaseinverterusingasimpleZVS-PWM commutation cell［J］.IEEE Transactions on Industrial Electronics，2008，55（2）:758-766.

［9］Liu Jun，Yan Yangguang.A novel hysteresis current controlled dual buck half bridge inverter［C］//Power Electronics Specialist Conference，Acapulco，Mexico，2003:1615-1620.

［10］ 刘苗，洪峰，尹培培，等.复合型级联双Buck飞跨电容五电平逆变器［J］.电工技术学报，2015，30 （18）:35-42.

Liu Miao，Hong Feng，Yin Peipei，et al.A hybrid cascaded dual Buck flying-capacitor five-level inverter［J］.Transactions of China Electrotechnical Society. 2015，30（18）:35-42.

［11］ 嵇保健，赵剑锋，洪峰.一种新颖的三电平双Buck逆变器［J］.电工技术学报，2011，26（增1）: 148-153.

Ji Baojian，Zhao Jianfeng，Hong Feng.A novel threelevel dualBuckinverter［J］.TransactionsofChina Electrotechnical Society，2011，26（S1）:97-101.

［12］ 马海啸，陈凯，龚春英.双Buck逆变器的建模与优化设计［J］.电工技术学报，2012，27（8）:35-41.

Ma Haixiao，Chen Kai，Gong Chunying.Modeling and optimization design of dual-buck inverter［J］.Transactions of China Electrotechnical Society，2012，27（8）:35-41.

［13］ 吴婷，肖岚，姚志垒.双降压式全桥逆变器［J］.中国电机工程学报，2009，29（15）:22-27.

Wu Ting，Xiao Lan，Yao Zhilei.Dual buck full-bridge inverter［J］.Proceedings of the CSEE，2009，29（15）: 22-27.

［14］Sun Pengwei，Chien-Liang Chen，Lai Jih-Sheng，et al. Cascade dual-buck full-bridge inverter with hybrid PWM technique［C］//Applied Power Electronics Conference and Exposition（APEC），Florida，2012:113-119.

［15］Yao Zhilei，Xiao Lan，Yan Yangguang.Dual-buck fullbridge inverter with hysteresis current control［J］.IEEE Transactions on Industrial Electronics，2009，56（8）: 3153-3160.

［16］Yao Zhilei，Xiao Lan，Wei Xing，et al.Dual-buck full-bridge inverter with SPWM control and single current sensor［C］//IndustrialElectronicsandApplications （ICIEA），Taichung，Taiwan，2010:2154-2158.

［17］洪峰，单任仲，王慧贞，等.五电平双降压式全桥逆变器［J］.电工技术学报，2008，23（8）:67-73.

Hong Feng，Shan Renzhong，Wang Huizhen，et al.A novel dualbuckfullbridgefive-levelinverter［J］. Transactions of China Electrotechnical Society，2008，23（8）:67-73.

［18］Yao Zhilei，Xiao Lan，Wei Xing，et al.A highreliability and high-efficiency off-grid inverter suitable for direct-driven wind generator systems［C］//Power and Energy Engineering Conference（APPEEC），Chengdu，China，2010:1-3.

［19］Yao Zhilei，Hu Guowen.Comparison of dual-buck fullbridge inverter with different inductor structures［C］// Power and Energy Engineering Conference（APPEEC），Wuhan，China，2011:1-3.

［20］Chen Baifeng，Sun Pengwei，Liu Chuang，et al.High efficiency transformerless photovoltaic inverter with widerangepowerfactorcapability［C］//AppliedPower Electronics Conference and Exposition（APEC），Florida，2012:575-582.

［21］谢江华，张方华，王旭东.三电感双buck逆变器［J］.中国电机工程学报，2014，24（21）:3413-3422.

XieJianghua，ZhangFanghua，WangXudong.A three-inductor dual-Buck inverter［J］.Proceedings of the CSEE，2014，24（21）:3413-3422.

［22］ 张方华，龚春英，邓翔.航空静止变流器的研究综述［J］.南京航空航天大学学报，2014，46（1）: 19-26.

Zhang Fanghua，Gong Chunying，Deng Xiang.Review of aeronauticstaticinverter［J］.JournalofNanjing University of Aeronautics and Astronautics，2014，46 （1）:19-26.

谢江华男，1989年生，硕士，研究方向为功率电子变换技术。

E-mail:352225908@qq.com

张方华男，1976年生，教授，博士生导师，研究方向为电力电子技术、可持续能源发电及并网控制技术、航空电源、半导体照明驱动技术。

E-mail:zhangfh@nuaa.edu.cn（通信作者）

A High Power Density Dual-Buck Full-Bridge Inverter Based on Carrier Phase-Shifted Control

Xie JianghuaZhang FanghuaZhang ShuaiChen FeiLei Ming
（Jiangsu Key Laboratory of New Energy Generation and Power ConversionNanjing University of Aeronautics and AstronauticsNanjing210016China）

The dual buck full-bridge inverter（DBFBI）has great advantages in reliability and efficiency because of no shoot-through concerns，high utilization rate of DC input voltage，and optimal choice of its free-wheeling diodes.However，the four filter inductors make the inverter large and heavy，which limits its applications in high power density conditions.The carrier phase-shifted sinusoidal pulse width modulation（CPS-SPWM）control is applied to DBFBIs in this paper.With the CPS-SPWM control，the equivalent operating frequency of the output filter inductors is twice of the switching frequency，which effectively reduces the size and weight of the filter inductor.In addition，only two switches work in the high-frequency switching state during the half line cycle of the filter-inductor current，which can effectively reduce the inverter switching losses.The circulating current introduced by this control is analyzed in detail.By separating a common filter inductor（CFI）from the four primary inductors，the circulating current losses can be effectively reduced.The design guidelines of the filter inductors are provided.Finally，the remaining four filter inductors are realized by two coupled inductors in order to further utilize the magnetic core.Experimental results verify the theoretical analysis.

Dual buck full-bridge inverter，carrier phase-shifted SPWM，circulating current，filter inductor，coupled-inductor

TM464

国家自然科学基金资助项目（51007039）

2014-07-18改稿日期 2014-08-14