基于改进均压算法的模块化多电平变流器开关频率分析

黄守道　廖　武　高　剑　黄　晟　荣　飞（湖南大学电气与信息工程学院　长沙　410082）



基于改进均压算法的模块化多电平变流器开关频率分析

黄守道廖武高剑黄晟荣飞
（湖南大学电气与信息工程学院长沙410082）

以一种优化的最大电压偏差均压方法为基础，推导出模块化多电平变流器（MMC）平均开关频率的解析表达式，并分析了影响MMC开关频率的因素，对MMC损耗计算和散热设计具有一定的指导意义。在Matlab/Simulink平台上建立46电平的单相MMC模型，并进行仿真，最后搭建了9电平单相MMC实验样机，实验结果验证了所得结论的正确性。

模块化多电平变流器开关频率优化均压柔性直流输电

0　引言

基于电压源变流器的直流输电系统具有功率因数可调、可四象限运行、且具有黑启动能力等优点，可用于新能源发电接入以及城市环网供电等场合［1，2］。但采用传统两电平变流器需要采用多个大功率半导体器件串联实现高压交直流转换，存在器件开关应力大、串联均压难、电磁干扰大等缺点。模块化多电平变流器（Modular Multilevel Converter，MMC）具有输出电平数高、谐波小、可利用低压器件串联得到高电压等级以及模块化设计等优点［3-6］，于2002年由德国联邦大学提出后就成各国学者研究的热点。

由于MMC采用多个子模块级联的形式，其调制方法与传统两电平的电压源型变流器 （Voltage Source Converter，VSC）有很大不同，需要加入保证每个子模块电容电压平衡的均压控制算法。基于空间矢量调制（Space Vector Pulse Width Modulation，SVPWM）的MMC由于开关矢量选择众多，算法复杂［7］，在模块化多电平中实现困难。基于载波移相的正弦波调制（Carrier Phase Shifted-Pulse Width Modulation，CPSPWM）的方法每个子模块都需要一个相位一定的载波［8］，均压控制需增加额外的电压控制环，对于子模块数很多的场合其应用受到限制（如西门子的Trans Bay Cable Project工程，每个桥臂达216个子模块［9］）。而基于最近电平逼近调制（Nearest Level Modulation，NLM）方法，只需通过选择投入子模块数来逼近给定电压，特别适合于子模块数很多的MMC调制。其均压方法是根据子模块电容电压大小的情况和桥臂电流方向，利用子模块的冗余度，得到最终需投入的子模块。但此方法会造成子模块的开关频率不固定，并且子模块的开关频率还具有很大的优化空间。为此许多文献对基于最近电平逼近的均压优化方法进行了研究，文献［10，11］提出了基于子模块虚拟电容电压的优化均压策略，根据桥臂电流的方向，在子模块电容电压实际值基础上增加或减去一个偏移量，使子模块具有保持原来通断状态的能力。文献［12］通过引入保持因子使子模块具有一定的保持原来投切状态的能力，以降低开关器件的开关频率。文献［13-15］引入子模块间最大电压偏差量，有效避免了因排序算法导致的同一子模块不必要的反复投切现象。文献［16，17］不考虑子模块之间的电压偏差，在桥臂子模块数改变时，投入或切出电压最高或最低的子模块，可以使开关频率接近基频，但会造成子模块电容电压的过大波动。

综上所述，子模块电容电压的均衡度与开关频率存在矛盾，电容电压允许偏差越大，则开关频率越低；电容电压允许偏差越小，则开关频率越高。因此深入研究子模块开关频率与电容电压均衡度及其他因素之间的关系，可为MMC的均压控制算法实现和损耗分析提供一定的理论参考。

本文对采用改进均压方法的MMC的平均开关频率进行了深入研究，在深入分析MMC开关过程的基础上，得到了采用改进均压方法的平均开关频率解析表达式，详细分析了影响MMC开关频率的各种因素，最后通过仿真和实验验证了本文所得结论的正确性。

1　MMC工作原理

1.1MMC基本结构

如图1所示，MMC的每相每个桥臂采用多个子模块串联而成。子模块一般采用半桥和电容C并联的结构。当半桥中的上桥臂IGBT开通时，子模块为投入状态，此时输出电压为电容电压，若桥臂电流为正，会对子模块电容充电，若桥臂电流为负，会对子模块电容放电。当下桥臂IGBT开通时，子模块为切出状态，此时子模块电容电压不变，输出电压为零。上下桥臂之间的电感L可以抑制由于子模块电容电压波动产生的二次环流。

图1　MMC拓扑结构Fig.1　MMC topology diagram

设 ipa、ina分别为上下桥臂电流，其参考方向如图1所示，有

式中，ia为变流器输出电流；idiffa为变流器A相的内部环流。通常将上下桥臂的参考电压upa、una分别取为

通常情况下，设每个电容额定电压大小为Ucap，所以上下桥臂需投入的子模块数为

式中，round函数为四舍五入取整函数。

1.2MMC均压控制原理

传统的均压控制根据上下桥臂电容电压的排序结果，若桥臂电流为充电电流，则开通电容电压最低的npa个子模块；若桥臂电流为放电电流，则开通子模块电压最高的npa个子模块，这样子模块的电容电压就会趋向平衡。为了对传统均压算法所带来的问题进行改进，避免每次由于电容电压的变化而造成的子模块的频繁切换，文献［5-12］对均压算法进行了改进，本文以最大电压偏差法为例进行分析，其均压控制方法如图2所示，其中n表示当前控制周期需要投入的子模块个数，nold表示上一个控制周期需要投入的子模块个数。

图2　改进均压算法示意图Fig.2　Diagram of improved algorithm for voltage balance control

由图2可知，定义最大电压偏差为同一桥臂在同一时刻最大电容电压与最小电容电压的偏差，当其在设置值范围内时，尽量保持子模块原来的状态不变，只有当最大电压偏差超过设置值时，才按传统的均压算法进行控制。

2　MMC子模块开关过程分析

2.1传统均压算法的开关过程分析

影响MMC开关动作的因素可分为两类，第一类为由于MMC输出电压变化需要增加或减少子模块投入的数量，可称为必要的开关动作。在一个工频周期内，必要的开关动作总次数可表示为

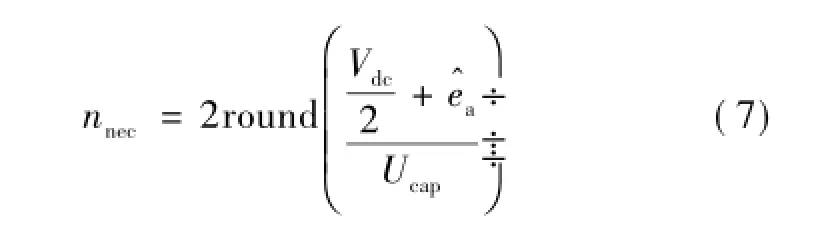
另一类为由于电容电压平衡的需要，在投入子模块数量不变时，按均压的要求交换投入的子模块，可称为附加开关动作，易知附加开关动作必为2的倍数。本文重点对附加开关动作进行分析，以A相上桥臂为例，假设上桥臂子模块数为4，每个子模块的参数一致，桥臂电流为充电电流，在第k个控制周期开始时，电容电压按降序排列后的顺序为SM4、SM3、SM2、SM1，在第k个控制周期结束时，对于投入的子模块，其电容电压根据充放电公式可表示为

式中，ucap［k］为第k个控制周期电容电压；TS为系统的控制周期。根据开通子模块充电后电容电压的情况，则在下个控制周期开始时，会发生子模块的交换。具体交换情况如图3所示，当n=1时，在k+1周期开始时，子模块电容电压的情况如图3a中a、b、c、d四种情况所示，其中a情况下不需要子模块的交换，b、c、d情况下交换数量为2；当n=3时，由互补对称性可知，其情况与n=1时的相同，如图3c所示。当n=2时，在k+1周期开始时，子模块电容电压的情况如图3c中a、b、c、d、e、f六种情况所示，其中a情况下不需要子模块的交换，b、c、d、e情况下交换数量为2，f情况下交换数量最大，即所有子模块状态都要发生交换。

图3　一个控制周期后电容电压分布Fig.3　Diagram of SM voltage after a control period

从以上分析可看出，在传统均压方法下，子模块的状态非常复杂，在每个控制周期结束后，子模块可能的动作次数有多种，最小为零，最大与调制波的值直接相关，可表示为

采用传统均压算法的优点是子模块电容电压的均压效果好，子模块的最大电压偏差一般不会超过每个控制周期的电容电压的变化量。但此方法会额外增加许多附加的开关动作。

2.2优化均压算法开关过程分析

对于图2所示的优化均压方法，开关切换过程为:假设在某一时刻，桥臂电流为充电电流，电容电压刚好超过最大电压偏差，桥臂按普通均压方法投入电压最小的npa个子模块后，再接下来的几个控制周期，除必要的开关动作外，各子模块会保持原来的脉冲状态，所以投入的npa个子模块中最高电压的子模块电压升高到最大，切除状态中的最小电压子模块会变为最小，在最高值与最低值之差达到设定值后，就会进行下一次的子模块均压调整，电容放电时的情况也与之类似。可以看出在每次电压偏差达到最大值时，子模块切换数量可按式（9）计算。当MMC接入真实交流电网时，电网电压由于各种故障，会出现电压突增或突减的情况。由于功率传输的需要，MMC的电压调制比及输出电流也会发生相应变化。根据上文分析可知，优化均压算法在每个控制周期都会对电容电压进行监测，一旦最大电压偏差超过设定值，就会立刻调整相应的子模块，所以此优化算法在电网电压受到干扰时仍然有效。

3　优化均压方法开关频率计算

3.1电压偏差取值范围分析

控制模块由主控芯片、CC1101无线射频模块、继电器电路、电磁开关、各种设备组成，以温室大棚为例，调节设备包括排风扇、CO2发生器、遮阳网电机、加热器、喷淋阀等[11]。控制模块通过继电器控制电磁开关来控制设备。继电器电路中，通过一定宽度的脉冲电信号触发5 V的磁保持继电器，主控芯片I/O口控制三极管Q1来驱动磁保持继电器的闭合，控制三极管Q2驱动磁保持继电器的断开，电路中并联续流二极管1N4148，继电器电路如图3所示。

根据第2节的分析可知，对于图2所示的改进均压方法，Δu的取值影响着器件的开关频率，当Δu取值过小时，优化的均压方法无法起到减少开关动作的作用，过小的Δu会使优化均压方法趋向于传统方法。而当Δu取值过大时，会导致均压效果严重减弱。所以在分析此方法的开关频率时，需结合Δu的取值范围。根据传统的均压方法的原理可知，即使在每个控制周期都依据排序交换子模块，子模块的最大电压偏差也不会为零，而是与控制周期、电容量、桥臂电流大小相关，可表示为

若Δu取值小于式（10）的最大值时，虽然也可得到减少开关频率的效果，但在一个周期内，开关动作的机理会变得不一致，所以本文的分析建立在Δu大于式（10）的最大值基础之上。下面对式（10）的最大值进行计算，根据MMC能量守恒原理，上桥臂电流可表示为

所以，输出电流达到最大峰值时，桥臂电流的绝对值最大，为

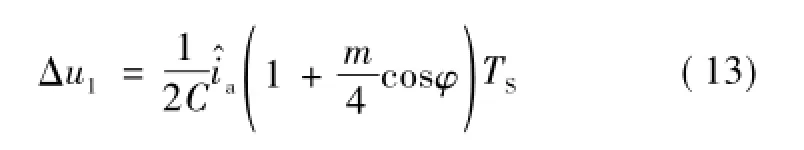
下面分析Δu过大时的情况，若Δu过大，由于必要的开关动作也加入了均压的控制，所以过大的Δu会使附加开关动作变为零，此时子模块的开关频率接近为基频。如图4所示，子模块电容电压在一个工频周期内的最大变化量为

式中，θ1、θ2均为ipa的过零点。根据式（11）易知

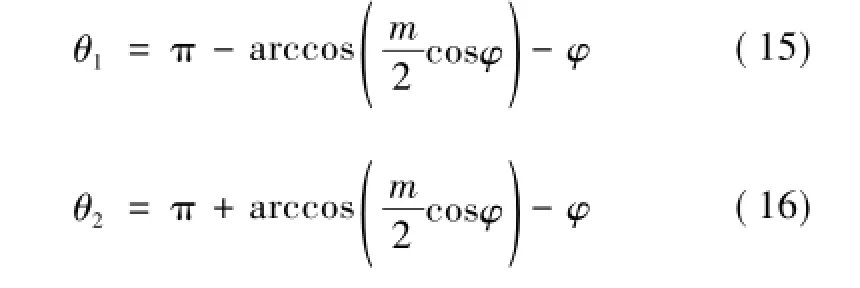
所以式（14）可表示为

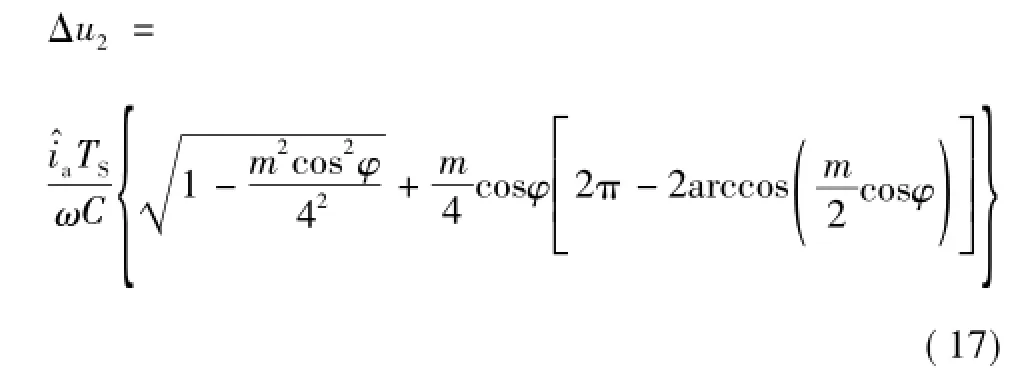
因此，当Δu＞Δu2时，桥臂在一个工频周期的开关次数可按式（7）计算。

3.2开关频率的计算

本文以桥臂整体为研究对象，由于开关频率不固定，首先计算整个桥臂上子模块在一个工频周期内的开关次数，这些开关次数由于均压的作用，会平均分配到每个子模块，从而可得到每个子模块的开关频率。首先假设MMC工作于逆变状态，以上桥臂为例，当Δu1＜Δu＜Δu2时，对于投入的子模块，其电容电压的增量可表示为其桥臂电流与时间轴积分的面积，如图4中阴影部分所示。并且在发生一次子模块投入交换后，电容电压的增量可近似认为Δu，也就是说完成一次交换需要的时间为

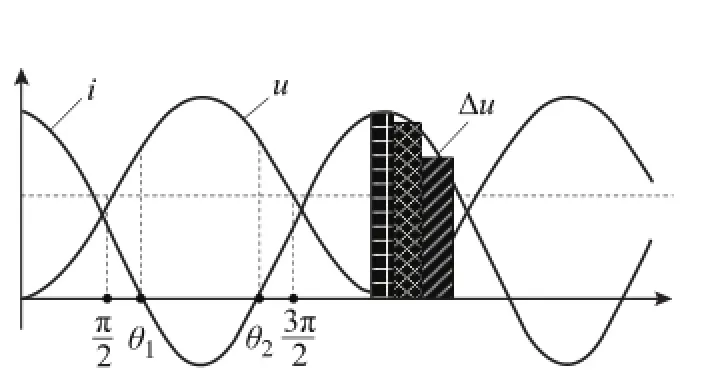
图4　桥臂电流与调制波关系Fig.4　Diagram of arm current and modulation wave

在此段时间内，由于两次开关动作对应一个开关周期，所以桥臂上N个器件的平均开关频率可表示为

因此在一个工频周期内，桥臂上子模块总开关次数可表示为

式中，T为工频周期。由于均压控制的作用，桥臂上的总开关次数会平均分配到每个子模块，所以每个子模块的平均开关频率可表示为

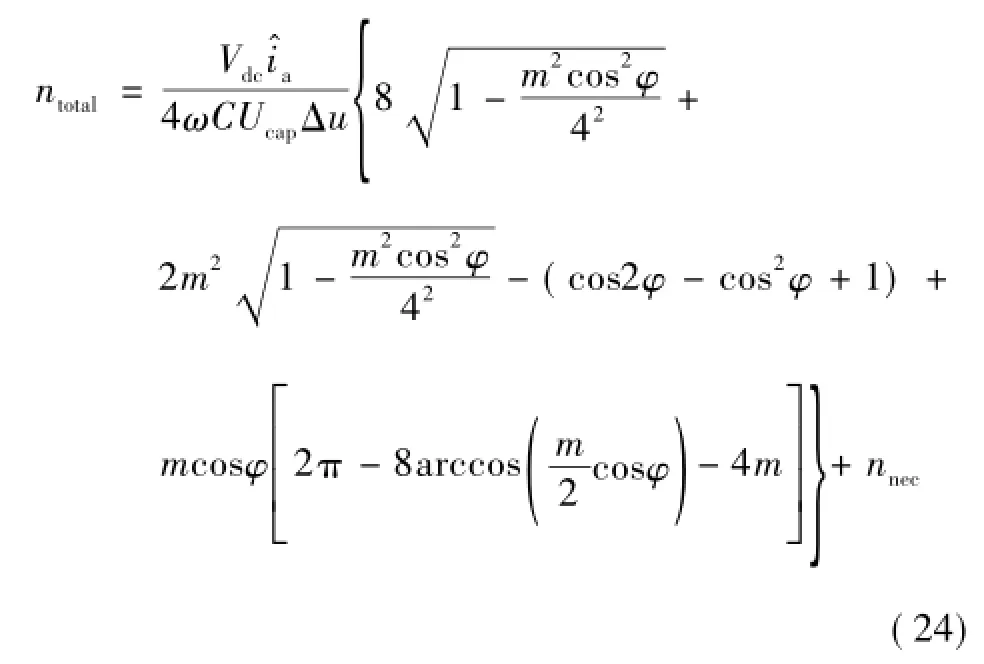
当MMC处于整流工作状态时，可分析出开关次数的结果与式（22）～式（24）一致。分析式（22）～式（24）可知MMC开关频率与子模块电容电压偏差呈反比，与MMC工作时的调制比和功率因数也呈递减的函数关系。其原因为:

1）因为电容电压偏差越大，子模块发生一次全交换的时间就越长，导致开关频率越小。

3）当功率因数越大，桥臂电流峰值处对应的调制波越接近其最大和最小值，即在交换时间最短处，其交换数量也越少，因此开关频率越小。

开关频率与电压差Δu、调制比m、功率因数角φ的关系如图5所示。

图5　开关频率变化趋势Fig.5　The trend graph of switching frequency

4　仿真验证

为验证改进均压算法在交流侧受到干扰时的有效性及本文所提出开关频率计算方法的正确性，本文利用Matlab对每个桥臂含有45个子模块的单相MMC逆变器进行了仿真分析，并与载波移相调制下均压算法在相同工况下进行了比较。系统仿真参数如表1所示。

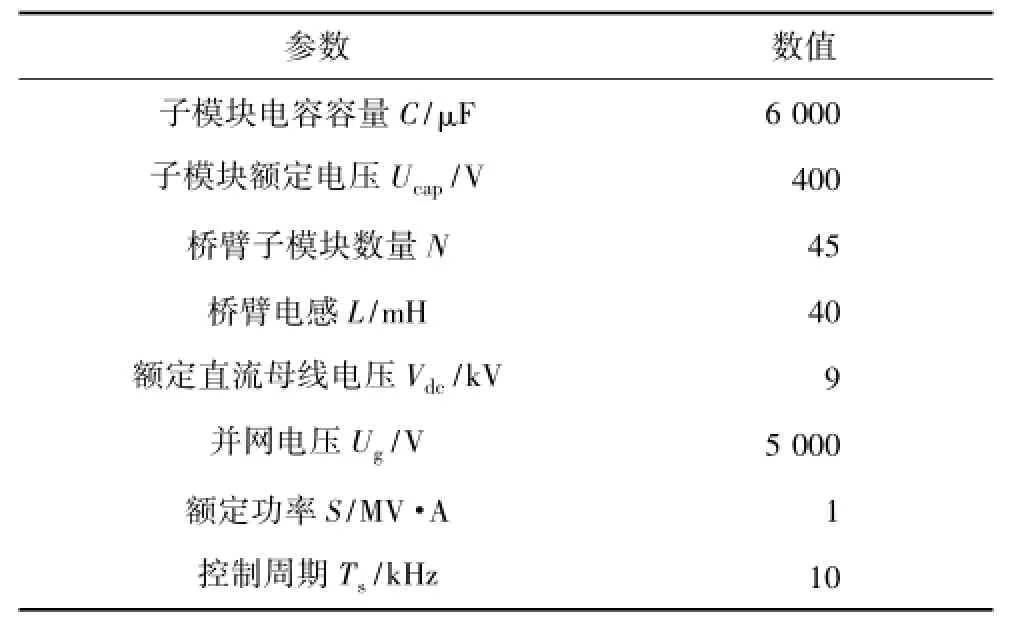
表1MMC仿真参数Tab.1　The parameters of MMC

首先对传统最近电平逼近均压控制方法进行电网故障时的仿真，逆变器输出0.5 MW的有功功率，在0.3 s时，电网电压下降50%，0.5 s后恢复到正常值，得到仿真结果如图6所示。图6a为电网电压和并网电流波形，图中电压和电流的基值分别设为5 000 V和200 A。图6b为上桥臂第一个子模块电容电压的波形，在电网电压正常时，电容电压波动约为30 V，电网故障后，子模块电压的波动增加近1倍。图6c为上桥臂每时刻最大电压偏差的波形，可看出其变化规律与式（10）一致，并且最大电压偏差不超过2.5 V。图6d为一个工频周期内，上桥臂所有子模块动作次数之和，从图中可看出在电网电压正常时，每个工频周期不超过3 750次，每个子模块的平均开关频率约为2 kHz，电网故障后每个子模块的平均开关频率约为3.45 kHz。

图6　传统均压方法的仿真波形Fig.6　Simulated wave of traditional voltage balance algorithm

然后在电网电压突变情况下对改进型均压方法和载波移相均压方法进行对比仿真，其中在改进型均压方法中，最大电压偏差取为4 V，此时平均开关频率约为450 Hz，载波移相均压算法开关频率与之相同，其他工况与传统方法一致。仿真结果如图7所示。图7a为上桥臂第一个子模块电容电压波形的对比，可看出采用改进的均压方法时电容电压波动比载波移相时稍大，但并不影响MMC的正常运行。图7b中，在相同开关频率下，采用载波移相均压算法时的最大电压偏差平均值比改进均压算法小，因为载波移相调制下的均压算法［18］在每个控制周期，每个子模块都会根据设定电压与实际电压偏差对每个子模块的调制波进行修正，所以每个子模块电压将会分布得更加均匀。在电网电压突增或突减时，改进均压算法最大电压偏差始终在设定值4 V上下波动。图7c为上桥臂所有子模块在每个工频周期内总开关次数，从图中可看出，采用基于最大电压偏差的优化均压方法后，在电网电压正常时，一个周期内的开关次数由3 750次降到约800次，此时单个子模块的开关频率约为445 Hz，基于载波移相调制的子模块开关频率不变。

图7　改进均压方法与载波移相均压算法的对比仿真波形Fig.7　Simulated wave with modified voltage balance algorithm and CPS-PWM

为了验证电压差与开关频率的关系，此时改变逆变器的工作方式，逆变器外接10 mH电感和50 Ω电阻串联，调制比取为1，此时的功率因数角为10.6°，负载电流为173 A，设电压差从1 V到8 V，每隔0.5 V变化一次进行仿真，仿真结果如图8所示。从图中可看出在电压差为1 V和1.5 V时，由于Δu＜Δu1，此时利用式（22）计算出的理论值与实际值误差较大。当Δu＞2 V后，理论值与实际值基本一致。

图8　开关次数与电压差变化Fig.8　Diagram of switching times changing with unbalance voltage

为了验证调制比与开关频率的关系，此时设电压偏差为2.5 V，逆变器外接506 μF的电容与桥臂的等效电感谐振后再与负载电阻串联，此时的功率因数角可近似为零，改变电阻的值，使在不同调制比时，保持负载电流峰值为174 A，得到的调制比与开关次数的关系如图9所示，可看出开关次数与调制比基本呈反比例关系，因为调制波接近Vdc/2时，每次交换的子模块数量最多。

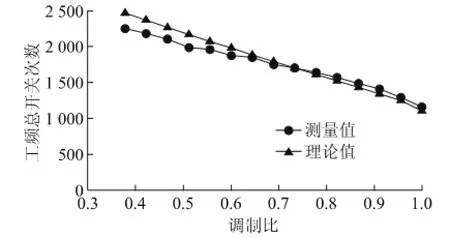
图9　开关次数随调制比的变化Fig.9　Digram of switching times changing with modulation rate

为了验证开关频率与负载的功率因数角的关系，设逆变器的调制比为1，电压偏差取为2.5 V。负载电流的峰值始终为180 A，改变外接负载的情况，使功率因数角在-90°到90°之间变化，仿真结果如图10所示，从图中可看出当逆变器工作在功率因数为1时开关频率最低，在功率因数为0时最大。

图10　开关次数随功率因数角的变化Fig.10　Digram of switching times changing with power factor angle

5　实验验证

本文搭建了九电平的MMC的单相实验平台，平台上下桥臂各8个子模块，子模块电容为450 V/6 800 μF，桥臂电感取为5.6 mH，IGBT采用SEMIKRON公司的SKM100GB12T4模块，驱动采用该公司的专用驱动核SKYPER 32 R，系统的脉冲输出采用 Altera公司的Cyclone II EP2C8Q208实现，每个子模块电容电压采样采用片外ADS8556实现。系统算法在TMS320F28335中完成。系统实物图如图11所示。

图11　单相九电平MMC实物图Fig.11　Laboratory prototype of nine level single phase MMC

九电平逆变器每个子模块的额定工作电压为50 V，调制比给定为0.9，逆变器外接11 Ω的电阻负载，图12为采用传统最近电平逼近法时逆变器的空载输出电压波形。图13为负载时MMC的输出电流和上下桥臂电流波形，输出电流中的谐波是由于MMC输出电平数较低产生的。图14为MMC工作时电容电压波形，电容电压测量是通过测量霍尔电压传感器的输出得到的，由于示波器通道的限制，只采样了上桥臂的4个子模块电容电压（10 mV对应0.264 V）。图15为子模块的脉冲波形，从图中可看出子模块在一个周期内的开关次数约为32次，开关频率约为800 Hz。

图12　MMC空载输出电压波形Fig.12　Experimental results of output voltage with no load

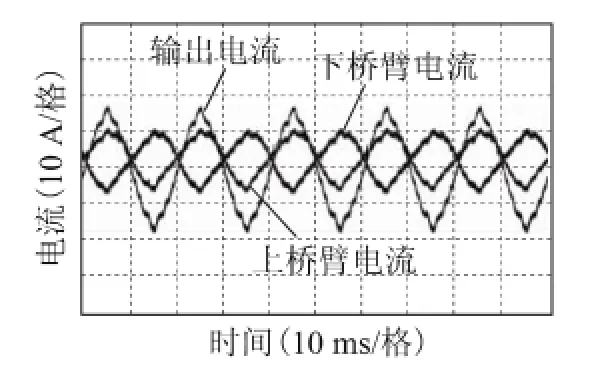
图13　输出电流及上下桥臂电流波形Fig.13　Experimental results of output current and arm current

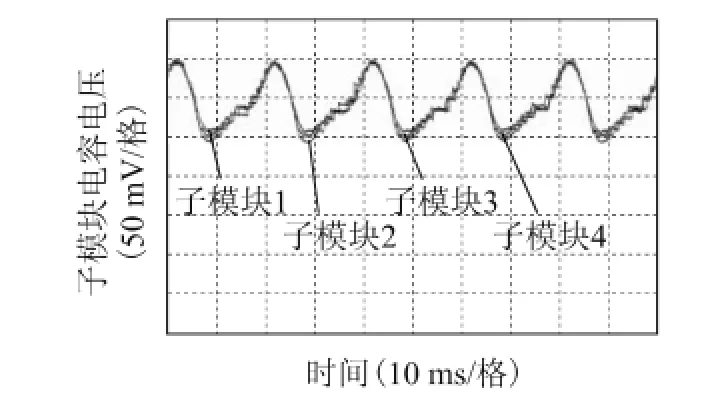
图14　电容电压波形Fig.14　Experimental results of capacitor voltage

图15　子模块的脉冲波形Fig.15　Experimental results of driver pluse

图16为采用改进型均压方法所得的上桥臂4路电容电压波形，此时电压差取为1.5 V，其他参数与传统方法的实验相同。从图16中可看出与传统均压方法相比，电容电压的一致性变差，但不会影响MMC的输出特性，因为从图17中可看出输出电流和上下桥臂电流波形与图13中的传统方法相比基本没有变化，但从图18可看出，在5个工频周期内子模块的开关次数约为25次，因此一个桥臂在一个工频周期内的开关次数为40次，开关频率约为125 Hz，与理论计算值42次基本一致。

图16　子模块的电容电压波形Fig.16　Experimental results of submodule capacitor voltage

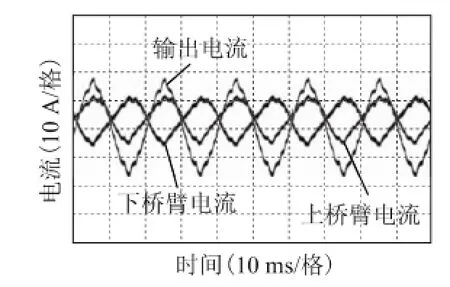
图17　输出电流与上下桥臂电流波形Fig.17　Experimental results of output current and arm current

6　结论

本文针对基于最大电压偏差的优化均压算法，在深入分析MMC开关过程的基础上，得到了采用基于最大电压偏差均压方法的平均开关频率解析表达式，总结出了开关频率与电压偏差、功率因数及调制比的关系，并给出了最大电压偏差的取值范围，为最大电压偏差的取值和MMC的开关损耗计算提供了理论参考，具有一定的实用价值。通过仿真和实验验证了改进均压方法的有效性和开关频率理论值的正确性。

［1］彭浩，邓焰，王莹，等.模块化多电平变换器模型及稳态特性研究［J］.电工技术学报，2015，30 （12）:120-127.

Peng Hao，Deng Yan，Wang Ying，et al.Research about the model and steady-state performance for modular multilevelconverter［J］.TransactionsofChina Electrotechnical Society，2015，30（12）:120-127.

［2］刘普，王跃，雷万钧，等.模块化多电平变流器稳态运行特性分析［J］.电工技术学报，2015，30 （11）:90-99.

Liu Pu，Wang Yue，Lei Wanjun，et al.Analysis of steady-state operating characteristics for modular multilevel converters［J］.Transactions of China Electrotechnical Society，2015，30（11）:90-99.

［3］Rohner S，Bernet S，Hiller M，et al.Modulation，losses，andsemiconductorrequirementsofmodular multilevel converters［J］.IEEE Transactions on Industrial Electronics，2010，57（8）:2633-2642.

［4］刘国伟，姜齐荣，魏应冬.低频率工况下模块化多电平变流器电容电压平衡控制策略［J］.电工技术学报，2014，29（8）:166-172.

Liu Guowei，Jiang Qirong，Wei Yingdong.Study on capacitor voltage balancing control of modular multilevel converters at low frequency［J］.Transactions of China Electrotechnical Society，2014，29（8）:166-172.

［5］张建坡，赵成勇.模块化多电平换流器环流及抑制策略研究［J］.电工技术学报，2013，28（10）: 328-336.

Zhang Jianpo，Zhao Chengyong.Research on circulation current and suppressing strategy of modular multilevel converter［J］.TransactionsofChinaElectrotechnical Society，2013，28（10）:328-336.

［6］高建，苏建徽，高航，等.模块化多电平换流器电容电压与环流的控制策略［J］.电力系统保护与控制，2014，42（3）:56-62.

Gao Jian，Su Jianhui，Gao Hang，et al.Capacitor voltage and circulation current control strategy in modular multilevel converter［J］.Power System Protection and Control，2014，42（3）:56-62.

［7］王琨，冯琳，李国杰.一种适用于飞跨电容型多电平逆变器的新型载波同相层叠PWM方法［J］.电力系统保护与控制，2014，42（14）:8-13.

Wang Kun，Feng Lin，Li Guojie.A novel carrier-based disposition PWM method with voltage balance for flying capacitor multilevel inverter［J］.Power System Protection and Control，2014，42（14）:8-13.

［8］王玉凤，张立，褚占军.载波调换调制技术在级联多电平SAPF中的应用［J］.电力系统保护与控制，2015，43（6）:14-18. Wang Yufeng，Zhang Li，Chu Zhanjun.Application of carrier exchange modulation technique in multi-level cascadedSAPF［J］.PowerSystemProtectionand Control，2015，43（6）:14-18.

［9］Meshram P M，Borghate V B.A simplified nearest level control（NLC）voltage balancing method for modular multilevel converter（MMC）［J］.IEEE Transactions on Power Electronics，2015，30（1）:450-462.

［10］Darus R，Pou J，Konstantinou G.A modified voltage balancing algorithm for the modular multilevel converter: evaluation for staircase and phase-disposition PWM［J］. IEEE Transactions on Power Electronics，2015，30（8）: 4119-4127.

［11］Lee H J，Jung J J，Sul S K.A switching frequency reduction and a mitigation of voltage fluctuation of modular multilevelconverterforHVDC［C］//IEEE Energy Conversion Congress and Exposition（ECCE），Pittsburgh，PA，2014:483-490.

［12］ 管敏渊，徐政.MMC型VSC-HVDC系统电容电压的优化平衡控制［J］.中国电机工程学报，2011，31 （12）:9-14.

Guan Minyuan，Xu Zheng.Optimized capacitor voltage balancing control for modular multilevel converter basedVSC-HVDCsystem［J］.ProceedingsoftheCSEE，2011，31（12）:9-14.

［13］屠卿瑞，徐政，郑翔，等.一种优化的模块化多电平换流器电压均衡控制方法［J］.电工技术学报，2011，26（5）:15-20.

Tu Qingrui，XuZheng，ZhengXiang，etal.An optimized voltage balancing method for modular multilevel converter［J］.TransactionsofChinaElectrotechnical Society，2011，26（5）:15-20.

［14］许烽，徐政，张哲任.基于降损调制技术的全桥MMC电容电压无需排序均衡控制［J］.电网技术，2013，37（12）:3347-3355.

Xu Feng，Xu Zheng，Zhang Zheren.Reduced loss modulation based capacitor voltage non-sorting balancing controlforfull-bridgeMMC［J］.PowerSystem Technology，2013，37（12）:3347-3355.

［15］Tu Qingrui，Xu Zheng.Impact of sampling frequency on harmonic distortion for modular multilevel converter ［J］.IEEE Transactions on Power Delivery，2011，26 （1）:290-306.

［16］Tu Qingrui，Xu Zheng.Reduced switching-frequency modulationandcirculatingcurrentsuppressionfor modular multilevel converters［J］.IEEE Transactions on Power Delivery，2011，26（3）:2009-2017.

［17］Chai R Z，Zhang B H，Hao Z G，et al.A low switching frequency voltage balancing strategy of modular multilevel converter［C］//TENCON IEEE Region 10 Conference，Xi'an，2013:1-4.

［18］ 赵昕，赵成勇，李广凯，等.采用载波移相技术的模块化多电平换流器电容电压平衡控制［J］.中国电机工程学报，2011，31（21）:48-55.

Zhao Xin，ZhaoChengyong，LiGuangkai，etal. Submodule capacitance voltage balancing of modular multilevel converter based on carrier phase shifted SPWM Technique［J］.Proceedings of the CSEE，2011，31 （21）:48-45.

黄守道男，1962年生，博士生导师，教授，研究方向为电力电子传动装置及其控制、新能源发电。

E-mail:hsd1962@hnu.edu.cn

高剑男，1979年生，讲师，研究方向为电力电子与电机控制技术。

E-mail:Gj_2520596@sina.com（通信作者）

Switching Frequency Analysis of Modular Multilevel Converter Based on the Improved Capacitor Voltage Balancing Algorithm

Huang ShoudaoLiao WuGao JianHuang ShengRong Fei
（College of Electrical and Information EngineeringHunan UniversityChangsha410082China）

This paper derives the analytical expressions of the modular multilevel converter（MMC）average switching frequency based on the inproved maximum sub-module voltage deviation，and analyzes the factors that affect the switching frequency.This paper can provide a theoretical guidance for the loss calculation and thermal design of MMC.The case studies are performed on a 46-level single-phase MMC under different operating conditions in Matlab/Simulink which proves the accuracy of this method.Meanwhile，a 9-level single-phase MMC laboratory prototype is built to verify the effectiveness of this method.

Modular multilevel converter，switching frequency，modified voltage balancing control，VSC-HVDC

TM464

国家国际科技合作专项项目（2011DFA62240）和国家自然科学基金项目（51377050）资助。

2015-03-24改稿日期 2015-06-10