RBCC高超声速巡航飞行器轨迹优化与设计

郑 雄 刘竹生 杨 勇 姚世东 陈洪波

1.中国运载火箭技术研究院研究发展中心，北京 100076 2.中国运载火箭技术研究院，北京 100076



RBCC高超声速巡航飞行器轨迹优化与设计

郑 雄1刘竹生2杨 勇1姚世东1陈洪波1

1.中国运载火箭技术研究院研究发展中心，北京 100076 2.中国运载火箭技术研究院，北京 100076

巡航飞行器正向着快速响应、高超声速巡航和强突防的方向发展，火箭基组合循环(Rocket Based Combined Cycle, RBCC)推进系统是此类飞行器的潜在动力。本文以RBCC高超声速巡航飞行器为研究对象，对其飞行任务剖面进行规划与分析，并针对其轨迹优化设计问题，采取分段求解的思路：分别建立飞行器爬升段和巡航段轨迹设计数学模型，在此基础上，应用粒子群优化(Particle Swarm Optimization, PSO)算法对爬升段轨迹进行优化设计，而对于巡航段轨迹，则采用数值方法求解，两段轨迹求解过程中均考虑飞行动压、过载的约束以及控制变量的取值范围限制。仿真结果表明，所得到的轨迹满足飞行任务剖面需求及动压、过载等约束，验证了所用方法的有效性。

RBCC；高超声速巡航飞行器；粒子群优化算法；轨迹优化

火箭基组合循环(Rocket Based Combined Cycle, RBCC)发动机将火箭发动机和冲压发动机有机结合在一个流道中，能充分发挥火箭发动机大推重比和冲压发动机高比冲的优点，是高超声速巡航飞行器及可重复使用运载器最理想的动力装置之一。目前，国内外学者对RBCC可重复使用运载器上升段轨迹设计进行了大量研究，得到了一些有益的结论[1]，而对RBCC高超声速巡航飞行器的轨迹设计研究较少。王厚庆等人[2]通过求解纵向平面内的质点运动方程，对RBCC巡航飞行器的爬升段飞行轨迹和有效载荷能力进行了分析，但没有采用优化方法，无法获得性能最优的飞行轨迹。吕翔等人[3]给出了基于马赫数-动压参考曲线的RBCC巡航飞行器爬升段轨迹设计方法，同样没有采用优化方法，未求得最优解。李响等人[4]利用遗传算法对RBCC高超声速导弹的爬升和巡航段航程进行优化设计，但在轨迹优化设计的过程中未考虑动压、过载等约束，所得结果可能出现不可行点。

本文以RBCC高超声速巡航飞行器为研究对象，首先对其飞行任务剖面进行规划与分析；然后建立用于飞行器轨迹设计的数学模型；最后基于该模型应用粒子群优化算法对爬升段轨迹进行优化设计，并采用数值方法求解飞行器巡航段轨迹。旨在为RBCC高超声速巡航飞行器的轨迹优化设计提供一种可行途径。

1 飞行任务剖面

根据RBCC发动机多模态、高比冲的优势以及目前其引射模态推力不够的现状，本文设计RBCC高超声速巡航飞行器任务剖面如图1所示。组合体飞行器由载机水平投放，5s后，固体火箭助推器点火，飞行器加速爬升至18km高空，马赫数达到4.5。此时固体火箭助推器耗尽关机，巡航飞行器与助推器分离，RBCC发动机启动。经过亚燃冲压模态和超燃冲压模态，巡航飞行器爬升到高度28.5km，马赫数达到6.5，飞行器转入等高等速巡航段。当临近目标上空时，飞行器下压俯冲，对目标进行攻顶打击。

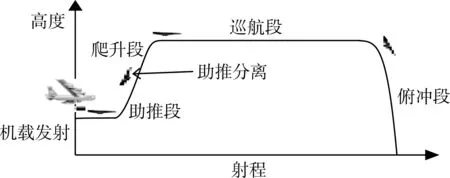
图1 RBCC高超声速巡航飞行器任务剖面

根据以上任务剖面，可将RBCC高超声速巡航飞行器飞行轨迹分为助推段、爬升段、巡航段和俯冲段。为简化设计，暂不考虑助推段和俯冲段，只研究RBCC高超声速巡航飞行器的爬升段和巡航段。

2 数学模型

2.1 飞行轨迹计算模型

将飞行器视为可控质点，在不考虑风及假设地球为平面大地且忽略自转的情况下，飞行器在纵向平面内的运动方程如下：

(1)

(2)

式中，g0为海平面重力加速度，取9.8066m/s2；R0为地球半径，取6356.766km。

在巡航段，飞行器处于等高等速平飞状态，其轨迹倾角θ=0°，受力关系需满足：

(3)

2.2 气动力模型

飞行器所受的升力和阻力分别由式(4)和(5)确定：

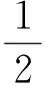
(4)

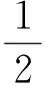
(5)

式中，CL，CD分别为飞行器升力系数和阻力系数，ρ为大气密度，S为飞行器参考面积。本文气动外形采用X-43A的乘波体外形，文献[5]以表格形式给出了X-43A的气动性能结果。

2.3 推力模型

SCCREAM(SimulatedCombinedCycleRocketEngineAnalysisModule)是国际上使用较广的RBCC发动机性能计算平台，本文采用文献[6]中由SCCREAM计算得到的RBCC发动机比冲性能，该发动机以液氢、液氧为燃料。根据发动机比冲和推进剂质量秒流量即可求出推力，计算公式如下：

(6)

2.4 大气模型

本文采用USSA-1976标准大气模型，具体计算公式参见文献[7]。

2.5 约束模型

2.5.1 动压约束

动压一方面为飞行器提供升力和阻力，另一方面还为姿态控制提供操纵力矩，但是如果动压过大，飞行器的机械结构将受到影响，还会导致舵机因铰链力矩太大而不能有效工作，影响飞行器的姿态控制。因此必须对动压进行限制，如下式：

(7)

其中，Pdmax为最大允许动压。

2.5.2 过载约束

高超声速飞行器的结构强度是一定的，为保证其在执行飞行任务过程中结构的安全，需要对飞行器的过载进行限制，如下式所示：

(8)

其中，nx和ny分别为飞行器切向过载和法向过载，nmax为最大允许过载。

2.5.3 末端状态约束

根据飞行任务剖面，要求爬升段的末端状态达到期望的等高等速平飞状态，因此其末端约束如下：

(9)

其中，下标“f”表示爬升段末端，上标“*”表示期望。

2.5.4 控制量约束

为满足RBCC发动机的吸气条件，飞行器攻角必须满足一定的边界约束条件。此外，为保证燃烧过程充分、稳定，发动机推进剂质量秒流量也有一定的范围。因此控制量约束如下所示：

(10)

3 粒子群优化算法

3.1 粒子群优化算法原理[8-9]

设PSO算法中有N个粒子，每个粒子k(k=1,2,…,N)表示优化问题解空间中的一个备选解，所有粒子都有自己的位置x(k)=[x1(k),x2(k),…,xn(k)]T(n为待优化变量的个数)，速度v(k)=[v1(k),v2(k),…,vn(k)]T，以及1个由目标函数J决定的适应度，比较各粒子目标函数的值可判断粒子的优劣。根据每个优化变量的取值范围xi∈[ai,bi](其中，i=1,2,…,n)，对粒子位置和速度的限制为：

(11)

(12)

式中，ω为惯性权重系数，c1为粒子跟踪自身历史最优值的权重系数，c2为粒子跟踪群体最优值的权重系数，r1，r2为[0,1]内的随机数。

3.2 粒子群优化算法应用

应用PSO优化算法对RBCC高超声速巡航飞行器爬升段轨迹进行优化时，需要完成以下3个方面的工作。

(1)目标函数的确定

高超声速巡航飞行器的射程主要与可用燃料有关，在爬升段节省燃料具有重要的意义，因此本文选择燃料最省作为轨迹优化的性能指标，也即要求爬升段末端飞行器质量最大，目标函数取为J=max(mf)。

(2)控制变量的参数化

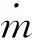
(3)约束的处理

对于等式约束式(9)，可采用在目标函数上添加惩罚项来解决，此方法为罚函数法，具体公式如下：

(13)

式中，J′为新的目标函数，ζ1，ζ2，ζ3为惩罚因子，其取值依赖于经验。

若任一粒子k违背了不等式(7)或(8)，则令其J′(k)=-∞，v(k)=0，如此相当于减小了控制变量的搜索空间，以满足飞行器轨迹的不等式约束。

综上，可得PSO优化算法应用于RBCC高超声速巡航飞行器爬升段轨迹优化的流程如图2所示。

图2 巡航飞行器爬升段轨迹优化设计流程

4 仿真算例

4.1 仿真条件

基于上文规划的飞行任务剖面，RBCC高超声速巡航飞行器的爬升段始于高度18km，4.5Ma，并于高度28.5km，6.5Ma处转入等高等速巡航状态。巡航飞行器初始质量为1500kg，初始轨迹倾角为5°，射程2000km。飞行过程中，攻角取值范围为-4°～8°，推进剂质量秒流量取值范围为0.1～1kg/s，全程要求动压不大于110kpa，切向过载和法向过载的绝对值均不大于2。RBCC发动机在6Ma时由亚燃冲压模态转入超燃冲压模态。粒子群优化算法参数为：N=100，NIT=120，ω=0.729，c1=c2=2。

4.2 仿真结果

图3给出了巡航飞行器在爬升段的飞行性能。其中，图(a)是飞行器的飞行轨迹及轨迹倾角变化曲线，固体火箭助推器分离后，飞行器继续爬升到巡航高度28.5km，同时轨迹倾角先减小、后增大、最后逐渐减小为-0.000075°；图(b)为飞行器飞行动压及马赫数随时间的变化曲线，随着飞行器的爬高动压逐渐减小，在75s以后，由于飞行轨迹趋于水平，高度增加缓慢，而速度仍然保持较快增长，故动压稍有增大，整个爬升段，动压都不大于110kpa，爬升段末端马赫数为6.485；图(c)为飞行速度及飞行器质量随时间的变化曲线，爬升段末端飞行速度为1950m/s，飞行器质量为1444kg；图(d)为攻角和推进剂质量秒流量曲线，由图可知，爬升段控制变量曲线在约束范围内，且变化平缓、光滑，便于飞行器控制；图(e)为飞行器法向过载和切向过载的变化曲线，其全程绝对值均不大于2，图中切向过载于61s处发生突变，这是因为RBCC发动机由亚燃冲压模态转为超燃冲压模态比冲大幅减小导致，此时，因为攻角较小，所以对法向过载的影响有限；图(f)为PSO优化算法中目标函数值随迭代次数的变化曲线，由图可知，粒子群在经过40次迭代后即可找到次优解，因此在迭代次数和解的优劣之间存在一个折衷，本文为寻得最优解，在迭代次数的选择上较保守。

图4给出了巡航飞行器爬升段和巡航段的仿真结果。可知，飞行器能顺利由爬升段转入巡航段，全程飞行耗时1041s，射程2000km，推进剂消耗量为282kg，占巡航飞行器总质量的18.8%，这为飞行器的结构质量和有效载荷质量留下很大的空间，推进剂质量秒流量最大值和最小值分别为0.6571kg/s，0.2322kg/s，调节比为2.8299。整个飞行过程中，动压、过载及控制量取值均在要求范围内。需要特别说明的是，由于巡航段采用数值方法求解攻角和推进剂质量秒流量，受精度限制，飞行过程中法向过载和切向过载分别不严格等于1和0，这从图4 (e)可以看出，小量的积分将导致速度缓慢增加，以及轨迹倾角在0°附近波动，从而引起飞行高度的波动，最大波动幅度为330m，随着时间的推移，积分会逐渐消除误差，因此，轨迹倾角、飞行高度的波动越来越小，马赫数也趋于稳定。

图3 RBCC高超声速巡航飞行器爬升段飞行性能

5 结论

针对RBCC高超声速巡航飞行器的轨迹优化设计问题，基于规划的飞行任务剖面，采取分段求解的思路，即应用PSO算法对爬升段轨迹进行优化设计，

而对于巡航段轨迹，则采用数值方法求解。两段轨迹求解过程均考虑飞行动压、过载的约束以及控制变量的取值范围限制。数值仿真验证了所用方法的有效性，结果可为RBCC高超声速巡航飞行器的任务规划及轨迹优化设计提供参考。

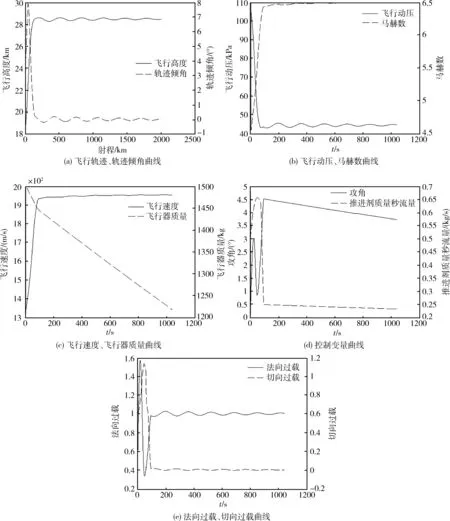
图4 RBCC高超声速巡航飞行器爬升段、巡航段飞行性能

[1]KoderaM,OgawaH,TomiokaS,etal.Mult-ObjectiveDesignandTrajectoryOptimizationofSpaceTransportSystemswithRBCCPropulsionviaEvolutionaryAlgorithmsandPseudospectralMethods[R].AIAA2014-0629, 2014.

[2] 王厚庆, 何国强, 刘佩进, 吕翔. 以RBCC为动力的巡航飞行器轨迹与质量分析[J]. 西北工业大学学报, 2006, 24(6): 774-777.(WangHouqing,HeGuoqiang,LiuPeijin,LvXiang.AnalysisofTrajectoryandMassforRBCC-PoweredCruiseVehicle[J].JournalofNorthwesternPolytechnicalUniversity, 2006, 24(6): 774-777.)

[3] 吕翔, 何国强, 刘佩进.RBCC飞行器爬升段轨迹设计方法[J]. 航空学报, 2010, 31(7): 1331-1337.(LvXiang,HeGuoqiang,LiuPeijin.AscentTrajectoryDesignMethodforRBCC-poweredVehicle[J].ActaAeronauticaEtAstronauticaSinica, 2010, 31(7): 1331-1337.)[4] 李响, 柳长安, 王泽江, 张后军. 对某吸气式高超声速导弹的航程优化与分析[J]. 兵工学报, 2012, 33(3): 290-294.(Li Xiang, Liu Changan, Wang Zejiang, Zhang Houjun. Trajectory Optimization for Maximizing Cruise Range of Air-breathing Hypersonic Missile[J]. Acta Armamentarii, 2012, 33(3): 290-294.)

[5] Brock M A. Performance Study of Two-stage-to-orbit Reusable Launch Vehicle Propulsion Alternatives[D]. Ohio: Air Force Institute of Technology, 2004.

[6] Olds J R, Ledsinger L, Bradford J, et al. Stargazer: A TSTO Bantam-X Vehicle Concept Utilizing Rocket-Based Combined Cycle Propulsion[J]. AIAA Paper, 1999: 99-4888.

[7] 杨炳尉. 标准大气参数的公式表达[J]. 宇航学报, 1983, 4(1): 83-86.(Yang Bingwei. Formulization of Standard Atmospheric Parameters[J]. Journal of Astronautics, 1983, 4(1): 83-86.)

[8] Eberhart R C, Kennedy J. A New Optimizer Using Particle Swarm theory[C]. Proceedings of the Sixth International Symposium on Micromachine and Human Science, 1995, 1: 39-43.

[9] Shi Y, Eberhart R C. A Modified Particle Swarm Optimizer[C]. Proceedings of the IEEE World Congress on Computational Intelligence, 1998: 69-73.

[10] 龚春林, 韩璐, 谷良贤. 适应于RBCC运载器的轨迹优化建模研究[J]. 宇航学报, 2013, 34(12): 1592-1598.(Gong Chunlin, Han Lu, Gu Liangxian. Research on Modeling of Trajectory Optimization for RBCC-Powered RLV[J]. Journal of Astronautics, 2013, 34(12): 1592-1598.)

征稿简则

1.文稿应具备创新性和科学性，务求主题突出、论据充分、文字精练、数据可靠，有较高的理论水平和实用价值。

2.稿件的篇幅(含摘要、图、表、参考文献等)6000字以内，撰写论文所涉及的基金资助项目、获奖课题内容请予注明。

3.文章中必须有中英文的题名、作者姓名、单位(对外名称)、邮编、摘要、主题词，还应有中图分类号和参考文献。其中中文题名不超过20个字，英文题名不超过12个实词。主题词3条～8条，注意使用规范词。

4.摘要采用报道性文摘，应拥有与论文同等量的主要信息，着重反映新内容。中英文摘要均须包括目的、方法、结果、结论等四要素，中文摘要以300字左右为宜。英文摘要应按照英文文法书写，在确保内容完整性的前提下不必采用句子到句子的翻译模式。

5.计量单位应使用国家最新颁布的国家标准和规定，并且一律用符号表示。

6.稿件中的插图、表格要少而精。构图要合理，应附有图表序号及中文的图题、表题及图表注释。

7.参考文献采用中英双语著录，应著录最必要、最新的文献，且应是国内外公开发表的书刊文章，编号以出现的先后为序，各类文献的著录格式为：

(1)专著：著者.书名[M].版本(第1版不用著录).出版地：出版者，出版年.

(2)期刊：作者．题名[J]．刊名，年，卷(期)：起止页码.

(3)论文集：作者.题名[C]//编者.文集名.出版地：出版者，出版年：起止页码.

(4)学位论文：作者.题名[D].保存者，年份.

(5)会议论文：作者.题名[C].会议名称，会址，会议年份.

(6)技术标准：责任者.标准代号 标准名称[S].出版地：出版者，出版年：引文页码.

(7)专利文献：专利申请者.专利题名：专利国别，专利号[P].公开日期.

(8)报纸：作者.题名[N].报纸名，年-月-日(版次).

(9)外文文献请注意作者的名字均为姓在前名在后，名要缩写。

例：Zhou K M, Doyle J C, Glover K. Robust and Optimal Control[M]. Upper Saddle River, New Jersey: Prentice-Hall, 1996.

8.来稿须经过保密审查，勿投寄涉密稿件。稿件请注明作者真实姓名(发表时可按作者意愿署名)、工作单位、详细通讯地址、邮政编码、电话、作者简介及第一作者照片，文稿一经刊载即酌致稿酬，并赠送期刊2份。未被录用的稿件恕不退稿。

9.请勿一稿多投，凡在6个月内未见编辑部稿件处理的通知，请与编辑部联系。已在公开刊物发表的论文和报告，本刊不再刊登。

10.投稿方式：网上投稿，网址为http://htkz.cn；请同时邮寄保密审查结论至编辑部。来稿须保证内容真实、未侵犯他人知识产权、无涉密内容，作者署名无争议，未一稿多投。稿件请用WORD格式。

Trajectory Optimization and Design for RBCC Hypersonic Cruise Vehicle

Zheng Xiong1, Liu Zhusheng2, Yang Yong1, Yao Shidong1, Chen Hongbo1

1.China Academy of Launch Vehicle Technology R&D Center, Beijing 100076, China 2.China Academy of Launch Vehicle Technology, Beijing 100076, China

Cruisevehicleisheadingtothedevelopmentofrapidresponse,hypersoniccruiseandstrongpenetrationandrocketbasedcombinedcyclepropulsionsystemisthepotentialpowerofsuchkindofaircraft. RBCChypersoniccruisevehicle,planningandanalyzingitsmissionprofilearefocusedinthispaper.Regardingthetrajectoryoptimization,sub-solvingideaisadopted:establishingmathematicalmodelsofaircraftclimbandcruiseperiodsseparately;Applyingparticleswarmoptimizationalgorithmtotrajectoryoptimizationoftheclimbbasedonmodelsabove;Usingnumericalmethodsduringthecruise.Duringthetwotrajectorydesignprocesses,constraintsofflightdynamicpressure,overloadandcontrolvariablesareconsidered.Thesimulationresultsshowthatthemissionprofilerequirementsanddynamicpressure,overloadandotherconstraintsarefulfilledintheobtainedtrajectoryandtheeffectivenessofthemethodisverified.

RBCC;Hypersoniccruisevehicle;Particleswarmoptimizationalgorithm;Trajectoryoptimization

2016-02-03

郑 雄(1989-)，男，湖北人，博士研究生，主要研究方向为飞行器总体设计；刘竹生(1939-)，男，黑龙江人，院士，博士生导师，主要研究方向为火箭与导弹总体设计；杨 勇(1968-)，男，四川人，博士，研究员，主要研究方向为飞行器总体设计；姚世东(1962-)，男，北京人，硕士，研究员，主要研究方向为结构机构总体设计；陈洪波(1978-)，男，天津人，博士，研究员，主要研究方向为飞行器总体设计。

V421.1

A

1006-3242(2016)05-0021-06