最优奇偶向量法在冗余捷联惯组故障检测中的应用研究

李超兵 张志良

北京航天自动控制研究所， 北京100854



最优奇偶向量法在冗余捷联惯组故障检测中的应用研究

李超兵 张志良

北京航天自动控制研究所， 北京100854

验证了最优奇偶向量法(OPT)在3套正交安装的捷联惯组下故障检测的可行性及其检测效果。针对2种不同的故障模型(硬故障和缓变故障)，分别进行了仿真试验，证明最优奇偶向量法对硬故障检测的灵敏度很高，但对于缓变故障，检测存在一定的延迟。与阈值法相比，最优奇偶向量法的检测效果总体较优，在中等幅值故障(2～4(°)/h)的检测上，漏警率至少降低1个数量级。 关键词 故障检测; 最优奇偶向量法(OPT); 捷联惯组; 冗余配置

在现代航空航天事业中，导航系统的精度和可靠性显得越来越重要。故障检测与诊断技术为提高系统的可靠性提供了一条有效途径。在捷联惯导系统(SINS)中，惯性组件是导航与控制系统的关键部件，通常是控制系统中容易发生故障的部分并易受不良环境的影响，而且由于它们的体积和重量都较小，因此多采用传感器级的余度配置来提高系统的可靠性[1]。对冗余传感器实现故障检测、诊断与隔离和系统重构，使导航系统具有容错能力。在火箭的故障检测系统中，惯性测量装置系统级冗余是根据获得的三惯组输出量，从整个控制系统角度，进行典型故障阈值的设计，通过故障的判别和表决，输出诊断后的正确结果，从而计算火箭的导航信息[2]。

国内外对最优奇偶向量法在冗余捷联惯组故障检测中的应用也有深入的研究。李延龙[3]针对冗余配置惯导系统的渐变型故障，提出了奇偶方程残差品质的概念以及模糊评估方法，并应用残差品质构成最小二乘加权阵，设计冗余配置的捷联惯组智能自适应渐变型故障容错方法。金宏[4]等介绍了基于奇偶空间结构的奇偶向量的定义方法，并描述了其在传感器误差检测与隔离中的应用。Steven Ray Hall[5]介绍了故障检测与隔离算法中的奇偶向量定义，并提出采用滤波方法来补偿由于漂移、刻度系数误差和安装误差所引起的奇偶向量误差，从而对捷联惯组误差进行建模和分析。梁海波等[6]将支持向量机和最优奇偶向量法相结合，将冗余陀螺测量单元中所有陀螺的奇偶残差看做整体，作为多故障支持向量分类机进行训练数据，并从训练数据预处理核函数选择和参数寻优等方面进行了研究。田露等[7]针对陀螺漂移增大这种渐变故障，提出了一种UKF结合姿态运动学方程进行角速率估计，从而进行陀螺故障预报的方法。

对采用3套正交惯组配置(见图1)的捷联惯组，通常用阈值比较法进行故障检测，本文研究采用最优奇偶向量法进行故障检测，并分析最优奇偶向量法特点。

1 基于最优奇偶向量法的故障检测

1.1 冗余捷联惯组

本文研究的冗余捷联惯组为三捷联惯组系统，安装方式见图1。由3套相同的捷联惯组(AxAyAz，BxByBz和CxCyCz)同轴同向安装，每套惯组都是常规的三正交安装体系，可以认为是3个正交轴(x轴，y轴，z轴)上都安装了3个相同的传感器。

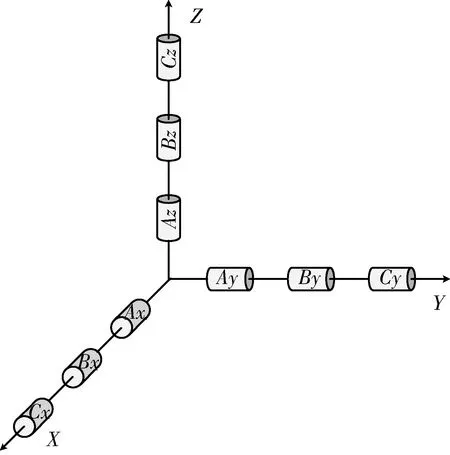
图1 三捷联配置方式

三捷联配置方式的测量矩阵为：

1.2 最优奇偶向量法

对于一般的测量方程[4]：

Z=HX+Df+Fε

(1)

其中，Z是惯组测量结果；H是陀螺仪或加速度计的安装矩阵，H∈Rm×3，m是惯性传感器的个数；X是载体运动状态；D是故障输入矩阵；f是故障向量；F是噪声输入矩阵；ε是随机噪声；D和F在简化模型中可取为单位阵。

由奇偶向量的性质和式(1)可得m个奇偶方程

(2)

设已检测出系统发生了故障，则按如下决策进行故障隔离，若

(3)

则判断第i个传感器发生故障。

不失一般性，考虑第i个故障发生，其他m-1个故障未发生的情况，奇偶方程化为[4]

(4)

(5)

为设计对第i个传感器故障敏感的最优奇偶向量vi，建立性能指标函数[7]

(6)

由几何安装矩阵H得相应的最优奇偶矩阵

2 故障模型

本文主要研究2种故障形式：硬故障和缓变故障。

硬故障是惯组输出发生大幅值的跳变，而缓变故障则是惯组输出附加上1个随时间增加而逐渐积累的小幅值故障。

仿真试验中利用阶跃信号模拟硬故障，用斜坡信号模拟缓变故障。

故障注入是在正常输出信号的基础上附加故障信号。

fi(t)=zi(t)+bi(t)

(7)

式中，zi为第i个陀螺(或加速度计)的输出值，bi为故障信号，fi是含故障的惯组输出。

硬故障模型：

(8)

式中，δ为故障幅值，t0为故障发生时刻。

缓变故障模型：

(9)

式中，t0为故障发生时刻，k为缓变故障的斜率。

3 仿真试验

采用实测飞行数据作为惯组所测量的飞行器真实状态，在此基础上，加入测量误差、噪声和故障来模拟真实的三捷联惯组输出，试验流程图如图2。

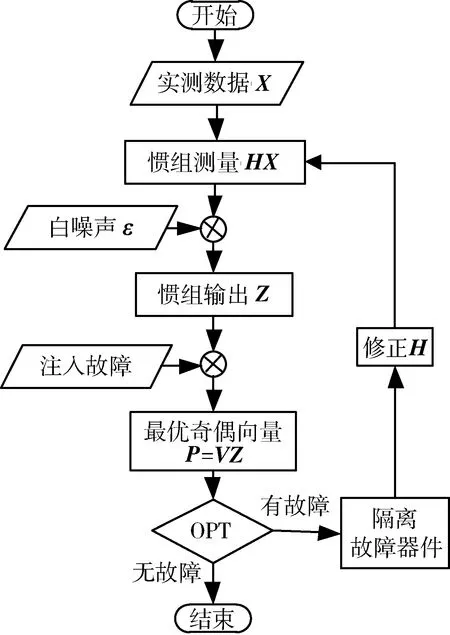
图2 仿真试验流程图

3.1 硬故障检测效果

选取一条60s的标准飞行弹道，在30s处给第8号陀螺加入10(°)/h幅值的硬故障，见图3。

图3 硬故障的OPT检测效果

为了减小野点的干扰，本文采取连续检测5拍数据的方法来排除：连续5拍数据都超过阈值，则认为发生故障。仿真结果见表1。

3.2 缓变故障检测效果

同样在选定的60s标准弹道上30s处注入斜率为1(°)/h≈5×10-6缓变故障，见图4。

表1 5000次蒙特卡洛打靶结果

图4 缓变故障的OPT法检测效果

在对缓变故障进行检测时，同样采用蒙特卡洛打靶法试验，表2为5000次蒙特卡洛打靶的结果。

由表2可以看出，幅值越小的缓变故障，检测延迟越大，每一种情况大致满足：

故障斜率×平均延迟≈常值。

这说明，OPT法对于缓变故障要等到缓变积累达到阈值之上才能检测到。

表2 5000次蒙特卡洛打靶结果

3.3 故障检测效果对比

对于图1所示的三捷联安装方式，经典的故障检测方法是阈值比较法，比较同轴向3个传感器的输出结果，两两做差，若差值超出阈值，则认为出现故障，最不一致的传感器即为故障传感器。

表3 5000次蒙特卡洛打靶结果

对比表1和表3的仿真结果，可以看出：1)对于幅值为1(°)/h及以下的故障，2种方法的检测效果都很差；2)对于幅值为2～4(°)/h的故障，最优奇偶向量法的检测效果较好；3)对于幅值为5(°)/h及以上的故障，2种方法的检测效果都很好。

总体上来看，最优奇偶向量法的检测效果好于阈值比较法。

4 结论

研究了最优奇偶向量法在特定配置——三捷联配置下的适用性，可知最优奇偶向量法可以应用到成套冗余的捷联惯组的故障检测上，拓宽了最优奇偶向量法的应用范围，不止是采用斜置冗余的配置方式。

最后，利用仿真试验研究了最优奇偶向量法对硬故障和缓变故障的检测效果，最优奇偶向量法的检测效果好于经典的阈值比较法，却不能从根本上解决缓变故障检测延迟大的问题。

[1] 中国科学技术协会.航天科学技术学科发展报告(2012-2013)[M].北京:中国科学技术出版社, 2014.(China Association for Science and Technology. Report on Advances in Space Science and Technology (2012-2013)[M]. Beijing: Science and Technology of China press, 2014 .)

[2] 李学峰, 王青, 王辉，等. 运载火箭飞行控制系统设计与验证[M].北京:国防工业出版社, 2013.(Li Xuefeng, Wang Qing, Wang Hui, et al. Design and Verification for Flight Control System of Launch Vechile[M]. Beijing: National Defense Industry Press, 2013.)

[3] 李延龙, 吴训忠. 一种冗余配置的惯性导航系统渐变型故障容错方法[J].弹箭与制导学报, 2008, 28(2): 57-60.(Li Yanlong,Wu Xunzhong.Gradual Fault-tolerance Design of Redundant SINS[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(2): 57-60.)

[4] 金宏, 张洪钺, 金忠.对特定传感器故障敏感的最优奇偶向量隔离与隔离方法[J].航空学报, 1997, 18(4):385-387.(Jin Hong, Zhang Hongyue. Fault Detection and Isolation Using Optimal Parity Vector Sensitive to Special Sensor Fault[J]. Acta Aeronautica et Astronautica Sinica, 1997, 18(4):385-387.)

[5] Hall S R. Parity Vector Compensation for FDI[D]. Aeronautics and Astronautics, 1981.

[6] 梁海波, 许昊, 吕章刚.基于支持向量机的冗余陀螺故障诊断方法[J]. 航天控制, 2014, 32(5): 77-83.(Liang Haibo, Xu Hao, Lv Zhanggang, et al. The Fault Diagnosis Method of Redundant Gyroscopes Based on Support Vector Machine[J]. Aerospace Control, 2014, 32(5): 77-83.)

[7] 田露, 董云峰.基于UKF的陀螺故障预报方法[J]. 航天控制, 2014, 32(3): 76-80.(Tian Lu, Dong Yunfeng. Gyro Fault Prediction Algorithm Based on UKF[J]. Aerospace Control, 2014, 32(3): 76-80.)

[8] 秦永元, 张洪钺, 汪叔华.卡尔曼滤波与组合导航原理[M].第二版. 西安: 西北工业大学出版社, 2012.(Qin Yongyuan, Zhang Hongyue, Wang Shuhua. Kalman Filter and Integrated Navigation Theory[M]. Second Edition. Xi’an: Northwestern Polytechnical University press, 2012.)

[9] Jin Hong, Zhang Hong Yue. Optimal Parity Vector Sensitive to Designated Sensor Fault[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(4): 1122-1128.

Optimal Parity Vector Technology Applied to Fault Detection of Redundant Inertial Measurement Unit

Li Chaobing, Zhang Zhiliang

Beijing Aerospace Automatic Control Institute，Beijing 100854，China

Thefeasibilityandthefaultdetectioneffectareverifiedbyoptimalparityvectortechnology(OPT)inthreeorthogonallyIMU.Accordingtodifferentfaultmodels,thesimulationtestsareimplemented.Itisproventhathardfaultcanbedetectedsensitivelybytheoptimalparityvectortechnology.Butforsofthard,thereiscertaindelayremaining.ThesimulationresultsshowthatOPThasbetterresultsthanthresholdcomparisonmethod.TheOPTmethodcandecreasesprobabilityofmissalarm(PMA)byoneorderofmagnitudeduringdetectingmiddlemagnitudefaultof2～4(°)/h.

Faultdetection;Optimalparityvectortechnology(OPT);Inertialmeasurementunit;Redundantconfiguration

2014-10-11

李超兵(1981-)，男，湖南娄底人，高级工程师，主要研究方向为导航、制导与控制；张志良(1982-)，男，辽宁营口人，工程师，主要研究方向为导航、制导与控制。

V249

A

1006-3242(2016)02-0086-05