高超声速飞行器全方位俯冲制导方法

申连杰 刘鲁华 汤国建 朱建文

国防科学技术大学，长沙 410073



高超声速飞行器全方位俯冲制导方法

申连杰 刘鲁华 汤国建 朱建文

国防科学技术大学，长沙 410073

针对高超声速飞行器俯冲段全方位攻击问题，为满足落点、速度倾角及入射方位角约束，以能量损耗最小为性能指标推导出全方位攻击最优制导律；进一步利用对称原理获得全方位俯冲制导策略，以避免在某些情况下的能量过度消耗。以CAV-H为例进行了仿真分析，结果表明该方法能高精度地满足终端多种约束，并实现全方位攻击，可为高超声速飞行器俯冲段精确制导提供参考。 关键词 高超声速飞行器；俯冲制导；全方位；多约束

高超声速飞行器是指飞行在临近空间并且飞行马赫数大于5的飞行器，该飞行器在机动性、突防能力、射程以及打击精度等方面具有显著优势，是实现全球快速精确打击的有力武器[1]。俯冲段作为高超声速飞行器整个飞行阶段的最后一段，直接决定着整个作战任务的成败。战场环境下要求该飞行器具有良好的突防能力以应对地面防空系统的威胁，一方面提高飞行速度以实现快速突防[2]，另一方面要以特定方向攻击敌方防御薄弱的方向，以增强对目标的打击效果。

针对以上制导问题，文献[3]在建立相对运动方程的基础上，将机动弹头再入制导问题转化为最优控制问题，获得了最优制导律。文献[4]提供了一种满足指定方向攻击的三维自适应比例导引方法。文献[5]设计了一种具有末端落角和入射角约束的三维最优滑模制导律，但该方法在某些情况下会存在能量消耗过大的问题。文献[6-8]考虑不确定性因素的影响，将最优导引律与滑模变结构控制相结合，推导了满足终端落角约束的三维最优滑模制导律。文献[9-12]运用不同的方法实现了满足落角落速约束的俯冲制导律，但均未考虑终端方位角约束。全方位俯冲制导对于进攻敌方防守薄弱方向以及隐蔽在特殊地形的目标具有良好的杀伤效果。从目前俯冲制导方法的研究可见，对全方位俯冲制导方法的研究并不多见。

本文以大升阻比高超声速飞行器为研究对象，充分借鉴机动弹头制导律的研究方法及思路，结合此类飞行器的飞行特征研究其俯冲制导方法，考虑入射方位角约束，利用最优控制以能量损耗最小为性能指标推导全方位攻击导引方程。为避免该制导律在某些情况下存在的能量过度损耗，进一步利用对称原理获得全方位俯冲制导策略，最终对制导精度进行仿真分析。

1 全方位俯冲制导律

1.1 俯冲段相对运动方程

为了简化制导问题，将俯冲段运动分解到俯冲平面及转弯平面内，如图 1所示，定义俯冲平面为飞行器质心O1、目标Oo和地心OE所确定的平面，转弯平面定义为过目标Oo和飞行器质心O1而垂直于俯冲平面的平面[3]。

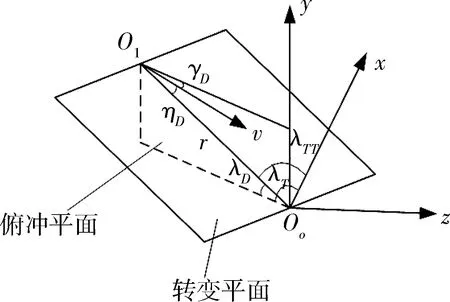
图1 俯冲平面与转弯平面示意图

图中，v为速度矢量；γD为速度倾角；λD为俯冲平面内的视线角；ηD为速度方向在俯冲平面的投影与视线间的夹角；γT为速度在转弯平面内的方向角，北向逆时针为正，顺时针为负；λTT为转弯平面内的视线角，ηT为速度矢量在转弯平面内的投影与俯冲平面的夹角，r为相对距离。相对运动方程为[3]：

(1)

1.2 全方位导引方程

在满足终端落点约束的同时，还要满足终端速度倾角和入射方位角约束才能实现三维全方位攻击。文献[3]提出了带有终端速度倾角约束的机动弹头的制导律，其导引方程如下：

(2)

式中，γDF为终端速度倾角，Tg为待飞时间。

对于高超声速飞行器全方位俯冲制导，上述俯冲平面导引同样适用。在转弯平面内，为实现全方位攻击，就要满足终端速度在转弯平面的方位角约束，因此取状态量

(3)

(4)

由于转弯必然造成能量的损耗，故选取能量最优性能指标为：

(5)

其中，tf为终端时刻，x(tf)Fx(tf)为补偿函数，F为半正定常值矩阵。根据极大值原理，线性系统二次型性能指标的最优控制律为：

(6)

在此，R=1，P可由Ricatti微分方程求解得出，最终可得转弯平面最优导引律

(7)

综合文献[3]中的俯冲平面导引律可得全方位攻击导引律

(8)

2 全方位俯冲制导策略

利用方程(8)导引飞行器进行全方位俯冲制导，如图 2所示，俯冲段开始飞行器在目标西南方向的点S处。实粗线、实细线、虚线和点划线分别为从目标点的西南、西北、东北和东南方向进行攻击的示意轨迹。

图2 改进前全方位攻击示意图

由图 2可知，当起始点在第3象限，入射方位角在第4象限(即图 2中点划线)时，飞行器需要顺时针绕很大角度才达到目标点，而没有逆时针转较小的角度,这必然会造成能量的过度损耗。

针对这一问题，首先分析其产生的原因。方程(8)的第2式中，右边第1项的作用是消除航向误差以精确命中目标，右边第2项的作用是使飞行器满足终端方位角约束。当起始点在第3象限，入射方位角在第4象限时，第2项将是一个较大的负值，该值绝对值较第1项大，从而将飞行器导引到使γT减小的方向，即顺时针方向。

要想将飞行器逆时针转到相应的角度上，可利用对称原理。如图 3所示，起点在第3象限，入射方位角在第4象限与入射方位角在第2象限的关于线段ST对称。因此，只需将方程(8)第2式相应的角度转变成入射方位角在第2象限的情况即可。

图3 利用对称原理改进全方位攻击示意图

(9)

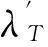
(10)

当飞行器位于第4象限时，

(11)

(12)

(13)

同时,为了实现全方位攻击，主导方位的比例系数2需要适当调整，其调整值可通过多次仿真确定，以同时满足方位和落点的精度要求。

对于起点和入射方位角在其他象限的情况，仍可运用方程(8)进行导引。以上便是全方位俯冲制导策略。

3 仿真分析

3.1 全方位俯冲制导律验证

运用文献[3]中的三自由度运动模型，采用CAV-H[13]总体及气动参数，取俯冲段起始经纬度λ0=φ0=0°，高度h0=40km，速度v0=2000m/s，速度倾角θ0=0°，航迹偏航角σ0=-45°；攻角α∈[0°,20°]，目标经纬度λf=φf=1°，落角约束λDF=-60°。设最大法向过载为20g。为了验证全方位俯冲制导律，选取终端速度方位角γTF分别为-45°和-135°。

图4和5分别给出了不同方位攻击的经纬高曲线和经纬度曲线；由图4和5可知，全方位俯冲制导律可以实现全方位攻击。γTF越大，需要转的角度也随之增大。

图6给出了不同方位攻击时攻角和倾侧角随时间变化曲线，开始攻角处于饱和状态以增大升力；弹体进行翻转时攻角随之迅速减小，以实现更加快速的翻转；为了实现转弯，攻角呈现出先增大后减小的变化规律。由于开始方位角与终端约束相差较大，倾侧角先达到-90°，以提供较大的侧向过载进行转弯，而纵向过载较小以使飞行器下压；随着方位角与终端约束之差变小，航向误差变大，倾侧角翻转以提供消除航向误差，并满足终端约束所需的侧向过载。图7给出了不同方位攻击时速度倾角随时间变化曲线，开始速度倾角减小相对平缓，倾侧翻转时有小幅度增大，之后减小速度加快，直到满足终端速度倾角约束。图8给出了不同方位攻击时总法向过载随时间变化曲线，在全方位攻击时，为了调整方向进行螺旋转弯，总法向过载在中间会出现一个极值，该值远小于最大过载约束，由此可见全方位攻击的可实现性。

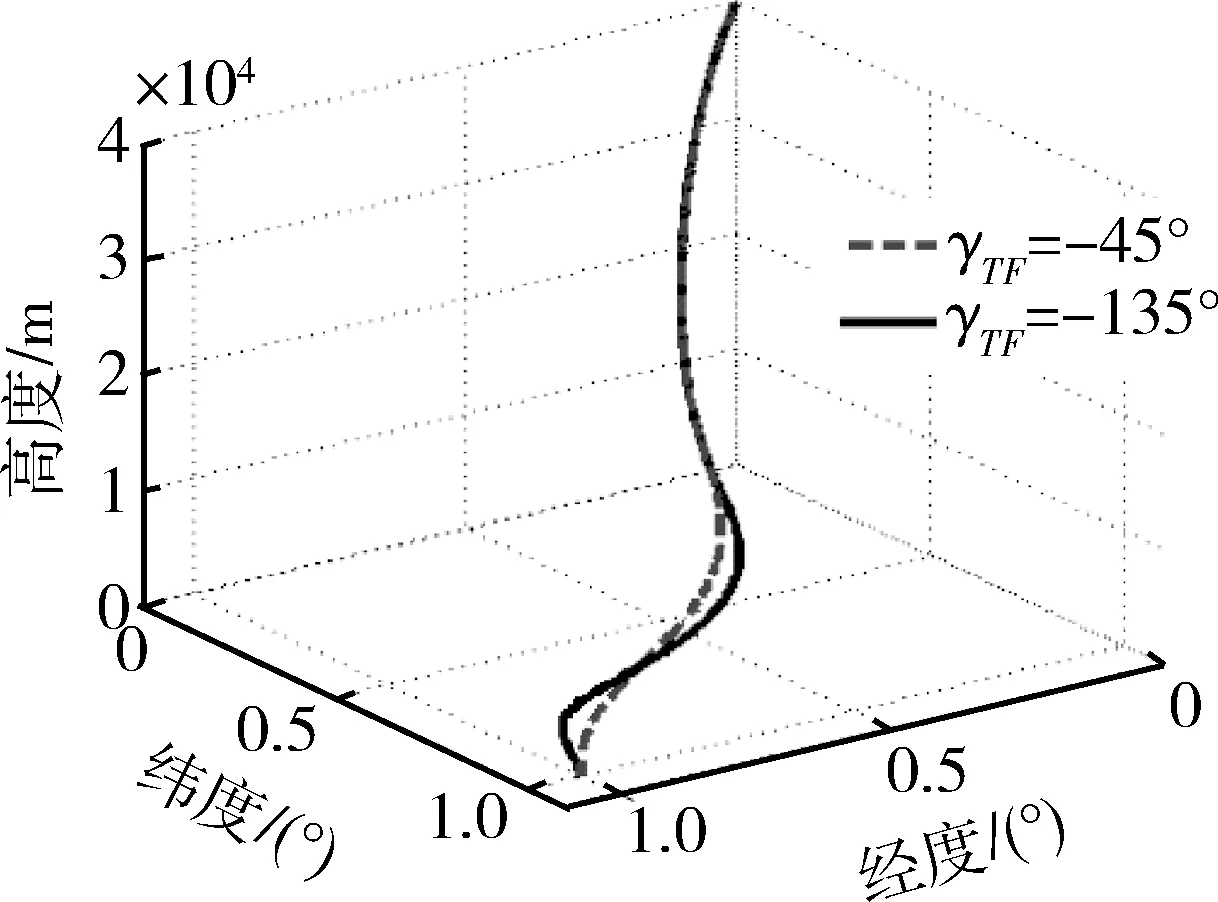
图4 不同方位攻击的经纬高

图5 不同方位攻击的经纬度

图6 不同方位攻击控制量随时间变化

图7 不同方位攻击速度倾角随时间变化

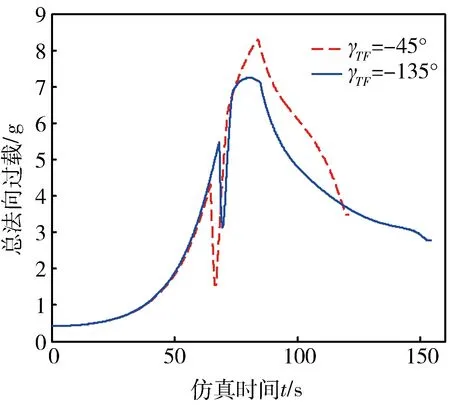
图8 不同方位攻击总法向过载随时间变化

运用全方位俯冲制导律获得不同入射方位角下的终端信息如表1所示。

表1 全方位俯冲制导律不同入射方位角的终端信息

从图5和表1可以看出，在γTF=-135°的情况下，正如上文所述，由于转动角度过大而导致过多的能量损耗，终端速度只有358.26m/s。由表1的数据可知，全方位俯冲制导律可实现对目标的全方位攻击并能满足终端约束。

3.2 全方位俯冲制导策略验证

为了验证全方位俯冲制导策略，进行如下仿真：俯冲段起始点经纬度分别取为(0°,0°)，(0°,2°)，(2°,0°)，(2°,2°)，高度h0=40km，速度v0=2000m/s，速度倾角θ0=0°，对应航迹偏航角σ0取为-45°，135°，45°，-135°。目标经纬度(1°,1°)，入射高低角约束λDF=-75°，入射方位角γTF分别为180°，135°，90°，45°，0°，-45°，-90°，-135°，-180°。其他约束条件与3.1节的仿真约束条件相同。在该组仿真条件下，飞行器从目标的4个不同方向，以9个不同的入射方位角对目标进行攻击，从而全面验证全方位俯冲制导策略。

图9 运用制导策略获得的攻击平面图

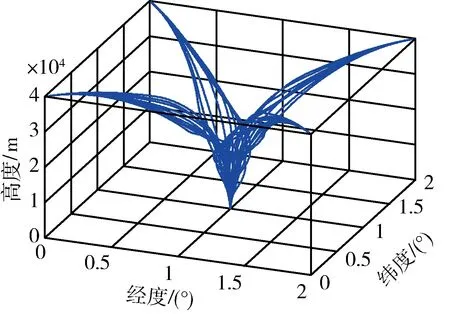
图10 运用制导策略获得的攻击三维图

图11 运用制导策略获得的总法向过载变化

图9和10分别给出的了运用全方位俯冲制导策略获得的平面图和三维图；从图中可以看出，运用该策略可以实现从目标不同方位发射，以不同入射方位角攻击目标。图11给出了运用全方位俯冲制导策略获得的总法向过载随时间的变化；每种情况的总法向过载均小于最大法向过载约束。表2给出了起点在第3象限，入射方位角在4个象限时的部分终端信息；对于入射方位角在第4象限的情况，终端速度明显提高，且终端约束均得到满足。综上可知，该制导策略以较小的能量损耗实现了全方位攻击，且能满足终端约束。

表2 全方位俯冲制导策略不同入射方位角的终端信息

4 结论

研究了高超声速飞行器全方位俯冲攻击问题。以能量损耗最小为性能指标推导出全方位攻击最优制导律；为了避免该制导律在某些情况下存在的能量过度损耗，进一步利用对称原理获得全方位俯冲制导策略。仿真结果表明该策略能够高精度地满足终端多种约束，并能以较少能量损耗实现全方位俯冲攻击。综上可知，该方法比传统俯冲制导方法更加灵活多变，可为高超声速飞行器俯冲段精确制导提供参考。

[1] George R. The Common Aero Vehicle: Space Delivery System of the Future [C] //Proc. of the AIAA Space Technology Conference & Exposition, 1999:1-11.

[2] 李响，柳长安.导弹俯冲段弹道分析与最优设计[J]. 北京理工大学学报, 2006, 26(9): 773-776. (Li Xiang, Liu Chang-an. Analysis and Optimum Design of the Dive Trajectory for a Cruise Missile [J]. Transactions of Beijing Institute of Technology, 2006, 26(9):773-776.)

[3] 赵汉元.飞行器再入动力学和制导[M].长沙: 国防科技大学出版社, 1997.

[4] Lu P, Doman D B, Schierman J D. Adaptive Terminal Guidance for Hypervelocity Impact in Specified Direction [J]. Journal of Guidance, Control, and Dynamics, 2006,29 (2):269-278.

[5] 张一，张合新，范金锁，黄金峰.带末端角约束的三维最优滑模制导律设计[J].科学技术与工程, 2010, 10(25): 6177-6180.(Zhang Yi, Zhang Hexin, Fan Jinsuo, Huang Jinfeng. Three-dimensional Optimal Sliding Mode Guidance Law Design with Terminal Angle Constraint[J].Science Technology and Engineering, 2010, 10(25): 6177-6180.)

[6] 胡正东，郭才发，蔡洪.带落角约束的再入机动弹头的复合导引律[J].国防科技大学学报, 2008, 30(3): 21-26. (Hu Zhengdong, Cuo Caifa, Cai Hong. Integrated Guidance Law of Reentry Maneuvering Warhead with Terminal Angular Constraint[J]. Journal of National University of Defense Technology, 2008, 30(3): 21-26.)

[7] 窦荣斌，张科.基于二阶滑模的再入飞行器末制导律研究[J].宇航学报, 2011, 32(10): 2109-2114. (Dou Rongbin, Zhang Ke. Research on Terminal Guidance for Re-Entry Vehicle Based on Second-Order Sliding Mode Control[J].Journal of Astronautics, 2011, 32(10): 2109-2114.)

[8] 范金锁，张合新，孟飞，吕永佳.飞行器最优末制导律的自适应PID滑模设计[J].宇航学报, 2012, 33(9): 1125-1232. (Fan Jinsuo, Zhang Hexin, Meng Fei, Lv Yongjia. Adaptive PID Sliding Mode Control Design for Vehicle Terminal Optimal Guidance Law[J]. Journal of Astronautics, 2012, 33(9): 1125-1232.)

[9] Zhu Jianwen, Liu Luhua, Tang Guojian, Bao Weimin. Optimal Guidance with Multi- targets for Hypersonic Vehicle in Dive Phase[C].6th RAST, Turkey, 2013: 341-346.

[10] 付主木，曹晶，张金鹏，董继鹏.带落角和落点约束的空地导弹最优制导律设计[J].航空兵器, 2014, (1): 3-6.(Fu Zhumu, Cao Jing, Zhang Jinpeng, Dong Jipeng. Design of Optimal Guidance Law with Impact Angle and Final Position Constraints for Air to Ground Missile[J]. Aero Weaponry, 2014, (1): 3-6.)

[11] 杨良，郑宗贵，徐衡，陈万春，周浩.多约束在线高斯伪谱末制导方法[J].弹道学报, 2014, 26(3): 98-103.(Yang Liang, Zheng Zonggui, Xu Heng, Chen Wanchun, Zhou Hao. Onboard Gauss Pseudospectral Terminal Guidance Law With Multiple Constraints[J]. Journal of Ballistics, 2014, 26(3): 98-103.)

[12] 刘开封，陈颖，梁立威，孟海东.滑翔弹头末段俯冲导引律设计与仿真[J].弹箭与制导学报, 2014, 34(3): 25-28.(Liu Kaifeng, Chen Ying, Liang Liwei, Meng Haidong. Design and Simulation of Diving Guidance Law for Terminal Phase Trajectory of Glide-warhead[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(3): 25-28.)

[13] Phillips T H. A Common Aero Vehicle (CAV) Model, Description, and Employment Guide[R]. Schafer Corporation for AFRL and AFSPC, 2003.

All-Directions Diving Guidance for Hypersonic Vehicles

Shen Lianjie, Liu Luhua, Tang Guojian, Zhu Jianwen

National University of Defense Technology, Changsha 410073, China

Anoveldivingguidancealgorithmwhichcanfulfilltheterminalimpactpointandangleconstraintsforhypersonicvehiclesisproposedinthispaper.All-directionsattackoptimalguidancelawsarederivedfromoptimalcontroltheorywithminimumenergyasperformanceindexestosatisfythedifferentterminalconstraintssynchronously.Furthermore,bytakingadvantageofsymmetryprinciple,theguidancestrategyisimprovedtoavoidwasteofenergyinsomecases.Finally,simulationexperimentswithCAV-Hareimplemented,theresultsshowthatthismethodcannotonlymeetavarietyofterminalconstraintsaccuratelyandbutalsoachieveall-directionsdivingattack.Theresultsshowthattheproposedstrategycanserveasareferenceforhypersonicvehiclesprecisionguidanceindivephase.

Hypersonicvehicles;Divingguidance;All-directions;Multipleconstraints

2015-05-19

申连杰(1990-)，男，陕西渭南人，硕士研究生，主要研究方向为飞行动力学、制导与控制；刘鲁华(1977-)，男，西安人，副教授，主要研究方向为飞行动力学、制导与控制；汤国建(1964-)，男，江苏金坛人，教授，博士生导师，主要研究方向为飞行动力学、制导与控制；朱建文(1987-)，男，甘肃定西人，博士研究生，主要研究方向为飞行动力学、制导与控制。

V448.235

A

1006-3242(2016)02-0054-06