高超声速再入飞行器抗饱和控制系统设计*
杜立夫 蔡高华 黄万伟 王丹晔
北京航天自动控制研究所,北京100854
高超声速再入飞行器抗饱和控制系统设计*
杜立夫 蔡高华 黄万伟 王丹晔
北京航天自动控制研究所,北京100854

针对高超声速再入飞行器纵向静不稳定模型,在考虑气动执行机构饱和非线性特性的情况下,研究了一种基于补偿方案的抗饱和控制系统设计方法。该方法把系统输入饱和特性视为不确定性,采用H∞回路成形技术设计了标称控制器;然后针对标称控制器与被控对象所组成的闭环系统进行补偿器设计;最后基于高超声速再入飞行器纵向静不稳定模型验证了该补偿方案的有效性。 关键词 高超声速;再入飞行器;输入饱和;扇形界;线性矩阵不等式;抗饱和补偿器
飞行器控制系统设计过程中,执行机构的饱和非线性特性可能是最需要关注和考虑的,执行机构的饱和特性会降低控制系统的性能,甚至使系统失稳。针对此类问题,设计抗饱和补偿器是一种较常见的方法。抗饱和补偿方法在忽略饱和非线性的情况下设计一个标称控制器,然后设计抗饱和补偿器来减小忽略饱和特性对闭环系统带来的负面影响。采用该方法可以在考虑控制输入饱和特性的情况下保证闭环系统的稳定性,达到期望的设计需求。
早期的抗饱和控制技术一般缺少严密的稳定性分析与清晰的系统性能分析,并且控制器求解过程比较繁琐[1-2]。文献[3]采用扩展的圆准则给出了一种基于线性矩阵不等式的静态补偿算法,但是该方法只是针对开环稳定系统提出的,限制了其工程适应性,但是对于系统静不稳定的情况,无法保证系统的全局稳定[4-5]。文献[6]针对稳定模型设计了基于LMI的动态补偿器,保证了系统稳定,并保证系统输出对外部干扰具有L2增益的鲁棒性。Hencey等[7-9]利用LMI区域法研究了抗饱和稳定问题。
本文针对高超声速再入飞行器引入了抗饱和补偿控制系统的设计方法。首先,给出高超声速再入飞行器的纵向通道模型,其次,采用扇形界约束条件描述了控制输入的饱和特性,并进行了考虑执行机构饱和特性情况下的系统鲁棒稳定性与性能分析,给出了补偿控制器的存在条件与构造方法,最后,采用高超声速再入飞行器纵向通道动力学模型对该方法的合理性与有效性进行了仿真验证。
1 高超声速飞行器纵向运动模型与气动特性分析
考虑地球曲率半径与地球自转,高超声速再入飞行器纵向通道非线性动力学模型如式(1)所示[10-11]:
(1)

针对高超声速再入飞行器纵向通道非线性动力学模型,进行小扰动线性化,得到系统纵向通道线性动力学方程为:
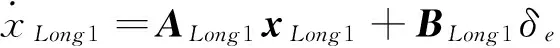
(2)
其中,模型系统矩阵与控制矩阵中各项系数表达式如下所示:
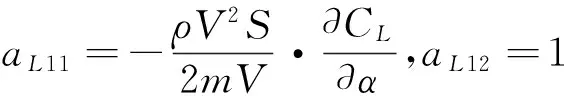


(3)

可见,对于高超声速再入飞行器俯仰动力学模型而言,系统静不稳定。下面将在考虑气动执行机构饱和特性的情况下,给出补偿控制器的设计过程。
2 考虑执行机构饱和特性情况下的系统鲁棒性能分析
定义u为控制系统的连续输入量,umax为执行机构饱和值,饱和函数sat(·)定义为:
(4)
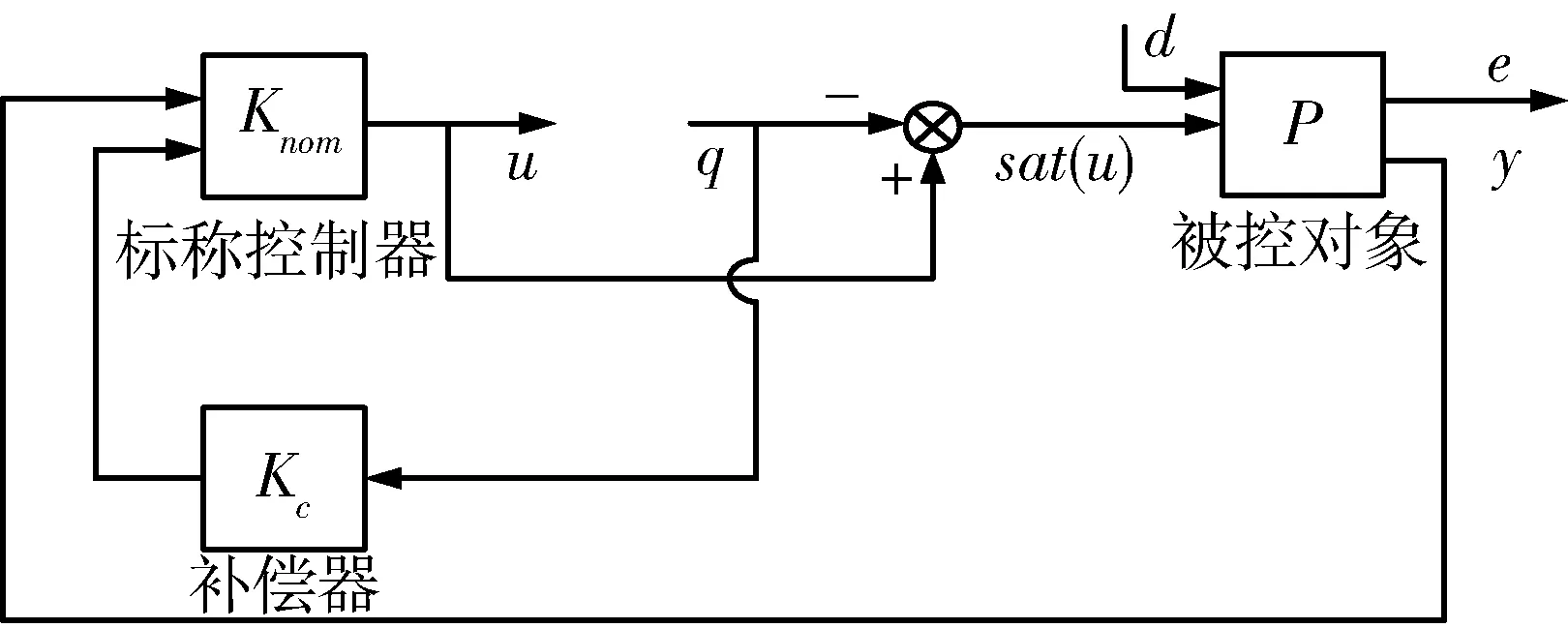
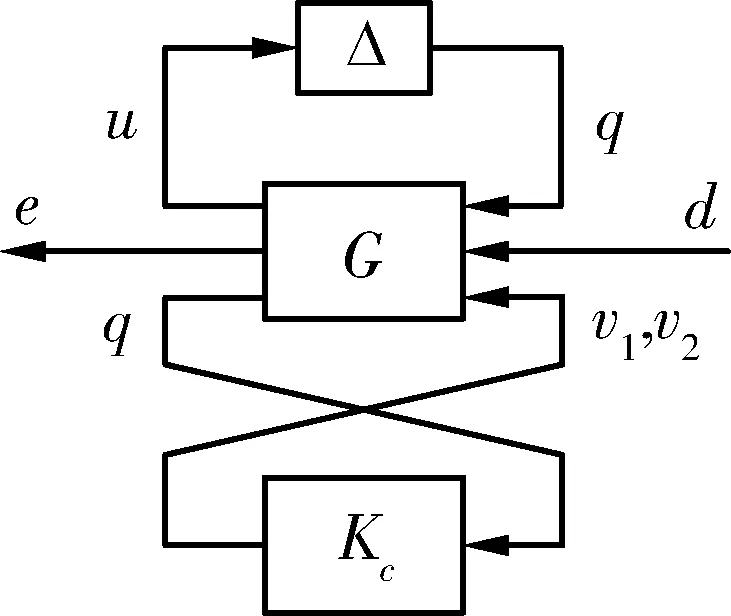
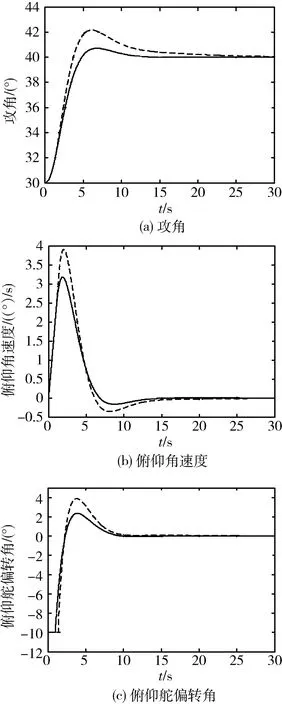
定义σ(u)=sat(u)为具有饱和特性的系统输入;q=u-sat(u)为系统饱和输入引起的误差,q满足q=ψ(u),其中ψ为扇形界不确定性算子,ψ∈sect [0K],K=diag{k1,k2,...,knu},0 qTT(u-q)≥0 (5) 考虑如下所示具有扇形不确定性的线性时不变系统: (6) 其中,x∈Rn是系统状态,d∈Rnd是外界扰动输入,e∈Rne是控制输出。 对于线性不确定系统式(5)和(6),下面的定理[5]可决定其鲁棒稳定性与鲁棒性能,该定理可由Lyapunov稳定性理论与Schur补引理得到。 <0 (7) 考虑如下所示的线性时不变被控对象P: (8) 其中,xp∈Rnp是被控对象状态,y∈Rny是量测输出,σ(u)∈Rnu是考虑饱和特性的系统输入,e∈Rne是外界输出,d∈Rnd是外界输入。在这里,假设系统满足如下3个条件: 1) (Ap,Bp2,Cp2)可镇定可观测; 3)Dp22=0。 图1 控制结构框图 图2 控制结构框图 图3 控制结构一般框图 本文的控制结构框图如图1所示,对图1进行等效转换,得到控制结构等效框图如图2所示。在忽略饱和非线性的情况下,首先设计标称控制器Knom,该标称控制器设计可以采用一般的线性控制系统设计方法,所设计的标称控制器Knom在忽略输入饱和特性的情况能稳定开环系统P,且决定着系统的性能指标。假设该标称控制器存在且具有如下形式: (9) 其中,xk∈Rnk是标称控制器状态,v1,v2是由补偿器Kc提供的辅助输入。 设计补偿器Kc的目的是在一定的性能指标下,减小输入饱和非线性对标称控制器的不利影响。假设所设计的补偿器具有如下形式: (10) 其中,xc∈Rnc是补偿器状态。 将执行机构连续输入量u与q之间的关系用非线性关系式Δ=(1-σ(u))/u来表示,即q=Δ·u,则图2所示的控制结构框图可以转化为图3所示的控制结构一般框图。其中G为不含补偿器Kc情况下由开环系统P与标称控制器Knom所组成的闭环系统,G的状态空间方程如下所示: (11) 其中,x∈Rn,n=np+nk,且: (12) 式(12)中的状态空间矩阵可表示为如下形式: (13) 由式(13)可以看出,闭环状态空间矩阵与补偿器的状态空间矩阵之间存在仿射关系,针对系统式(12)利用定理1给出的系统稳定条件,下面的定理[5]给出了补偿器的存在条件。 (14) (15) (16) 由定理2得到R11,S与γ之后,定理3给出了 补偿器状态空间矩阵的构造方法[5]。 定理3 对于给定的R11,S,γ与V=T-1,令MNT=In-RS,其中:M,N∈Sn×np,HT=[Inp0],那么np阶补偿器可通过下面3个步骤构造得到: (17) (18) (19) (20) 3)最后计算得到补偿器状态空间矩阵为: (21) 高超声速再入飞行器纵向通道系统模型标称控制器与补偿器设计框图如图4所示,其中:wc是控制加权,wn是噪声加权,wp是性能加权,xtc是跟踪指令,noise是外部噪声。 图4 标称控制器与补偿器设计框图 对于飞行器纵向通道系统模型,xtc为攻角跟踪指令αc,首先设计标称控制器,采用式(3)中给出的Ma=15处的纵向通道系统线性模型,各加权函数选择如下: wp=0.2(s+10)/(s+0.01),wc=1/10,wn=0.001。 忽略执行机构的饱和非线性特性,采用鲁棒控制中的H∞回路成形(Loop Shaping)技术设计标称控制器,得到纵向标称控制器为: KL.nom=-3.0742(s+0.3735)/(s+1.567) (22) 选取K=0.994,采用定理3给出的补偿器设计方案步骤,得到纵向系统补偿器系统矩阵为: 高超声速再入飞行器纵向通道模型为静不稳定,且飞行器进行大攻角再入飞行,纵向通道的控制目标是在执行机构存在饱和的情况下完成攻角指令跟踪,并且保持高性能的稳定飞行。由仿真图可以看出,通过对标称控制器加抗饱和补偿器与未加补偿器的纵向控制系统进行比较,所设计的抗饱和补偿器实现了纵向通道的稳定飞行,飞行性能得到了提高,攻角的超调量与调节时间都有所减小,并且俯仰角速度变化反应的动态过程得以改善,舵偏角进入饱和时间减小,所设计的纵向控制系统实现了较好的控制效果。 图5 纵向通道控制系统仿真图 针对高超声速再入飞行器纵向静不稳定模型,在考虑气动执行机构饱和非线性特性的情况下,研究了一种基于补偿方案的控制系统设计方法。采用扇形界约束条件描述了控制输入的饱和特性,采用H∞回路成形技术设计了标称控制器,然后针对标称控制器与被控对象所组成的闭环系统进行了补偿器设计,给出了补偿控制器的存在条件与构造方法,并采用高超声速再入飞行器纵向通道动力学模型对该方法的合理性与有效性进行了仿真验证。仿真结果表明,所设计的控制系统在控制输入饱和的情况下对静不稳定系统具有较好的控制性能,有效地提高了系统的动态响应特性。 [1] Teel A R, Kapoor N. The L2 anti-windup problem: its definition and solution[C]//European Control Conference, 1997. [2] Tyan F, Bernstein D S. Anti-windup compensator synthesis for systems with saturation actuators[J]. International Journal of Robust Nonlinear Control, 1995, 5: 521-537. [3] Mulder E F, Kothare M V, Morari M. Multivariable anti-windup controller synthesisusing linear matrix inequalities[J]. Automatica, 2001, 37: 1407-1416. [4] Teel A R. Anti-windup for exponentially unstable linear systems[J]. International Journal of Robust Nonlinear Control, 1999,9: 701-716. [5] Wu F, Bei L. Anti-windup control design for exponentially unstable LTI systems with actuator saturation[J]. Systems & Control Letters, 2004, 52: 305-322. [6] Grimm G, Hatfield J, Postlethwaite I.Anti-windup for stable linear systems with input saturation: an LMI-based synthesis[J]. IEEE Transactions on Automatic Control,2003,48 (9):1509-1525. [7] Hencey B, Alleyne A G. A KYP lemma for LMI regions[J].IEEE Transactions on Automatic Control, 2007, 52(10): 1926-1930. [8] Hencey B, Alleyne A.An anti-windup technique for LMI regions[J].Automatica, 2009, 45(10): 2344- 2349. [9] Da Silva, Tarbouriech S. Anti-windup design with guaranteed regions of stability: an LMI-based approach[J]. IEEE Transactions on Automatic Control, 2005, 50(1):106-111. [10] Space Division Rockwell International. Aerodynamic design data book, Orbital Vehicle STS-1, Revision M, SD72-SH-0060[R]. November, 1980. [11] Cooke D R. Space Shuttle Stability and Control Test Plan[C]// Proc. of AIAA the 9th Atmospheric Flight Mechanics Conference, 1982. [12] 方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京: 北京航空航天大学出版社, 2005.(Fang Z P, Chen W C, Zhang S G. The Flight Dynamics of Aerodynamic Aircraft [M]. Beijing: Beihang University Press, 2005.) [13] 韩崇昭,张爱民,刘晓风.多变量反馈控制分析与设计[M].西安:西安交通大学出版社,2011: 316-330. (Han C Z, Zhang A M, Liu X F.Multivariable Feedback Control: Analysis and Design[M]. Xi’an: Xi’an Jiao Tong University Press,2011:316-330.) Anti-Windup Compensation Control System Design for Hypersonic Reentry Vehicle Du Lifu, Cai Gaohua, Huang Wanwei, Wang Danye Beijing Aerospace Automatic Control Institute, Beijing 100854, China Ageneralizedsaturationcontroltechnologyintheframeworkofanti-windupcompensationisintroducedforthelongitudinalstatic-unstablemodelofhypersonicreentryvehiclecontrollerdesignsubjecttoinputsaturationnonlinearity.Firstly,thelongitudinalofhypersonicreentryvehicleisdescribedandsystemcharacteristicsanalysisarealsoimplemented.Then,robuststabilityandperformanceanalysisofclosed-loopsystemwithsector-boundednonlinearityareprovided,atwo-stepdesignprocedureforanti-windupcompensatorisgiven.Finally,closed-loopcontrolsystemsimulationsbyusingthelongitudinalstatic-unstablemodelofhypersonicreentryvehiclearemadetodemonstratetherationalityandeffectivenessofthegeneralizedanti-windupcontroltechnology. Hypersonic;Reentryvehicle;Inputsaturation;Sector-bounded;Linearmatrixinequality;Anti-windupcompensator *国家自然科学基金(6140355) 2015-06-10 杜立夫(1985-),男,辽宁人,博士研究生,主要研究方向为飞行器控制技术;蔡高华(1987-),男,河南人,博士,工程师,主要研究方向为制导控制系统设计;黄万伟(1970-),男,湖南人,博士,研究员,主要研究方向为先进控制理论与应用、导航与制导技术等;王丹晔(1984-),女,山西人,硕士,工程师,主要研究方向为制导控制系统设计。 TP273 A 1006-3242(2016)02-0009-06
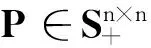

3 补偿器设计

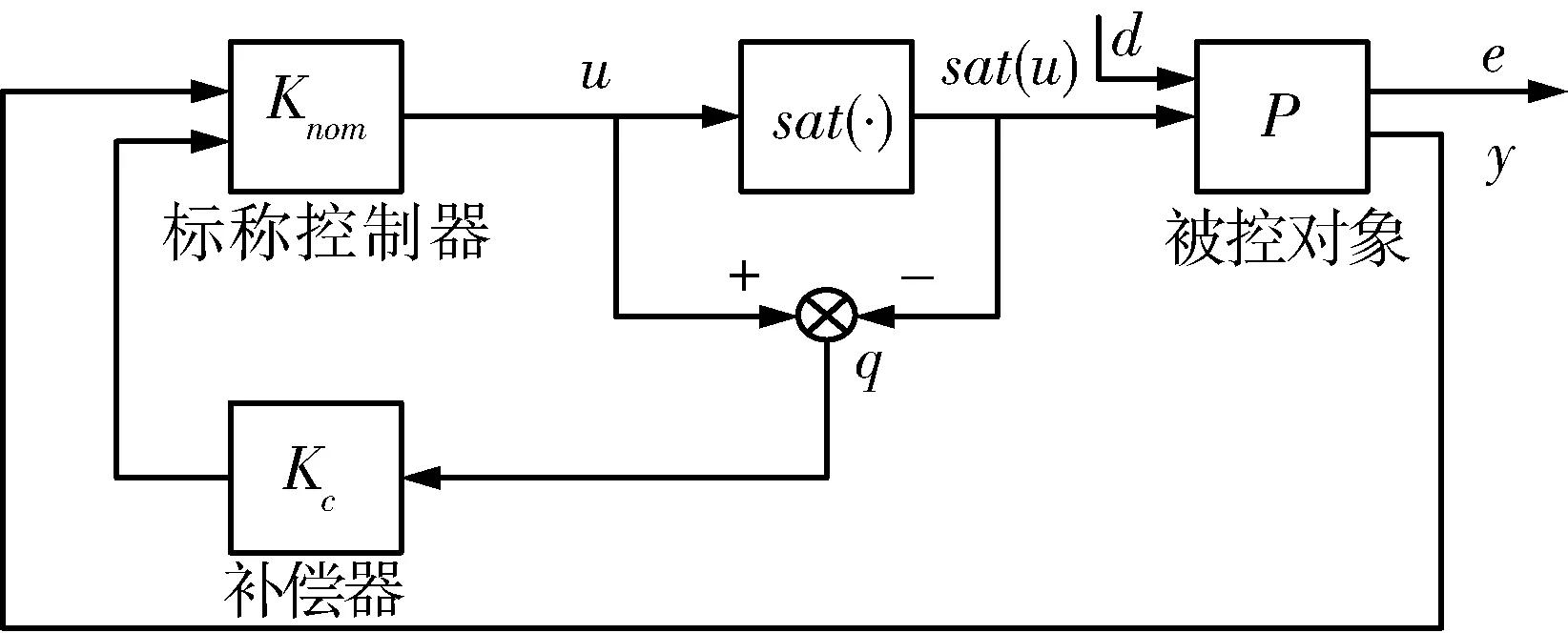
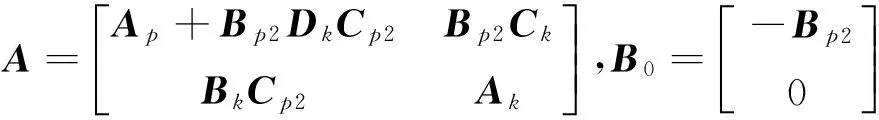




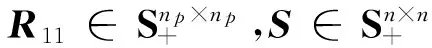
4 高超声速再入飞行器控制系统设计与仿真验证


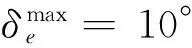
5 结论

