近地零动量卫星干扰力矩飞轮补偿控制

王献忠 张 肖 张丽敏

1.上海航天控制技术研究所，上海200233 2.空间智能控制技术重点实验室，上海200233



近地零动量卫星干扰力矩飞轮补偿控制

王献忠 张 肖 张丽敏

1.上海航天控制技术研究所，上海200233 2.空间智能控制技术重点实验室，上海200233

对于配置单翼太阳帆板的近地卫星，气动干扰力矩严重影响近地卫星姿态控制。首先进行对日定向时气动干扰力矩分析；接着针对气动干扰力矩设计飞轮补偿控制算法，并采取弱偏置措施防止飞轮过零干扰；最后通过仿真验证了干扰力矩补偿控制算法的有效性，并可大幅减小磁力矩器磁矩。 关键词 卫星；姿态控制；零动量控制；飞轮；磁力矩器

近地空间稀薄大气不仅会影响卫星轨道，还会对卫星姿态控制产生较大的气动干扰力矩，特别是安装单翼太阳帆板进行二维对日定向控制的近地卫星，如轨道高度200～300km的卫星，气动干扰力矩幅值可达100g·cm。

磁力矩器只能进行二轴姿态控制，全磁控制一般用于星体角速率阻尼[1]，卫星稳态运行时一般采用飞轮加磁控制[2]。不需要快速姿态机动的卫星一般采用偏置动量控制，偏置动量卫星磁力矩器用于动量轮卸载和章进动控制[3-5]；目前较多卫星采用零动量控制，零动量卫星磁力矩器一般用于对飞轮角动量卸载[2，6]，国内外学者也对磁和飞轮联合控制进行了研究[7-10]，磁和飞轮联合控制时磁力矩器除了对飞轮卸载，还直接用于星体姿态控制。

气动力与卫星相对大气的飞行速度方向相反，产生的气动干扰力矩与卫星的飞行速度方向正交，一般作用在卫星的Z轴。考虑到太阳矢量基本在卫星赤道面附近，近地卫星对日定向时气动干扰力矩峰值一般出现在高纬度区，此区域Z轴磁场强度最强，X和Y轴磁场强度较弱，根据磁矩的叉乘特性Tm=M×B，Z轴姿态处于磁不可控区，气动干扰力矩主要由飞轮转速控制。

近地卫星气动干扰力矩严重，直接基于零动量加磁卸载控制，要求配置较大磁矩输出的磁力矩器，导致磁力矩器的重量大幅增加。本文首先分析近地卫星对日定向时的气动干扰力矩；接着针对气动干扰力矩研究了飞轮补偿控制算法和防止飞轮过零干扰；最后仿真验证了干扰力矩补偿控制算法的有效性。

1 动力学方程及磁卸载

1.1 刚体动力学方程

卫星刚体动力学模型[11-12]如下：

(1)

其中，I是卫星本体的转动惯量，ω为卫星本体坐标系相对惯性空间的角速率，H为飞轮角动量，Tc为姿控力矩，Td为干扰力矩。

1.2 飞轮磁卸载

飞轮角动量磁卸载如下：

Mc=-k·(Bb×Δh)

(2)

其中：Δh为需要卸载的飞轮角动量，k为磁卸载系数，Bb为卫星本体下三轴磁场强度，Bb=[BxByBz]T，Bx，By，Bz为磁场强度三轴分量。

2 对日定向时气动干扰力矩分析

2.1 太阳矢量计算

太阳在惯性系和轨道系下指向如图1所示。

太阳矢量在惯性系下坐标：

(3)

其中：αs为太阳赤经，βs为太阳赤纬。

将rsi转换至轨道坐标系下：

(4)

图1 太阳在惯性系和轨道系下指向

其中：Aoi为惯性系至轨道系的转换矩阵，i，u，Ω分别为卫星的轨道倾角、纬度辐角和升交点赤经。

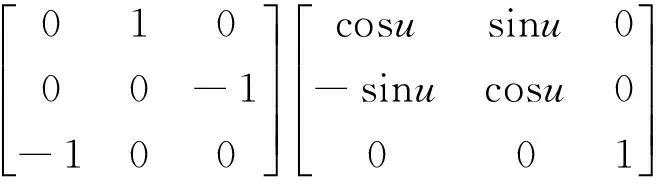
2.2 二维对日定向时帆板法线方向

帆板在星体上安装方式及零位位置如图2所示，帆板可以绕偏置轴最大正负70°偏置，可以绕旋转轴正负360°旋转。

图2 帆板在星体上安装方式及零位位置

二维对日定向时帆板先绕Yb轴旋转，使太阳矢量位于OsYsZs平面内，再绕偏置轴偏置一定的角度，使帆板法线指向太阳。

不考虑卫星对地定向时星体姿态偏差(下同)，卫星在轨时相对惯性空间按一定的轨道角速率绕轨道面法向(负Yo轴)旋转，太阳相对惯性空间静止，帆板需要绕轨道面负法向(Yo轴)旋转才能保持帆板对日定向。

升交点处帆板二维对日定向先绕Yb轴旋转角度u0，再绕Xb轴偏置角度β实现对日定向；卫星按轨道角速率ω0旋转，飞行到纬度幅角u处，帆板绕Yb轴旋转角度为u0+u，再绕Xb轴偏置角度β实现对日定向，帆板法线在轨道坐标系下坐标：

(5)

其中：

Ano为轨道系至帆板系的转换矩阵，rn0为帆板零位状态下帆板法线指向。

对日定向状态下帆板法线指向太阳，得：

rno=rso

(6)

由式(6)可得：

(7)

(8)

对于倾角为42°的近地轨道，考虑太阳南北回归23.5°影响，帆板最大偏置角度约为65.5°，一般要求帆板具备70°的偏置能力。

2.3 气动干扰力矩分析

气动干扰力和气动干扰力矩如下：

(9)

Tda=La×Fp

(10)

其中：cd为气动阻力系数 ，取值在2.2～2.4之间，ρ为卫星所在高度的大气密度，v为飞行器相对大气的速度，A为帆板受气动影响的等效面积，La为迎风面压力中心相对飞行器质心的距离。

气动干扰力矩作用在星体的Z轴，设帆板面积为s，帆板二维对日定向时等效气动面积如下：

(11)

由式(11)得Z轴气动干扰力矩如下：

(12)

其中：Tdaz0为气动干扰力矩幅值，单翼安装在相对飞行方向的左侧Tdaz0<0，反之右侧Tdaz0>0。

近地卫星单翼帆板气动干扰力矩较严重，采用双翼对称安装帆板，气动干扰力矩可以相互抵消。

3 干扰力矩控制

3.1 飞轮补偿控制

由式(12)可知，气动干扰力矩具有正弦绝对值波形，波动周期为轨道周期。当u+u0=90°，或u+u0=270°时气动干扰力矩最大。

考虑到太阳矢量基本在卫星赤道面附近，近地卫星对日定向时气动干扰力矩峰值一般出现在高纬度区，此区域Z轴磁场强度最强，X轴和Y轴磁场强度较弱，根据磁矩的叉乘特性Tm=M×B，Z轴姿态处于磁不可控区，气动干扰力矩主要由飞轮转速控制。

u0=0气动干扰力矩如图3所示，气动干扰力矩最大时磁控最弱，以下气动干扰力矩控制考虑u0=0的情况。

图3 气动干扰力矩曲线

近地卫星气动干扰力矩严重，直接基于零动量加磁卸载控制要求配置较大磁矩输出的磁力矩器，导致磁力矩器的重量大幅增加。

基于X轴飞轮偏置角动量与轨道角速率叉乘产生的陀螺力矩控制气动干扰，飞轮补偿控制力矩如下：

Tzb=-Hx·ω0

(13)

补偿角动量与根据滚动姿态角计算的飞轮控制量合成后控制X轴飞轮，磁力矩器不对X轴飞轮补偿角动量卸载。

X轴飞轮偏置角动量用于磁不可控区干扰力矩补偿，为避免X轴飞角动量变化对X轴干扰，磁可控区X轴飞轮角动量保持不变，针对气动干扰力矩设计飞轮补偿角动量如图4所示。

图4 补偿气动干扰力矩X轴飞轮角动量偏置曲线

由式(12)和(13)可得X轴飞轮角动量补偿最大值如下：

(14)

其中：Tdaz0为气动干扰力矩最大值。

Z轴干扰力矩磁不可控区出现在南北极附近的较小区域内，磁可控区X轴飞轮角动量保持值产生的补偿力矩幅值大于气动干扰力矩平均值。由式(12)得到气动干扰力矩均值如下：

(15)

由式(15)得X轴飞轮角动量保持值要求如下：

(16)

针对气动干扰力矩的飞轮角动量补偿策略也可以应用于受地球阴影遮挡的太阳光压干扰力矩补偿，受地球阴影遮挡的太阳光压干扰力矩如图5所示，相应X轴飞轮角动量偏置曲线如图6所示，X轴飞轮角动量保持值可以适当减小。

图5 太阳光压干扰力矩曲线

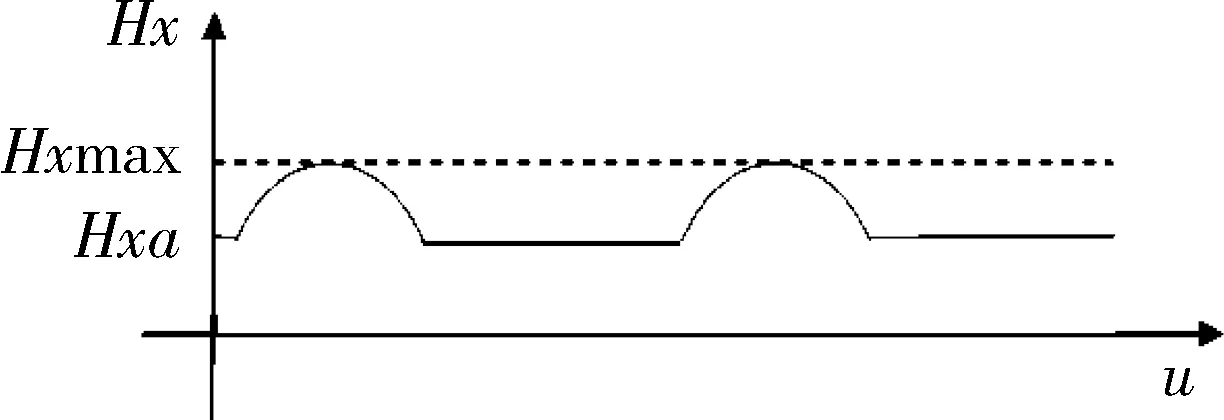
图6 补偿光压干扰力矩X轴飞轮角动量偏置曲线

3.2 飞轮过零抑制

飞轮转速过零时，动摩擦转变为静摩擦，再由静摩擦转变为动摩擦，且正反转摩擦力矩极性相反，飞轮转速过零会对星体姿态控制产生干扰，影响星体的稳定度，特别是当飞轮在零转速附近频繁控制时，飞轮转速频繁过零还会影响飞轮寿命。

为了避免飞轮转速过零，可以采用整星零动量方式，但整星零动量控制需要4台飞轮同时工作，采用3台飞轮避免转速过零安装方式如图7所示。

图7 避免飞轮转速过零安装方式

类似双自由度偏置动量控制，可以对俯仰轴角动量进行适当偏置Hb，根据斜装飞轮安装角得3台飞轮工作时中心角动量如下：

Hs=Hb/sinβ

(17)

Hx=-cosα·cosβ·Hs

(18)

Hy=-sinα·cosβ·Hs

(19)

斜装飞轮工作在弱偏置状态，可以避免转速过零，其对X和Z轴的角动量分量可以避免X和Z轴飞轮转速过零。

不考虑X轴飞轮对气动干扰力矩补偿，斜装飞轮弱偏置极性使俯仰轴角动量Hb为负；X轴飞轮对气动干扰力矩补偿角动量较大时，要使斜装飞轮在X轴的角动量与气动干扰力矩补偿角动量极性一致，降低X轴飞轮转速；反之要极性相反，避免X轴飞轮过零。

4 仿真验证

卫星偏航轴加幅值为-100g·cm的正弦绝对值气动干扰力矩，结合近地轨道角速率，理论计算X轴补偿角动量约为-5.5N·m·s，反作用飞轮角动量为15N·m·s。

不考虑飞轮补偿气动干扰力矩磁力矩器输出如图8所示，稳定时最大输出磁矩约300A·m2。

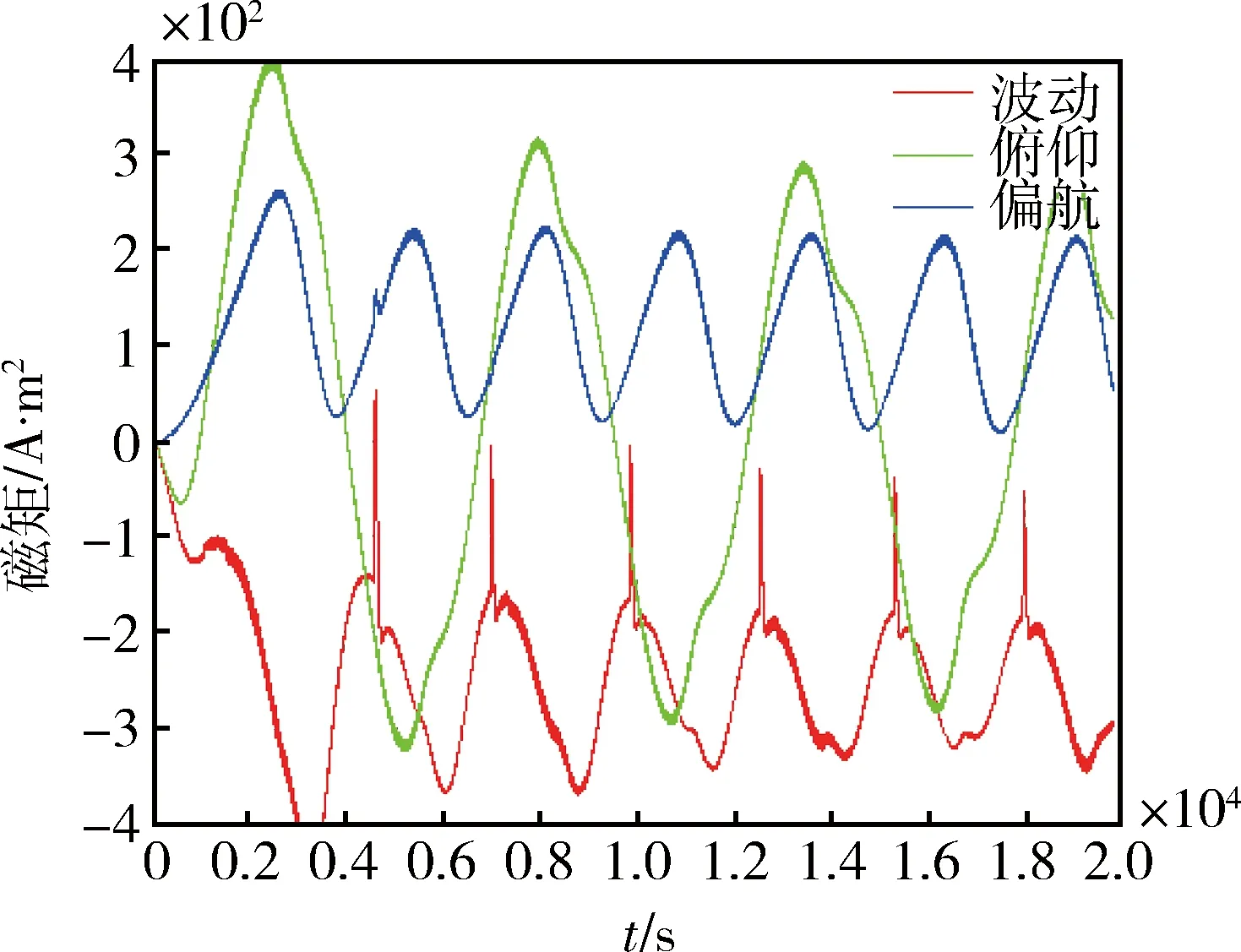
图8 不考虑飞轮补偿磁力矩器磁矩输出曲线

采用飞轮补偿气动干扰力矩磁力矩器磁矩输出如图9所示，稳定时最大输出磁矩约50A·m2，且稳态姿态控制精度也得到了提高。飞轮角动量输出曲线如图10所示，稳定时Y和Z轴飞轮转速会过零，可以通过Y轴弱偏置避免飞轮过零。

图9 考虑飞轮补偿磁力矩器磁矩输出曲线

图10 考虑飞轮补偿飞轮角动量输出曲线

5 结论

首先分析了近地卫星对日定向时气动干扰力矩；接着针对气动干扰力矩设计飞轮补偿控制算法，并采取弱偏置措施防止飞轮过零干扰；最后通过仿真验证了干扰力矩补偿控制算法的有效性，并可大幅减小磁力矩器磁矩，减轻卫星重量。

[1] 陈宏宇.无陀螺磁控小卫星的大角度姿态捕获研究[J].航天控制，2006，24(3)：43-47,53.(Chen Hongyu. Active Magnetic Attitude Control of Microsatellite Without Gyroscope[J].Aerospace Control, 2006，24(3)：43-47,53.)

[2] 田春华,马广富,李传江，等.三轴稳定卫星姿控系统的一般性问题[J].自动化技术与应用，2001，20(1)：9-12.(Tian Chunhua, Ma Guangfu, Li Chuanjiang, et al. General Problem of Three Axis Stabilized Satellite Attitude Control System[J]. Techniques of Automation and Applications, 2001，20(1)：9-12.)

[3] 柯旗,王勇,魏春岭.一种在轨改善偏置动量卫星控制精度的方法[J].空间控制技术与应用，2011，37(4)：41-44.(Ke Qi, Wang Yong, Wei Chunling. A Way to Improve Attitude Control Accuracy for Momentum Biased Satellite[J].Aerospace Control and Application, 2011，37(4)：41-44.)

[4] 黄卫东,张育林. 重力梯度稳定小卫星的最优主动磁控和动量轮控制[J].航天控制，2005，23(4)：27-31.(Huang Weidong, Zhang Yulin. An Optimal Control Algorithm of a Gravity Gradient Stabilized Small Satellite with Momentum Wheel and Magnetic Torque[J]. Aerospace Control, 2005，23(4)：27-31.)

[5] 李传江,马广富,宋斌.基于滚动信息反馈的偏置动量卫星滚动/偏航回路姿态控制器设计[J]. 航天控制，2006，24(3)：29-34.(Li Chuanjiang, Ma Guangfu, Song Bin. Roll/Yaw Attitude Controller Design of Biased Momentum Satellite Based on Roll Information Feedback[J].Aerospace Control, 2006，24(3)：29-34.)

[6] 李鹏奎,钱山,郭才发，等.零动量轮卫星姿态控制系统研究[J].中国空间科学技术，2009，29(2)：25-32.(Li Pengkui, Qian Shan, Guo Caifa ，et al. Research on Satellite Attitude Control Problems of Zero-momentum Reaction Wheel System[J]. Chinese Space Science and Technology, 2009，29(2)：25-32.)

[7] 贾飞蕾,徐伟,李恒年，等.基于联合飞轮和磁力矩器的航天器姿态控制算法研究[J].航天控制，2010，28(3)：16-19.(Jia Feilei, Xu Wei, Li Hengnian， et al. The Study of Control Algorithm for Spacecraft Attitude Control Based on the Combination of Reaction Wheels and Magnetorque[J].Aerospace Control, 2010，28(3)：16-19.)

[8] 陈闽,张世杰,张迎春.基于反作用飞轮和磁力矩器的小卫星姿态联合控制算法[J].吉林大学学报(工学版)，2010，40(4)：1155-1160.(Chen Min, Zhang Shijie, Zhang Yingchun. Combined Attitude Control Method of Small Satellite Using Reaction Wheels and Magnetorquers[J].Journal of Jilin University(Engineering and Technology Edition), 2010，40(4)：1155-1160.)

[9] 段晨阳,汤国建,张世杰.单轴飞轮故障时的小卫星姿态控制方法研究[J].航天控制，2007，25(3)：48-52.(Duan Chenyang, Tang Guojian, Zhang Shijie. Attitude Control Method of Small Satellite in the Case of Single Reaction Wheel Failure[J]. Aerospace Control, 2007，25(3)：48-52.)

[10] 陈闽,张世杰,邢艳军，等.飞轮故障时的小卫星轮控与磁控联合控制方法[J].哈尔滨工业大学学报，2007，39(5)：811～816.(Chen Min, Zhang Shijie, Xing Yanjun，et al. Combined Attitude Control Method of Small Satellite in the Case of Reaction Wheel Failed[J]. Journal of Harbin Institute of Technology, 2007，39(5)：811-816.)

[11] 章仁为.卫星轨道姿态动力学与控制[M].北京：北京航空航天大学出版社，2006.(Zhang Renwei. Attitude and Orbit Dynamics and Control of Satellite [M]. Bei Jing: Beihang University press, 2006.)

[12] 屠善澄.卫星姿态动力学与控制[M].北京：宇航出版社，2002.(Tu Shancheng. Attitude Dynamics and Control of Satellite [M]. BeiJing: Space press, 2002.)

Disturbance Moment Control Based on Wheel for Zero-Momentum Near Earth Satellites

Wang Xianzhong, Zhang Xiao, Zhang Limin

1.Shanghai Aerospace Control Technology Institute, Shanghai 200233,China 2.Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 200233,China

Theattitudecontrolofnearearthsatelliteswithsinglesolarcellarrayisbadlydisturbedbytheatmospheredisturbancemonment.Firstly,theatmospheredisturbancemomentofnearearthsatellitesisanalyzedwhilethenormaldirectionofthesolarcellarraypointstosun.Then,thecontrolarithmeticisdesignedforcompensatingthedisturbancemomentofatmospherebasedonwheelandpreventingfromtherotatespeedcrossing-zerodisturbanceofthewheelwithlowbiasedmomentum.Finally,thesimulationresultvalidatesthearithmeticofthedisturbancemomentcontrolandshowsthatthemagneticmomentofthemagnetorquercanbelargelydecreased.

Satellite;Attitudecontrol;Zero-momentumcontrol;Wheel;Magnetorquer

2015-06-30

王献忠(1971-)，男，江苏太仓人，博士，研究员，主要研究方向为航天器导航、制导与控制技术；张 肖(1981-)，女，浙江舟山人，硕士，高级工程师，主要研究方向为航天器控制技术；张丽敏(1981-)，女，河南新乡人，硕士，工程师，主要研究方向为航天器导航与控制技术。

V448.2

A

1006-3242(2016)02-0060-06