并行协作骨干粒子群优化算法
申元霞,曾传华,王喜凤,汪小燕
(1.安徽工业大学计算机科学与技术学院,安徽马鞍山 243032;2.安徽工业大学数理科学与工程学院,安徽马鞍山 243032)
并行协作骨干粒子群优化算法
申元霞1,曾传华2,王喜凤1,汪小燕1
(1.安徽工业大学计算机科学与技术学院,安徽马鞍山 243032;2.安徽工业大学数理科学与工程学院,安徽马鞍山 243032)
为解决骨干粒子群优化(Bare-Bone Particle Swarm Optimization,BBPSO)的早期收敛问题,本文通过粒子的运动行为分析了导致BBPSO早期收敛的因素,并提出并行协作BBPSO,该算法采用并行的主群和从群之间的协作学习来平衡勘探和开采能力.为了增强主群的勘探能力,提出动态学习榜样策略以保持群体多样性;同时提出随机反向学习机制以实现从群的从全局到局部的自适应搜索功能.在14个不同特征的测试函数上将本文算法与6种知名的BBPSO算法进行对比,仿真结果和统计分析表明本文算法在收敛速度和精度上都有显著提高.
骨干粒子群优化;协作学习;反向学习;多样性
1 引言
粒子群优化(Particle Swarm Optimization,PSO)[1]是一种基于群体的随机优化技术,源于对鸟群,鱼群及人类集体行为的研究.由于PSO概念简洁、易于实现和优良的性能使其在诸多领域的优化问题中得到应用.但是PSO的优化性能和收敛行为依赖学习参数的选择,如惯性权重,加速系数等[2,3].为了提高PSO的优化性能,很多改进策略被提出[4~7].但是在保持算法简洁结构的前提下,同时提高算法的收敛速度和精度仍是PSO一个富有挑战性的问题[8].
2003年,Kennedy提出了一种无参数的骨干粒子群优化[9](BBPSO),该算法采用基于群体最优和个体历史最优信息的高斯采样在解空间中进行搜索.与传统的PSO相比,BBPSO减少了速度项、加速系数、速度阈值等参数,使得算法结构更为简洁易于操作.目前,BBPSO在图像的特征选择,经济调度和故障诊断等实际问题中的应用取得优良的效果[10,11].
由于BBPSO收敛速度快,当解决复杂多峰问题时,群体容易迅速聚集,从而陷入早期收敛.为了提高算法的勘探能力,Krohling等[12]提出了高斯和柯西跳跃策略的BBPSO算法.Orman等[13]将差分算法操作引入BBPSO以增强群体多样性.Zhang等[14]提出了基于突变和交叉策略BBPSO算法以提高粒子的逃逸能力克服早期收敛现象.Riccardo等[15]指出采样方法的微小变化利于 BBPSO在解空间中开拓搜索新的空间.Blackwell[16]对BBPSO做了的群体行为分析,给出了群体坍塌(collapse)条件,提出了跳跃策略的BBPSO算法.Zhang等[17]提出了具有自适应突变的BBPSO算法,并将该算法应用于图像的特征选择.
上述研究表明,突变和跳跃等辅助策略可以增加群体的多样性,但是也降低了算法的收敛速度.为了同时提高算法的收敛速度和精度,本文首先分析了导致BBPSO早期收敛的因素,依据分析结果,提出了并行协作BBPSO (Parallel-Cooperative BBPSO,PCBBPSO).PCBBPSO算法利用两个并行异构种群的协作学习来平衡群体的勘探和开采能力.两个种群分别称为主群和从群.为了增强主群的勘探能力,提出动态学习榜样策略以保持群体多样性;同时提出随机反向学习机制使从群随着进化代数的增加自适应地从全局搜索转向局部搜索.当主群和从群的进化状态满足交互条件时,启动群体间的交互机制,该机制可以提高两群的收敛精度.
2 经典PSO模型
设搜索空间为D维,群体规模为N,粒子i的位置和速度,分别用D维向量表示Xi=(Xi1,Xi2,…, XiD)和Vi=(Vi1, Vi2,…, ViD).第i个粒子迄今为止搜索到的历史最优位置Pi=(Pi1, Pi2,…, PiD),记为Pbest;整个粒子群迄今为止搜索到的最优位置Pg=(Pg1, Pg2,…, PgD),记为Gbest.经典PSO模型中粒子的速度和位置按如下公式更新:
Vi(t+1)=wVi(t)+c1r1(Pi(t)-Xi(t))
+c2r2(Pg(t)-Xi(t))
(1)
Xi(t+1)=Xi(t)+Vi(t+1)
(2)
其中i=1,2,…,N;w为惯性权重,r1和r2为[0,1]之间独立均匀分布的随机数;c1和c2为加速系数.
3 BBPSO算法及其运动行为分析
3.1BBPSO算法
文献[2]指出经典PSO算法中每个粒子收敛于自身个体历史极值和全局极值的加权平均值,即:
(3)
其中φ1和φ2为随机数,分别为φ1= r1c1,φ2=r2c2.依据此结论,Kennedy提出了骨干粒子群优化(BBPSO),算法中没有速度项,粒子i的位置更新方程如下式:
(4)
其中符号N(.)为高斯分布,均值uij=0.5(Pij(t)+Pgj(t)),标准差σij=|Pij(t)-Pgj(t)|, j=1,2,…,D.潘峰等[18]指出经典PSO同BBPSO具有近似的搜索机制.
3.2BBPSO行为分析
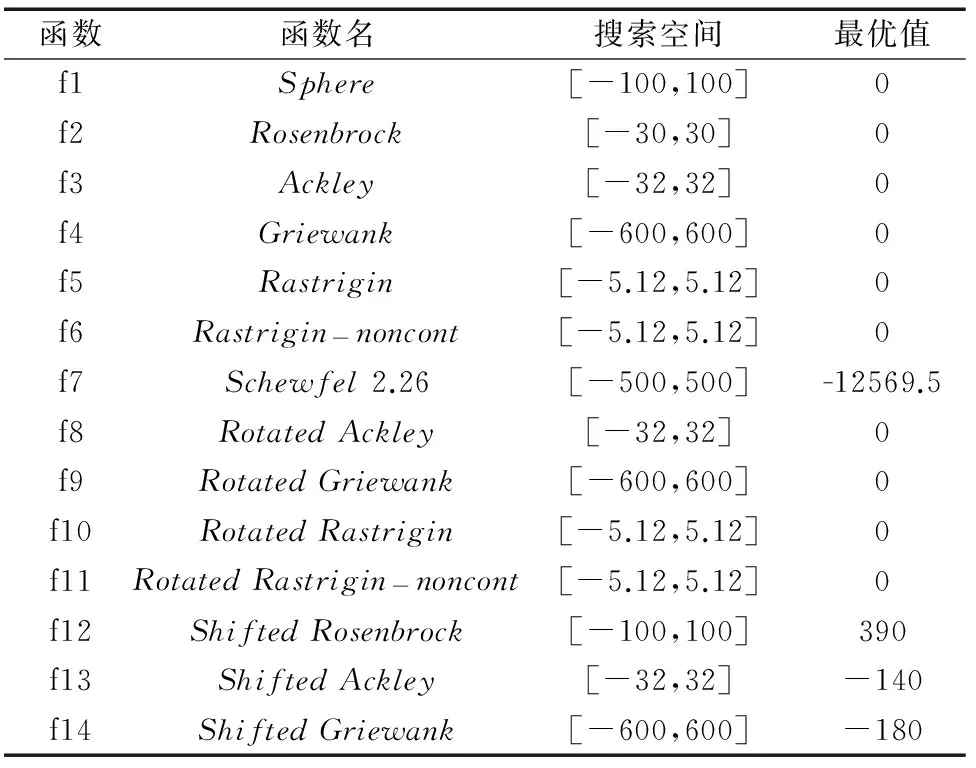
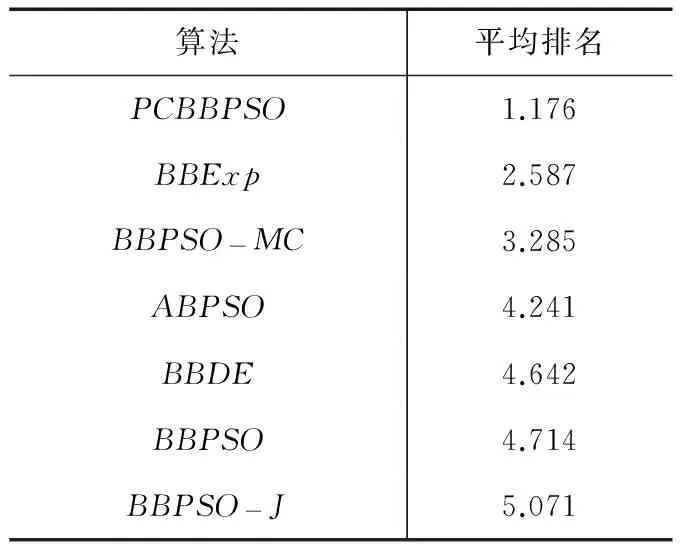
在BBPSO中,粒子的更新位置X(t+1)是个随机变量.为了描述粒子的一维搜索空间,本文引入置信区间的概念,即对一个给定的a(0 由于群体中的粒子均为独立进化,任意选取一个粒子i的运动做分析,得到的结论可以推广至其他粒子.不失一般性,将式(4)简化为一维模型,即 Xi(t+1)=N(0.5(Pi(t)+Pg(t)),|Pi(t)-Pg(t)|2) (5) 依据置信区间的概念,求最短的置信区间是困难的,可转求等尾置信区间. 证明令[θL,θU]为随机变量Xi(t+1)取值的某一区间,并满足P(θL≤Xi(t+1)≤θU)=1-a,将该式变形得 (6) 令c=(θU-ui(t))/σi(t),欲求等尾置信区间,则c=-(θL-ui(t))/σi(t).由式(6)可得式(7), Φ(c)-Φ(1-c)=1-a (7) 由式(7)可解得c=Φ-1(1-a/2).置信下限和上限分别为:θL=ui(t)-σi(t)Φ-1(1-a/2),θU=ui(t)+σi(t)Φ-1(1-a/2). 根据结论1可知,粒子更新位置的置信区间的大小依赖于正态分布的标准差.当置信水平为0.05时,粒子更新位置Xi(t+1)的置信区间为[ui(t)-1.96σi(t),ui(t)+1.96σi(t)],即粒子更新的位置以95%概率将落在这个区间.下面结合图1分析群体陷入早期收敛的原因,图1为一维粒子置信区间示例图,其中置信水平为0.05. 图1中P0和P1分别表示粒子X0和X1的历史最优位置Pbest,Pg表示群体的历史最优位置Gbest,A和B分别是P1和P0与Pg的中心点.点P1,A,Pg,B和P0在数轴上位置分别为(-2,-1,0,3,6).X0和X1在下一次更新且置信水平为0.05的置信区间分别为[-8.76,14.76],[-4.92,2.92].图中虚弧线表示X0的下一次更新的置信区间,实弧线表示X1的下一次更新的置信区间.由图1可知,与P1比较,P0与Pg的距离较远,P0的下一次更新的置信区间较大,表明粒子有较大的搜索空间.在进化初期,粒子的Pbest与Gbest相距较远时,群体具有较强的勘探能力.随着Pbest向Gbest靠近,更新粒子的置信区间随之变小,粒子开始集聚.另外,从图中可以看出,群体中所有更新粒子的置信区间会覆盖Pg附近的区域,使得更新粒子落在这个区域的概率增加,这也是BBPSO快速收敛的重要原因. 4.1主群的学习机制 为了解决群体多样性丧失问题,主群利用动态学习榜样策略来实现全局搜索.动态学习榜样策略是指粒子不再只学习单一的群体最优值Gbest,还可以向其他粒子的历史最优值Pbest学习.如何从多个Pbest中选择自己的学习榜样,本文采用优胜榜样的方法.下面给出优胜榜样的定义. 定义1优胜榜样设群体历史最优个体集合P={P1,…,Pi,…,PN}(i∈1,2,…,N)对于随机变量t,k(t,k∈1,2,…,N,t≠k),有F(Pk)>F(Pt),那么粒子i的第j维优质学习榜样是Pkj. 定义1中的F是适应度函数,适应度值越大代表解越好.优胜榜样是指在每次比较中获胜的Pbest.主群中第i个粒子位置的更新方程为:Xij(t+1)=N(0.5(Pij(t)+Pkj(t)),|Pij(t)-Pkj(t)|2) (8) 4.2从群的学习机制 从群粒子i位置的更新方程为: (9) 式(9)中的Gj按下式生成: Gj(t+1) (10) (11) 4.3交互机制 4.4算法流程 BBPSO算法的算法流程如下: 5.1测试函数和参数设置 为了验证本文算法的优化性能,采用了14个测试函数,包括常规测试函数(f1~f7),带旋转函数(f8~f11)和漂移函数(f12~f14),表1列出了函数的名称,取值范围和最优值.本文算法与传统BBPSO[9]算法及其改进的算法BBExp[9],BBDE[14],BBPSO-MC[15],BBPSO-J[17]和ABPSO[18]进行了实验比较.对比算法的参数设置均参照相应的文献,其中BBDE的重组概率为0.7;BBPSO-MC的突变概率为0.5,方差固定值为0.001,邻域规模为2;BBPSO-J的学习率为0.7.本文设置进化代数为30000代,运行次数为30次,种群规模为40,本文算法中的主群和从群的规模分别为20. 表1 测试函数 5.2评价指标 本文采用适应度均值和方差评价算法的优化性能,其中适应度值为(f(x)-f(x*)) (x*和x分别代表理论最优值和算法获得最优值).为了判断本文算法与6种对比算法的性能是否存在显著性差异,采用wilcoxon rank-sum test检验对结果进行统计分析,显著性水平设为0.05,分别用符号“+”,“-”和“=”表示本文算法的性能要优于,劣于和相当于对比算法.实验结果如表2所示,获得的最优结果用粗体显示. 表2 7种算法在14个测试函数上的均值和方差 5.3算法的收敛精度和速度比较 对于典型测试函数(f1~f7),除了函数f2,本文提出的PCBBPSO均获得最优结果,其中找到了单峰函数f1和多模函数f4~f7理论最优解.对于函数f2,BBPSO获得了最好的结果,PCBBPSO的结果为第三.特别地,对于复杂多模函数(f5~f7),PCBBPSO是唯一可以找到理论解的算法.对于带旋转函数(f8~f10),PCBBPSO获得的结果均明显优于其他6种算法,其中f9函数找到了全局最优解;对于偏移函数(f11~f14),PCBBPSO获得了偏移函数f13和f14的最优结果,并找到了f14的全局最优值.对于f11,PCBBPSO优越于BBExp,BBPSO,BBPSO-J和ABPSO 4种算法.对于偏移函数f12,PCBBPSO获得的结果仅次于BBPSO,优于其他5种算法. 由wilcoxon rank-sum test检验结果可知,PCBBPSO在14个函数上明显优于ABPSO和BBPSO-J.与BBDE,BBPSO-MC,BBPSO和BBExp相比,本文算法分别在12个,8个,10个和9个函数上表现更优.为了综合比较算法之间的性能,本文采用Friedman检验对结果进行分析,表3给出了7种算法的平均排名,本文算法综合性能为第一. 限于篇幅,本文只给出3个测试函数收敛曲线的对比,如图2所示.为便于比较,图中纵坐标为算法获取最优值的对数值.由图2可知,对于多模函数f6,f7和f9,本文算法不仅找到全局最优解而且均在15000代内收敛,说明算法较好地平衡了算法的收敛精度和速度. 表3 7种算法的平均排名 5.4策略分析 PCBBPSO利用动态学习榜样(Dynamic Learning Example,DLE)策略和随机反向学习(Stochastic Opposition-based Learning,SOL)机制协作搜索,其中DLE是实现全局搜索,而SOL是实现全局搜索自适应转向局部搜索.为了研究策略的有效性,将这两个策略分别独立优化表1中的函数,实验结果如表4所示. 由表4可知,对于复杂多模函数f7,f8,f9,f10,f11,f13和f14,DLE比SOL获得了更优的结果,这表明DLE具有全局搜索的能力;对于多模函数f4,f5和f6,DLE和SOL均获得最优值,说明SOL在进化前期具有较强的探测能力,有效地避免早期收敛问题;对于函数f1,f2,f3和f12,与DLE相比,SOL优化的结果具有更高的精度,这表明SOL在进化后期加强了局部搜索.与DLE和SOL的独立优化结果相比,PCBBPSO获得了所有函数的最优结果,表明DLE和SOL协作优化可以更好平衡群体的勘探和利用,展现出满意的整体优化性能. 表4 不同学习策略的比较结果 本文提出了一种并行协作BBPSO(PCBBPSO)算法,采用并行的主群和从群的协调进化以平衡算法的速度和精度.主群利用动态学习榜样策略扩大搜索的区域范围,保持群体多样性;从群通过随机反向学习机制使群体在进化前期提高群体的全局勘探能力,而进化后期增强群体的局部开采能力.通过14个典型函数进行测试,对比结果表明本文算法在解的精度与收敛速度上具有更优的性能. [1 ]Kennedy J,Eberhart R C.Particle swarm optimization[A].Proceedings of the IEEE International Conference on Neural Networks[C].Perth,Australia:IEEE,1995.1942-1948. [2]Bergh F Van den,Engelbrecht A.A convergence proof for the particle swarm optimizer[J].Fundamenta Informaticae,2010,105(4):341-374. [3]Clerc M,Kennedy J.The particle swarm explosion,stability,and convergence in a multidimensional complex space[J].IEEE Transactions on Evolutionary Computation,2002,6 (1):58-73. [4]Ratnaweera A,Halgamuge S,Waston H C.Self-organizing hierarchical particle optimizer with time-varying acceleration coefficients[J].IEEE Transactions on Evolutionary Computation,2004,8 (3):240-255. [5]Zhan Z H,Zhang J,Li Y,Chung H S.Adaptive particle swarm optimization[J].IEEE Transactions on Systems,Man and Cybernetics Part B:Cybernetics,2009,39 (6):1362-1381. [6]Akay B.A study on particle swarm optimization and artificial bee colony algorithms[J].Applied Soft Computing,2013,13(6):3066-3091. [7]周新宇,吴志健,等.一种精英反向学习的粒子群优化算法[J].电子学报,2013,8(41):1647-1652. ZHOU Xin-yu,WU Zhi-jian,et al.Elite opposition-based particle swarm optimization[J].Acta Electronica Sinica,2013,41(8):1647-1652.(in Chinese) [8]Lim W H,Isa N A Mat.Bidirectional teaching and peer-learning particle swarm optimization[J].Information Sciences,2014,280 (10):111-134. [9]Kennedy J.Bare bones particle swarms[A].Proceedings of the IEEE Swarm Intelligence Symposium[C].Indianapolis,USA:IEEE,2003.80-87. [10]Zhang Y,Gong D W,Hu Y,Zhang W Q.Feature selection algorithm based on bare-bones particle swarm optimization[J].Neurocomputing,2015,148(19):150-157. [11]Zhang Y,et al.A bare-bones multi-objective particle swarm optimization algorithm for environmental/economic dispatch[J].Information Sciences,2012,192(1):213-227. [12]Krohling R A,Mendel E.Bare bones particle swarm optimization with Gaussian or Cauchy jumps[A].Proceedings of the IEEE Congress on Evolutionary Computation[C].Trondheim,Norway:IEEE,2009.3285-3291. [13]Omran M G H,Engelbrecht A P,Ayed S.Bare bones differential evolution[J].European Journal of Operational Research,2009,196(1):128-139. [14]Zhang H,Kennedy D D,Rangaiah G P,Bonilla-Petriciolet A.A novel bare-bones particle swarm optimization and its performance for modeling vapor-liquid equilibrium data[J].Fluid Phase Equilibria,2011,301 (1):33-45. [15]Riccardo P,William B L.Markov chain models of bare-bones particle swarm optimizers[A].Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation[C].London,England:ACM,2007.142-149 [16]Blackwell T.A study of collapse in bare bones particle swarm optimization[J].IEEE Trans Evolutionary Computation,2012,16(3):354-375. [17]Zhang Y,Gong D W,Sun X Y,Geng N.Adaptive bare-bones particle swarm optimization algorithm and its convergence analysis[J].Soft Computing,2014,18(7):1337-1352. [18]潘峰,陈杰,等.粒子群优化方法若干特性分析[J].自动化学报,2009,35(7):1010-1015. Pan Feng,Chen Jie,et al.Several characteristics analysis of particle swarm optimizer[J].Acta Automatica Sinica,2009,35(7):1010-1016.(in Chinese) 申元霞(通信作者)女,1979 年生于安徽六安,博士,讲师,研究方向:智能计算、智能信息处理. E-mail:yuanxiashen@163.com 曾传华男,1975年生于重庆,讲师,研究方向:概率与统计理论、偏微分方程数值求解. E-mail:stonezch@163.com 王喜凤女,1980年生于山东成武,讲师,研究方向:信息安全、智能信息处理. E-mail:wxf80106@163.com 汪小燕女,1974年生于安徽桐城,硕士,副教授,研究方向:数据挖掘、粗糙集理论. E-mail:wxyzjx@126.com A Parallel-Cooperative Bare-Bone Particle Swarm Optimization Algorithm SHEN Yuan-xia1,ZENG Chuan-hua2,WANG Xi-feng1,WANG Xiao-yan1 (1.School of Computer Science and Technology,Anhui University of Technology,Maanshan,Anhui 243002,China; 2.School of Mathematics & Physics,Anhui University of Technology,Maanshan,Anhui 243002,China) To deal with the premature convergence of the bare-bone particle swarm optimization (BBPSO) algorithm,we make the analysis of the motion behavior of the particles and point out the reasons leading to the premature convergence.According to the analysis results,a parallel-cooperative BBPSO (PCBBPSO) algorithm is proposed in which the parallel-cooperative learning of a master swarm and a slave swarm balances between exploration and exploitation abilities.In order to improve the exploration ability of the master swarm,a dynamic learning exemplar strategy is presented to preserve the swarm diversity.Meanwhile,a stochastic opposition-based learning mechanism is developed to achieve the abilities of the slave swarm from the global search to the local search.The proposed algorithm was evaluated on 14 benchmark functions with different characteristics.The experimental results and statistic analysis show that the proposed method significantly outperforms six state-of-the-art BBPSO variants in terms of convergence speed and solution accuracy. BBPSO;cooperative learning;opposition-based learning;diversity 2015-04-07; 2015-06-21;责任编辑:覃怀银 国家自然科学基金(No.61300059,No.61472056);安徽高校省级自然科学基金(No.KJ2012Z031,No.KJ2012Z024) TP38 A 0372-2112 (2016)07-1643-06 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.07.018

4 并行协作BBPSO
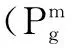
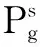
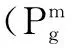

5 数值实验及分析



6 结论


