“再思考”与思维品质的培养

赵丽娟

（庄河市高级中学 辽宁庄河 116400）

“再思考”与思维品质的培养

赵丽娟

（庄河市高级中学 辽宁庄河 116400）

思维能力是数学能力的核心，要提高学生的思维能力，必须重视思维品质的培养。解题能力是数学能力的体现，数学解题过程可分为：“审题”、“分析”、“求解”、“回顾”（即再思考）四个步骤。如果说“审题”是解题的起点，那么解题后的“再思考”便是解题的归宿，它远比前三个步骤更重要。

再思考 思维品质； 培养

“题海”无边，只是解题，解完不去思考研究，只能“食而不知其味”解再多的题也是无法提高能力，也只能被“题海”灌的晕头转向。

以下就几个方面谈谈解题后的“再思考”对学生思维品质的培养。

一、利用对“误解”的“再思考”，培养学生思维的严密性和批判性

在解题过程中，由于各种原因，可能出现这样那样的错误，有些错误极有代表性，通过对这类“误解”的“再思考”，可以加深对概念的理解，对条件的挖掘，对知识间联系的再认识，从而避免错误产生，培养了学生思维的严密性和批判性。

例如，产品检验时，从100件产品中抽3件，如100件产品中有2件次品，抽出的3件中至少有1件是次品的抽法有多少种？

二，利用对“一题多解”的“再思考”，培养学生思维的广阔性和创造性

对同一道题，从不同角度去分析研究，探求多种解题思路，从而得到多种解题方法，使思维的触角伸向不同的方向、不同的层次，有利于培养学生思维的广阔性和创造性。

例如，求sin210°+cos240°+sin210°cos240°的值。

解题后：再思考“可归纳如下：法Ⅰ运用了解决三角求值的一般方法：降幂，积化和差;法Ⅱ运用了代数公式，把平方和转化为和的平方，在化积；法Ⅲ利用式子的对称性构造方程，构造两角和差公式和二倍角公式，体现了方程思想；法Ⅳ联想余弦定理的形式，构造三角形，体现了数形结合思想。这种归纳有利于学生思维的广阔性和创造性的培养。

三、利用对“多题一解”的“再思考”，培养思维的概括性

怎样才能使知识形成网络，得出规律是能力提高的关键。同多“多题一解”找出知识间的联系，得到解题的基本方法，是培养学生思维概括性的有效途径。

给出下列各题：

解完这三道题，可以得到如下方法：研究三角函数问题的第一步必须将化为只含一个角的一个三角函数，即化为的形式，再代换划归为基本函数

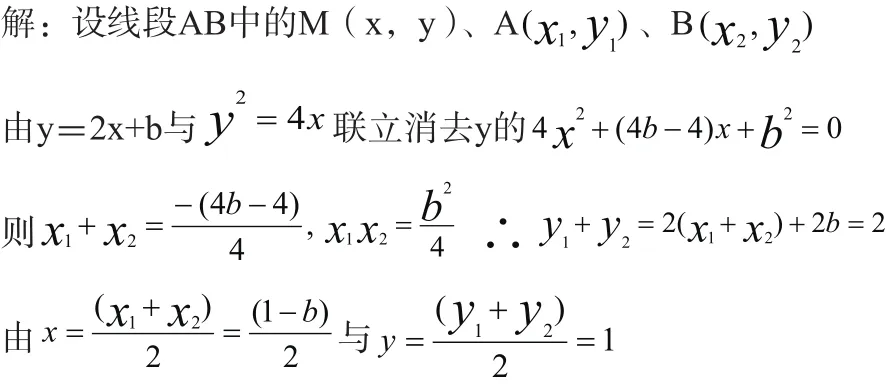
消参数的y=1，……。

其实，对于二次曲线（椭圆、双曲线、抛物线）f(x，y)=0与直线y=kx+b相交于A、B两点，线段AB中点C（x，y），知其几个量求出其它量时均可用上述方法。

象这样的“再思考”，体现了化归思想，培养了学生思维的概括性。

四、利用对“一题多变”的“再思考”，培养学生思维灵活性

数学问题的形式是多样的，怎样才能使学生思维的灵活性得以培养，灵活机智地应付多变的问题呢？通过“一题多变”，对问题进行引伸，是达到这一目的的一个途径。

例如：关于x的方程 x2+(m−3)+m=0（※）有两个实根，求m的范围。

变形：对于方程※，（1）有两个正根，（2）有两个负根，（3）有一正一负根，（4）有两个大于1的根，（5）有一个小于1，一个根大于2，（6）一个根在（0，1）内，另一个根（1，2）内，……，分别求m的范围。

象这样“再思考”题目的变形，把一道题演变为一类题，使学生做一个体会一类题，学一道题会一串题，从而提高学生解决问题的能力，有利于培养学生思维的灵活性，同时也培养了学生思维的深刻性和创造性。