秩亏最小二乘问题的预条件AOR迭代法
沈海龙, 张丽红
(东北大学 理学院, 沈阳 110819)
秩亏最小二乘问题的预条件AOR迭代法
沈海龙, 张丽红
(东北大学 理学院, 沈阳 110819)
秩亏最小二乘问题来源于统计学问题、最优化问题等科学与工程计算领域。由于实际问题所对应的线性方程组的系数矩阵的阶数比较大,且秩亏,换句话说,矩阵A是不可逆的,使其求解变得更为复杂,因此,研究求解秩亏最小二乘问题的高效方法就变得尤为重要。为了求解秩亏最小二乘问题,在预处理基础上提出了二分块的AOR迭代法;研究了新建立的AOR迭代法的收敛性和最优参数的选取,得到了一些相关的定理。数值例子验证了所给方法的可行性。数值实验和理论都表明:新的AOR方法的计算格式更加简单、收敛速度快、并具有广泛的适用性,同时行满秩矩阵A1的选取要比文献[8]中可逆方阵A11的选取更方便。
秩亏损; 最小二乘; SOR方法; AOR方法; BSOR方法
0 引 言
在解决许多应用问题时,往往会遇到如下定义的秩亏最小二问题
‖
其中:A∈Rm×n(m≥n):rank(A)=k 对于最小二乘问题的深入研究,从20世纪60年代才真正开始,而且随着计算机技术和计算机速度的飞速进步,以及科学计算问题的实际需要而有了长足的发展,各种广义的和修正的最小二乘问题的研究方兴未艾。近年来,诸多学者考虑用迭代法来求解秩亏问题。利用迭代法解秩亏最小二乘问题有节省存储空间、减少计算开销等优点,在工程计算中有很重要的应用。因此,寻找秩亏损最小二乘问题的新解法, 即构造更优的迭代格式,使其精确度更高、误差更小、收敛速度加快,更好地应用于实际生产、生活中就具有重要的现实意义。一些学者研究出了适用于系统(1)的迭代方法,具有代表性的如文献[7]通过预处理技术将系数矩阵A分成2块,写成3×3块的增广矩阵。然后用三分块SOR迭代法和二分块SOR迭代法来解决生成的3×3块增广线性方程组,文献[8]沿着文献[7]的思路,研究了用AOR迭代法找系统(1)的解,并且给出了AOR迭代法收敛的一个充分条件。 本文建立了预处理条件的二分块AOR迭代法;研究了预处理条件下的二分块AOR迭代法的收敛性和最优参数的选取,得到了一些相关的定理;然后给出了利用新的AOR迭代法找A+b的定理和推论。数值算例验证了所给方法的可行性和有效性。数值实验和理论都表明:新的AOR迭代法迭代速度快、计算格式简单,并具有广泛的适用性,同时本文中行满秩矩阵A1的选取要比文献[7]中可逆方阵A11的选取更方便。 考虑如下方程 定理1 矩阵Js的特征值在如下区间I:[-βi,0],这里β=‖BC‖2。 定理2Hγ,ω半收敛当且仅当参数γ,ω满足条件 证明 由于Hγ,ω半收敛当且仅当如下3个条件成立: 1) (1-ω)I半收敛; 2)Tγ,ω半收敛; 3) [I-(I-(1-ω)I)(I-(1-ω)I)-1]Rγ,ω[I-(I-Tγ,ω)(I-Tγ,ω)-1]=0。 因为z(x0)是增广系统(3)的解,z(x0)可以写成 本节给出数值例子证明上面的结论和几个相关的问题,在计算中迭代中止的条件为‖Xk+1-Xk‖2<10-4,所有的计算均是在INTELPENTIUM1.8GHZ(256MRAM),Windows7系统下使用Matlab7.0获得的。 例 针对如下方程组,分别用二分块、四分块AOR迭代法求A+b。 方法1 将系数矩阵A分解成二分块,设 由定理4,计算可得ω0=1.4142。 表1 第k步的迭代值Tab.1 The kthstep of iteration value 方法2 将系数矩阵A分解成四分块,设 ‖B‖2=1, 在终止条件‖Xk+1-Xk‖2<10-4下,当γ=0.8时,二分块AOR迭代法在经过有限次迭代后逼近最小二乘解,但是四分块AOR迭代法在300次迭代内是不逼近最小二乘解的。理论跟数值算例都说明将线性方程组的系数矩阵分成二分块要比四分块迭代速度更快、更具普遍性、更方便。 [1]VARGARS.MatrixIterativeAnalysis[M].Prentice-Hall:EnglewoodCliffs, 1962:105-113. [2]YOUNGDM.IterativeSolutionofLargeLinearSystems[M].NewYork:AcademicPress, 1971:150-160. [3]VARGARS,NIETHAMMERW,CAIDY.P-cyclicmatricesandthesymmetricsuccessiveoverrelaxationmethod[J].LinearAlgebraandItsApplications, 1984,58:425-439. [4]MARKHAMTL,PLEMMONSRJ,NEUMANNM.Convergenceofadirect-iterativemethodforlarge-caleleastsquaresproblems[J].LinearAlgebraandItsApplications, 1985,69:155-167. [5]SANTOSCH,SILVABPB,YUANJY.BlockSORmethodsforrank-deficientleastsquaresproblems[J].JournalofComputationalandAppliedMathematics, 1998,100:1-9. [6]MILLERVA,NEUMANNM.Successiveoverrelaxationmethodsforsolvingtherankdeficientleastsquaresproblem[J].LinearAlgebraandItsApplications, 1987,88/89:533-557. [7]TIANH.Accelerateoverrelaxationmethodsforrankdeficientlinearsystems[J].AppliedMathematicsandComputation, 2003,140:485-499. [8]ZHENGB,WANGK.Symmetricsuccessiveoverrelaxationmethodforsolvingtherankdeficientlinearleastsquaresproblem[J].AppliedMathematicsandComputation, 2005,169:1305-1323. [9]魏木生. 广义最小二乘问题的理论和计算[M]. 北京:科学出版社, 2006:30-45. Study of 2-block AOR iterative method for rank deficient least squares problems SHEN Hailong, ZHANG Lihong (College of Science, Northeastern University, Shenyang 110819, China) Rank-deficient least squares problems arise from many scientific and engineering computations such as statistics, optimal problem and so on. In the practical problems, since the order number of corresponding coefficient matrix of linear equations is larger, and the rank of matrix is a deficit. In other words, matrixAis irreversible. Then solving process is become more complex. So it is very important to study of the suitable iterative methods for rank-deficient least squares problems. For solving the least square problems with rank-deficient, the 2-block AOR method by preconditioning technique was given. The convergence analysis of the new AOR method and the choice of optimal relaxation parameters were studied. The corresponding theorems were gotten. Numerical examples showed the effectiveness of new method. It suggests that the new iterative AOR method is simpler, faster in convergence speed, more extensive applicability than the method in [8]. Meanwhile, matrixA1is full row rank, it is more convenient than the requirement ofA11in [18]. rank deficient; least squares; SOR method; AOR method; BSOR method 2016-01-03。 国家自然科学基金资助项目(11071033); 中央高校基本业务费资助项目(090405013)。 沈海龙(1971-),男(朝鲜族),吉林延边人,东北大学讲师,博士。 1673-5862(2016)03-0333-05 O241.2 A 10.3969/ j.issn.1673-5862.2016.03.0171 二分块AOR迭代法的格式及收敛性




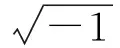

2 用AOR迭代法找A+b

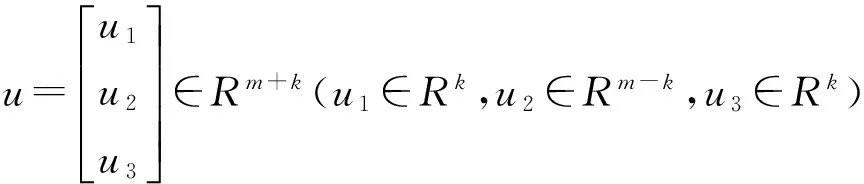
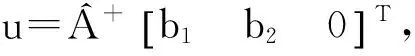
3 数值算例

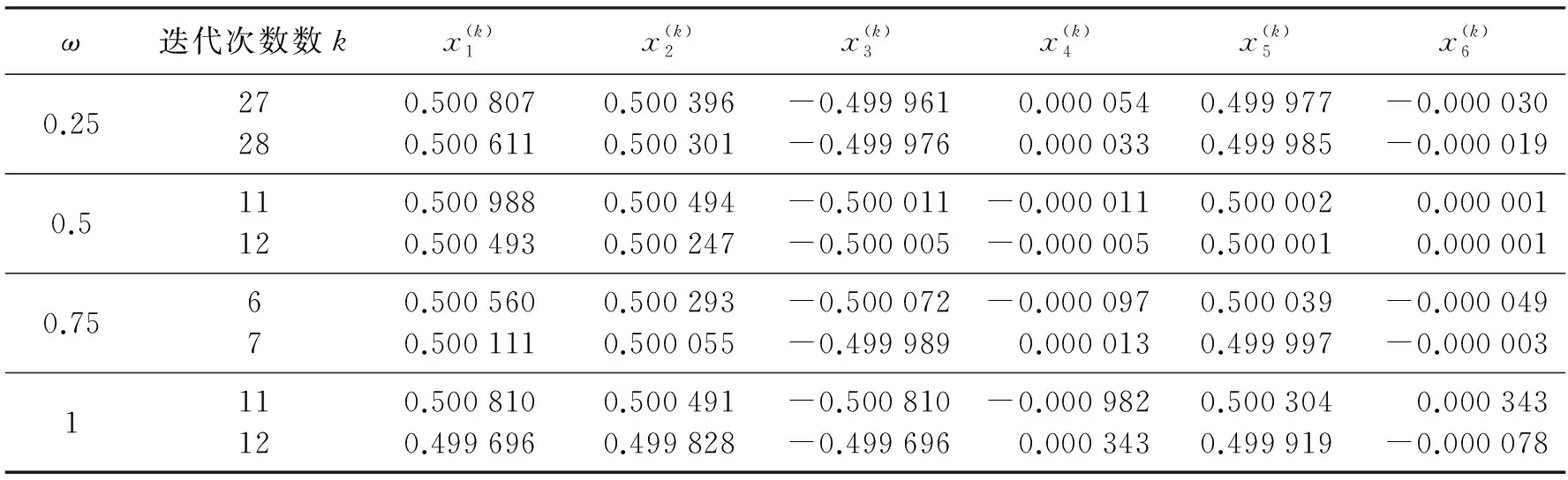


4 结 论

