血管外给药单室模型的最优控制
刘爱红, 杨 光
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
血管外给药单室模型的最优控制
刘爱红, 杨 光
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
考虑血管外给药单室模型的脉冲最优控制问题。首先,利用脉冲微分方程和常微分方程重新改写传统的血管外给药微分方程模型,从而既突出给药这一脉冲过程,又将一次给药模型推广为周期性多次给药模型;然后,求解新建立的脉冲微分方程,进而确定每次给药后吸收部位药量和体内药量的表达式;接下来,利用一阶和二阶导数推导出每次给药后药量的变化规律和药量与给药次数之间的内在联系,并给出一个疗程内体内药量的最高值与最低值;再次,构建描述体内药量积蓄程度的目标函数,利用最优化方法,确定最佳给药次数、时间间隔和剂量,使得药物在体内的积蓄最少,对人体的伤害最小;最后,Matlab仿真结果表明该方法有效、可行。
单室; 血管外给药; 药量; 给药方案; 脉冲微分方程; 最优控制
药物动力学是一门药效学与数学有效结合的交叉学科,模型的建立与给药方案的设计一直是其研究的主要内容之一,到目前为止,有大量的相关文献。对于单室血管外给药模型,在模型建立方面,大多数都建立了如下的微分方程模型:
其中:Xa为吸收部位可吸收的药量;X为体内的药量。这个模型有一定的局限性。首先,这个模型不能直观的反映出周期性给药方式下的药量变化;其次,此模型仅体现了给药后药量变化的连续性,却未能体现给药这一行为的特点。在给药方案设计方面,少有文献将最优化方法与积蓄药量对肝肾等器官的伤害程度结合在一起共同去确定最佳给药方案。因此,本文将在模型建立和给药方案设计这两方面进行大胆的尝试研究。
首先,本文考虑周期性给药模式,运用脉冲微分方程改写传统的单室血管外给药微分方程模型;其次,计算出一个疗程内体内的最高、最低药量;然后,运用最优化理论,确定使得体内积蓄药量最少,对人体害程度最小的最佳给药间隔与给药量;最后,通过仿真模拟证明本文建立模型的有效性。
1 血管外给药单室模型的建立
本文给出如下假设:
[H1] 给药是一个脉冲过程,首次给药量为x0,维持给药量为I;
[H2] 给药的时间间隔恒为τ,1 d内的给药次数为n,1 d的给药次数不会超过5,否则太过繁琐,即n≤5且n∈N,nτ=24。
[H3] 药量在人体内积蓄程度用体内药量在给药时间内的积分来表示;
[H4] 吸收部位可吸收药量的变化为τ-周期解,F为生物利用度,从第2次给药开始,每次给药后吸收部位药量均为首次给药量,则
Xa((i-1)τ-0)+FI=Fx0,i=2,3,…。
[H5] 中毒临界值hmax与药效临界值hmin均是已知的常数。
[H6] 本文考虑短期给药且一个疗程为6 d,即144 h。
依据上述假设,可得新模型:
由式(2)前4项可得
由[H4]和式(3)可得
注1 根据[H4]及式(3),易得第i次给药后吸收部位可吸收药量的表达式为
2 最佳给药策略的确定
最佳给药方案使体内药量在一个疗程内积蓄最小,并且从第2次给药时刻起体内药量均在药效临界值与中毒临界值之间。首先确定每次给药后体内药量的表达式,然后根据最优化方法给出最佳给药方案的最优化模型。
定理1 对于血管外给药模型(2),在一个疗程,即在[0,144]内,第i次给药后体内药量的表达式为
其中:(i-1)τ≤t≤iτ,i=1,2,…,6n;nτ=24。
证明 第1次给药后体内药量的表达式(4)式已给出。第2次给药后,体内药量的初值为
等价于求解如下微分方程:
即

同理可得第i次给药后体内药量的表达式为式(7)。
定理2 在整个疗程内,体内最高药量为最后一次给药期间的最高药量,且为
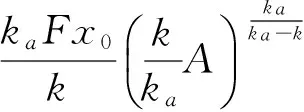

证明 令θ=t-(i-1)τ, (i-1)τ≤t≤iτ,i=1,2,…,6n,nτ=24, 0≤θ≤τ。
则第i次给药后体内药量的表达式(7)变为
由于
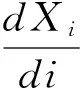
因此,∀θ, 0≤θ≤τ,i次给药后体内药量随着i增大而增大。
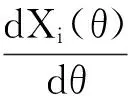
θ*
由于
所以当θ满足式(11)时,此时刻药量为第i次给药后体内最高药量。综上可知,最后一次给药后体内药量X6n(t)的最高值即为是整个疗程体内最高药量,即为(9)。
注2 为了使药物达到药效且不对人体造成中毒,要求第2次给药在τ时刻的药量与体内最高药量均在药效临界值与中毒临界值之间,即满足下列条件即可
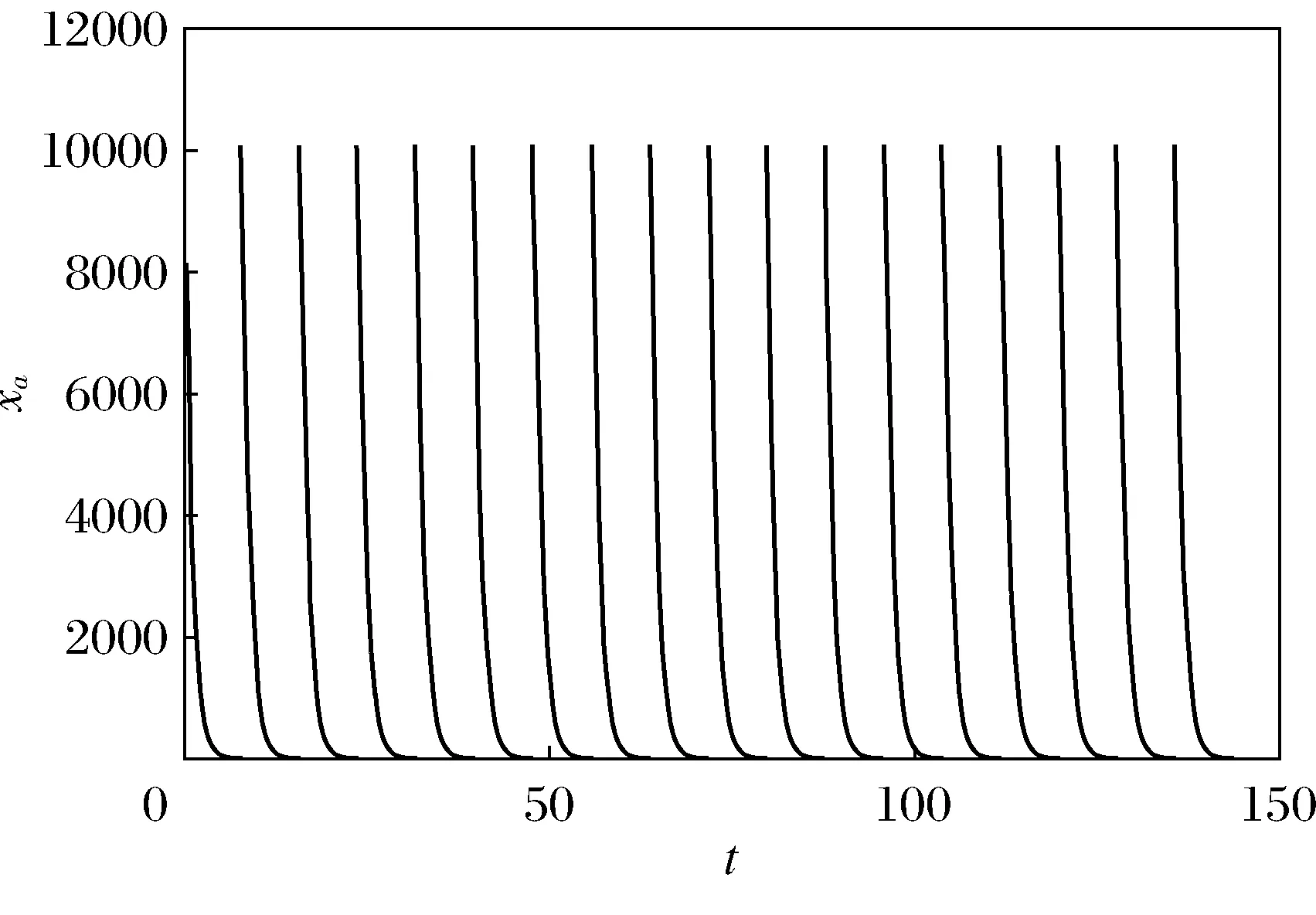
hmin 定理3 在一个疗程内,体内药物的积蓄f为 证明 由[H3]、式(10)易得。 且最佳给药间隔τ*及维持给药量I*为 设有某种药物ka=1h-1,k=0.1h-1,hmin=5 000 μg,hmax=50 000μg,F=0.8,将数据带入上述最优化模型中,运用Matlab软件求解可得 此时,一个疗程内吸收部位与体内药量的变化图像如图1、图2所示。图1说明给药确实是一个脉冲过程,且吸收部位药量的变化是周期的。此外,如此的给药方式保证了体内药量积蓄最小,且每次给药后的药量都在药效之上,中毒临界值之下,这符合最佳给药策略的期望,模型有效可行。 图1 吸收部位药量变化Fig.1 Variety of dose in absorption site 图2 体内药量变化Fig.2 Variety of dose in vivo 本文在周期性给药的前提下,结合脉冲微分方程和常微分方程建立了新的血管外给药单室模型,突出了给药的脉冲过程,将一次给药模型拓展为周期性多次给药模型。另外,考虑了药量在体内的积蓄程度,运用最优化理论,构造了给药方案设计的最优控制模型,确定的最佳给药间隔、给药量使得药物在体内的积蓄最小,对人体的伤还最小。Matlab仿真结果证明了方案的科学可行性。 [ 1 ]梁文权. 生物药剂学与药物动力学[M]. 北京:人民卫生出版社, 2007. [ 2 ]杨光,刘爱红,王爽. 单室模型的最佳给药方案[J]. 沈阳师范大学学报(自然科学版), 2015,33(3):337-340. [ 3 ]杨光. 害虫综合治理模型与最优控制策略[J]. 沈阳师范大学学报(自然科学版), 2011,29(4):482-485. [ 4 ]薛定宇,陈阳泉. 基于MATLAB/Simulink的系统仿真技术与应用[M]. 北京:清华大学出版社, 2002. [ 5 ]段春林. 临床给药方案探讨[J]. 中国现代药物应用, 2010,4(2):163. [ 6 ]汝玲. 临床药师参与个体化给药方案设计的临床实践与案例分析[J]. 中国医院用药评价与分析, 2013,13(3):273-276. [ 7 ]杨进波. 创新性药物临床试验剂量和给药方案的探索与确定[J]. 中国临床药理学与治疗学, 2008,13(8):841-846. [ 8 ]刘昌孝. 我国药物动力学研究50年发展概述[J]. 天津中医药大学学报, 2008,27(3):127-134. [ 9 ]李琳. 浅谈给药方案设计[J]. 中国继续医学教育, 2015,7(3):218. [10]杨庆之. 最优化方法[M]. 北京:科学出版社, 2015. Optimal control for one-compartment extravascular administration model LIU Aihong, YANG Guang (College of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China) This paper considers the issue of impulsive optimal control for one-compartment extravascular administration model. Initially, impulsive differential equations and ordinary differential equations are used to rewrite the traditional extravascular administration differential equation model so as to highlight the impulsive process of dosing and promote the once dosing model to periodic dosing model. Furthemore, expressions of doses in vivo and absorption site after each dosing are determined by solving the fresh impulsive differential equation. The varying pattern of dose and the inner relationship between dose and number of dosing are obtained by the first and second order derivates, and the highest and lowest doses of drugs during a course of treatment are given. Additionally, a target function which describes the accumulation extent of drugs in vivo is constructed, the best dosing numbers, time interval and doses are obtained by optimization methods, which makes the accumulation extent of drugs in vivo minimum as well as brings the least harm to human body. Finally, the simulation result operated by Matlab shows the validity and feasibility of the proposed method. one-compartment; extravascular administration; dose; dosing strategy; impulsive differential equations; optimal control 2016-03-02。 辽宁省科技厅自然科学基金资助项目(2014020120)。 刘爱红(1990-),女,辽宁北票人,沈阳师范大学硕士研究生; 杨 光(1964-),女,辽宁抚顺人,沈阳师范大学教授,博士。 1673-5862(2016)03-0287-04 O232 A 10.3969/ j.issn.1673-5862.2016.03.007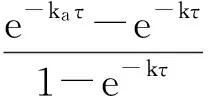

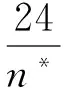
3 仿真与讨论


4 结 论

