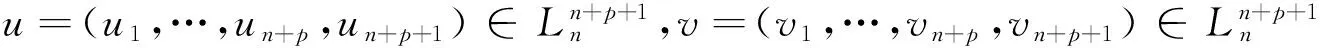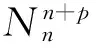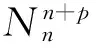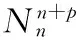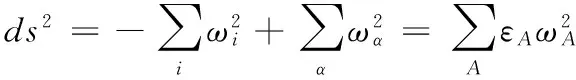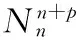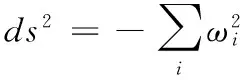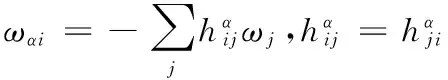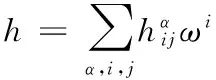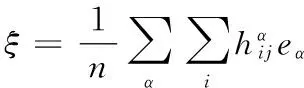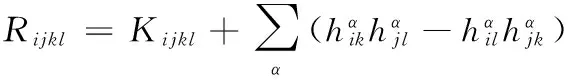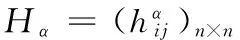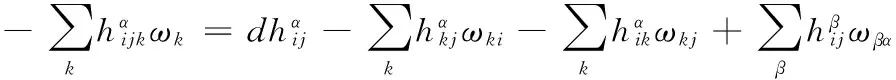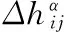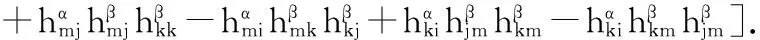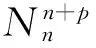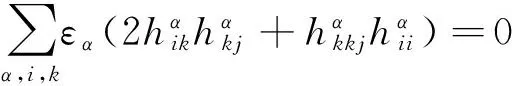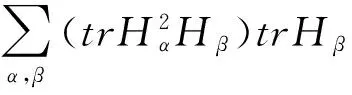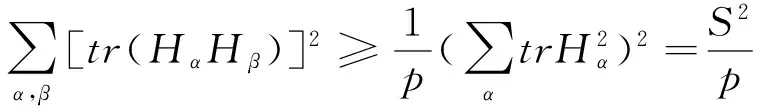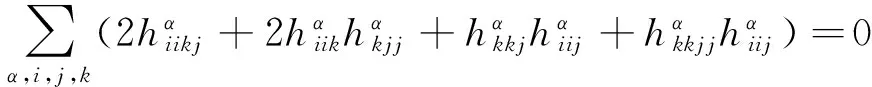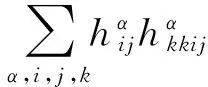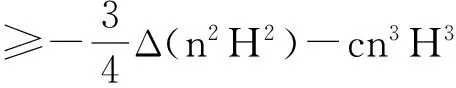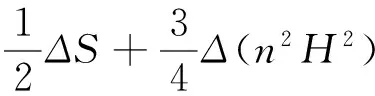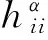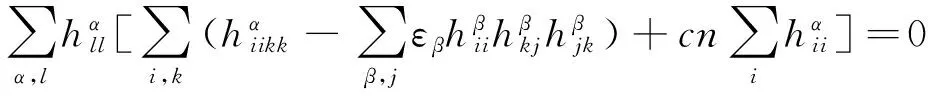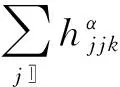de Sitter空间中的紧致2-调和类时子流形

李　影，　宋卫东

(安徽师范大学 数学计算机科学学院，安徽 芜湖　241000)



de Sitter空间中的紧致2-调和类时子流形

李影，宋卫东

(安徽师范大学 数学计算机科学学院，安徽 芜湖241000)

摘要：利用活动标架法，得到了de Sitter空间中的紧致2-调和类时子流形的一个积分不等式以及该子流形成为极大类时子流形的关于其第二基本形式模长平方一个拼挤定理.

关键词：de Sitter空间；2-调和映射；类时子流形

按照J. Eells和L. Lemmaire在文献[1]中的设想，姜国英在文献[2，3]中讨论了黎曼流形间的2-调和映照，欧阳崇珍在文献[4]中讨论了黎曼流形M到伪黎曼流形N的2-调和等距浸入，得到这种等距浸入是2-调和映照的充要条件以及伪黎曼空间型的2-调和类空子流形的Pinching现象.从相对论的角度来说，伪黎曼流形的子流形或许比黎曼流形的子流形更有意义，它们在研究方面有很多类似的地方，但是也有很多不同之处.对于de Sitter空间中的类空子流形，目前已有许多研究结果.文献[5]将de Sitter空间中的子流形分为类空、类时、类光子流形.文献[6]给出了de Sitter空间中2-调和类空子流形的一个积分不等式及其Pinching现象.本文仿照其方法，建立了这类空间中2-调和类时子流形的一个积分不等式以及该子流形成为极大类时子流形的关于其第二基本形式模长平方一个拼挤定理.具体结果如下：

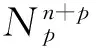
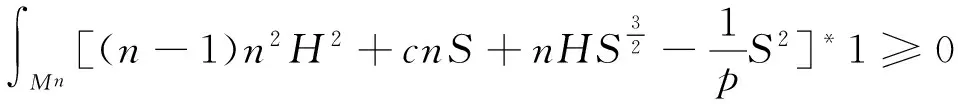
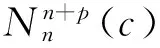
S

则Mn是极大的.

1预备知识

本文约定各类指标取值范围

1≤A,B,C,…,≤n+p;1≤i,j,k,…,≤n;n+1≤α,β，γ，…,≤n+p.

设Ln+p+1是n+p+1维实向量空间Rn+p+1并赋予内积

=-δij,=0,=δαβ，

KABCD=εAεBc(δACδBD-δADδBC).

(1)

(2)

(3)

其中h,ξ,Rijkl,Rαβkl分别是Mn的第二基本形式，平均曲率向量，曲率张量，法曲率张量.

定义

结合(1)式，则有

(4)

(5)

在此需要如下引理：

(7)

(8)

2定理证明

定理1的证明

由(6)式可知，

(9)

因此，

(10)

由柯西不等式得

(11)

另外，由文献[6]，有

(12)

(13)

对(7)式求共变导数并求和可得

对上式调整指标，再利用(8)式有

(14)

结合(11)-(14)式，则有

由于Mn是紧致无边的，根据Stocks定理，对上式两边积分即得定理1的证明.

定理2的证明

≥-n2H2S+cn3H2=n2H2(-S+cn).

所以，当S0时，能得到H=0，即Mn是极大类时子流形.因此，定理2得到证明.

参考文献：

[1]EELLS J, LEMAIREL. Selected topics in harmomic maps[J]. CBMS 50, AMS, 1983.

[2]姜国英.Riemmann流形间的2-调和映照及其第一、第二变分公式[J].数学年刊，1986，7A：389-402.

[3]姜国英.Riemann流形间的2-调和等距浸入[J].数学年刊，1986，7A：130-144.

[4]欧阳崇珍.伪黎曼空间型的2-调和类空子流形[J].数学年刊，2000，21A：649-654.

[5]刘海明，苗佳晶，许宏文，葛礼峡.广义De Sitter空间中的类时超曲面[J].数学的实践与认识，2011，41(16)：193-200.

[6]舒世昌，刘三阳.de Ditter空间中的2-调和类空子流形[J].工程数学学报，2003，20(1)：135-138.

[7]孔令令，裴东河.四维Minkowski空间中类时超曲面的de Sitter Gauss映射的奇点分类[J].中国科学A辑：数学，2007，37(6)：751-758.

[8]沈一兵.关于伪Riemmann流形的极大子流形[J].杭州大学学报，1991，18(4)：371-376.

[9]高真圣，欧阳崇珍.局部对称伪黎曼流形中的2-调和类空子流形[J].南昌大学学报，2004，28(1)：12-16.

[10]宋卫东，江桔丽.关于局部对称伪黎曼流形中的2-调和类空子流形[J].系统科学与科学，2007，27(2)：170-176.

[11]胡有婧，纪永强.de Sitter空间中的紧致极大类时子流形[J].吉林大学学报，2014，52(5)：895-900.

DOI：10.14182/J.cnki.1001-2443.2016.04.006

收稿日期：2015-06-20

基金项目：国家自然科学基金(11071005)；安徽师范大学研究生科研创新与实践项目(2015cxsj108zd).

作者简介：李影(1991-)，女，安徽阜阳人，硕士研究生，主要从事微分几何研究.通讯作者：宋卫东(1958-)，男，安徽桐城人，教授，主要从事微分几何研究.

中图分类号：0186.12

文献标志码：A

文章编号：1001-2443(2016)04-0338-04

The Compact 2-Harmonic Timelike Submanifolds in a de Sitter Space

LI Ying,SONG Wei-dong

(College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000, China)

Abstract:Based on the moving frames, an integral inequality about compact 2-harmonic timelike submanifolds was obtained in a de Sitter space and a pinching theorem about the squared norm of the second fundamental form for the compact 2-harmoinc timelike submanifold in a de Sitter space was given.

Key words:de Sitter space; 2-barmonic map; timelike submanifold

引用格式：李影，宋卫东.de Sitter空间中的紧致2-调和类时子流形.安徽师范大学学报：自然科学版，2015，38(5)：338-341.