振荡周期不受温度影响的生物调控网络的数值研究

王宏利，　吴丽莉

(北京大学 物理学院，北京　100871)



振荡周期不受温度影响的生物调控网络的数值研究

王宏利，吴丽莉

(北京大学 物理学院，北京100871)

摘要：生物学中普遍存在的生物钟的基本特性之一是其振荡周期不随环境温度变化而变化，即具有温度补偿特性，其机制是近年来研究的热点.本文对具有振荡周期不随温度变化的基因调控网络做了数值分析.温度补偿振荡是一种系统水平的性质，跟网络的拓扑结构具有密切联系.对多节点的仅有抑制性调控关系的随机网络的计算表明，温度补偿的振荡行为可以仅仅通过采用适当的拓扑结构实现，而不需要细调的动力学参数.对所有3个节点网络的穷举发现，温度补偿振荡网络结构上是两种性质互补的振荡网络模体的组合，即延迟的负反馈网络)、抑制子振子和激活抑制振子、底物耗尽振子的组合.对网络振荡周期随参数的敏感性分析表明，温度补偿振荡可以通过熔断机制来实现，振荡周期仅敏感依赖于极少数的反应速率常数，而这些常数的活化能很小因为阻断了温度对振荡周期的影响.

关键词：鲁棒性；振荡；生物网络

自发周期振荡作为一种典型的非线性动力学行为广泛存在于各类动力学系统中.在生物体系中，生命活动一般表现为日夜节律的振荡形式即生物钟，其周期等于地球自转周期(24小时).生物钟是生物系统与其生存的地球环境日夜轮转相适应的结果，普遍存在于从简单的单细胞生物(如蓝藻)到鸟类以及人类等高等哺乳动物[1].生物钟最重要的特性之一是随着环境温度的显著变化，振荡周期不发生明显改变.振荡周期不随温度的变化而变化的特性被称为温度补偿[2].从亚细胞水平看，生物钟行为是相关基因以及蛋白分子之间相互作用和调控的结果，其基础是生化反应.生化反应速率常数一并地随着温度升高而加快.随温度的升高和反应速率的加快，生物钟的振荡周期不缩短反而在一定温度范围内保持恒定，其温度补偿的机制一直是生物物理研究中一个悬而未决的问题.在过去的二十多年中，研究者们在多种模式生物的生物钟分子相互作用基础上，提出了多种温度补偿机制，如拮抗平衡机制[3]，开关机制[4]，单一酶催化的化学反应机制[5]，以及最近提出的将温度补偿看成是周期对温度变化的适应性机制[6].这些研究均在一定程度上说明了实现温度补偿的可能途径，同时表明，温度补偿是系统的整体的特性，与其分子相互作用的网络结构具有一定关系.

本文试图寻找具有温度补偿的振荡网络的拓扑结构上的特点，发掘具有振荡和温度补偿双重特性的生物基因调控网络的简单结构和设计原理.我们考虑了由若干个节点构成的基因调控网络，通过枚举的方法寻找能实现振荡同时又具有周期不随温度变化特性的网络，通过分析其网络结构上的特点，寻找能实现温度补偿振荡的网络结构上的规律.我们发现，动力学单一的结构多节点网络，只要结构合适都可以形成具有周期随参数变化不敏感的温度补偿振荡.少节点的简单网络则需要适当的结构和参数配合才能形成温度补偿振荡.对于不多于三个节点的基因调控网络，有四种基本的网络模体(motif)，即延迟的负反馈振子，三节点抑制子振子，激活抑制振子和底物耗尽振子.该四种简单结构的组合即可形成具有稳健温度补偿的振荡行为.

1抑制相互作用网络中的温度补偿振荡

我们首先考虑多节点的抑制相互作用网络是否具有实现温度补偿振荡的可能性.网络中的每个节点表示一个基因的蛋白表达产物，网络节点之间仅有抑制相互作用，即一个基因表达出的蛋白质产物对另一个基因的转录具有抑制作用.为排除参数取值不同的影响，网络中所有的抑制相互作用都相同，网络中的某个节点i满足的动力学方程为[7]：

(1)

方程右侧第一项为网络相互作用对节点i表达速率的贡献，第二项为蛋白酶引起的降解；矩阵元Aij表示网络节点j到i的连接矩阵，可取值1(激活)，-1(抑制)和0(没有相互作用).分母中Aij(xj)n的将引起基因i表达速率的抑制.参数I表示抑制的强度.由于温度变化10摄氏度，反应速率常数一般变为原来的2倍.在我们的数值研究中，温度的变化表现在I取值的变化上，I∈[1,2].为了寻找在温度突变的条件下能保持振荡周期不变的网络结构，我们首先尝试了10个节点20条节点连接的网络.通过初始的随机网络，检查其是否能振荡；对于能振荡的网络，则检查是否具有I变化下的稳定周期.如果能振荡但周期不稳定，则调整其网络节点的连接，使一条边随机地指向其他的节点，通过不断的网络结构的演化，寻找温度补偿的振荡网络结构.对10个节点20条边的网络的计算表明，从任意一个初始的网络出发，都可以在有限的演化步骤之后到达能实现温度补偿的振荡结构.图1a所示为一个初始的随机网络结构和演化得到的图1b所示的具有温度补偿的振荡网络结构.

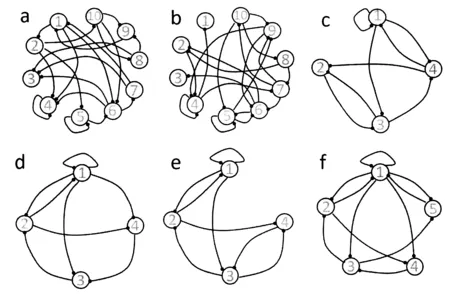
图1　网络演化得到的温度补偿网络.(a) 10个节点20条边的初始振荡网络；(b)以网络(a)为起点演化得到的温度补偿振荡网络；(c)(d)(e)为演化得到的4个节点8条边构成的温度补偿振荡网络；(f)5个节点和11条边构成的温度补偿网络.计算过程中，方程1中的参数p=100,n=3.

以上没有可调参数的10节点网络中，只要调整网络结构就可以进化出具有振荡周期不随温度变化的网络.这表明，温度补偿振荡网络可以仅仅通过适当的网络拓扑实现.接下来，我们把网络的节点数降到3，4和5，分别检查了网络的边数由最少(分别为3，4，5)到最多(分别为9，16，和25)，依然通过进化的算法通过结构的调整寻找温度补偿网络.对于3节点网络，不论边数，仅有首尾互相抑制结构(即repressilator, 结构为)具有振荡行为，但周期会随I的变化显著改变.对于4节点网络，我们穷举了所有可能的边数和连接方式，发现有3个结构可以实现温度补偿振荡(如图1c，d，e所示).5节点网络中能实现温度补偿的网络结构比4节点网络多，图1f展示了其中的一个.以上结果表明，温度补偿振荡网络可以在相对简单的网络中出现.

2温度补偿振荡网络的设计原理

在以上的分析中，我们仅仅考虑了抑制相互作用的多节点网络，且数学模型中没有可以自由调整的参数.为了寻找能实现温度补偿的最简单的振荡网络，弄清楚补偿振荡网络的构成原理，我们接下来考虑仅有3节点构成的简单网络.不同于抑制相互作用网络，节点(基因)间可以互相抑制也可以互相激励.如果有一个基因的表达受到多于一种基因的蛋白表达物的调控，则它们将以竞争的方式结合到该基因的启动子上.在模型中考虑了基础表达和线性降解项后，网络中一个基因的蛋白表达速率可以通过如下形式的常微分方程组描述[7]:

(2)

其中xi为基因i表达出来的蛋白质分子的浓度，Kij为解离常数,n为希尔系数，最大表达速率vij及降解速率常数ri被假定为依赖于温度，遵守阿仑尼乌斯方程：

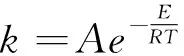
(3)

上式中E表示活化能，T为开尔文温度，R为气体常数.Jil为网络的连接矩阵.我们假定δi和Kij不随温度变化.文献报道的结果表明蛋白质的合成以复杂的形式依赖于温度.上述反应参数随温度的变化关系是我们的模型假设，是对实际情况的简化.由于网络中仅有三个节点，温度补偿的振荡行为需要适当的网络结构和适当取值的参数的结合.我们枚举了每一种3节点的网络结构，每个网络结构通过拉丁超立方采样的算法产生10000组参数[8]，检验每组参数下动力学系统是否具有温度补偿的振荡行为.对于可以振荡的网络，进一步调整温度使其在区间[283K，293K]内变化.通过计算不同温度下的振荡周期，检验其是否具有不随温度改变的振荡周期.对于一个网络结构可能存在多组参数实现补偿振荡.图2所示为3节点网络枚举温度补偿振荡的算法流程图.为了衡量一个网络结构实现补偿振荡和补偿振荡的能力，分别采用了Q-值和q-值来估计.Q-值为一个网络结构的10000组随机参数中能产生振荡的参数的数目；q-值则进一步表示Q组参数中有多少组参数可以实现温度补偿的振荡.

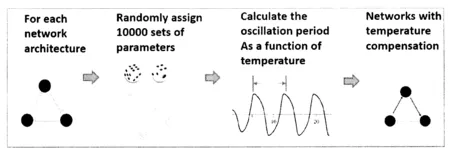
图2　枚举3节点网络结构通过在参数空间中用拉丁超立方采样参数筛选温度补偿振荡网络算法流程图

从所有可能的2423个结构上不等价的3节点网络结构中，计算共筛选出具有温度补偿的振荡网络结构787个.这些网络中具有最少边数的最简网络共发现有四种，如图3b中的M1, M2, M3和M4所示.这些最小网络恰好是目前发现的能实现振荡的最简单模体(motif)，它们分别被称为延迟的负反馈振子(M1)，三节点抑制子振子(M2)，激活抑制振子(M3)和底物耗尽振子(M4).对787个网络结构的分析表明，这些能实现温度补偿振荡的网络中绝大多数都包含这4种基本振荡模体或它们的组合.图3c所示为这些最简单模体组合的三个实际例子.为了弄清4个基本振荡网络结构的差异，我们对它们的参数空间进行了更大规模(100000组)的参数采样，通过统计它们的Q-值和q-值，并比较它们在振荡能力和实现温度补偿能力上的差异.结果表明，模体M1，模体M2和模体M3，模体M4在振荡能力上差异很大，前两者的Q-值比后两者大很多，表明M1和M2两种结构对于网络实现振荡的功能具有很大优势.另一方面，模体M3和模体M4虽然不容易振荡，但是它们具有相对较大的q-值，表明它们虽然不容易产生振荡，但是发生振荡后其周期抵抗温度变化的能力比模体M1和模体M2要强很多.这提示我们，具有稳健实现温度补偿的振荡网络可以通过这两类在实现振荡和实现温度补偿的能力上互补的基本网络的组合构成.对温度补偿振荡能力最强的35个网络的分析表明，它们确实是通过这两类模体的组合构成了.图3c所示的3个网络结构即为q-值最大的能实现温度补偿的结构之一.

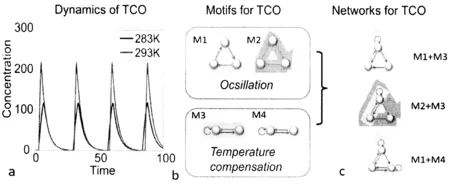
图3　实现温度补偿振荡的最简单网络，延迟的负反馈振子M1(delayed negative feedback)，抑制子振子M2(repressilator)，激活抑制振子M3(activator-inhibitor)和底物耗尽振子M4(substrate-depletion).图中的TCO表示温度补偿振荡.(a)温度补偿示意图；(b)四种最简单的振荡模体(motif)；(c)4种模体组合形成稳健温度补偿振荡网络的3个实例.

3三节点温度补偿振荡网络的机理分析

为了检查以上计算得到的温度补偿振荡网络实现补偿振荡的机制，我们对q-值最大的35个网络进一步分析了其振荡周期对参数以及温度的敏感性.由于假定了反应速率常数以阿仑尼乌斯方程(3)的方式依赖于温度，则温度补偿振荡从数学上可以表示为不同参数的改变对周期影响的拮抗平衡[10]，即：

(4)

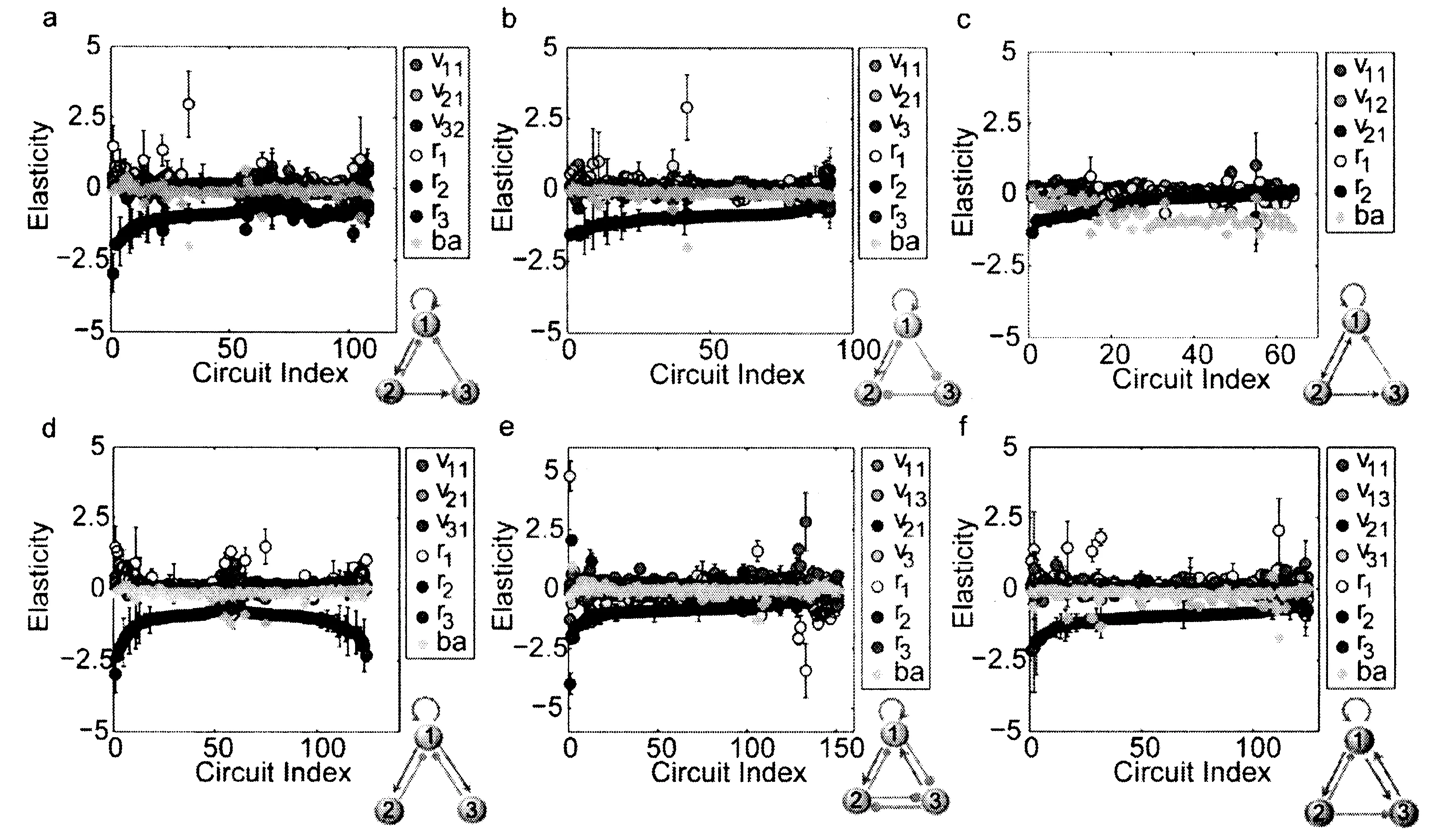
图4　六种温度补偿网络结构的反应速率常数在补偿振荡常数下对振荡周期的弹性(在温度变化区间取平均值).横坐标表示实现补偿振荡的不同常数.图中的灰色小圆表示所有常数弹性的叠加.

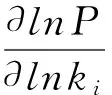
4结论

以上对能实现周期不随温度变化的振荡网络，从多节点到少节点都做了较为系统的检验.对多节点的分析表明，温度补偿的振荡行为，可以仅仅通过合适的网络结构来实现，而不需要调整系统动力学中的参数.说明温度补偿振荡行为主要是一种系统水平的性质，跟网络的拓扑结构密切相关.对仅有3个节点的网络的枚举表明，温度补偿振荡可以通过合适的网络结构和适当的参数的组合来实现.在网络结构上，温度补偿振荡网络可以通过两种性质互补的振荡网络模体的组合来实现，即延迟的负反馈网络(M1)、抑制子振子(M2)和激活抑制振子(M3)、底物耗尽振子(M4)的组合.对于温度补偿网络的振荡周期对参数的敏感性的计算表明，温度补偿振荡可以通过熔断机制来实现周期对温度的鲁棒性.网络的结构在一定程度上决定了系统整体的振荡周期仅敏感依赖于极少数的参数，而这些参数可以通过采用很小的活化能的方式阻断温度升高导致反应速率加快引起的振荡周期的缩短.虽然系统中的大多数参数受温度的影响可以显著加快，但是由于它们的变化对振荡周期的影响不明显，最终导致了具有温度补偿的振荡行为.

参考文献：

[1]Eckel-Mahan K and Sassone-Corsi P. Metabolism and the circadian clock converge[J]. Physiol Rev, 2013,93(1):107.

[2]HASTINGS J W， SWEENEY B M. On the mechanism of temperature independence in a biological clock[J]. Proc Natl Acad Sci USA, 1957,(43):804.

[3]RUOFF P. Introducing temperature-compensation in any reaction kinetic oscillator model[J]. Journal of Interdisciplinary Cycle Research, 1992,(23):92.

[4]HONG C I, CONRAD E D， TYSON J J. A proposal for robust temperature compensation of circadian rhythms[J]. Proc Natl Acad Sci USA, 2007,(104)：1195.

[5]ZON J S, VAN, LUBENSKY D K， ALTENA P R H， PIETER R T W. An allosteric model of circadian KaiC phosphorylation[J]. Proc Natl Acad Sci USA, 2007,(104):7420.

[6]FRANCOSI P, DESPIERRE N， SIGGIA E D. Adaptive temperature compensation in circadian oscillations[J]. Plos Computational Biology, 2012,(8):495.

[7]ALON U. An introduction to systems biology: design principles of biological circuits[J]. Chapman & Hall/crc Boca Ration Fl， 2006，(5)：59.

[8]IMAN R L, DAVENPORT J M， ZEIGLER D K. Latin Hypercube Sampling Program User‘s Guide[J]. Albuquerque NM: Sandia Labs， 1980，(5)：25.

DOI：10.14182/J.cnki.1001-2443.2016.04.002

收稿日期：2016-05-26

基金项目：国家自然科学基金(11174013).

作者简介：王宏利(1969-)，男，安徽歙县人，安徽师范大学物理系1988级校友，北京大学物理学院教授，博士生导师.

中图分类号：O59

文献标志码：A

文章编号：1001-2443(2016)04-0315-05

Numerical Analysis of Oscillatory Regulatory Networks with Temperature-Independent Oscillation Period

WANG Hong-li,WU Li-li

(School of Physics, Beijing University, Beijing 100871， China)

Abstract:Oscillatory gene interaction networks whose oscillation period is independent of temperature were theoretically investigated with multiple-node-networks having up to twenty nodes and with few-node-networks with only three nodes. Analyses revealed that the temperature independent oscillation period can be achieved through proper re-linkages between the nodes. With only inhibitory interactions in the networks, and without fine-tuning parameter values, most of multiple-node networks can evolve into proper topologies and oscillate with a period not affected by temperature fluctuations. The analysis revealed that temperature-compensated oscillations occur at the system level and depend strongly on the topological structure of the networks.

Key words:robustness; oscillation; biological network

引用格式：王宏利，吴丽莉.振荡周期不受温度影响的生物调控网络的数值研究[J].安徽师范大学学报：自然科学版，2016，39(4)：315-319.