辐射噪声线谱多涡卷混沌同步化方法研究

刘树勇, 位秀雷, 方　煊, 王　基

(海军工程大学 动力工程学院，武汉　430033)



辐射噪声线谱多涡卷混沌同步化方法研究

刘树勇, 位秀雷, 方煊, 王基

(海军工程大学 动力工程学院，武汉430033)

摘要：针对非线性隔振系统不容易产生小幅值混沌振动的难题，选择合适的多涡卷混沌系统及其参数，实现了非线性隔振Duffing系统与涡卷混沌系统同步，重构了隔振系统响应信号的频谱，得到小幅值的宽频动力学行为。研究了不同参数条件下涡卷混沌行为以及对应的频谱特征，通过计算系统响应的最大Lyapunov指数，证实该系统处于混沌状态。通过参数驱动同步策略，发现非线性隔振系统在周期状态下，能够被有效地同步到混沌状态。而且从系统的分岔图以及吸引子相图可以看出，同步后系统的混沌响应具有明显的小幅值特性；同时驱动系统的涡卷参数可调，可以满足不同系统的同步需求。

关键词：多涡卷；混沌；同步；Duffing系统；小幅值

混沌是确定性系统产生的貌似随机的运动,混沌振动的一些优良特性可用于船舶动力机械的振动噪声控制[1]。一方面由于混沌能够改变其输出响应的频谱结构，从而改变潜艇辐射水声的频谱特征；另一方面，混沌使单频输入产生宽频输出，将集中于某一频率的能量分散到较宽的频带上，从而降低辐射噪声中的线谱成分[2-3]。

目前，基于混沌理论的线谱控制方法，在理论分析[4]、混沌区域预测[5]、隔振性能评估[6]以及混沌识别[7]等方面，取得了诸多成果。但实现其工程应用等方面还存在若干难点，其中，如何保持持续的小幅值混沌振动是线谱混沌化在工程实际应用的一个关键问题[8]。刘树勇等[9]提出一种机械式混沌同步系统，在主系统为大振幅混沌状态时，实现了子系统的小幅值混沌态。杨庆超等[10]设计了投影同步的试验台架，实现了隔振系统在变工况和小振幅条件下的混沌响应。上述方法大多集中在混沌的单涡卷和双涡卷形式，振动的能量还不能够充分地分散到其他频带上，阻碍了混沌化目标的实现。

近年来，多涡卷混沌吸引子的研究逐渐成为混沌研究领域的一个新方向[11]，相比于传统的单涡卷和双涡卷混沌系统，多涡卷混沌系统呈现出更为复杂的结构和动力学行为[12-13]。本文研究了不同参数条件下多涡卷混沌行为以及对应的频谱特征，采用多涡卷混沌同步方法将系统由周期运动状态诱导进入混沌状态，通过参数驱动同步策略，实现了非线性隔振Duffing系统的小幅值混沌行为。

1非线性隔振系统无量纲模型

单层非线性隔振系统模型如图1所示，得系统的运动微分方程如下：

(1)

式中：M为质量；C为阻尼器的黏滞阻尼系数；K1X+K3X3为非线性弹性恢复力；F0为作用在质块M上的激励力。其中，K3为负时，系统呈现软特性；K3为正时，系统呈现硬特性。

图1　Duffing隔振系统Fig.1 Duffing vibration isolation system

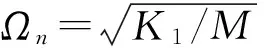
(2)

则有

(3)

将式(3)代入式(1)，得

(4)

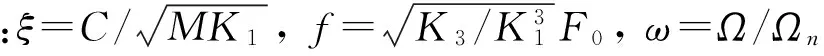
2混沌同步原理

考虑如下参数驱动单向耦合系统[8]：

(5)

式中：x={x1,x2,…,xn}为n维空间Rn中的驱动状态向量，y={y1,y2,…,ym}为m维空间Rm中的响应状态向量。F和G都为向量场，F：Rn→Rn，G：Rm→Rm。P表示系统之间的耦合状态向量，P：Rn→Rm，kt为表示耦合强度系数。

要判断式(5)是否存在广义同步，通常采用的方法是构造一个辅助系统y′)，它与式(5)第二式的形式一致：

(6)

式(5)第一式和第二式实现广义同步的充要条件是式(5)第二式和式(6)实现精确同步，由于式(5)第二式和式(6)实现精确同步与式(5)第二式渐近稳定等价，因此式(5)第一式与第二式实现广义同步当且仅当该系统第二式渐近稳定。

3非线性隔振系统的多涡卷混沌同步

辐射噪声线谱的混沌化，在本质上是要使得系统将振动能量从线谱转移到其他频率成分，从而削减特征频谱的能量。传统的混沌系统虽然具有宽频响应，但大多集中在单涡卷和双涡卷形式，振动的能量还不能够充分地分散到其他频带上，阻碍了混沌化目标的实现。构造多涡卷的混沌系统并与非线性隔振系统混沌同步，将为解决该问题提供新的思路。

选取具有鞍焦点的系统：

(7)

对应的Jacobi矩阵为：

将式(5)具体化为：

(8)

根据系统的Jacobi矩阵，当参数为u=-8,v=0.4,w=-6时，系统的特征值为λ1，2=0.2±2.821i,λ3=-6，这表明系统的行为将限制在某一区域，并具有类似蝴蝶吸引子的缠绕轨道。为了重构多涡卷混沌系统，取非线性函数为：

sgn[s-(2j-1)]}

(9)

联合式(8)和式(9)，可进一步得到具有非线性项的动力学系统：

(10)

当系统的参数在特定范围时，系统将呈现混沌行为。将式(10)作为驱动系统，式(4)作为被驱动系统，在式(4)中引入刚度系数后写成状态方程形式：

(11)

同步过程中采用参数驱动模式，将驱动信号p2作用于式(11)的线性刚度k1，因此得到系统的k1=kp2，其中，k为驱动强度，因此，得到：

(12)

4仿真研究

4.1驱动系统的动力学特性

对式(10)而言，取u=-8，v=0.4，w=-6，Q=1时，系统的响应如图2所示，此时系统的吸引子是由三个螺旋上升的涡卷构成，频率谱呈现连续谱状态，最大Lyapunov指数为0. 221。当Q的值进行调整时，系统涡卷数不断改变，Q为2时，生成5个涡卷，Q=3时生成7个涡卷(见图3,图4)。由此可见，调整该值能够得到不同的工作状态，为隔振系统的混沌同步奠定了良好的基础。

图2　u=-8;v=0.4;w=-6，Q=1时，系统的响应Fig.2 System response when u=-8;v=0.4;w=-6，Q=1

图3　u=-8;v=0.4;w=-6，Q=2时，系统的响应Fig.3 System response when u=-8;v=0.4;w=-6，Q=2

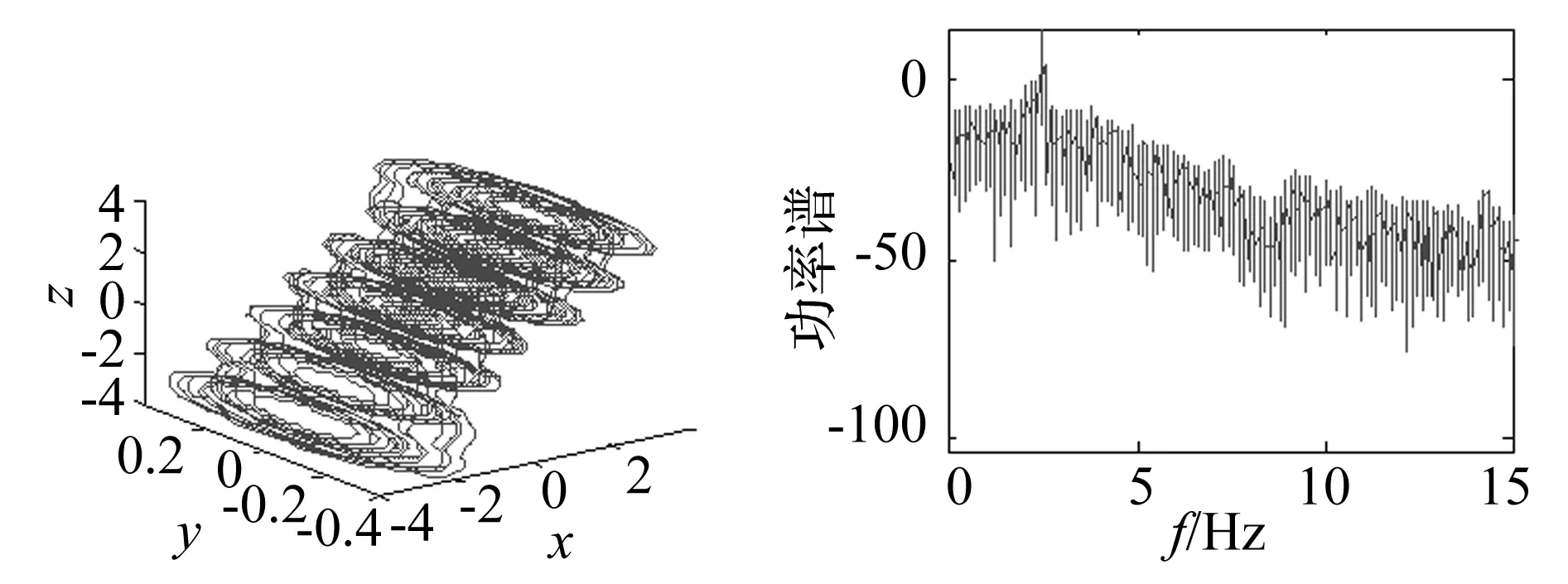
图4　u=-8;v=0.4;w=-6，Q=3时，系统的响应Fig.4 System response when u=-8;v=0.4;w=-6，Q=3

4.2被驱动系统的动力学特性及同步响应

(1) 动力学特性分析

以线性刚度为负的硬弹簧Duffing系统为研究对象，对式(11)取不同的参数进行分析。首先采用全局分岔方法来分析系统的整体动力学性态。当系统的参数为k1=-1，k3=1，ξ=0.3，ω=1.2，以激励力幅值f为变化参数，得到系统的分岔图如图5所示。从图中可以得知系统在初始阶段出现周期1的解，随后出现多周期解，经过倒分岔进入周期1解，再次经过倍周期分岔后，进入混沌状态。但是激励力的幅值和系统响应的幅值已经明显增大，更确切地说，这种大幅值混沌振动状态和隔振系统小幅值混沌状态要求相矛盾，必须采取新的方式诱导系统进入有益的混沌行为中。

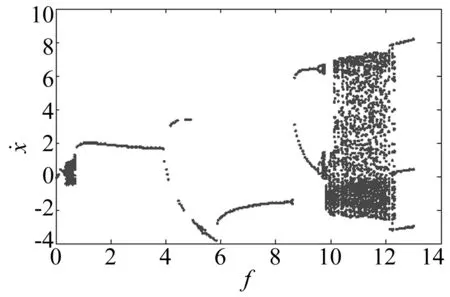
图5　系统的分岔图Fig.5 Bifurcation diagram of the system

根据全局分岔图，当系统的其他参数不变，激励力幅值大小f=11.5时，系统的胞映射图如图6所示，从中可以看出，系统的对初值具有很强的敏感性，混沌吸引域相互缠绕，具有明显的分形结构。系统相平面的吸引子如图7所示，功率谱图如图8所示。吸引子不同于不动点、极限环和环面等平庸吸引子，而是具有自相似结构的奇怪吸引子，功率谱呈现谱特征。系统的行为具有混沌特性，但混沌响应处于较大振幅状态。

从系统的分岔规律可知，当参数选择为f=2.3时，系统出现周期1解，通过PMUCR胞映射法得到系统的胞映射图如图9所示，在该图中可以看出，当系统的初始条件取不同的值时，都将呈现周期1响应。图10是系统在该范德玻尔平面上的解，所有的曲线都收敛在一个吸引子上，这验证了系统的行为具有唯一性。

图6　系统的胞映射图Fig.6 Cellular mapping of the system

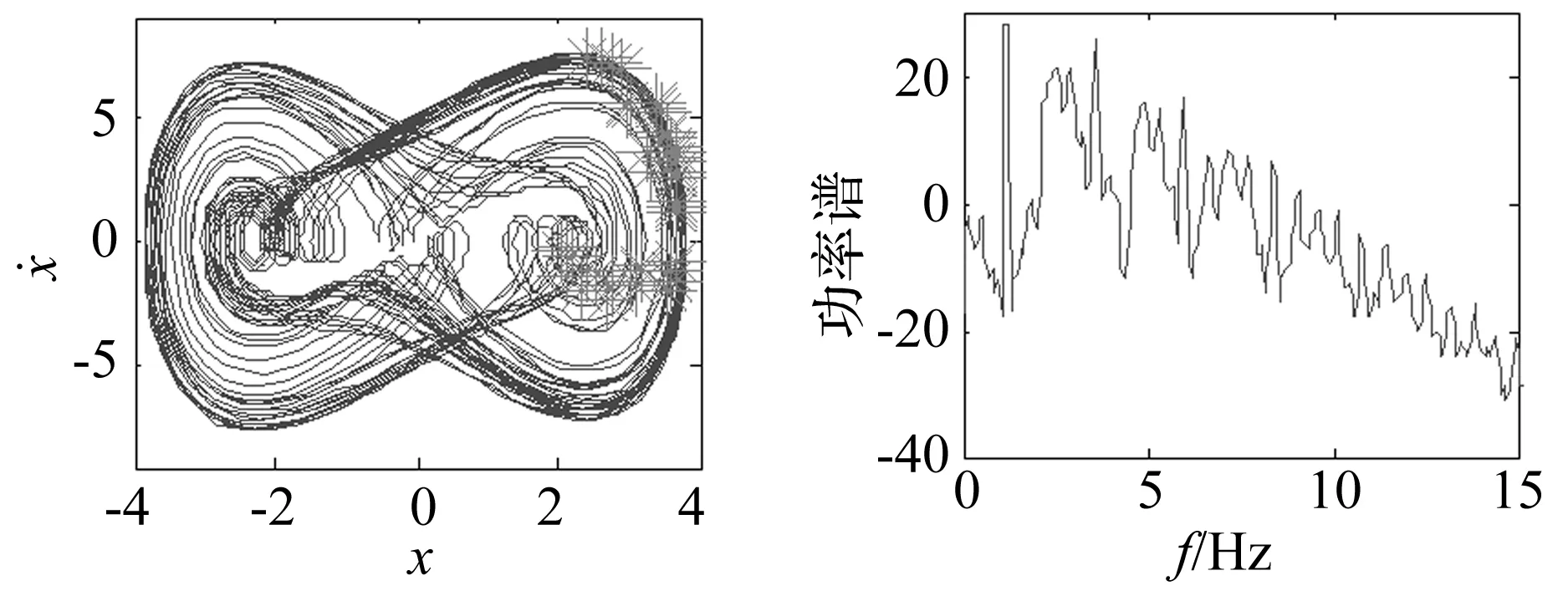
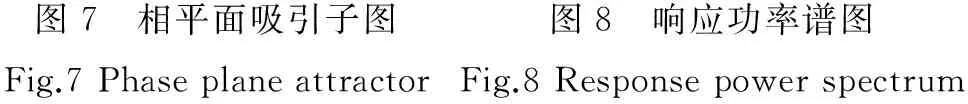
图7 相平面吸引子图Fig.7Phaseplaneattractor图8 响应功率谱图Fig.8Responsepowerspectrum

图9 周期1解的胞映射图Fig.9Cellmappingofperiodic1solutions图10 在范德玻尔平面上的解Fig.10SolutionintheplaneofvanderBohr

对系统求解，到了系统的相平面图和Poincare截面图(见图11)。系统的相图是一个椭圆，Poincare截面图只有一个点，因此当没有使用驱动系统时，此时系统不会因为初始条件的不同而产生混沌运动，其响应的位移功率谱如图12所示。

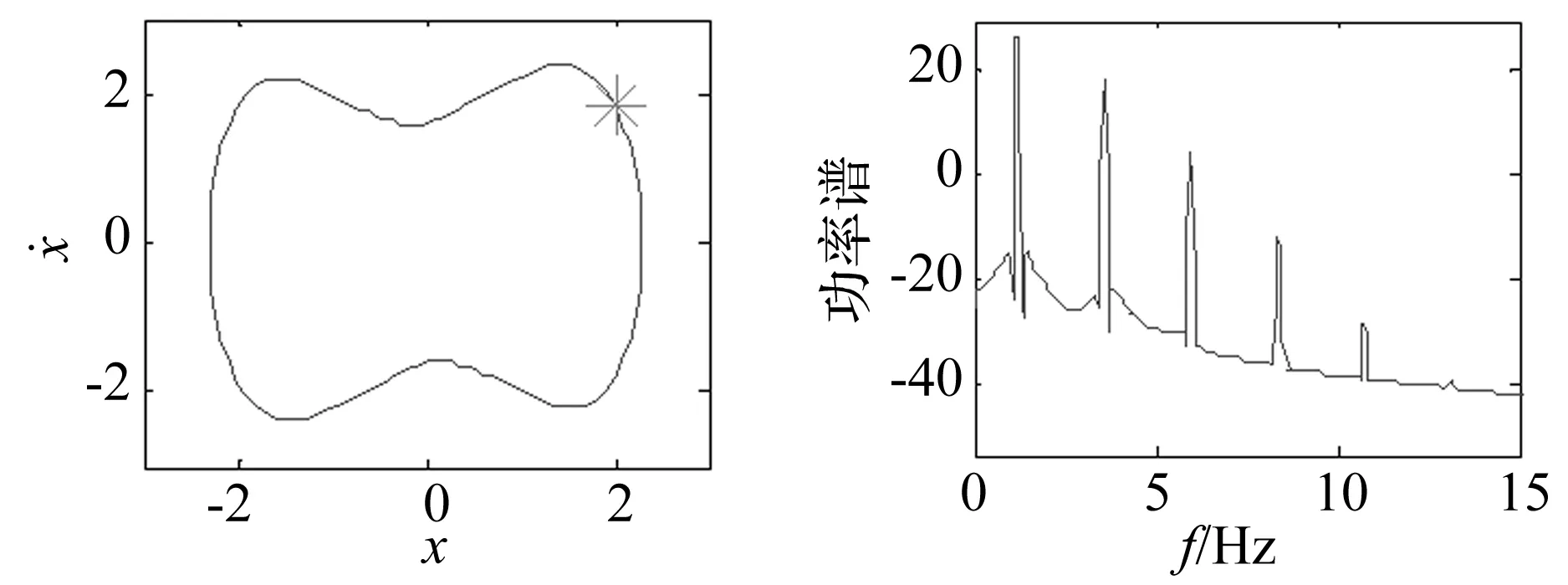
图11 系统响应的相平面图Fig.11Phaseplanofsystemresponse图12 系统响应的功率谱图Fig.12Powerspectrumofsystemresponse

(2) 混沌同步结果

当系统的参数为f=2.3，k1=-1，k3=1，ξ=0.3，ω=1.2时，系统处于周期1状态。采用3涡卷同步时，驱动强度k=1，能够将该周期1状态驱动进入混沌状态，而最大幅值只有2.54，如图13所示，响应的最大Lyapunov指数为0.118，显然是一种获得小幅值混沌的有效手段。而不采用同步方式时，系统的参数为k1=-1，k3=1，ξ=0.3，ω=1.2，但激励的幅值需要达到f=11.5该系统才能够出现混沌，而响应的幅值达到7.78，两者的比较如图14所示。

图13 同步混沌响应相图Fig.13Phasediagramofchaoticsynchronizedresponse图14 非同步混沌响应相图Fig.14Phasediagramofchaoticnon-synchronizedresponse

5结论

通过对非线性隔振Duffing系统的全局分岔分析，得到了系统随激励力幅值变化的整体性态图，观察到了系统在在不同参数时的周期1、周期2解以及由倍周期分岔导致的混沌行为。应用PMUCR胞映射方法得到了系统在不同参数区域时初始条件对系统解的影响，在混沌参数范围时，胞映射图具有明显的分形结构，反映了混沌系统内部复杂但有规律的动力学特征。在周期1解情况下，初始条件对系统的影响不明显，应用范德玻尔平面证实了解的唯一性。由于系统本身产生混沌时，处于大幅度振动状态，不利于辐射噪声的控制，因此采用多涡卷混沌同步方法将系统由周期运动状态诱导进入混沌状态，实现了非线性隔振Duffing系统的小幅值混沌行为，从而为噪声线谱混沌控制提供有益参考。

参 考 文 献

[1] 刘树勇，朱石坚，俞翔. 准周期激励非线性隔振系统的混沌研究[J]. 船舶力学，2010，14(1)：141-147.

LIU Shu-yong,ZHU Shi-jian,YU Xiang. Study on the chaos of nonlinear vibration isolation system under quasi-periodic excitation[J]. Journal of Ship Mechanics,2010,14(1):141-147.

[2] Lou J J，Zhu S J，He L，et al. Application of chaos method to line spectra reduction[J].Journal of Sound and Vibration, 2005，286(3):645-652.

[3] Zhu S J，Zheng Y F，Fu Y M. Analysis of non-linear dynamics of a two-degree-of-freedom vibration system with non-linear damping and non-linear spring[J].Journal of Sound and Vibration,2004，271(1/2):15-24.

[4] Yu X，Zhu S J，Liu S Y．Bifurcation and chaos in multi-degree-of-freedom nonlinear vibration isolation system[J]. Chaos，Solitons，and Fractals, 2008，38 ( 5 ): 1498-1504.

[5] 张振海，朱石坚，楼京俊. 基于跟踪混沌化方法的线谱控制技术研究[J]. 振动与冲击，2011，30(7):40-44.

ZHANG Zhen-hai,ZHU Shi-jian,LOU Jing-jun. Line spectra reduction of a vibration isolation system based on tracking chaotification method[J]. Journal of Vibration and Shock, 2011，30(7):40-44.

[6] 浣石，陶为俊，朱石坚，等. 硬特性非线性隔振装置混沌动力学特性研究[J]. 振动与冲击，2011，30(11):245-248.

HUAN Shi, TAO Wei-jun, ZHU Shi-jian, et al. Chaotic dynamics of hardening nonlinear isolation device[J]. Journal of Vibration and Shock, 2011，30(11):245-248.

[7] 刘树勇，杨庆超，位秀雷，等. 邻近点快速搜索算法在混沌识别中的应用[J]. 华中科技大学学报:自然科学版，2012，40(11):89-92.

LIU Shu-yong, YANG Qing-chao, WEI Xiu-lei, et al.The application of fast searching nearest points method to chaos identification [J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2012，40(11):89-92.

[8] Wen G L，Lu Y Z，Zhang Z Y，et al．Line spectra reduction and vibration isolation via modified projective synchronization for acoustic stealth of submarines[J]. Journal of Sound and Vibration， 2009，324: 954-961.

[9] 刘树勇，杨爱波，杨庆超，等. 机械式混沌同步系统动力学特性研究[J]. 华中科技大学学报:自然科学版，2012，40(8):108-111.

LIU Shu-yong, YANG Ai-bo, YANG Qing-chao,et al. Dynamic characteristics of mechanical chaos synchronization systems [J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2012，40(8):108-111.

[10] 杨庆超，朱石坚，刘树勇，等. 投影混沌同步试验研究[J]. 振动与冲击，2012，31(20):126-130.

YANG Qing-chao,ZHU Shi-jian,LIU Shu-yong, et al. Experimental study on projective synchronization to a vibration isolation system[J]. Journal of Vibration and Shock,2012，31(20):126-130.

[11] 谌龙，彭海军，王德石. 一类多涡卷混沌系统构造方法研究[J]. 物理学报，2008，57(6):3337-3341.

CHEN Long, PENG Hai-Jun, WANG De-Shi. Study on the construction of a family of multi-scroll chaotic systems[J]. Acta Physica Sinica, 2008，57(6):3337-3341.

[12] Zhang C X，Yu S M. Generation of grid multi-scroll chaotic attractors via switching piecewise linear controller[J]. Physics Letters A，2010，374(30):3029-3037.

[13] 张朝霞，禹思敏. 用时滞和阶跃序列组合生成网格多涡卷蔡式混沌吸引子[J]. 物理学报，2009，58(1):120-130.

ZHANG Chao-xia, YU Si-min. Generation of grid multi-scroll Chua’s chaotic attractors with combination of hysteresis and step series[J]. Acta Physica Sinica, 2009，58(1):120-130.

基金项目：国家自然科学基金(51179197);国家自然科学基金面上项目(51579242);海洋工程国家重点实验室(上海交通大学)开放课题(1009);国家留学基金委资助

收稿日期：2015-02-11修改稿收到日期：2015-08-10

通信作者位秀雷 男，博士生，1988年10月生

中图分类号:O322

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.14.022

Multi-scroll chaotic synchronization method for radiated noise line spectrum

LIU Shu-yong, WEI Xiu-lei, FANG Xuan, WANG Ji

(College of Power Engineering, Naval University of Engineering, Wuhan 430033, China)

Abstract:The nonlinear vibration isolation system is hard to produce chaotic vibration with small amplitude. In order to solve the problem, an appropriate multi-scroll chaotic system and its parameters were selected and the synchronization between the multi-scroll chaotic system and Duffing system were achieved. The frequency and spectrum of the isolation system was reconstructed, and then the dynamics behavior with broadband spectrum and small amplitude was realized. The chaotic dynamic characteristics under different parameters of the multi-scroll system and the corresponding frequency spectrum characteristics were studied. The largest Lyapunov exponent of the system response was calculated to confirm the chaotic state of system. By using the parametric driven synchronization strategy, it is found that the synchronization between the periodic state and chaotic state of the nonlinear isolation system can be achieved exactly, and the chaotic response after synchronization has obvious characteristics of small amplitude which can be presented in the bifurcation and attractor diagram. In addition, the scroll number of drive system is adjustable, so the synchronizations of different systems can be implemented.

Key words:multi-scroll; chaos; synchronization; Duffing system; small amplitude

第一作者 刘树勇 男，副教授，1975年11月生