库前水位对混凝土重力坝抗爆安全性能的影响

李　麒, 王高辉， 卢文波， 陈　明

(武汉大学 水资源与水电工程科学国家重点实验室，武汉　430072)



库前水位对混凝土重力坝抗爆安全性能的影响

李麒, 王高辉， 卢文波， 陈明

(武汉大学 水资源与水电工程科学国家重点实验室，武汉430072)

摘要：现代战争有征兆可察，通过预警放水不仅可以有效提高大坝的抗爆安全性能，同时能够减少大坝失事风险损失。基于显示动力分析平台，考虑爆炸高加载率下的混凝土应变率效应，建立水下爆炸条件下炸药-气体-库水-坝基-坝体全耦合动力分析模型，对比分析了正常蓄水位及死水位条件下混凝土重力坝水下爆炸毁伤破坏特征及抗爆安全性能；同时针对战时预警放水条件，分析不同库前水位下混凝土重力坝的动态响应特征、破坏发展过程及毁伤空间分布特征，全方位研究了库前水位对大坝抗爆安全性能的影响。结果表明：对于混凝土重力坝，随着库前水位的降低，坝体损伤破坏范围逐渐减小；当库前水位降低到大坝下游折坡以下时，大坝抗爆安全性能得到显著的提高。

关键词：混凝土重力坝；库前水位；抗爆安全性能；全耦合模型；水下爆炸；损伤演化

近年来，恐怖袭击活动在世界范围内频发，具有明显政治经济效益的高坝成为恐怖分子的重点打击目标。且随着精确制导技术的发展，高坝受到的威胁大大增加。我国处在高坝快速发展时期，一大批100～300 m级的高坝已建成或正在建设中，如龙羊峡水电站(178 m)、二滩水电站(240 m)、澜沧江的黄登水电站(202 m )、白鹤滩水电站(284 m)等，这些大坝水位高、库容大，一旦失事将对下游造成巨大的人员伤亡和财产损失。由于爆炸冲击波在水中传播时所产生的破坏作用比在空气中强烈得多[1]，水下爆炸对于混凝土重力坝破坏潜能最大。通过战时预警放水，不仅可以提高大坝抗爆性能，同时也可以减小战时大坝的失事风险损失，如三峡工程枢纽建筑物设计中，已考虑战时与平时运用相结合，大坝有大泄量的底孔，降低水库水位所需时间较短，由正常蓄水位175 m降至135 m最多只需7天，可以有效减少溃坝损失。因此，研究库前水位对大坝抗爆安全性能的影响具有重大战略意义。

目前，关于大坝在水下爆炸冲击荷载作用下的动态响应及失效模式的研究主要是在正常运行水位条件下进行。如张启灵等[2]采用声学介质描述库水，考虑键槽作用的两种极端情况及混凝土的受拉、受压损伤，探讨了高水位运行下近水面水下爆炸对高拱坝结构安全性能的影响；Yu[3]以非线性显示动力分析程序LS-DYNA为平台建立水下爆炸全耦合模型，采用ALE算法对水下接触爆炸下的大坝动力响应进行了研究，得到大坝的损伤破坏分布；Linsbauer[4]通过建立库水-坝体耦合模型，对库底爆炸冲击荷载作用下混凝土重力坝(上游面含裂缝)的动力响应、稳定性进行了研究；张社荣等[5-6]通过构建水下爆炸混凝土重力坝全耦合模型，分别从大坝高度、起爆深度、爆心距、炸药量等方面，探讨了正常蓄水位条件下混凝土重力坝的水下爆炸失效模式；Lu等[7]针对高坝灾难控制问题,选用软质聚氨酯材料作为保护材料,对混凝土高坝在水下爆炸冲击波作用下的防护进行了研究。然而,目前从降低库前水位研究混凝土重力坝水下抗爆安全性能的成果甚少，这也是本文所做的主要工作。

本文从库前水位这一人为可控因素出发，基于显示非线性动力分析平台，考虑爆炸高加载率下的混凝土应变率效应，建立水下爆炸条件下炸药-气体-库水-坝基-坝体全耦合动力分析模型，分析不同库前水位下大坝在水下爆炸冲击荷载作用的动态响应特征、破坏发展过程及毁伤空间分布特征，全方位研究了库前水位对大坝抗爆安全性能的影响，为已建成坝体的战时应对提供理论基础。

1材料本构模型

1.1爆炸高加载率下的混凝土非线性动态损伤本构模型

爆炸高加载率荷载作用下，混凝土材料通常会表现出压缩效应、应变率效应等特性[8]。Riedel等[9]在HJC模型[10-11]的基础上，考虑应变硬化及偏应力张量第三不变量提出RHT模型，能综合反映混凝土材料的拉压损伤、应变率效应、软化及失效等现象。RHT模型中引入了弹性极限面、失效面、及残余强度面分别用于描述混凝土的初始屈服强度、失效强度及残余强度的变化情况，如图1所示。

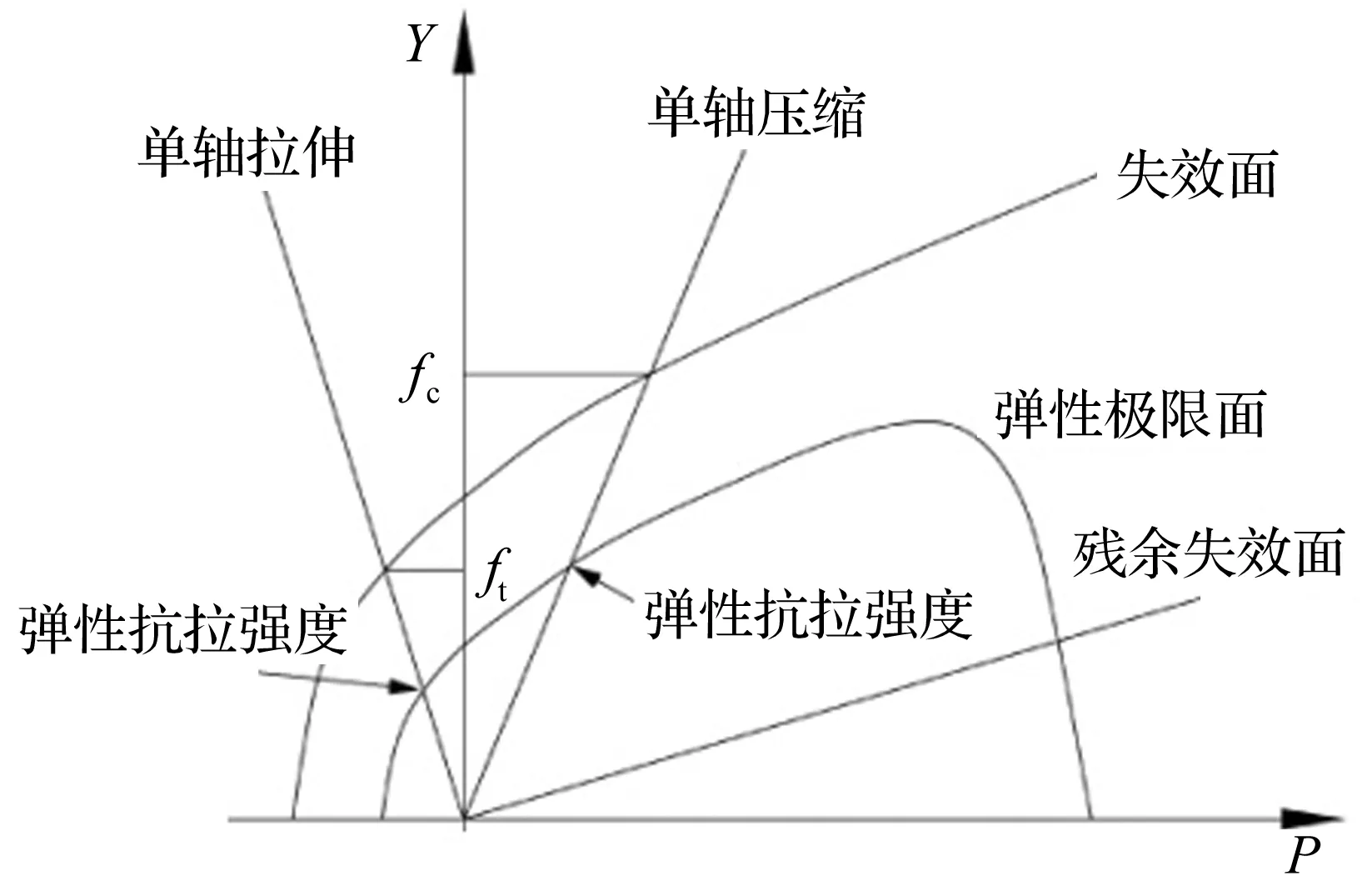
图1　RHT本构模型的三个失效面Fig.1 Three failure surface of RHT constitutive model

RHT失效面方程为：

(1)

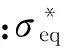
(2)

式中：fc为准静态单轴抗压强度，取3.5×107Pa。

(3)

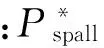
(4)

式中：α为压缩应变率指数，δ为拉伸应变率指数，可通过实验测得。

R3(θ)=

(5)

式中：Q2=Q0+BQp*,0.51≤Q2≤1.0,Q0为拉压子午比，BQ为脆性韧性转变参数，均可由实验测得。

RHT弹性极限面方程为：

(6)

式中：函数FCAP(P)为盖帽函数，用于限制静水压力下的弹性偏应力。

RHT残余强度面方程为：

(7)

式中:B为残余失效面常数，M为残余失效面指数，分别取0.7，0.8[12]。

当前屈服面介于弹性极限面与最大失效面之间时：

Ypre=Yela+εpl,eq(Yfail-Yela)/εplhard,eq

(8)

式中：εpl,eq和εplhard,eq分别为当前失效面和最大失效面对应的塑性应变。

RHT本构模型的损伤定义为：

(9)

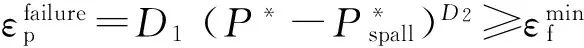
1.2坝基岩体非线性动力本构模型

根据已有研究成果，在进行坝基岩体数值计算时，对其分别采用Linear状态方程，Johnson-Cook强度模型[10]和Principal Stress失效模型。

Linear状态方程形式简单且适用性强，其表达式如下：

p=k(ρ/ρ0-1)

(10)

式中：p为压力，k为体积模量，ρ为材料即时密度，ρ0为材料初始密度。

Johnson-Cook强度模型可用于描述大变形、大应变率问题，适用于爆炸问题的描述，其表达式如下：

(11)

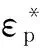
(12)

式中：T为当前温度，Tmelt为材料熔化温度，Troom为室温。

Principal Stress失效模型主要用于控制岩石的主拉应力，由于在爆炸冲击荷载作用下，岩石的动抗拉强度远远小于其动抗压强度，当拉应力超过其动抗拉强度时岩石即破坏，同时考虑到岩石屈服应力较动抗拉强度大，因此数值计算时采用主拉应力来控制其破坏。

根据我国坝基岩石分类情况，花岗岩是比较典型的一类岩石且分布较为广泛，故在对坝基岩体进行数值模拟时以花岗岩为研究对象，其各项参数为：密度ρ=2 630 kg/m3,弹性模量E=50 GPa，泊松比ν=0.16，屈服强度σs=40 MPa，切线模量Et=40 MPa，抗拉强度ft=24 MPa，抗压强度fc=70 MPa。

2状态方程

2.1爆轰产物状态方程

炸药采用AUTODYN材料库中提供的TNT炸药材料模型，并用JWL[13]状态方程描述：

p=A1(1-ω/R1V)e-R1V+

B1(1-ω/R2V)e-R2V+ωE0/V

(13)

式中：p为爆轰压力，V=1.00为爆轰产物的相对体积，E0=6.0 GPa为初始比内能，特征参数A1=373.77 GPa、B1=3.75 GPa、R1=4.15、R2=0.90、ω=0.35为材料常数。

2.2水状态方程

数值计算时，对于水体采用Polynomial状态方程[13]，其在不同压缩状态下具有不同的形式。当水压缩时(μ>0)，状态方程为：

P=A1μ+A2μ2+A3μ3+(B0+B1μ)ρ0e

(14)

当水膨胀时(μ<0)，状态方程为：

P=T1μ+T2μ2+B0ρ0e

(15)

当水既不压缩也不膨胀时，可简化为：

P=B0ρ0e

(16)

式中：P为水中压力；μ为压缩比，μ=ρ/ρ0-1；e为水的内能；ρ0为水密度，取为1 g/cm3；A1=T1=2.2×106kPa，A2=9.54×106kPa，A3=1.46×106kPa，B0=B1=0.28，T2=0。

2.3空气状态方程

数值计算时，对于空气采用Ideal Gas状态方程：

p=(γ-1)ρe

(17)

式中：ρ为空气密度，取1.225 kg/m3；e为空气初始内能，取2.068×105kJ/kg；γ为材料常数，取1.4。

3水下爆炸全耦合模型的建立与验证

3.1水下爆炸全耦合模型的建立

选取国内某混凝土重力坝作为研究对象，进行不同库前水位时水下爆炸冲击荷载作用下混凝土重力坝的损伤演化过程及抗爆安全性能研究。水库正常蓄水位1 791.0 m，死水位1 746.0 m，挡水坝段最大坝高120 m，单坝段宽度取15 m，大坝计算模型示意图如图2所示。

图2　大坝计算模型示意图(m)Fig.2 Calculation region of non-flow dam(m)

考虑炸药起爆、冲击波传播、起爆气体与库水以及库水与大坝和坝基之间的动态耦合作用，建立水下爆炸条件下炸药-气体-库水-坝基-坝体全耦合动力分析模型，如图3所示。有限元计算模型主要包含库水、大坝、空气、基岩以及TNT炸药五种物质的耦合。其中库水、空气及TNT炸药采用Euler网格建模，大坝及基岩采用Lagrange网格建模，库水与坝体和坝基之间采用流固耦合算法。由于几何模型的对称性，在进行模型建立时，只取对称面一侧为研究对象以减少计算量。考虑到水下爆炸荷载为瞬时冲击荷载，作用时间较短，表现为坝体的局部破坏，因此坝基仅选取局部范围进行计算，用于考虑坝体与坝基之间的相互作用，同时减少计算量。图3给出的是正常蓄水位条件下的水下爆炸全耦合计算模型，其他水位条件下的水下爆炸全耦合计算模型采用类似方法建立，在此不予给出。TNT装药量取Q=306 kg(GBU-28制导炸弹装药量)，炸药中心单元尺寸为100 mm，并随爆心距的增大而逐步增大，坝头部分单元尺寸为100 mm，并朝着坝底方向尺寸逐步增大，整个模型含2 107 440个单元，2 240 998个节点。为分析各计算模型大坝动态响应，在坝顶设置相应的监测点。

图3　水下爆炸全耦合计算模型Fig.3 Fully-coupled calculation model subjected to underwater explosion

受计算时间和能力的限制，全耦合模型中的库水、空气和坝基仅截取了有限区域。为了使冲击波在截断边界上无反射，在截断面边界上施加无反射透射边界条件(Transmission Boundary)，以此来模拟库水、空气、坝基的半无限区域。同时在对称面上施加对称约束，坝基底部施加全约束。

3.2模型验证

为了验证3.1节全耦合动力分析模型的合理性和正确性，建立了自由场水下爆炸模型，对自由场水下爆炸冲击波传播过程进行模拟，并将数值模拟的计算值与Zamyshlyayev经验公式[14]的经验值进行对比。

本文利用x、y、z三轴的轴向对称性只建立了1/8的计算模型，如图4所示。模型计算区域为10 m×10 m×10 m，网格尺寸100 mm，立方体TNT装药量为306 kg，起爆点位于炸药中心，截断边界采用无反射边界，以此来模拟库水半无限区域。

图4　水自由场爆炸计算模型Fig.4 Computational model of water free-field explosion

图5给出了自由场水下爆炸冲击波传播的峰值压力对比。在近爆区域，由于试验测量误差较大，数值模拟得到的爆炸冲击波峰值压力和冲量与经验公式得到的峰值压力存在一定差异。当爆心距增大(d>3 m)后，峰值压力的经验值和数值模拟值差距逐渐较小，拟合程度也越来越高。综上所述，3.1节所建全耦合动力分析模型可靠性较强，可用作后续计算及分析。

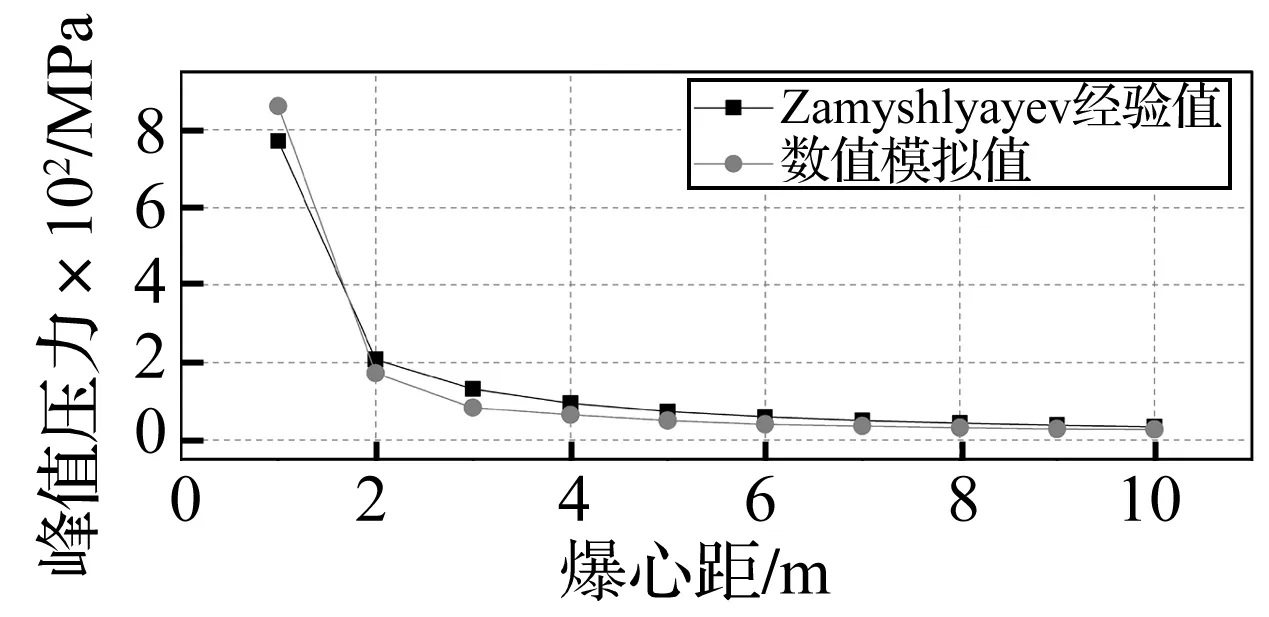
图5　自由场水下爆炸冲击波传播峰值压力对比Fig.5 Comparison of peak pressure of shock wave in free-field underwater explosion

4正常蓄水位及死水位条件下的大坝抗爆安全性能研究

4.1正常蓄水位条件下

为了研究库前水位对大坝抗爆性能的影响，首先建立正常蓄水位条件下水下爆炸全耦合模型。图6(a)给出了该研究工况下的大坝计算示意图，炸药起爆深度和爆心距均取10 m，TNT炸药量为306 kg。通过数值模拟计算得到坝体损伤演化过程，如下图6(b)～(h)所示。图例中的损伤值0～1表示混凝土单元从未发生损伤破坏状态到完全破坏状态，当损伤值大于0.75时，表示坝体混凝土产生了宏观裂缝[15]。

当炸药在水中起爆后，水下爆炸冲击波将经库水传播到坝体，当t=8 ms时，水下爆炸产生的高压冲击波经库水传至大坝上游表面处，坝体表面在冲击波荷载的直接作用下发生一定的压缩损伤破坏，同时在自由水面与坝体交界处由于水面切断效应[16]产生一定的损伤破坏，如图6(b)所示；随后冲击波向混凝土重力坝内部传播，并衰减为一种压缩应力波，由于混凝土材料抗压强度较大，混凝土内部受压损伤较小；当t=12 ms时，压缩应力波传播至坝体下游面时，由于空气波阻抗远小于混凝土波阻抗，在大坝下游自由面处将反射形成强烈的拉伸应力波，而混凝土材料的抗拉强度较抗压强度小很多，同时考虑到应力集中效应，下游折坡将在此区域产生拉伸损伤破坏，如图6(c)所示；随着拉伸应力波向坝体内部传播，下游折坡处的拉伸损伤不断向上游扩展，当t=20 ms时，扩展深度达7.3 m，当t=40 ms时，扩展深度达13.5 m，同时随着应力波在大坝内部反复折射作用，形成了不规则损伤破坏，如图6(d)～(f)所示；当t=50 ms时，损伤破坏继续向上游侧发展，并最终贯穿坝体，同时，受冲击波荷载的作用，坝体产生一定的整体动力响应，导致坝踵处也发生较小范围的拉伸损伤破坏，如图6(g)～ (h)所示。

图6　正常蓄水位下坝体损伤演化过程Fig.6 Damage evolution process of the dam under normal water level condition

4.2死水位条件下

为了研究当库前水位降低到死水位时大坝的抗爆安全性能，建立死水位条件下水下爆炸全耦合模型，图7(a)给出了该研究工况下的大坝计算示意图，炸药起爆深度和爆心距均取10 m。通过数值模拟计算得到坝体损伤演化过程，如下图7(b)～(d)所示。

图7　死水位下坝体损伤演化过程Fig.7 Damage evolution process of the dam under dead water level condition

由图7可知，水下爆炸冲击荷载作用下，混凝土重力坝损伤破坏区域主要集中于大坝下游折坡处、正对炸药中心的大坝上游表面、自由水面与坝体交界处以及大坝坝踵处。当t=20 ms时，大坝上游表面正对炸药中心处及自由水面与坝体交界处产生一定损伤破坏，但下游折坡处并未发生明显的损伤破坏，如图7(b)所示；当t=40 ms时，大坝下游折坡处在拉伸应力波的作用下产生一定的拉伸损伤破坏，破坏深度约为1.8 m，同时，由于坝体的整体动力响应，在坝踵处发生较小范围的拉伸损伤破坏，如图7(c)所示；当t=60 ms时，随着拉伸应力波向坝体内部传播，下游折坡处的拉伸损伤破坏不断向上游扩展，扩展深度达3.6 m，如图7(d)所示。由图7与图6中正常蓄水位下坝体损伤演化过程对比分析可知，死水位下大坝下游折坡处的局部损伤破坏明显较小，主要原因在于，当水下爆炸冲击波传至自由水面时，由于水面的切断效应，能量的传播受到阻碍，自由水面以上的坝体部位受到损伤也会相应减小；同时，大坝下游折坡处损伤破坏开始出现的历时较长，而坝踵处会较早出现拉伸破坏。

4.3对比工况条件下

考虑到上述两水位下炸药的起爆位置不同，为排除炸药起爆位置对坝体损伤程度的影响，另研究一对比工况，该工况下，库前水位位于正常蓄水位，爆心距取10 m，起爆位置与死水位时的起爆位置相同，即起爆深度为55 m，大坝计算示意图如图8(a)所示，坝体损伤演化过程如图8(b)～ (d)所示。

图8　对比工况下坝体损伤演化过程Fig.8 Damage evolution process of the dam under contrast condition

由图8可知，对比工况条件下，混凝土重力坝在水下爆炸冲击荷载作用下发生严重的损伤破坏，当t=60 ms时，坝体下游折坡处产生贯穿性损伤破坏，坝踵也产生一定的拉伸损伤破坏，如图8(d)所示。对比图6和图8可知，当库前水位位于正常蓄水位下，起爆深度分别为10 m、55 m时坝体的局部损伤破坏均较严重，都在大坝下游折坡处形成了贯穿性损伤破坏；对比图7和图8可知，当炸药起爆位置相同，库前水位位于正常蓄水位时坝体损伤破坏程度较死水位时坝体损伤破坏程度严重得多，由此说明当爆心距和起爆深度相同时，4.2节的相关结论与炸药的起爆位置关系不大。

进一步可由其坝顶上游面x方向速度-时间曲线加以说明，如下图9所示，正常蓄水位下坝顶上游面速度峰值达到了1.01 m/s，对比工况下速度峰值约为0.79 m/s，两种情况下坝体响应均较为剧烈，而死水位下速度峰值仅为0.41 m/s，坝体响应很小。

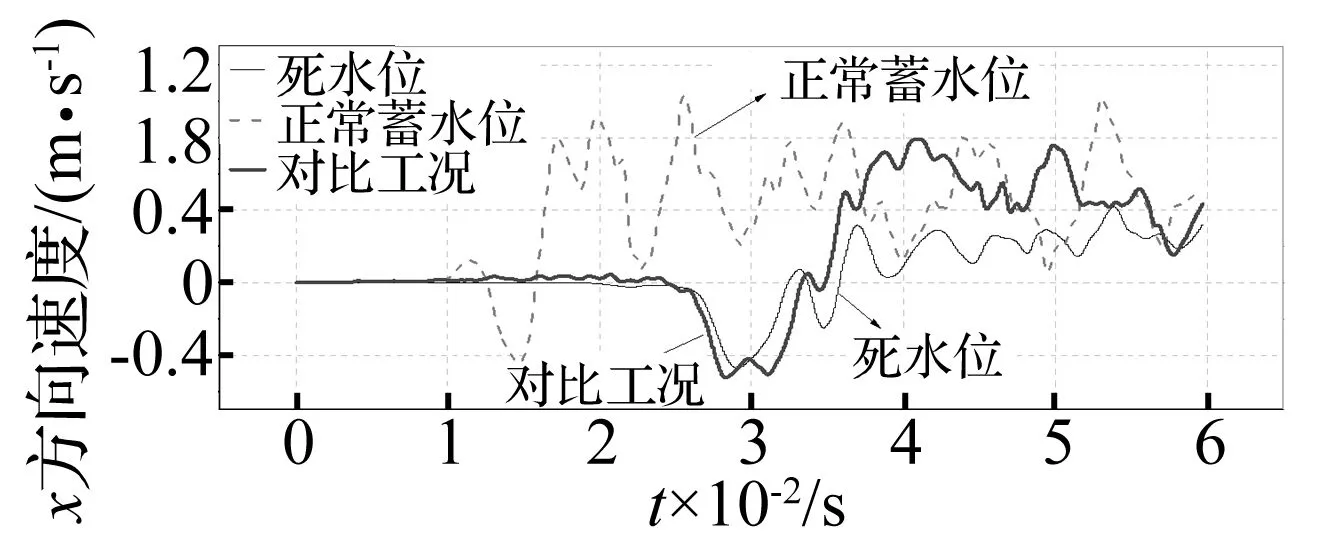
图9　坝顶上游面x方向速度曲线Fig.9 x-velocity of the upstream face of the dam crest

由此可知，对于混凝土重力坝，随着库前水位的降低，坝体损伤破坏范围逐渐减小；当库前水位降低到死水位时，大坝损伤破坏范围与正常蓄水位相比显著减小，这主要是由库前水位的降低所造成的。

5其他水位处大坝抗爆安全性能研究

通过对大坝在正常蓄水位及死水位的破坏过程分析，得到死水位下大坝局部损伤范围很小、大坝抗爆安全性能较高这一结论，但由于战时时间紧迫，库区水位降低到死水位一般需数天到十几天，是否必须降低到死水位才能保证大坝安全需进一步分析。

考虑到4.1～4.3节中，水下爆炸冲击荷载作用下，混凝土重力坝损伤区域主要集中在大坝下游折坡处，由此选取大坝下游折坡作为研究对象，分别建立库前水位位于大坝折坡处、折坡以下10 m处及折坡以下20 m处水下爆炸全耦合模型，爆心距和起爆深度均为10 m，大坝的计算示意图及损伤演化过程分别如图10～12所示。

由图10可知，当库前水位位于折坡高程处时，在水下爆炸冲击荷载作用下，坝体下游折坡处产生较为严重的损伤破坏，破坏深度达到10 m，与图6正常蓄水位条件下坝体损伤破坏程度相差不大，据此可知，当库前水位位于大坝折坡高程以上时，通过降低库前水位并不能显著提高大坝抗爆安全性能；由图11可知，当库前水位位于大坝折坡以下10 m处时，坝体下游折坡处损伤破坏程度与正常蓄水位条件下相比减小幅度较大，大坝抗爆安全性能得到显著提高，当继续降低库前水位到折坡以下20 m时，如图12所示，下游折坡处损伤破坏程度与图11相比变化不大，据此可知，当库前水位位于大坝折坡高程以下时，降低库前水位对于大坝抗爆安全性能影响很小。

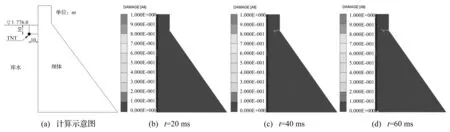
图10　库前水位位于大坝折坡处坝体损伤演化过程Fig.10 Damage evolution process of the dam when the water level is near the change in downstream slope

图11　库前水位位于大坝折坡以下10 m处坝体损伤演化过程Fig.11 Damage evolution process of the dam when the water level is below the change in downstream slope 10 m

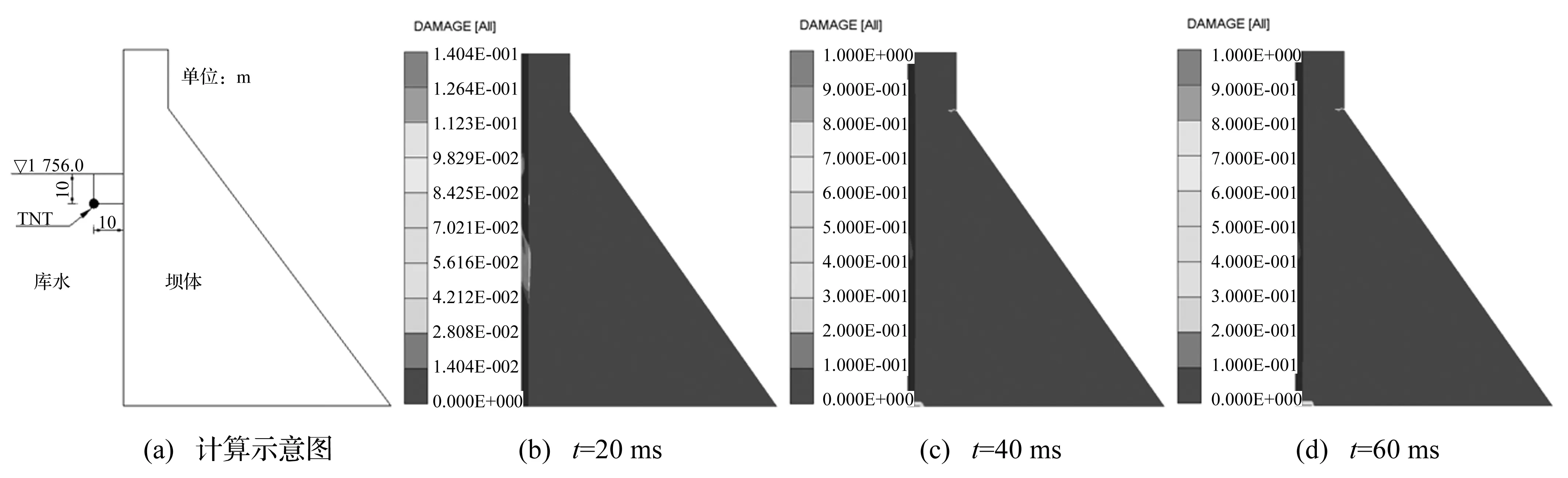
图12　库前水位位于大坝折坡以下20 m处坝体损伤演化过程Fig.12 Damage evolution process of the dam when the water level is below the change in downstream slope 20 m

图13给出了三种水位下坝顶上游面x方向速度-时间曲线。图中折坡处坝顶上游面速度峰值达到0.81 m/s，折坡以下10 m速度峰值约为0.62 m/s，折坡以下20 m速度峰值约为0.58 m/s。由此可知，随着库前水位的降低，大坝在爆炸冲击荷载作用下的动力响应会相应减弱，大坝抗爆安全性能得到一定程度的提高，并且当库前水位降低到折坡以下时，大坝的抗爆安全性能会有显著提高。

图13　坝顶上游面x方向速度曲线Fig.13 x-velocity of the upstream face of the dam crest

6结论

通过建立混凝土重力坝水下爆炸全耦合模型，分析不同库前水位下大坝在水下爆炸冲击荷载作用的损伤演化过程及抗爆安全性能，主要得出以下几点结论：

(1) 水下爆炸冲击荷载作用下，混凝土重力坝损伤破坏区域主要集中于大坝下游折坡处、正对炸药中心的大坝上游表面、自由水面与坝体交界处以及大坝坝踵处。其中大坝下游折坡处损伤破坏程度最为严重，为坝体抗爆薄弱部位，应加强对大坝下游折坡处的抗爆支护。

(2) 当库前水位降低到死水位时，大坝损伤破坏范围与正常蓄水位相比显著减小，通过研究对比工况下大坝损伤破坏情况，并分别与正常蓄水位、死水位下大坝损伤破坏情况对比分析，发现当爆心距和起爆深度相同时，大坝损伤破坏范围显著减小主要是由库前水位的降低造成的，而与起爆位置关系不大。

(3) 随着库前水位的降低，大坝损伤破坏范围逐渐减小，大坝抗爆安全性能得到提高，当水位降低到下游折坡处高程以下时，大坝抗爆安全性能得到显著提高。

参 考 文 献

[1] 王高辉,张社荣,卢文波,等.水下爆炸冲击荷载下混凝土重力坝的破坏效应Ⅰ:冲击波传播特性及损伤机理[J].水利学报,2015,46(2):723-731.

WANG Gao-hui, ZHANG She-rong, LU Wen-bo, et al. Damage effects of concrete gravity dams subjected to underwater explosion I:shock wave propagation characteristic and damage mechanism[J].Journal of Hydraulic Engineering, 2015,46(2):723-731.

[2] 张启灵,李波.高水位运行下近水面水下爆炸对拱坝结构的影响[J].应用力学学报,2013,30(2):153-160.

ZHANG Qi-ling, LI Bo.Impact on arch dam with a high reservoir level experiencing a near-surface underwater explosion shock loading[J].Chinese Journal of Applied Mechanics, 2013,30(2):153-160.

[3] Yu Tian-tang. Dynamical response simulation of concrete dam subjected to underwater contact explosion load[J]. Computer Science and Information Engineering, 2009,1(50): 769-774.

[4] Linsbauer H. Hazard potential of zones of weakness in gravity dams under impact loading conditions[J]. Frontiers of Architecture and Civil Engineering in China, 2011,5(1):90-97.

[5] 张社荣,王高辉,王超,等.水下爆炸冲击荷载作用下混凝土重力坝的破坏模式[J].爆炸与冲击,2012,32(5):502-507.

ZHANG She-rong, WANG Gao-hui, WANG Chao, et al. Failure mode analysis of concrete gravity dam subjected to underwater explosion[J].Explosion and Shock Waves, 2012,32(5):502-507.

[6] 张社荣,王高辉.水下爆炸冲击荷载作用下混凝土重力坝的抗爆性能[J].爆炸与冲击,2013,33(3):255-262.

ZHANG She-rong, WANG Gao-hui. Antiknock performance of concrete gravity dam subjected to underwater explosion[J]. Explosion and Shock Waves, 2013,33(3):255-262.

[7] Lu Lu, Li Xin, Zhou Jing. Protection scheme for concrete gravity dam acting by strong underwater shock wave[J]. Advanced Science Letters,2013,19(1):238-243.

[8] Malvar L J, Ross C A. Review of strain rate effects for concrete in tension[J].ACI Materials Journal,1999,96(5):614-616.

[9] Riedel W,Thoma K, Hiermaier S, et al. Penetration of reinforced concrete by BETA2B2500 numerical analysis using a new macroscopic concrete model for hyd-rocodes [C]//9th International Symposium, Interaction of the Effects of Munitions with Structures. Berlin,Germany: IBMAC, 1999:315-322.

[10] Holomquist T J, Johnson G R, Cook W H. A computational constitutive model for concrete subjective to large strains, high strain rates, and high pressures[C]//The 14th International Symposium on Ballistics. Quebec, Canada:American Defense Prepareness Association, 1993:591-600.

[11] Johnson G R. Computed radial stresses in a concrete target penetrated by a steel projectile[C]//Proceedings of the 5th International Conference On Structures under Shock and Impact.Portsmouth, UK,1998:793-806.

[12] Zhen Guo-tu, Yong Lu. Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations[J]. International Journal of Impact Engineering,2009,36:132-146.

[13] Livermore Software Technology Corporation. LS-DYNA keyword user’s manual[M]. Livermore,CA: Livermore Software Technology Corporation,2006.

[14] Zamyshlyaev Y. Dynamic loads in underwater explosion[M].Leningrad:Sudostroyeniye,1967.

[15] 范书立,陈明阳,陈健云,等. 基于能量耗散碾压混凝土重力坝地震损伤分析[J].振动与冲击,2011,30(4):271-275.

FAN Shu-li, CHEN Ming-yang, CHEN Jian-yun, et al. Seismic damage analysis of a concrete gravity dam based on energy dissipation[J]. Journal of Vibration and Shock,2011,30(4):271-275.

[16] 崔杰,杨文山,李世铭,等.近自由面水下爆炸冲击波切断效应研究[J].船舶力学,2012,16(5):465-471.

CUI Jie, YANG Wen-shan, LI Shi-ming, et al. Research on the cutoff effect of shock wave induced by underwater explosion near free surface[J]. Journal of Ship Mechanics,2012,16(5):465-471.

基金项目：国家自然科学基金资助项目(51125037);中央高校基本科研业务费专项资金项目(2042015KF0001)

收稿日期：2015-03-31修改稿收到日期：2015-08-05

通信作者王高辉 男，博士，讲师，1986年2月生

中图分类号:TV312

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.14.004

Influence of water level on the antiknock safety performance of concrete gravity dam

LI Qi, WANG Gao-hui, LU Wen-bo, CHEN Ming

(State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China)

Abstract:Through the early warning water discharge, not only the antiknock safety performance of dams can be effectively improved, but also the loss induced by dams failure can be reduced. The strain rate effect under blast loading was taken into consideration in the establishment of a fully coupled analysis model for gravity dams by using a dynamic analysis platform. The damage characteristics and antiknock safety performance of concrete gravity dams subjected to underwater explosion shock loading at normal water level and dead water level were analyzed contrastively. The dynamic response characteristics, the damage development process and the characteristics of spatial distribution of concrete gravity dams damage under different water level were analyzed in the early warning discharge condition. The results indicate that, for concrete gravity dam, with the reduction of water level in front of the dam, the damage range of dam decreases gradually, and that the antiknock safety performance of dam is improved remarkably when the water level in front of the dam decreases to the level of downstream slope.

Key words:concrete gravity dam; water level in front of dam; antiknock safety performance; fully-coupled model; underwater explosion; damage evolution

第一作者 李麒 男，硕士，1991年9月生