钢筋混凝土框架结构非线性静、动力分析的高效计算平台HSNAS(GPU)——Ⅱ验证分析

李红豫， 滕　军， 李祚华

(哈尔滨工业大学 深圳研究生院，深圳　 518055)



钢筋混凝土框架结构非线性静、动力分析的高效计算平台HSNAS(GPU)
——Ⅱ验证分析

李红豫， 滕军， 李祚华

(哈尔滨工业大学 深圳研究生院，深圳 518055)

摘要：利用GPU强大的并行计算能力，开发了一种结构非线性有限元静力、动力分析的高精度和高效率分析平台HSNAS(GPU)。为了验证所开发平台的计算精度和效率，分别对反复荷载作用下的钢筋混凝土构件层次和整体结构层次的拟静力试验以及典型框架结构的振动台试验进行模拟。结果表明HSNAS(GPU)平台得到的计算结果与试验结果吻合较好，该平台能较好地模拟构件轴力-弯矩-剪力的多维耦合效应以及刚度和强度退化等非线性行为，求解精度较高。与传统CPU计算平台相比，HSNAS(GPU)平台显示出12倍～ 14倍以上的加速效率。鉴于GPU的巨大计算潜能空间，所开发的计算平台为工程应用中大规模梁柱结构非线性有限元分析提供了高精度和高效率的分析手段。

关键词：钢筋混凝土；非线性分析；滞回性能；地震响应；加速比

土木工程结构有限元数值模拟属于相对计算密集型的问题，一般计算自由度可多达上千万，在传统CPU(Central Processor Unit，中央处理器)平台上完成计算任务，精度不高，耗时过多成为目前结构有限元模拟面临的瓶颈。近年来计算机图形处理器GPU(Graphics Processor Unit)的高速发展，基于GPU平台的高性能并行计算已经成为国内外研究的热点[1-3]。由于其硬件构造特殊，GPU的浮点运算、并行计算能力提供数十倍乃至于上百倍于CPU的性能，可以很好地解决大规模的科学计算问题[4]。因此，基于GPU并行计算能力，开发高精度和高效率的有限元分析平台，为解决目前结构数值模拟计算时间成本大的瓶颈提供一种新的思路[5]。

结构的分析模型和非线性求解算法开发是制约结构非线性分析应用的重要因素。纤维模型[6]已应用于钢筋混凝土梁柱结构有限元分析，但传统纤维模型单元刚度中忽略了剪切和扭转，亦或采用较为简化的材料本构，导致分析计算精度不高，因此如何弥补纤维模型上述不足，成为研究精细化分析模型需要解决的问题之一。其次，在求解结构非线性有限元静力、动力计算方法上，如何提高求解精度和效率，保证算法收敛性和稳定性，仍然存在许多需要深入研究的问题。

为此，本课题组在CPU串行与GPU并行相结合的异构架构上，提出了适用于GPU加速计算的有限元静力、动力算法，开发了GPU的线性方程组并行求解器和结构动力弹塑性时程分析软件，在纤维模型单元中引入扭转、剪切变形，采用精细化的非线性材料本构，建立了一种钢筋混凝土框架结构非线性有限元分析的高效计算平台HSNAS(GPU) (High-Rise Structure Nonlinear Analysis Software based on GPU)。

作者在上篇论文Ⅰ的研究基础上，采用多个适用于GPU计算的并行计算策略和优化策略，进一步提高了HSNAS(GPU)计算平台的执行效率。对多个钢筋混凝土构件和结构的非线性静力、动力试验进行模拟，验证了HSNAS(GPU)平台的计算精度。通过与传统CPU计算平台对比，HSNAS(GPU)获得了至少12倍～14倍以上的计算加速比，且随计算模型增大，加速效率将更加明显。基于GPU架构的进一步更新，HSNAS(GPU)的计算潜能将更加提高，必为结构非线性有限元分析提供一种高效实用的手段。

1GPU并行计算平台优化策略

1.1合并访问

当连续的16个线程同时进行全局存储器访问，如果内存地址满足对齐要求，则合并为同一访问，这样能有效提升访问速率[7]。本文的荷载向量、刚度矩阵等作为全局存储，但由于总刚矩阵的稀疏特性，不论是以行优先还是列优先存储，每个对角线上元素均是不连续的，且随着半带宽的变换，相距间隔较大，这样的存储方式将严重影响GPU的计算效率。为了满足GPU中数据合并访问要求，对总刚矩阵的存储方式进行改进，将二维数据存入一维数组中，使得GPU可同时处理的元素在一维数组中地址连续。同样的存储模式也应用于荷载(内力)向量、位移向量等。

1.2线程和线程块的划分技术

GPU中使用单指令多线程(Single Instruction Multiple Threads，SIMT)的执行模式[7]，每个SM (Streaming Multiprocessor)的SIMT单元处理一个线程块(block)中的32个线程(thread)，即32个thread会被组成一个线程束(warp)来一起执行；同一个warp里的thread，将会以不同的数据来执行同样的指令。因此在程序设计中，block大小应设置为32的整数倍。如果block中的线程数太少，空余线程闲置资源，浪费计算能力。反之，如果block中的线程数太多，各线程能够利用到的寄存器资源变少，则性能也将会下降。

因此，在划分线程和线程块的时候，不仅要考虑程序中的数据量参数，而且要考虑GPU架构的硬件参数。在目前现有的硬件架构中，每个线程块最多可有1024个线程。本文采用的GPU为基于GF104架构的NVIDIA Geforce GTX 460，含有7个SM，每个SM配置48个SP，当计算规模不大时，线程数量保持在32～128；当计算规模较大时，线程可逐渐增大到128～512。

1.3减少数据交互

对CPU与GPU通信进行优化，减少其数据交互，从而能降低通信时间。因此在GPU端执行核心计算任务，尽量让GPU与CPU之间的数据传输发生在核心计算任务的前后。在实际计算过程中，将多次的迭代循环划分成不同的步骤，每次由CPU向GPU提交一组循环计算，待GPU计算完成后将结果返回给CPU，然后再次进行下一组循环计算。

1.4程序的异步执行

当程序中不可避免地进行CPU和GPU之间反复大量的数据传输时，可以采用异步执行进行优化。异步执行是指程序在GPU进行数据拷贝的同时CPU就可接着执行程序中的下一步操作，从而实现CPU和GPU的并行计算。通过调用cudaMemcpyAsync()异步函数，不需要等待全部数据传输完毕，CPU就可以执行kernel的调用。这种采用“边拷贝边运算”的执行方式，可以有效隐藏CPU和GPU间数据传输时间，从而改善程序的整体性能。

除了上述优化策略，还包括为避免同一个warp中线程出现分支而在程序中减少分支判断语句；采用原子函数、CUBLAS库的优化函数实现更加复杂的算法；利用共享存储器和寄存器等优化策略。

2HSNAS(GPU)平台模拟分析

计算平台采用Intel i5-2300，频率为2.8 GHz，内存为4.00 GB的CPU和NVIDIA GeForce GTX 460的GPU搭建。GPU有336个流处理器核心，流处理器频率1.4 GHz，计算能力2.1，显存为1.0 GB，显存带宽为115.2 GB/s。软件程序采用Microsoft Visual Studio 2012开发环境和CUDA Fortran的PGI Accelerator Visual Fortran编译器，CUDA 5.0驱动。

2.1静力分析

2.1.1柱构件的拟静力试验模拟

选取美国太平洋地震研究中心钢筋混凝土柱抗震性能试验数据库(PEER-Structural Performance Database)中的低周反复荷载作用下矩形钢筋混凝土柱试验结果[8-13]，按照不同的破坏模式，分别选取了弯曲破坏、弯剪破坏、剪切破坏的柱构件试验。图1所示为试验模型和采用的截面配筋形式。表1列出了各试件的具体参数。

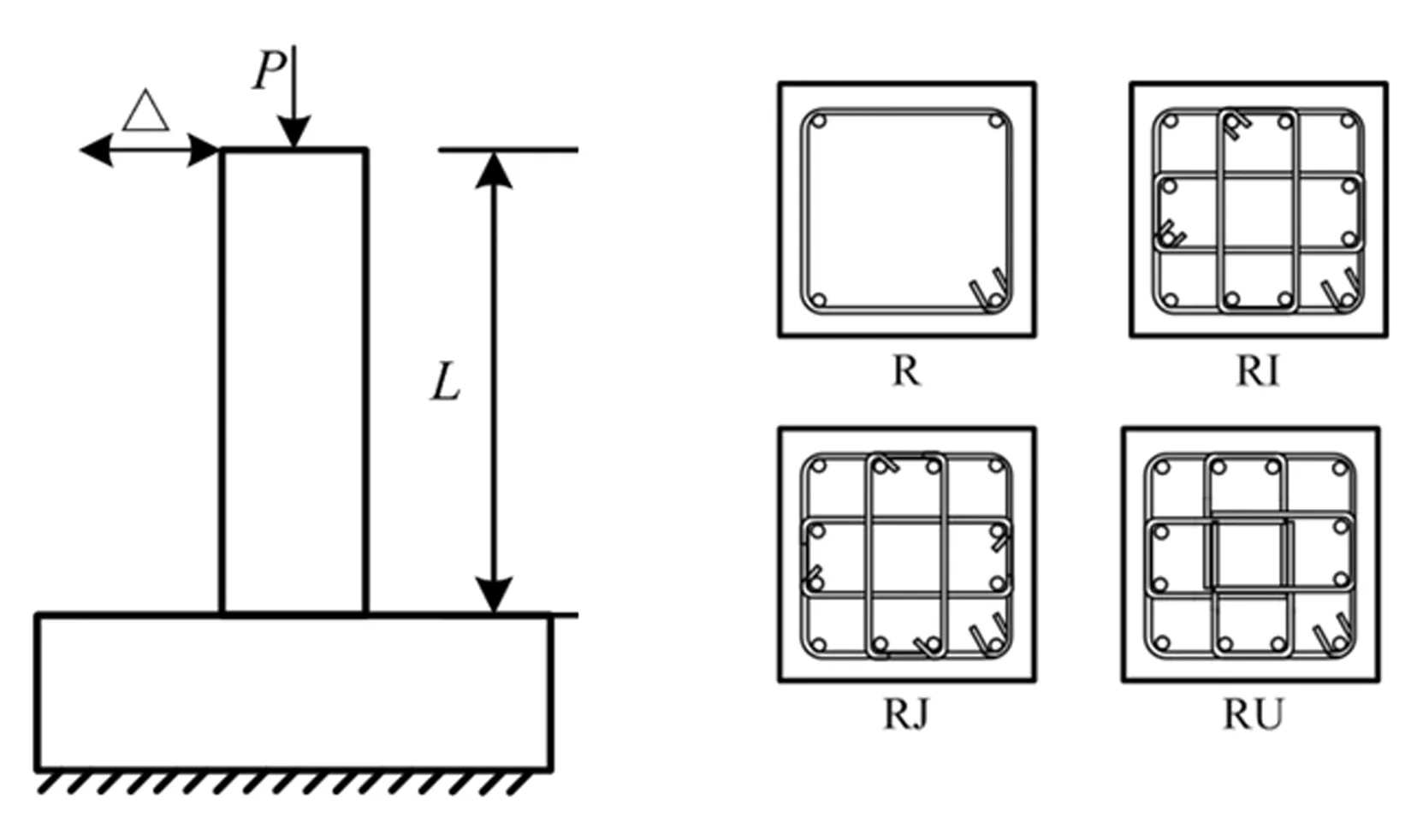
图1　试验模型和截面配筋形式Fig.1 Tested models and reinforcement details

序号试件轴压比截面尺寸/mm混凝土强度/MPa配箍形式柱高/mm破坏模式1ParkNo60.1550×55032.0RU1650弯曲2ParkNo70.3550×55032.1RJ1650弯曲3SaatciogluBG30.2350×35034.0RI1645弯曲4OnoCA025C0.26200×20025.8RI300弯剪5Nagasaka320.35200×20021.0R300弯剪6Ohue2D16RS0.14200×20032.0R400弯剪7ArakawaOA20.18180×18031.8R225剪切8ArakawaOA50.45180×18033.0R225剪切

HSNAS(GPU)平台的模拟计算采用位移加载，柱构件采用1～2个纤维单元模拟，每个单元采用5个Gauss-Labotto积分点，HSNAS(GPU)平台滞回曲线和骨架曲线的计算结果与试验结果对比如图2～图9所示。从图中看出计算得到的各级滞回环与试验吻合较好，能够较准确地反映反复荷载下柱构件的强度退化、刚度退化和滞回耗能等特性。从骨架曲线对比来看，计算得到的极限承载力与试验吻合较好，并且本文所采用的位移控制算法可以获得较满意的下降段。此外，对于不可忽略剪切变形的短柱(剪切破坏)，也能较精确地描述构件的非线性受力全过程。

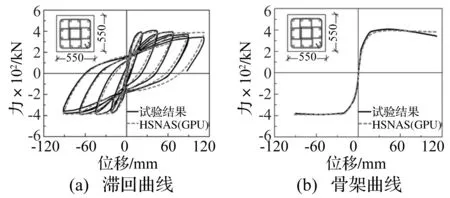
图2　试件Park No6计算对比(弯曲破坏)Fig.2 Comparison of column Park No6 (flexure failure)

图3　试件Park No7计算对比(弯曲破坏)Fig.3 Comparison of column Park No7 (flexure failure)

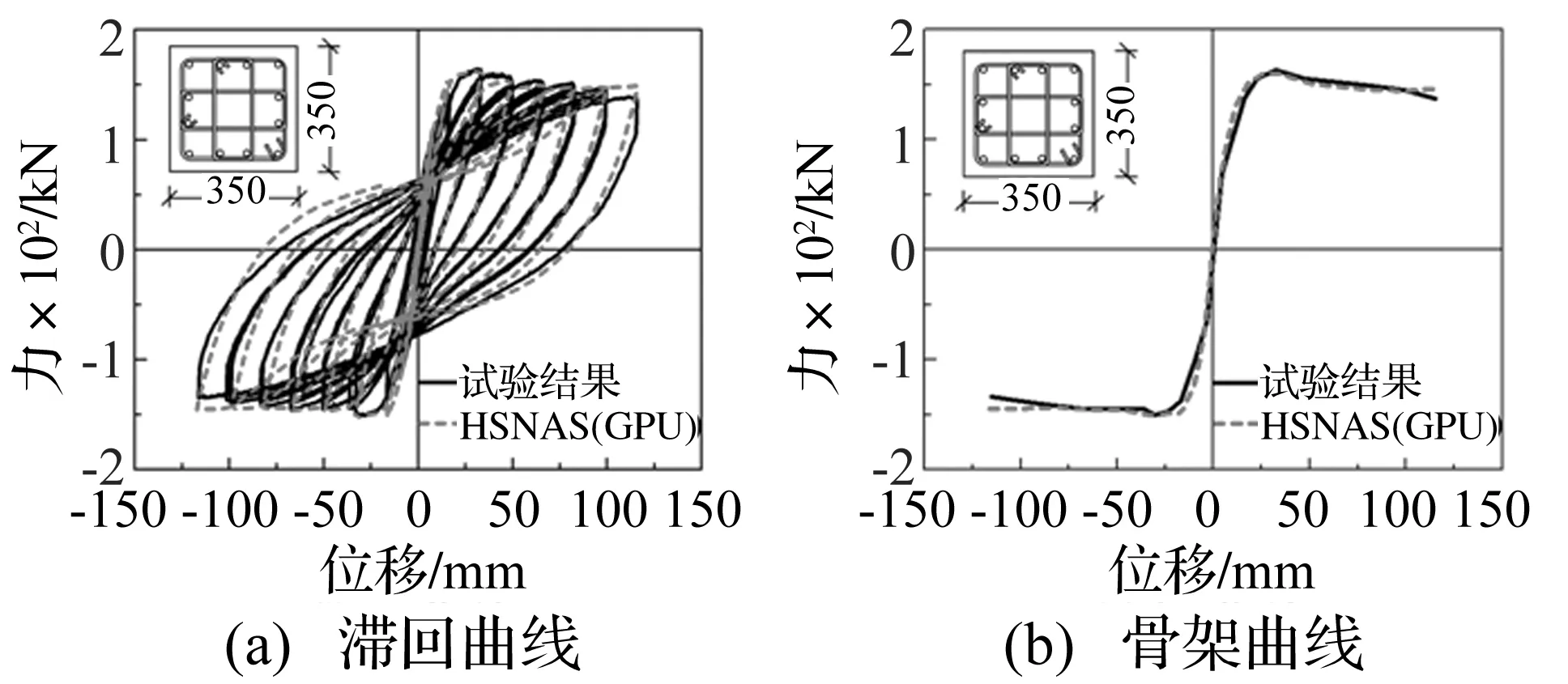
图4　试件Saatcioglu BG3计算对比(弯曲破坏)Fig.4 Comparison of column Saatcioglu BG3 (flexure failure)

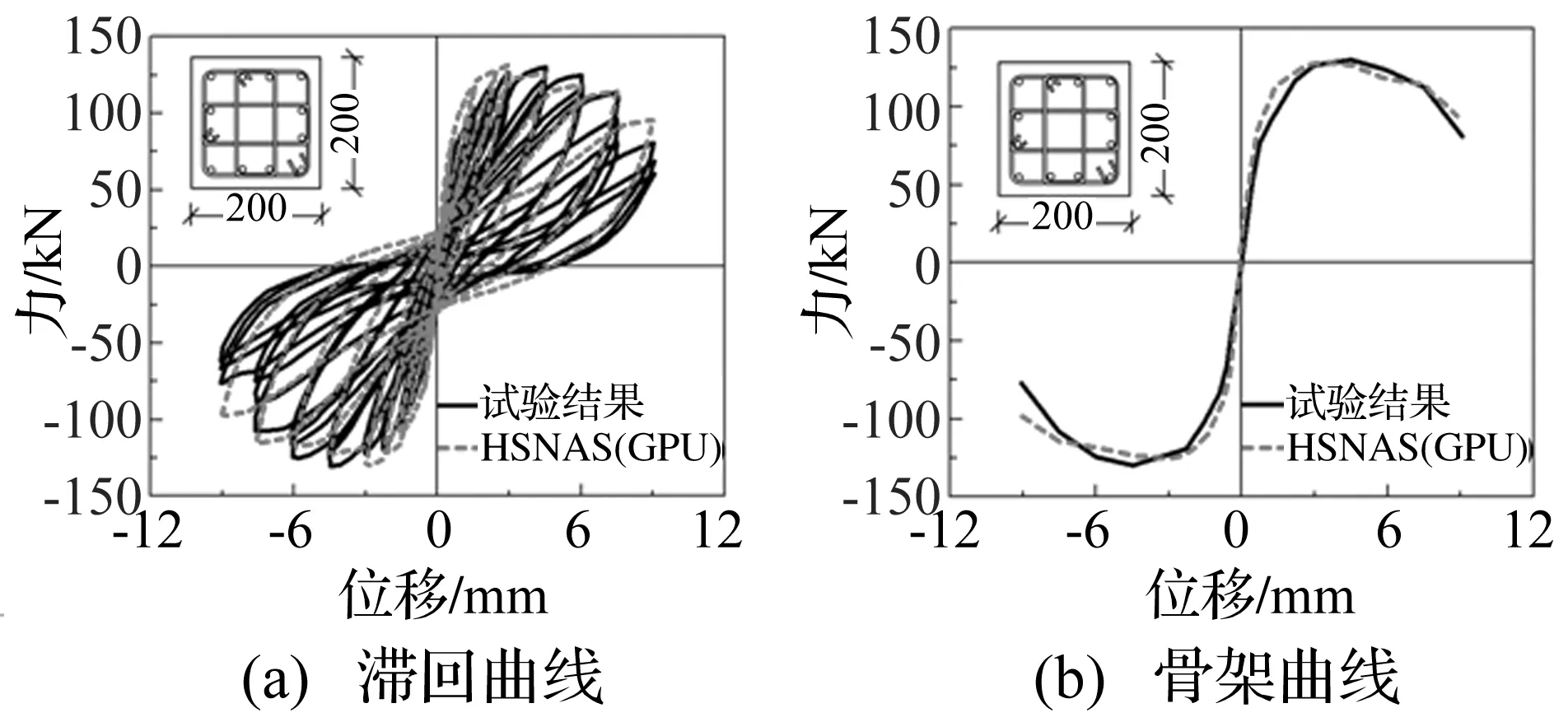
图5　试件Ono CA025C计算对比(弯剪破坏)Fig.5 Comparison of column Ono CA025C (flexure-shear failure)

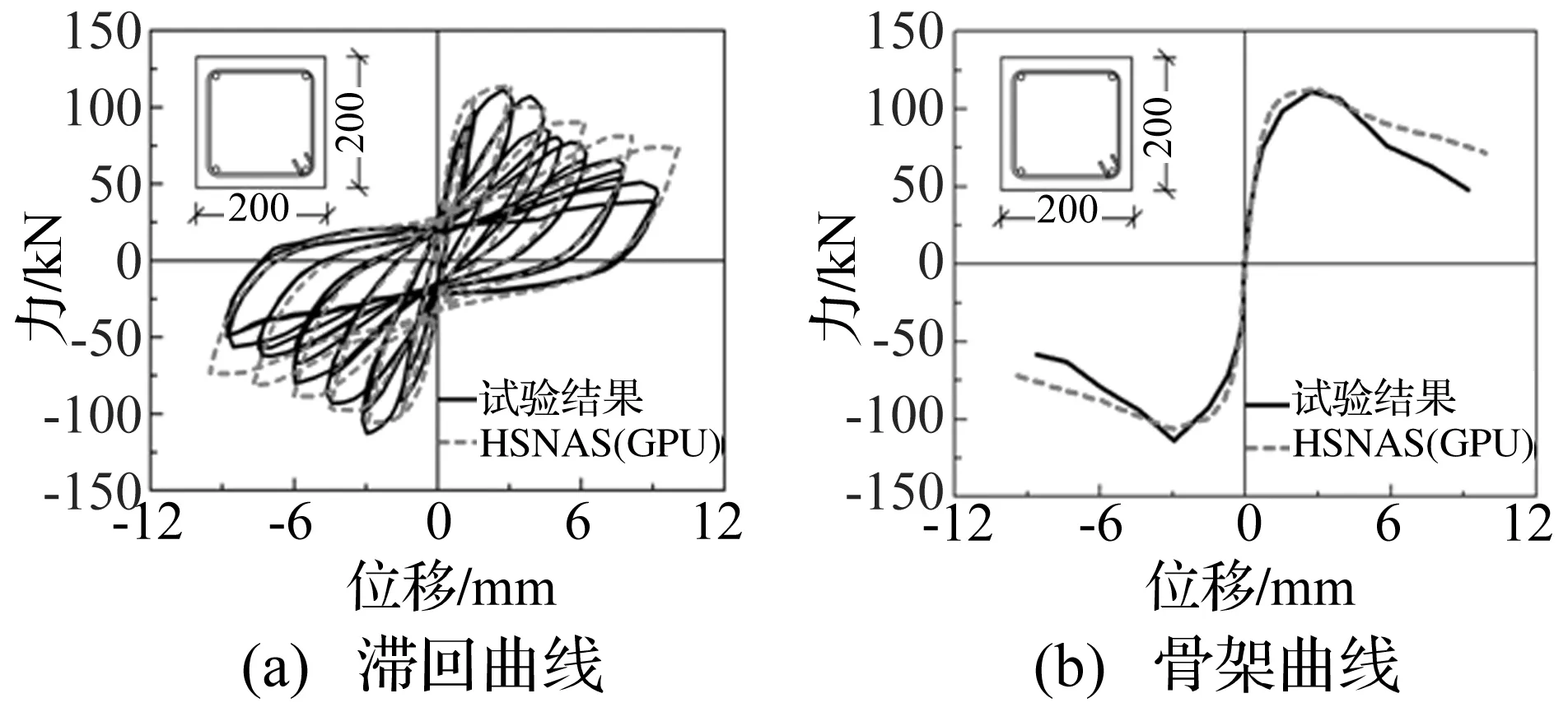
图6　试件Nagasaka 32计算对比(弯剪破坏)Fig.6 Comparison of column Nagasaka 32 (flexure-shear failure)

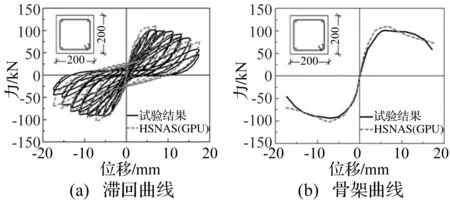
图7　试件Ohue 2D16RS计算对比(弯剪破坏)Fig.7 Comparison of column Ohue 2D16RS (flexure-shear failure)

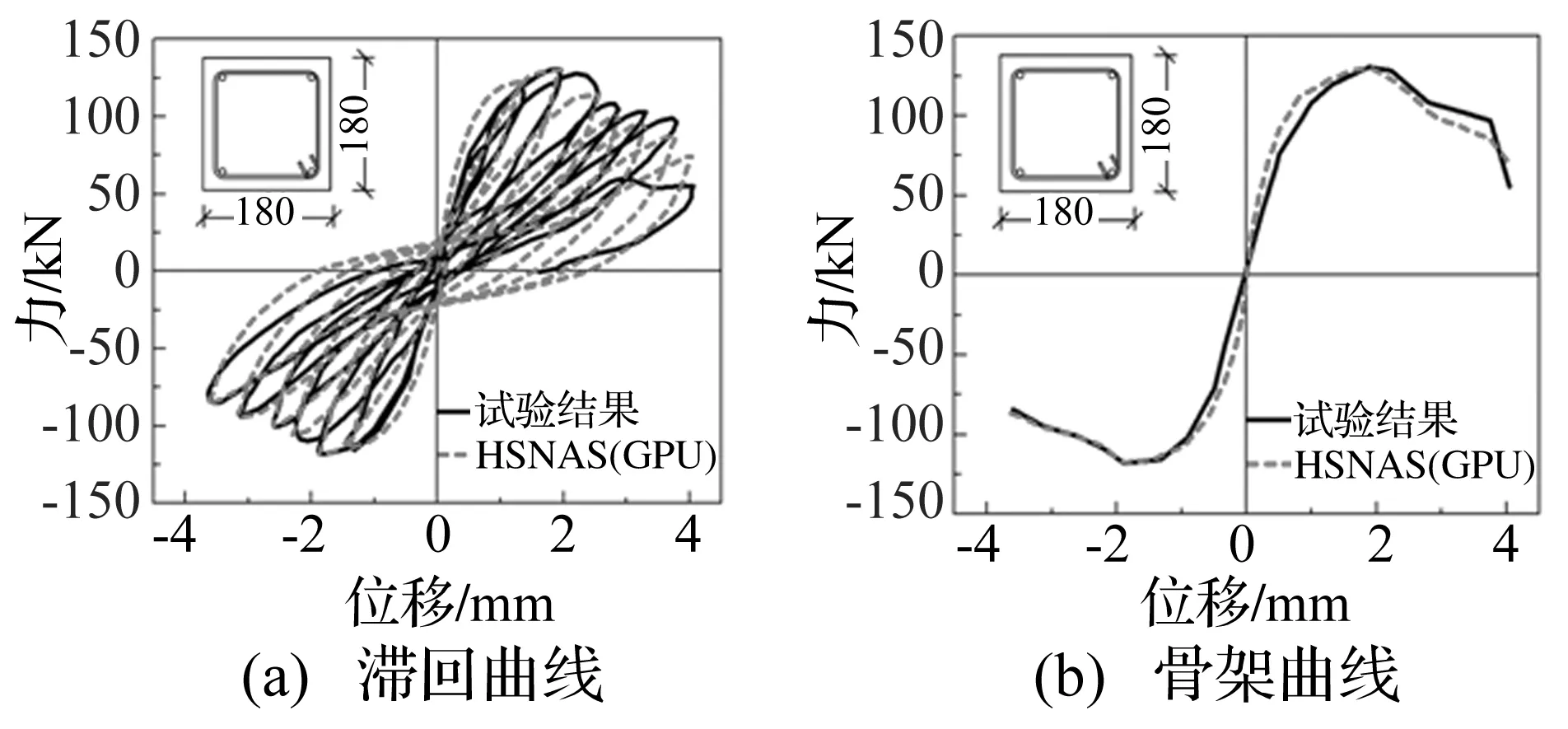
图8　试件Arakawa OA2计算对比(剪切破坏)Fig.8 Comparison of column Arakawa OA2 (shear failure)

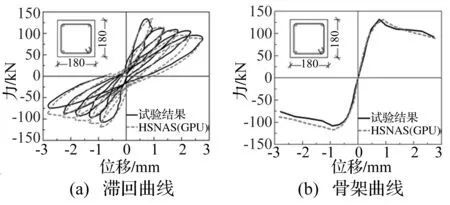
图9　试件Arakawa OA5计算对比(剪切破坏)Fig.9 Comparison of column Arakawa OA5 (shear failure)

2.1.2框架结构的反复荷载下的试验模拟

选取文献[14]的一榀三层两跨平面框架结构的低周反复加载试验。钢筋混凝土框架结构模型和截面配筋如图10所示，材料参数如表2所示。

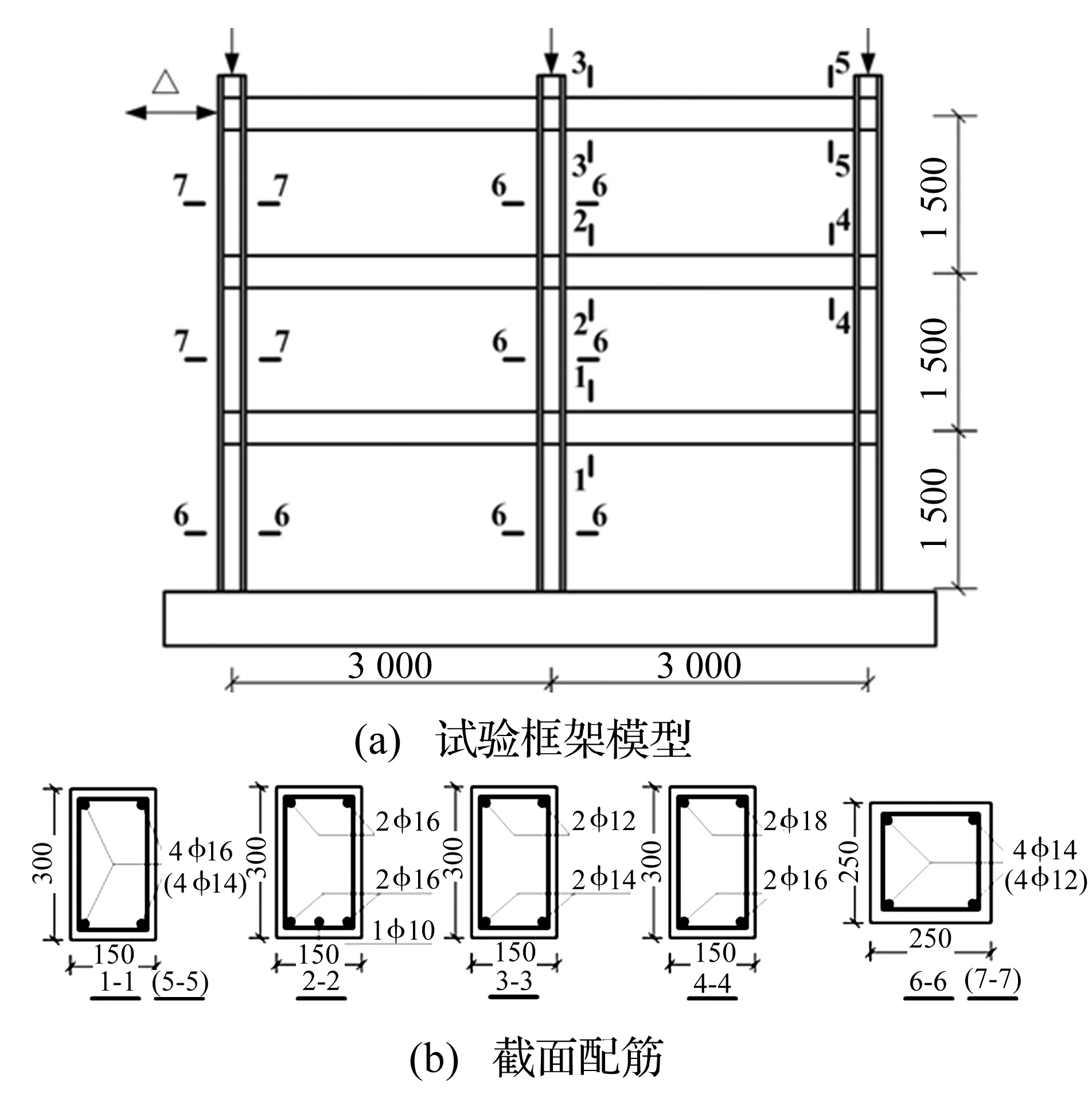
图10　试验框架模型和截面配筋Fig.10 Frame model and reinforcement details

在HSNAS(GPU)平台上模拟过程中，分别在框架中柱和边柱的柱顶施加500 kN和300 kN的恒定竖向压力，框架顶层梁处施加侧向水平位移，位移增量步设置为0.5 mm。图11给出了HSNAS(GPU)平台计算获得的滞回曲线和骨架曲线与试验结果对比。由图中看出，峰值点前，计算结果与试验结果吻合较好，峰值点后的下降段，试验有较强的强度退化和捏拢效应，而模拟尚未考虑钢筋和混凝土之间的黏结滑移作用，因此计算结果与试验结果略有差别。但是综合对比滞回曲线和骨架曲线的峰值点、刚度退化和滞回特性，表明HSNAS(GPU)平台具有较高的求解精度。

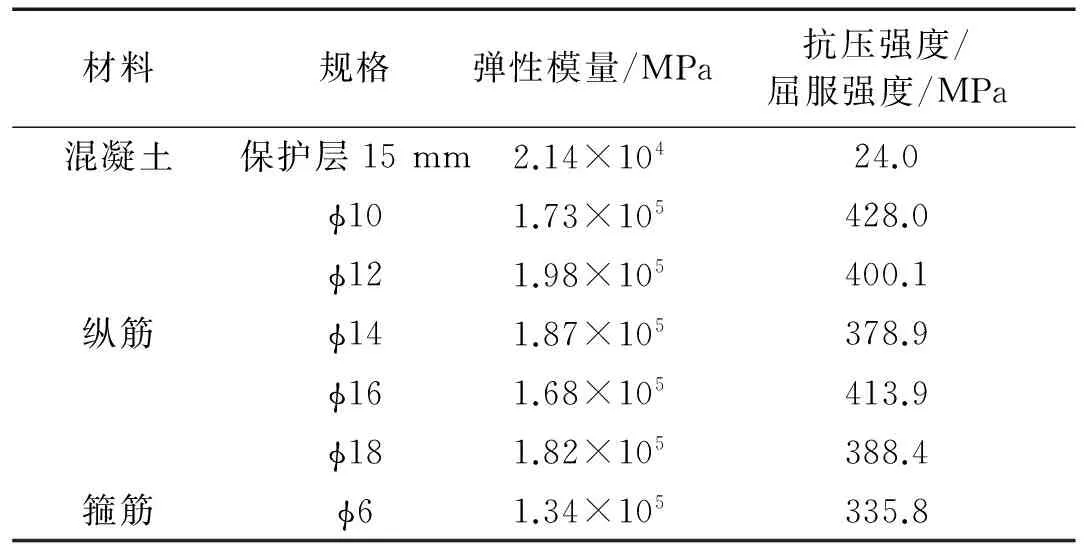
表2　钢筋混凝土框架材料参数

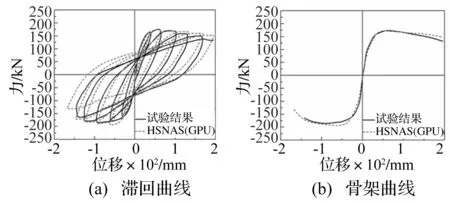
图11　框架模型在反复荷载作用下的计算对比Fig.11 Comparison of the static cyclic response of frame model

2.2动力分析

选取文献[15]的一栋12层钢筋混凝土框架结构的振动台模型试验，模型比例1/10。标准层每层配重19.4 kg，屋面层19.7 kg。结构模型如图12所示，材料参数如表3所示。

HSNAS(GPU)平台计算得到的动力特性与试验结果对比如表4所示，动力特性计算偏差在3.5%以内，表明计算模型能较好地反映试验模型的动力特性。El-Centro波地震波峰值为35 gal和200 gal的顶层加速度时程曲线对比如图13所示。由图中看出，在35 gal工况作用下，结构基本保持弹性状态，计算结果与试验结果吻合较好，但在200 gal工况作用下，计算结果与试验结果出现偏差。分析主要原因是试验随着振动次数增加和输入激励的加速度峰值增大，框架结构出现损伤，刚度退化严重，导致结构呈非线性响应。因此为了考虑前次地震输入累积对本次地震反应所造成的影响，本文采用连续接力的计算方式，按照试验的工况顺序进行模拟，表5给出各工况下框架模型频率计算结果。由表5知，200 gal工况下，频率相对于初始降低幅度较大，表明框架结构已经受到较严重的损伤。在修正了框架模型频率之后，计算得到的顶层加速度时程曲线(如图14所示)与试验结果较为吻合。图15给出层间位移角的对比，从图中看出，层间位移角沿高度方向的分布较为吻合，且均在4～6层处达到最大值。综合以上分析，说明HSNAS(GPU)平台的非线性时程分析能够较好地描述结构的线性和非线性动力响应。

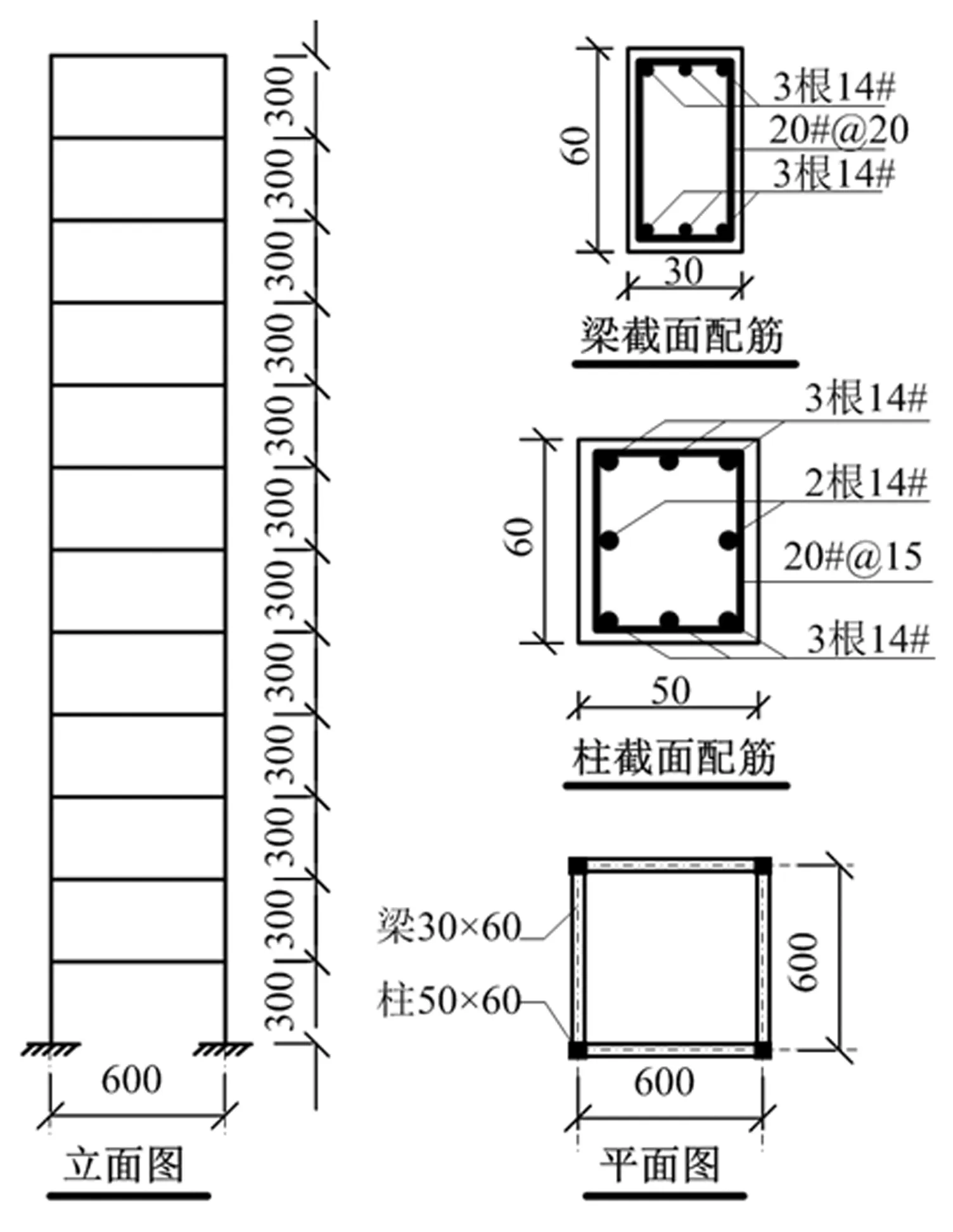
图12　试验框架模型和截面配筋形式Fig.12 Frame model and reinforcement details

材料规格弹性模量/MPa抗压强度/屈服强度/MPa微粒混凝土1～2F8.490×1037.9693～4F7.062×1035.7355～6F7.649×1037.4027～8F7.917×1037.6699～10F7.322×1037.20211～12F8.065×1038.202铁丝14#1.90×10539120#1.90×105327

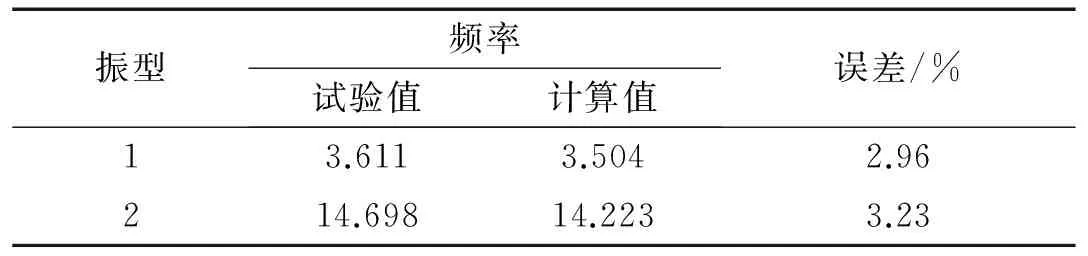
表4　动力特性对比

图13　顶层加速度响应对比Fig.13 Comparison of top story acceleration

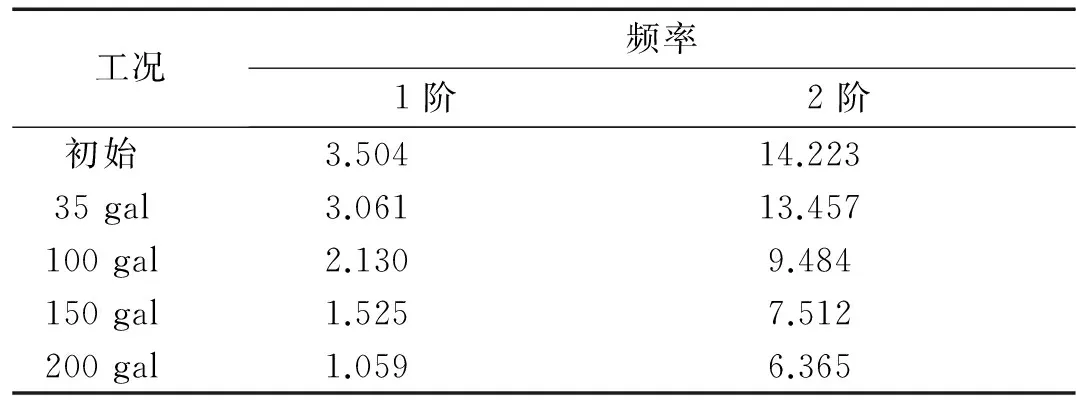
Hz

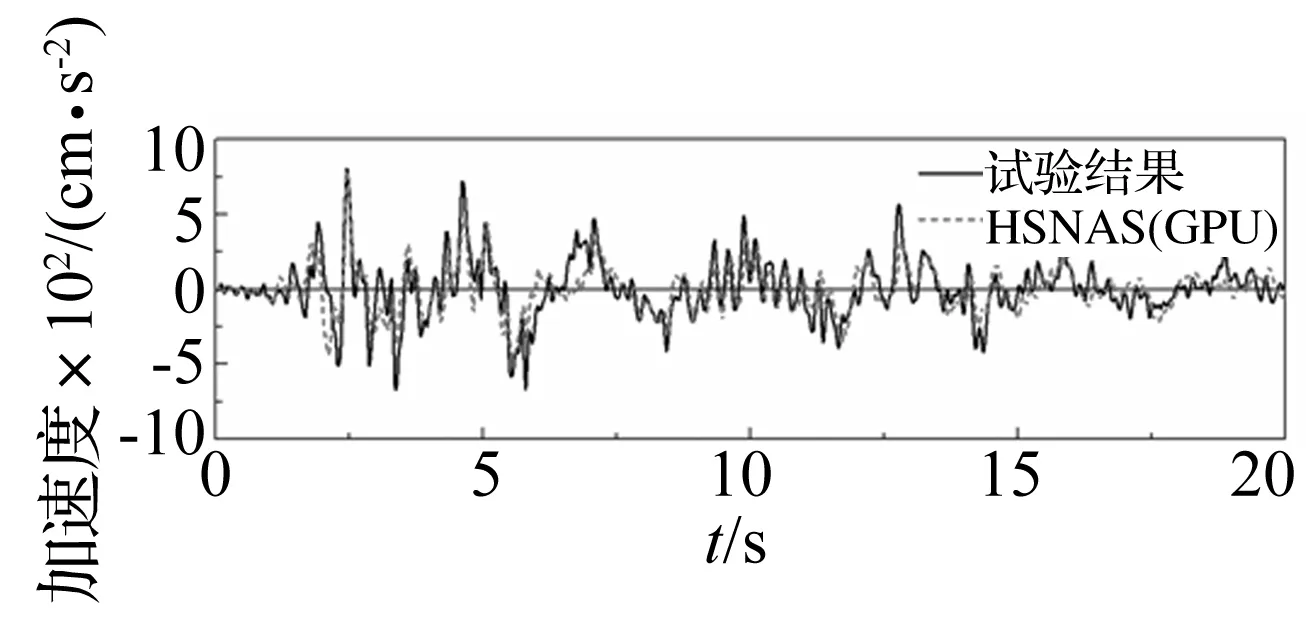
图14　模型修正后顶层加速度响应对比(El-Centro波200 gal)Fig.14 Comparison of top story acceleration of revised model

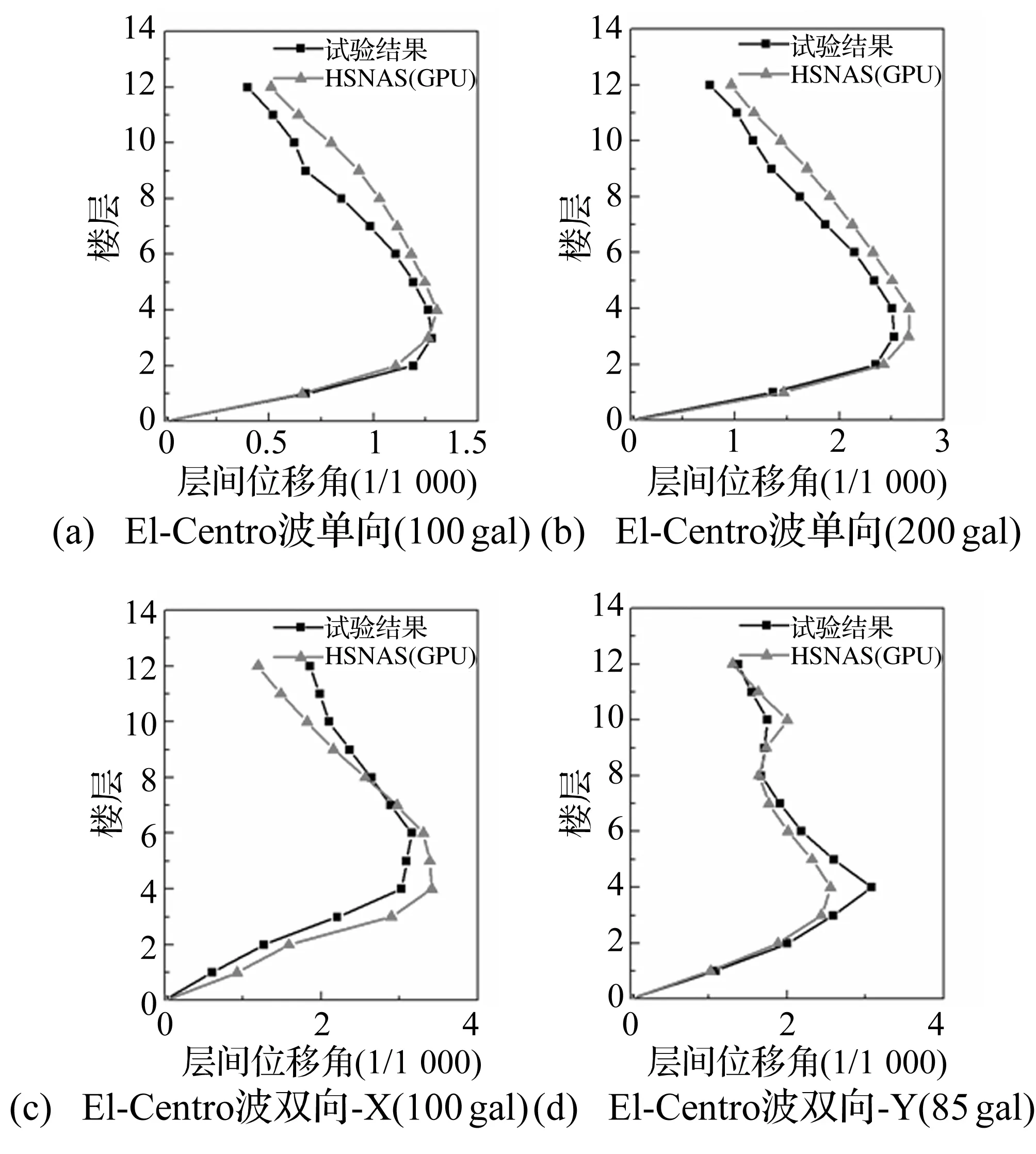
图15　层间位移角对比Fig.15 Comparison of inter-floor drift ratio

3HSNAS(GPU)平台的计算效率

3.1静力问题

为了研究HSNAS(GPU)平台的计算效率，分别测量HSNAS(GPU)平台和传统CPU串行平台的计算耗时，采用加速比来衡量平台计算速度所能得到的加速倍数[4]。表6给出框架有限元模型的单元划分。图16给出框架划分规模分别与计算时间及加速比的关系，由图16知，模型划分单元数越大，HSNAS(GPU)平台计算效率相比CPU平台也越高，自由度数1 782时加速比为14倍。

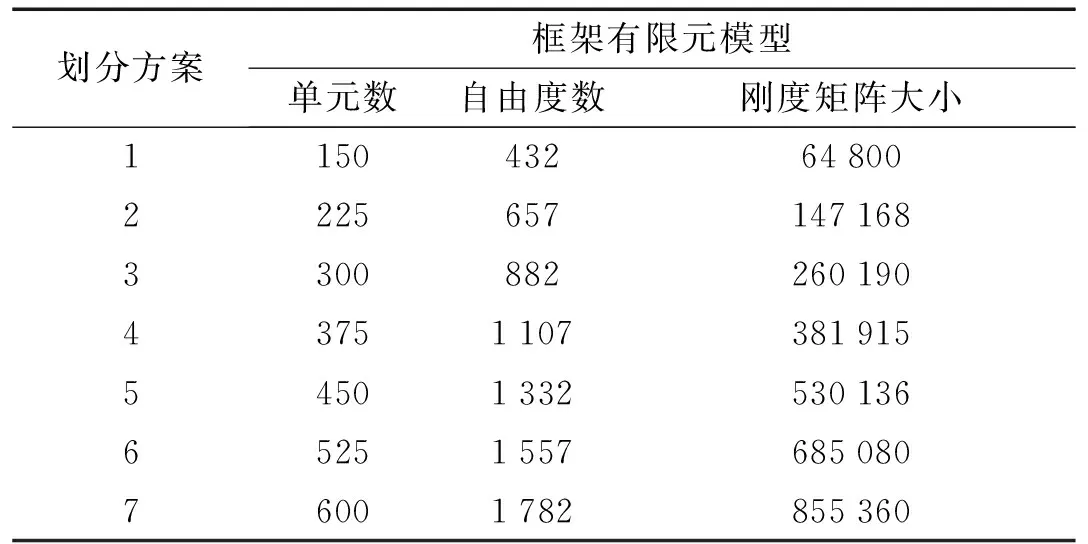
表6　静力计算框架模型大小

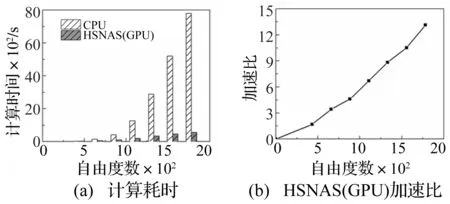
图16　单个位移增量步计算耗时及加速比Fig.16 Comparison of computation time and speed up for one incremental displacement-step

3.2动力问题

分析模型单元划分如表7所示。动力计算相对于静力计算耗时更多，因此分别统计Newmark法单个时间步下的PCG线性方程组并行求解器耗时，与Newmark法10个时间步下的计算耗时，分别计算其加速比，分析结果见图17和图18。从图17看出，采用GPU的线性方程组并行求解器，能够较大程度地减少方程组的求解时间，当模型自由度为7 500时，获得了25倍的加速效率。从图18看出，Newmark法中10个时间积分步的加速比为12倍，不及每个时间步内求解方程组25倍的加速效率。这是因为在每一个时间步开始和结束时，数据需要在CPU和GPU之间进行传输，这样的数据传输相对GPU的直接访问是缓慢的，因此数据通信需要耗掉一定时间。但是随着模型的计算规模增大，GPU和CPU之间的通信时间占总时间将逐渐减少。此外，在传统CPU计算平台对一个10 800自由度数的框架结构模型进行了大震弹塑性动力响应分析，整个计算耗时需要将近两天半时间，而采用本文开发的HSNAS(GPU)平台，只需5个小时就能完成计算，可见本平台对减小时间成本具有较大优势。

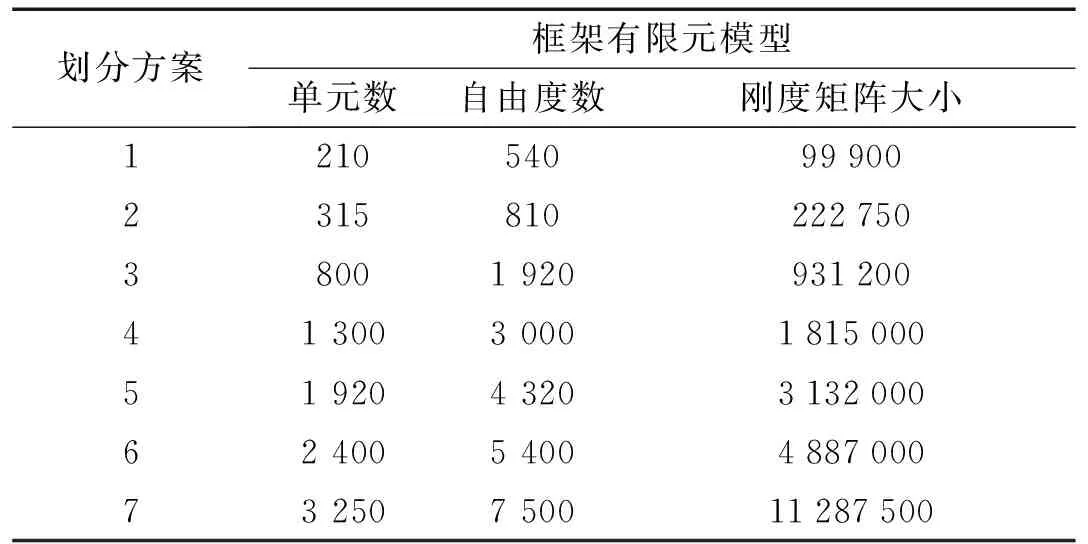
表7　动力计算框架模型大小

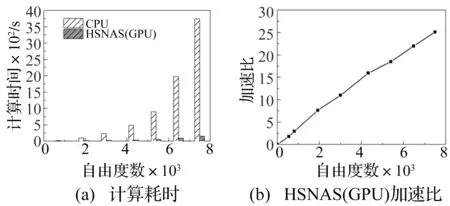
图17　单个时间步的PCG求解器计算耗时及加速比Fig.17 Comparison of computation time and speed up for PCG solver in one time-step

图18　Newmark法10个时间步的计算耗时及加速比Fig.18 Comparison of computation time and speed up for ten time-steps of Newmark-beta method

4结论

本文利用GPU强大的并行计算能力，开发了结构非线性有限元静力、动力分析的高精度和高效率分析平台HSNAS(GPU)，对该平台进行了计算精度和效率分析，获得了以下结论：

(1) HSNAS(GPU)平台上可有效地模拟低周反复荷载条件下钢筋混凝土结构的非线性滞回性能，模拟得到的滞回关系曲线、骨架曲线与试验结果吻合较好，能够较好地考虑构件的刚度退化和强度退化等效应并且获得了较满意的下降段，对于横向剪切变形不可以忽略的短柱等构件，也能较准确地描述其非线性性能。

(2) HSNAS(GPU)平台上可有效地模拟钢筋混凝土结构的非线性地震响应，通过与振动台试验对比表明计算精度较高。

(3) 在HSNAS(GPU)平台上对钢筋混凝土框架结构进行非线性静力和动力分析的计算效率研究，分别获得了14倍和12倍以上的提速效率。在并行前提条件相同的情况下，模型越复杂，计算数据越庞大，GPU的加速比会越高。因此可以证明，鉴于GPU的巨大计算潜能空间，本文开发的HSNAS(GPU)平台，可在规模更大更复杂的框架计算模型中推广应用。

参 考 文 献

[1] Barreiro A, Crespo A J C, Domínguez J M, et al. Smoothed particle hydrodynamics for coastal engineering problems [J]. Computers & Structures,2013, 120: 96-106.

[2] Chetverushkin B N, Shilnikov E V, Davydov A A. Numerical simulation of the continuous media problems on hybrid computer systems [J]. Advances in Engineering Software, 2013, 60/61: 42-47.

[3] Bryan B A. High-performance computing tools for the integrated assessment and modelling of social-ecological systems[J]. Environmental Modelling & Software, 2013, 39: 295-303.

[4] 刘小虎, 胡耀国, 符伟. 大规模有限元系统的GPU加速计算研究[J]. 计算力学学报, 2012, 29(1): 146-152.

LIU Xiao-hu, HU Yao-guo, FU Wei. Solving large finite element system by GPU computation [J]. Chinese Journal of Computational Mechanics, 2012, 29(1): 146-152.

[5] 李红豫, 滕军, 李祚华. 基于CPU-GPU异构平台的高层结构地震响应分析方法研究[J]. 振动与冲击,2014,33(13): 86-91.

LI Hong-yu, TENG Jun, LI Zuo-hua. Analysis method for seismic response of high-rise structure based on CPU-GPU heterogeneous platform [J]. Journal of Vibration and Shock,2014,33(13): 86-91.

[6] Spacone E. Flexibility-based finite element models for the nonlinear static and dynamic analysis of concrete frame structures [D]. Berkeley,CA:University of California, 1994.

[7] 张舒, 褚艳利. GPU高性能运算之CUDA[M]. 北京：中国水利水电出版社，2009.

[8] Tanaka H, Park R. Effect of lateral confining reinforcement on the ductile behavior of reinforced concrete columns [R]. Christchurch, New Zealand： University of Canterbury, 1990.

[9] Saatcioglu M, Grira M. Confinement of reinforced concrete columns with welded reinforcement grids [J]. ACI Structure Journal, 1999, 96(1): 29-39.

[10] Ono A, Shirai N, Adachi H, et al. Elasto-plastic behavior of reinforced concrete column with fluctuating axial force [J]. Transactions of the Japan Concrete Institute, 1989, 11:239-246.

[11] Nagasaka T. Effectiveness of steel fiber as web reinforcement in reinforced concrete columns [J]. Transactions of the Japan Concrete Institute, 1982, 4:553-560.

[12] Ohue M, Morimoto H, Fujii S, et al. The behavior of RC short columns failing in splitting bond-shear under dynamic lateral loading [J]. Transactions of the Japan Concrete Institute, 1985, 7:293-330.

[13] Arakawa T, Arai Y, Mizoguchi M, et al. Shear resisting behavior of short reinforced concrete columns under biaxial bending-shear [J]. Transactions of the Japan Concrete Institute, 1989, 11:317-324.

[14] 徐云扉, 胡庆昌, 陈玉峰, 等. 低周反复荷载下两跨三层钢筋混凝土框架受力性能的试验研究[J]. 建筑结构学报, 1986, 7(2): 1-16.

XU Yun-fei, HU Qing-chang, CHEN Yu-feng, et al. The experimental study of the behavior of a two-bay three-story RC frame under cyclic loading [J]. Journal of Building Structures, 1986, 7(2): 1-16.

[15] 吕西林, 李培振, 陈跃庆. 12 层钢筋混凝土标准框架振动台模型试验的完整数据[R]. 同济大学土木工程防灾国家重点实验室振动台试验室, 2004.

基金项目：国家自然科学基金重大国际(中美)合作研究项目(5126112037)；国家自然科学基金面上项目(51278155;51378007)

收稿日期：2015-04-07修改稿收到日期：2015-07-07

通信作者李祚华 男，博士，副教授，1978年生

中图分类号:TU375

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.14.009

An efficient platform HSNAS(GPU) for nonlinear static and dynamic analysis of reinforced concrete frames—Ⅱ. Program verification and analysis

LI Hong-yu, TENG Jun, LI Zuo-hua

(Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, China)

Abstract:A simulation platform HSNAS(GPU) for nonlinear static and dynamic analysis based on the parallel computing ability of the graphics processing unit (GPU) was developed. In order to verify the precision and efficiency of the HSNAS(GPU), static cyclic loading tests and a shaking table test on reinforced concrete (RC) columns and frames were simulated using the platform HSNAS(GPU). The results of HSNAS(GPU) show a good agreement with the results of tests. Considering the strength/stiffness degradation and the coupling effects among axial force, shear force, and bending moment, the complicated nonlinear behavior of RC columns can be simulated effectively and precisely. The static and dynamic analyses using the developed platform HSNAS(GPU) achieve a speedup of 12-14 times in computation compared with the traditional serial platform. Based on exploiting the potential of GPU computation, the platform HSNAS(GPU) could provide a computation scenario with high accuracy and efficiency for the large-scale nonlinear analysis of reinforced concrete frames.

Key words:reinforced concrete; nonlinear analysis; hysteretic behavior; earthquake response; speedup

第一作者 李红豫 女，博士生，1985年生