有限长线接触混合润滑特性研究

刘明勇， 刘怀举， 朱才朝， 王　雷

(1.湖北工业大学 湖北省农业机械工程研究设计院，武汉 430068； 2. 重庆大学 机械传动国家重点实验室，重庆　400044)



有限长线接触混合润滑特性研究

刘明勇1， 刘怀举2， 朱才朝2， 王雷1

(1.湖北工业大学 湖北省农业机械工程研究设计院，武汉 430068； 2. 重庆大学 机械传动国家重点实验室，重庆400044)

摘要：选择规则表面粗糙度分布，建立了有限长线接触混合润滑模型，数值模拟粗糙度幅值、波长、方位角和工况变化对润滑特性的影响。结果表明：建立的数学模型在较宽工况范围内具有良好的适应性；随着粗糙度波长增大，接触线中部首先发生润滑状态改变，说明增大粗糙度波长有益于改善润滑；随着粗糙度幅值增大，压力波动剧烈，边缘效应更加显著；工况变化对润滑状态影响明显，其中在润滑状态转换区域的润滑特征参数变化显著；随着粗糙度方位角的变化，润滑特征参数呈现周期性波动，当方位角为0°时润滑状态最佳，方位角为45°时润滑状态最差。

关键词：有限长线接触；混合润滑；粗糙度；方位角

摩擦和磨损广泛存在于接触副表面，如齿轮、轴承、凸轮等，研究人员开展了大量有关工程接触副的摩擦学研究[1-4]。现有工程接触副的摩擦学研究多采用线接触模型，这对截面几何与运动学参数变化的接触副误差较大。随着现代工业装备向高速重载方向发展，接触副通常处于混合润滑状态，需建立有限长线接触模型，以便考虑表面粗糙度纹理对接触疲劳寿命影响。

在有限长线接触的摩擦学研究与工程应用方面，学者们做了许多有益的工作。Mostofi等[5]首次研究了轻/中载工况时，端部修形对圆柱滚子弹流润滑影响；徐文等[6]研究了有限长直母线滚子副的边缘效应和断泄对润滑成膜能力的影响；Liu等[7]首次研究了有限长线接触的热效应并与等温解对比分析；孙浩洋等[8]研究了重载工况下有限长线接触圆柱滚子的修形参数和工况对成膜能力的影响；Ren等[9]研究了3D粗糙表面的线接触混合润滑，并忽略了端泄的影响；华同曙等[10]实验研究摆动频率对圆柱滚子润滑特性的影响；陈芳华等[11]研究了对数修形圆锥滚子的弹流润滑特性，获得接触副的压力、膜厚和Mises应力分布；王文中等[12]采用有限长线接触理论，建立斜齿轮瞬态弹流润滑模型，揭示完整啮合周期内的等温润滑特性；Zhu等[13]研究了圆柱滚子的几何参数和工况对弹流润滑影响，并初步研究了混合润滑模型；Mihailidis等[14]研究了有限长线接触的非牛顿乏油润滑，并讨论工况与端部修形对润滑影响。

上述研究中，接触面大多数为理想光滑表面，部分文献开展了粗糙度表面的润滑研究，尚未进行系统研究，仍有许多问题亟待解决。鉴于有限长线接触区别于点、线接触，结合工程接触副的特点，有必要开展有限长线接触混合润滑的进一步研究。

1数学模型

1.1几何模型

润滑接触分析中，有限长圆柱滚子可等效为圆柱体和平面接触，接触线端部采用相切圆弧修形，以保证几何连续性和消除应力集中，如图1所示。

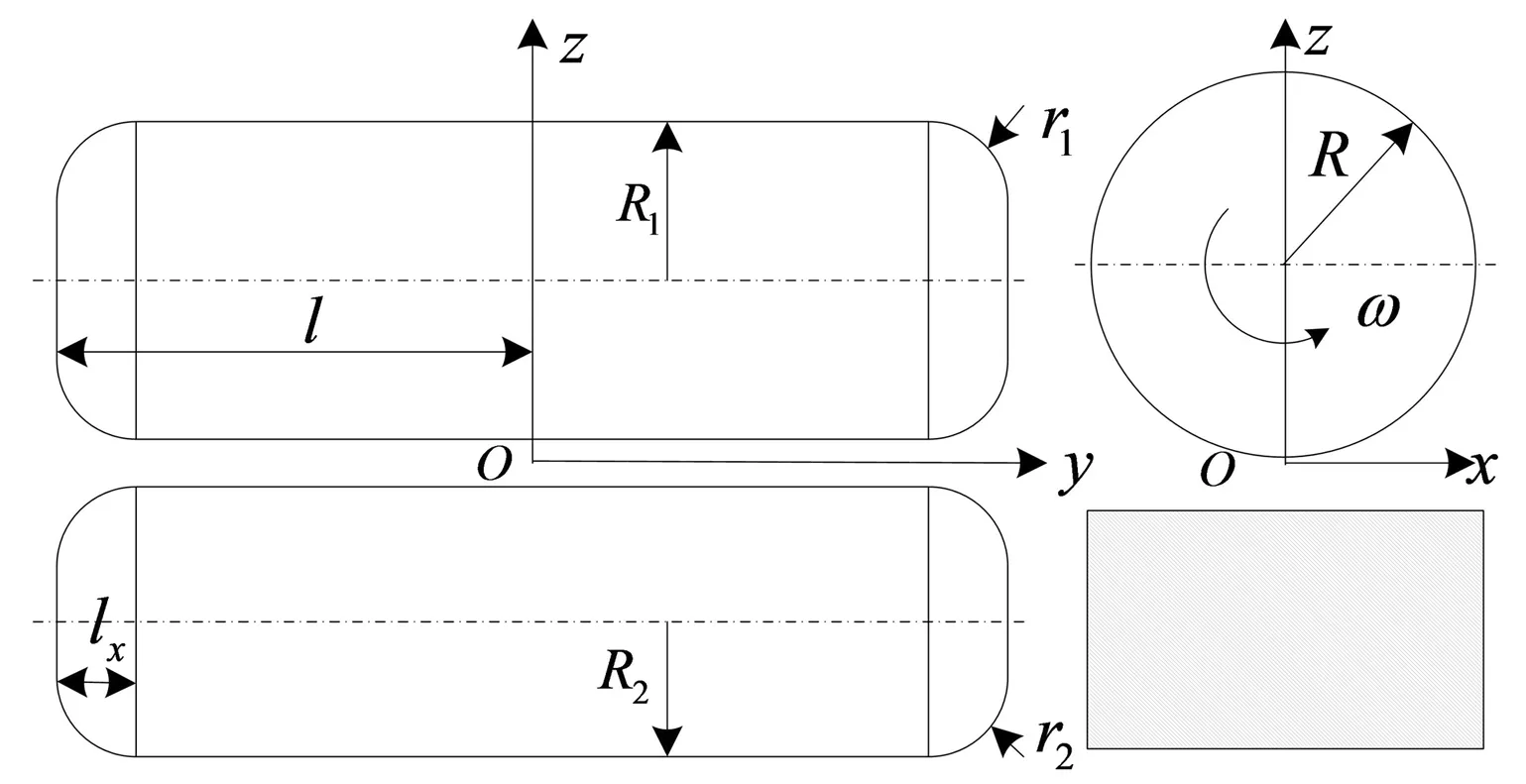
图1　有限长线接触润滑模型Fig.1 A finite line contact lubrication model

接触副的润滑几何间隙为：

直母线部分

hg=x2/2R1+x2/2R2=x2/2R

(1a)

端部修形部分

hg=x2/2R+y2/2r

(1b)

式中：1/R=1/R1+1/R2，1/r=1/r1+1/r2。

1.2润滑控制方程

基于Hu-Zhu[13]统一Reynolds方程建立有限长线接触混合润滑模型，并考虑流体非牛顿特性。

流体润滑区

(2a)

干接触区

(2b)

式中：ue为卷吸速度，ρ为油膜黏度，t为时间变量，p,h为压力和膜厚，干接触膜厚截断值εh=10-6。

考虑流体的剪切稀释效应，引入等效黏度η*。忽略膜厚方向黏度变化，Eyring流体的等效黏度可表示为：

(3)

式中：τx为接触面沿x轴剪切力，τ0为流体特征剪切力，η为流体黏度。

润滑膜厚由刚体位移h0(t)、几何间隙hg、表面粗糙度s(x,y,t)和弹性变形v(x,y,t)组成：

h(x,y,t)=h0(t)+hg(x,y)-

s(x,y,t)+v(x,y,t)

(4)

选取规则正弦表面粗糙度函数进行分析：

(5)

式中：Am为粗糙度幅值，λx、λy为沿x，y方向粗糙度波长，xd代表粗糙度参考点位置且xd=xs+u1t。

润滑油黏度与密度分别采用Roelands黏压关系和Dowson-Higgison密压关系式：

η=η0exp{(lnη0+9.67)[-1+(1+5.1×10-9p)z]}

(6a)

(6b)

接触压力与外载荷平衡：

F(t)=∬Ωp(x,y,t)dxdy

(7)

混合润滑中界面剪切力和摩擦因数计算如下：

(8)

μ=∬Ωτxdxdy/F(t)

(9)

式中：μs为干接触摩擦因数，取值0.1。

2数值求解与模型验证

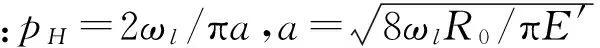
为验证模型有效性并为后续混合润滑计算提供初值，选取光滑表面模型计算并与经验公式对比。工况F=1×103N，ω1=30 rad/s，ω2=40 rad/s，对应Hertz参数pH=1.16 GPa，a=0.274 mm。

图2为有限长线接触光滑表面润滑结果，其中图2(c)～(d)分别为截面y=0和x=0润滑解。由图2知，接触线端部出现压力峰和膜厚紧缩，接触线中段区域压力与膜厚分布平缓。选取截面y=0的中心膜厚与最小膜厚，并与经验公式对比[9]，如表2。由表2可知，数值解与经验公式差异在合理范围，说明算法对有限长线接触模型是有效的。在后续有限长混合润滑计算中，粗糙度均逐步进入接触区域，且采用对应工况光滑解为迭代初值。

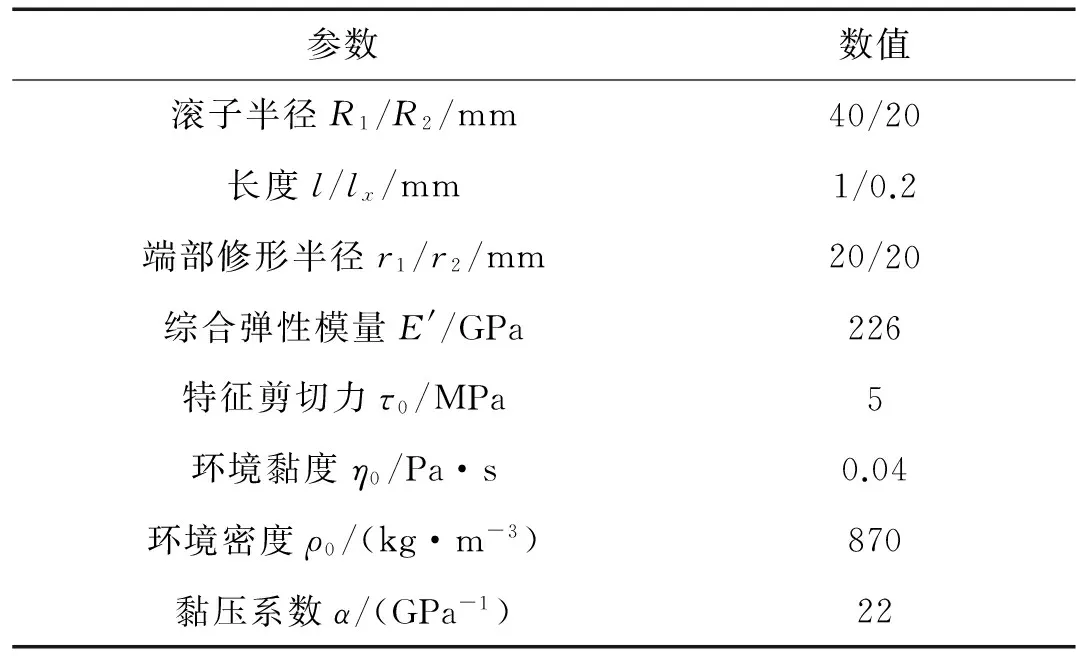
表1　接触副与润滑油性能参数

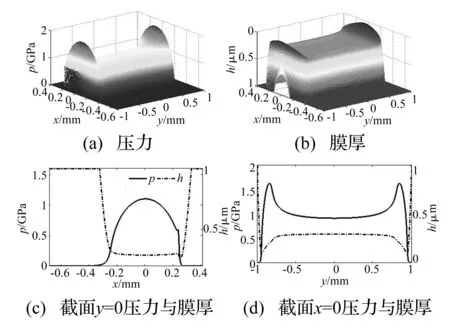
图2　有限长线接触光滑表面润滑解Fig.2 Results of smooth surface for finite line contact

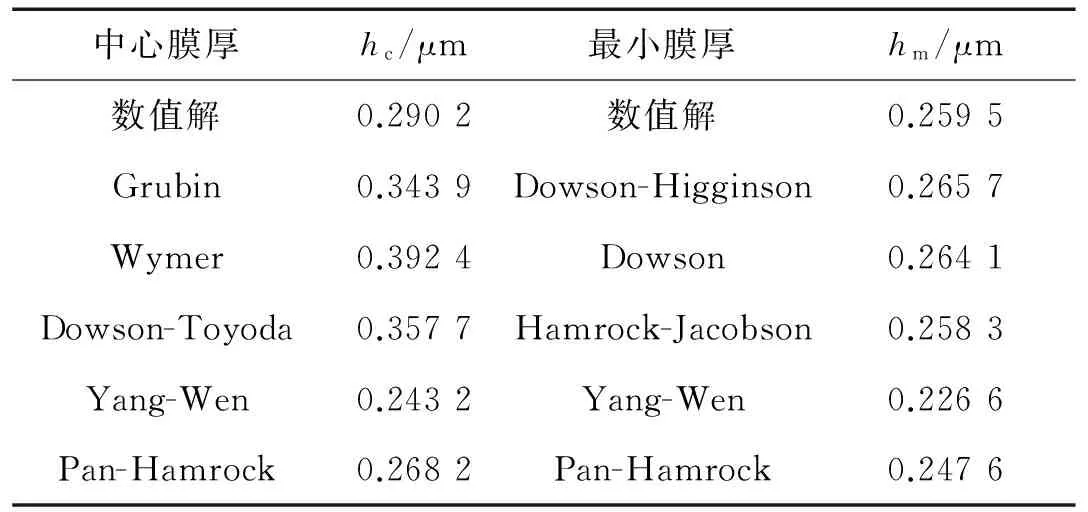
中心膜厚hc/μm最小膜厚hm/μm数值解0.2902数值解0.2595Grubin0.3439Dowson-Higginson0.2657Wymer0.3924Dowson0.2641Dowson-Toyoda0.3577Hamrock-Jacobson0.2583Yang-Wen0.2432Yang-Wen0.2266Pan-Hamrock0.2682Pan-Hamrock0.2476

3结果分析与讨论

机械加工方法形成界面精度差异较大，粗糙度波长、幅值及工况参数对接触副的润滑状态产生较大影响。选择二维规则正弦表面粗糙度函数，讨论粗糙度参数与工况变化对有限长线接触混合润滑特性影响。

3.1波长变化

选取二维粗糙度波长满足λ=λx=λy、Am=0.3 μm。讨论波长变化对有限长线接触混合润滑特性影响，如图3。由图3可知，随着粗糙度波长增大，接触线中段的干接触区域逐渐减少且压力波动幅度降低、平均膜厚升高、端部接触压力显著降低。对比光滑解，表明波长增大有益于接触副润滑。图4展示了波长变化对接触面剪切力影响，在接触线端部的剪切力明显较大，这与压力分布一致，可预测随着波长增大，接触副摩擦系数降低。

图3　波长对有限长线接触混合润滑影响Fig.3 Influence of wavelength on mixed-EHL

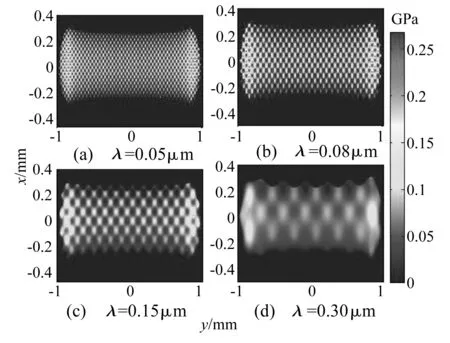
图4　波长对接触面剪切力影响Fig.4 Influence of wavelength on shear stress

3.2幅值变化

图5为幅值变化对有限长线接触混合润滑影响，其中图5(a)、(c)和图5(b)、(d)分别为截面y=0、x=0的压力与膜厚分布。由图5可知，随着粗糙度幅值增大，接触压力波动幅度增大且围绕光滑解波动，而润滑膜厚波动中心逐渐降低，当幅值增大到一定值时干接触发生。对应工况接触面剪切力如图6所示，说明剪切力变化规律与压力波动一致。

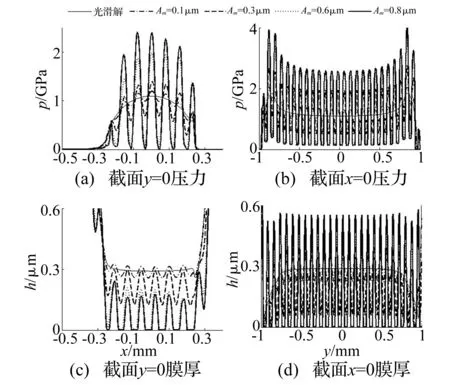
图5　幅值对有限长线接触混合润滑影响Fig.5 Influence of amplitude on mixed-EHL

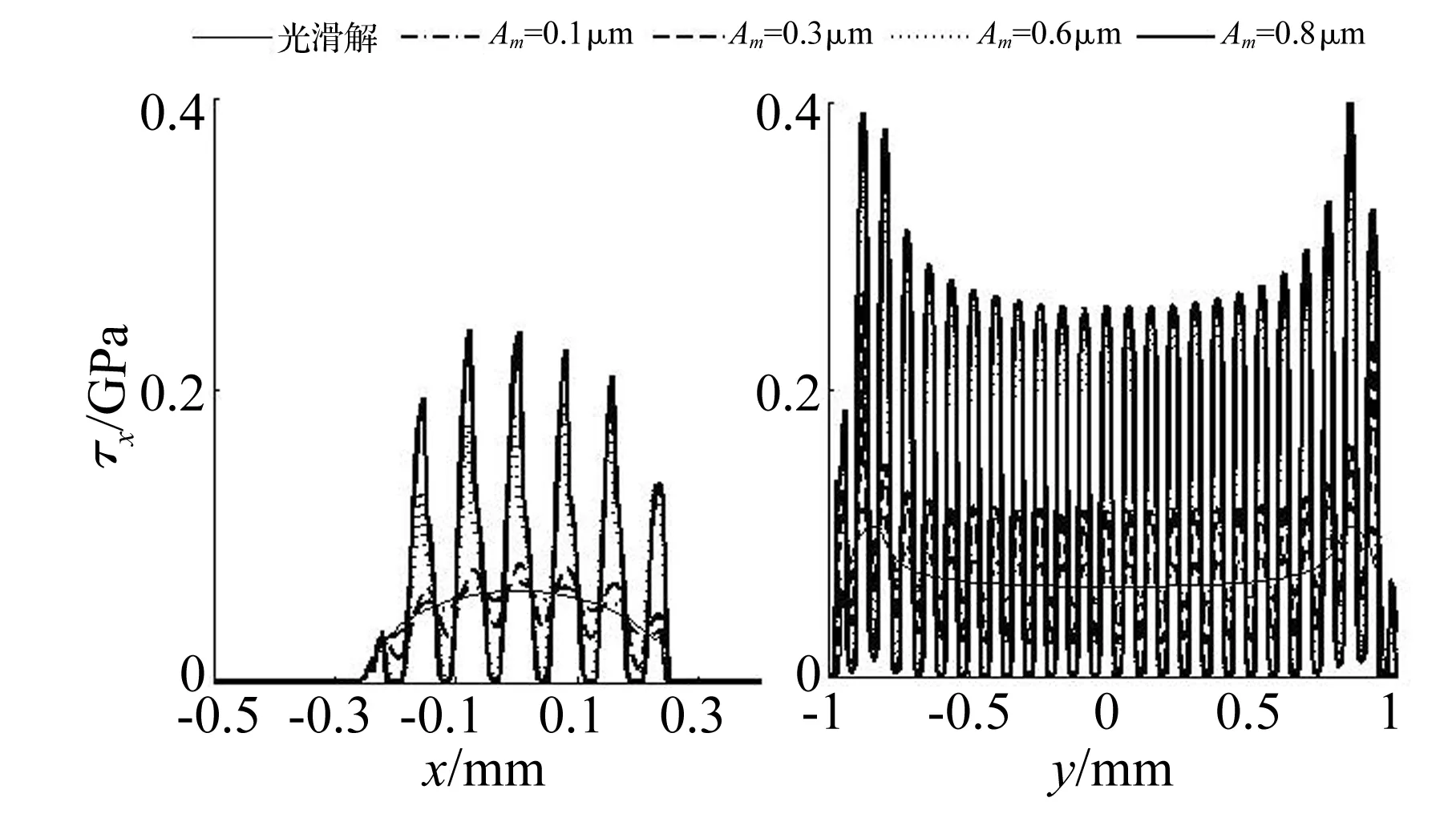
图6　幅值对接触面剪切力影响Fig.6 Influence of amplitude on shear stress

3.3工况变化

借鉴文献[13]的特征参数论述，定义有限长线接触混合润滑特征参数：平均膜厚ha、接触载荷比Rcl、接触面积比Rca、膜厚比λσ，其中特征参数计算区域为X=[-0.9,0.9]、Y=[-0.9,0.9]。选择粗糙度参数Am=0.3 μm、λ=λx=λy=0.078 mm，讨论载荷与转速变化对润滑特性影响。

图7、8为工况对有限长线接触混合润滑特性影响。无量纲参数范围为W=5.0×10-5～4.0×10-3、U=4.0×10-15～9.0×10-11，涵盖了工程接触副的大部分工况。图7说明，随着载荷增大，伴随膜厚比降低对应的摩擦因数、接触面积比和载荷比均增大；图8说明，随着转速增大，伴随膜厚比增大，对应的接触面积比与载荷比先迅速降低，然后趋于平缓，摩擦因数随转速增大先降低、然后平缓并小幅增大，具有典型‘Stribeck’曲线特征。对比图7和图8说明，在润滑状态转换区域润滑特征参数变化显著，且接触载荷比与面积比并不完全一致。

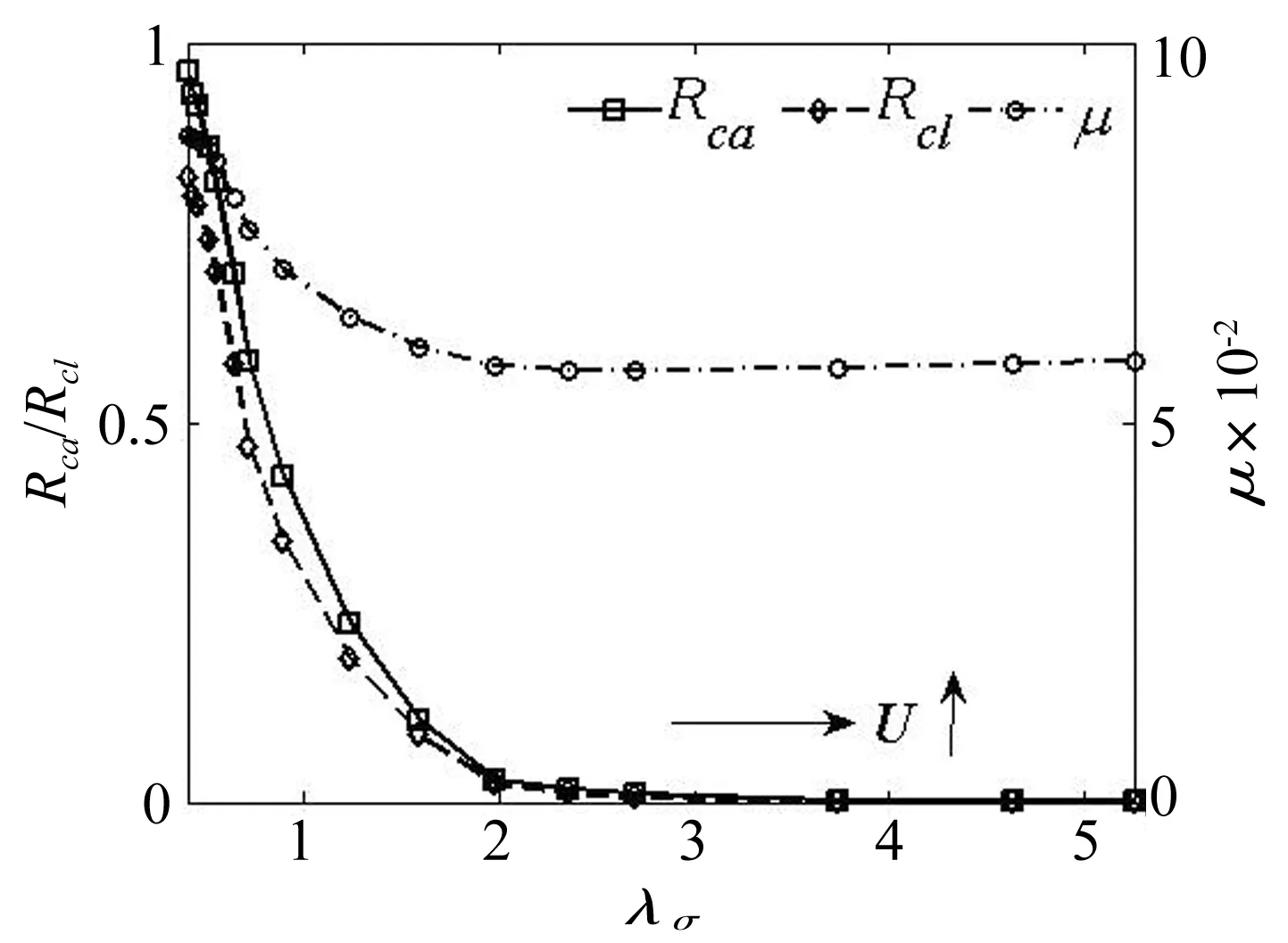
图8　转速变化变化对有限长线接触混合润滑影响Fig.8 Influence of speed on mixed lubrication of finite line contact

3.4粗糙度方位角影响

机械加工表面粗糙度纹理呈现一定的相位分布，选择x和y方向波长比λx/λy=2的正弦粗糙度表面，讨论粗糙度的方位角变化对有限长线接触混合润滑特性影响，如图9所示。

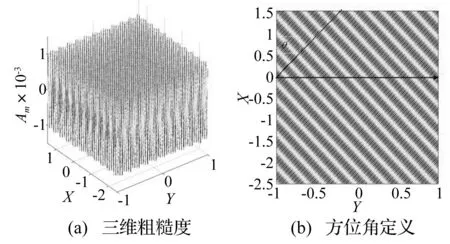
图9　粗糙度方位角示意图Fig.9 The diagram of orientation angle for roughness

图10对应无量纲工况参数W=1.657×10-4，U=1.325×10-11，Am=0.3 μm。由图10可知，随着粗糙度方位角变化，润滑特征参数均呈现周期性变化，这与几何分布对称性一致。随着方位角增大，摩擦系数、接触载荷比与面积比均先增大，然后降低，而平均膜厚则相反。结果表明，沿卷席速度方向波长较大时，有利于接触副润滑，此时粗糙度类似纵向分布。当粗糙度方位角为45°时，平均膜厚最小且接触载荷比最大。产生上述现象，是粗糙度和端部膜厚紧缩共同作用结果。对应工况的接触压力和膜厚分布如图11所示，说明互补方位角的润滑状态图呈对称分布。

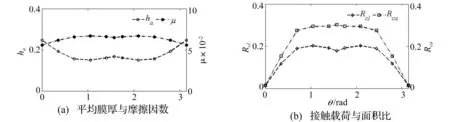
图10　粗糙度方位角对有限长线接触混合润滑特性影响Fig.10 Influence oforientation angle on mixed-EHL for finite line contact

图11　各粗糙度方位角对应有限长线接触混合润滑云图Fig.11 Contour maps of pressure, film thickness and shear stress in several orientation angles

4结论

建立了有限长线接触混合润滑模型，并讨论工况和粗糙度特征参数对润滑特性影响，获得以下结论：

(1) 随着粗糙度波长增大，接触副中段首先由混合润滑过渡到全膜润滑，且对应压力波动显著降低，说明较大的粗糙度波长有益于接触副润滑。有限长线接触存在明显的端部接触，粗糙度幅值进一步增强了端部的接触压力。随着粗糙度幅值增大，压力波动幅度更加剧烈，膜厚波动中心逐渐降低并发生局部干接触。

(2) 工程接触副的工况范围内，建立的有限长线接触混合润滑模型具有良好的适应性。随着载荷增大，摩擦系数、接触载荷比与面积比均线性增大；随着转速增大，摩擦系数呈现典型的‘Stribeck’曲线特征，润滑特征参数在混合润滑与全膜润滑转换区间变化显著，其中接触载荷比与面积比并不完全一致。

(3) 粗糙度方位角对有限长线接触混合润滑影响显著。随粗糙度方位角绕卷吸速度方向连续变化，润滑特征参数呈现周期性变化。当粗糙度长波长与卷吸速度成45°时，接触副的润滑状态最差；当粗糙度长波长与卷吸速度一致时，润滑状态最好，说明粗糙度纹理方向垂直卷吸速度时有利于有限长线接触润滑。

参 考 文 献

[1] Wang K L, Cheng H S. A numerical solution to the dynamic load, film thickness and surface temperature in spur gear, part 1 analysis [J]. ASME Journal of Mechanical Design, 1981, 103:177-187.

[2] Wang Y Q, Li H Q, Tong J W,et al. Transient thermoelastohydrodynamic lubrication analysis of an involute spur gear [J]. Tribology International,2004,37(10):773-782.

[3] Li S,Kahraman A. A transient mixed elastohydrodynamic lubrication model for spur gear pairs [J]. ASME Journal of Tribology, 2010, 132(1):1-9.

[4] Liu H J, M Ken, Zhu C C,et al. Spur gear lubrication analysis with dynamic loads [J]. Tribology Transactions, 2013, 56(1):41-48.

[5] Mostofi A, Gohar R. Elastohydrodynamic lubrication of finite line contacts [J]. ASME Journal of Tribology,1983,105(3):598-604.

[6] 徐文，马家驹，陈晓阳. 滚子摩擦弹流润滑特性及其应用Ⅰ：有限长直母线滚子的弹流数值解[J]. 摩擦学学报，1998,18(1):39-44.

XU Wen, MA Jia-ju, CHEN Xiao-yang. Elastohydrodynamic lubrication of finite line contact Ⅰ: Numerical analysis of elastohydrodynamic lubrication for finite cylindrical roller contact [J]. Tribology, 1998,18(1):39-44.

[7] Liu X L, Yang P R. Analysis of the thermal elastohydrodynamic lubrication of a finite line contact [J].Tribology International, 2002, 35:137-144.

[8] 孙浩洋，陈晓阳，杨沛然. 相交圆弧修形滚子的重载热弹流研究[J]. 机械工程学报，2004,40(7):99-104.

SUN Hao-yang, CHEN Xiao-yang, YANG Pei-ran. Thermal elastohydrodynamic lubrication of cylindrical rollers with crown profiled ends at heavy load [J]. Chinese Journal of Mechanical Engineering, 2004, 40(7):99-104.

[9] Ren N, Zhu D, Chen W W, et al. A three-dimensional deterministic model for rough surface line-contact EHL problems [J]. ASME Journal of Tribology, 2009,131(1):1-9.

[10] 华同曙，陈晓阳，丁建宁. 摆动工况下有限长线接触弹流润滑的实验研究[J]. 摩擦学学报，2010，30(6):543-547.

HUA Tong-shu, CHEN Xiao-yang, DING Jian-ning. Experimental investigation for finite line contact of elastohy-drodynamic lubrication (EHL) under oscillating motion [J]. Tribology, 2010，30(6):543-547.

[11] 陈芳华，王久根，张根源. 对数修形圆锥滚子的弹流润滑分析[J]. 机械工程学报，2011,47(19):143-148.

CHEN Fang-hua, WANG Jiu-gen, ZHANG Gen-yuan.Elastohydrodynamic lubrication of tapered roller with logarithmic profile [J]. Chinese Journal of Mechanical Engineering, 2011, 47(19):143-148.

[12] 王文中，操鸿，胡纪滨. 渐开线斜齿轮非稳态弹流润滑数值模拟研究[J]. 摩擦学学报，2011,31(6):604-609.

WANG Wen-zhong, CAO Hong, HU Ji-bin. Numerical simulation of transient elastohydrodynamic lubrication of helical gears[J]. Tribology, 2011,31(6):604-609.

[13] Zhu D, Wang J X, Ren N, et al.Mixed elastohydrodynamic lubrication in finite roller contacts involving realistic geometry and surface roughness [J]. ASME Journal of Tribology, 2012, 134(1): 011504-1-10.

[14] Mihailidis A, Agouridas K, Panagiotidis K. Non-newtonian starved thermal-elastohydrodynamic lubrication of finite line contacts [J]. Tribology Transactions, 2013, 56(1):88-100.

基金项目：国家自然科学基金(51405142);湖北省自然科学基金(2014CFB583)资助

收稿日期：2015-04-09修改稿收到日期：2015-07-27

中图分类号:TH117

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.14.015

Analysis on the mixed lubrication performance of finite line contact

LIU Ming-yong1, LIU Huai-ju2, ZHU Cai-chao2, WANG Lei1

(1. Hubei Agricultural Machinery Engineering Research and Design Institute, Hubei University of Technology, Wuhan 430068, China；2. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China)

Abstract:The mixed elastohydrodynamic lubrication (mixed-EHL) of finite line contact was studied, considering the regular surface roughness. The effects of the wavelength, amplitude and orientation angle of surface roughness and the working conditions variation on lubrication characteristics were discussed. The results show that the numerical model is simple and robust. The lubrication state at the middle of contact line is the first to be changed when the wavelength goes up. The increase in roughness amplitude increases the pressure fluctuation and hence enhances the edge effect. The working conditions have obvious influence on the lubrication state. Within the region of lubrication state transition, the characteristic parameters change significantly. The effect of roughness orientation angle on mixed lubrication is significant. The orientation angle of 0 degree is advantageous to finite line mixed-EHL, and that of 45 degree is the worst.

Key words:finite line contact; mixed-EHL; roughness; orientation angle

第一作者 刘明勇 男，博士，讲师，1985年9月生